Design of Heusler Precipitation Strengthened NiTi- and PdTi-Base SMAs for Cyclic Performance

Abstract

For a wide range of actuation applications, the performance of NiTi-based shape memory alloys is limited by cyclic instability associated with accommodation slip. For medical applications, low-Ni compositions are also desirable. Increasing yield strength via precipitation of a coherent nanoscale Ni₂TiAl-type Heusler phase from a supersaturated B2 matrix is an effective approach for eliminating slip in order to improve the stability of the functional response and increase the structural fatigue life. Quaternary additions that partition into the L2₁ Heusler phase, such as Zr or Pd, are favorable for reducing interphase misfit and maintaining coherency during aging. Phase relations and precipitation kinetics in quaternary Ni(TiZrAl), low-Ni (PdNi)(TiAl), and Ni-free (PdFe)(TiAl) systems are summarized from TEM and atom probe tomography data in the literature. Strengthening behavior during isothermal aging is compared in the NiTiZrAl and PdNiTiAl systems, and recent work characterizing a high-strength, low-Ni “Hybrid” (PdNi)(TiZrAl) alloy is presented. A systems design approach is taken in which an optimal microstructure for peak strengthening is identified while other property objectives such as transformation temperature, misfit, radiopacity, and biocompatibility are satisfied.

Introduction

Motivation and Background

Due to their unique thermomechanical properties, shape memory alloys (SMAs) are utilized across a vast array of industries including biomedical, aerospace, automotive, and civil applications. Near-equiatomic NiTi (or Nitinol) is one of the most widely used commercial SMAs. Large reversible strains associated with thermal recovery along with the highly compliant superelastic loading response makes NiTi-based SMAs ideal candidates for expandable transcatheter devices such as vascular stents and artificial heart valve frames. SMAs are also utilized as actuators in automotive and aerospace applications because of their high power density and simple actuation mechanism, which allow for quiet, compact, and efficient actuator design.

In all of these applications, operational conditions include thermal and/or mechanical cyclic loading, often into the high or ultra-high cycle fatigue (HCF/UHCF) regimes. Therefore, in the parametric design of materials for these applications we must focus on fatigue life as a key property objective in ensuring safe and reliable device performance. Increasing the yield strength of the austenite phase, σ _y, is important for improving both structural and functional fatigue resistance. Increasing σ _y (1) decreases the accumulation of plastic strain at stress raisers such as non-metallic inclusions or other defects (2) promotes deformation via reversible processes such as the thermoelastic martensitic transformation, and (3) helps minimize the buildup of accommodation slip at the austenite/martensite interface during phase transformation that can lead to instability and/or irreversibility during thermal or mechanical cycling. While cold working materials can lead to high-strength levels, it has been shown to degrade the superelastic response due to interference with interface movement during transformation [1]. Therefore, utilizing a strengthening dispersion of coherent, nanoscale precipitates to increase the yield strength of the austenite phase is a promising method of improving fatigue life while maintaining cyclic stability. Controlled precipitation of an L2₁ (Ni₂TiAl-type) Heusler phase in a supersaturated B2 Ni(Ti,Al) matrix can be achieved by aging at intermediate temperatures (500–800 °C). Characterization of phase relations and kinetics of aging in this 2-phase field is critical for designing processing parameters to achieve an optimized microstructure. Current progress in this regard is outlined in the “Process Optimization” section of this paper.

The NiTi/Ni₂TiAl system is analogous to the gamma/gamma′ NiAl/Ni₂TiAl system that has been studied extensively in the context of Ni superalloy development. Only recently has interest been developed in the NiTi/Ni₂TiAl system for precipitation strengthened SMAs. This paper will focus on the recent research developments surrounding phase relations, precipitation and coarsening kinetics, phase stability, and strengthening behavior of the ternary Ni₅₀(Ti,Al)₅₀ system as well as selected higher-order quaternary and quinary systems of interest.

One system that has been studied is the Ni₅₀(Ti,Zr,Al)₅₀ system, which utilizes Zr addition for both its excellent solid solution strengthening capabilities and its beneficial effect on decreasing interphase lattice misfit. Based on ab initio calculations and experimental measurements, Zr has been found to preferentially inhabit Ti sites in the B2 and L2₁ phases [2]. The ternary NiTi/Ni₂TiAl system has a relatively large lattice misfit of −2.57 %, which can cause loss of coherency during aging and is detrimental to precipitation strengthening. The larger Zr atoms partition preferentially into the Heusler phase, thus helping minimize interphase misfit. NiTi-based systems such as the NiTiZrAl system are of interest for automotive applications, where cost is a limiting factor and additions of precious metals such as Pd and Pt, as discussed in the following section, are prohibitive. A detailed review of this system will be discussed in the “Ni(Ti,Zr,Al) System” section.

When designing SMA systems for biomedical applications, biocompatibility is an important property objective to address. In individuals with Ni hypersensitivity, systemic allergic reactions to NiTi-based devices can cause inflammation near the implant and eventual device failure [3]. Biocompatibility concerns thus drive the development of low-Ni and Ni-free alternatives to conventional NiTi-base SMAs. Preliminary cytology studies by Bender et al. indicate that a low-Ni Pd₃₀Ni₂₀Ti₄₆Al₄ alloy shows improved cell viability over binary NiTi when live cell count was measured after exposure to metal alloy powders dispersed in growth media [4]. Additionally, Pd-base alloys have increased radiopacity compared to binary NiTi allowing for better X-ray visibility of devices during placement procedures. The same low-Ni alloy studied by Bender et al. exhibited a 141.9 % radiopacity improvement over binary NiTi [4]. Therefore, the low-Ni and Ni-free PdTi-base systems show good promise for biomedical applications.

The PdTi system has been widely studied as a high-temperature SMA [5, 6]. Hosoda et al. found that ternary additions of 3d transition metals on the Pd sublattice can effectively stabilize the austenite phase down to room temperature or body temperature range, allowing for design of superelastic biomedical alloys [7]. As with Zr, Pd has a larger atomic volume than Ni and partitions to the Heusler phase, decreasing interphase misfit. An extensive characterization of transformation behavior and precipitation in low-Ni (Pd,Ni)₅₀(Ti,Al)₅₀ and Ni-free (Pd,Fe)₅₀(Ti,Al)₅₀ system is reviewed in the “PdTi-Base System” section of this paper.

Despite being of interest in many high-temperature actuator applications, binary PdTi SMAs demonstrate poor recoverable strain due to their low critical slip stress. Pd is a significant solution softener, and slip stress of the parent B2 phase decreases by more than 75 % in Ni_49.5−x Pd _x Ti_50.5 as Pd is increased from 15 to 46 at.% [8]. Zirconium is of interest as an effective strengthening addition in the PdTi system, much like in the NiTi system. Kawakita et al. note significant solid solution strengthening effects from the addition of 5 % Zr, resulting in increased martensite yield strength, austenite transformation stress, and recoverable strain during compression [9]. Models used to describe strengthening in these materials are outlined in the “Strengthening Models” section, while application of these models to prototype NiTiZrAl and PdNiTiAl systems is addressed in the “Calibrating Strength Models” section.

The preliminary investigation of the “hybrid” (Pd,Ni)₅₀(Ti,Zr,Al)₅₀ system is also presented, which combines the biocompatibility of PdTi-base systems with the strengthening of Zr and the benefits of coherent Heusler precipitation to achieve a high-strength, fatigue-resistant, low-Ni SMA design. New data regarding phase relations and strengthening behavior in a non-transforming (A _f ≪ RT) alloy (Pd₃₀Ni₂₀Ti₃₈Zr₈Al₄ nominal) is characterized via atom probe tomography (APT) and Vickers microhardness. From APT data, average particle radius and phase composition can be measured. Using these measurements as model inputs, other material parameters such as phase fraction, interphase misfit, austenite finish temperature (A _f), and solid solution strengthening can be calculated, as described in “Models” section.

Lastly, a brief overview of non-metallic inclusions in commercial NiTi is included in “Non-metallic inclusions” section. Non-metallic inclusions such as micron-scale Ti₄Ni₂O _x -type oxides and Ti(C,O)-type carbides form due to oxygen and carbon impurities introduced during commercial melt processes. They can act as potent fatigue crack nucleation sites and are therefore important to address when considering the fatigue life of NiTi-based components. Both empirical and computational approaches have been taken to understand the role non-metallic inclusions play in fatigue life. Recent advances in industrial processing technologies are also discussed.

Design Objectives

In an effective materials design, it is imperative to understand and define design objectives. These objectives will vary based on the application of interest. The operational temperature (T _op) and desired thermomechanical response for a given application will determine the optimal transformation temperature for an alloy. In the case of actuator applications such as SMA springs, valves, or switches, the application might require switching between two constrained/biased strain states (one-way shape memory effect) or two unconstrained/unbiased trained shapes (two-way shape memory effect) upon temperature cycling. Therefore in these applications the designed alloy must have M _f > T _low and A _f < T _high as well as minimal hysteresis. For applications which undergo mechanical loading in which a superelastic (SE) response is desired, the alloy should be austenitic at T _op, thus the design objective for transformation temperature is A _f < T _op. For SE biomedical applications such as vascular stents and artificial heart valve frames, A _f is targeted to be between 10 and 15 °C, sufficiently below body temperature to ensure a superelastic response during operation.

In both SE and shape memory applications, resistance to functional fatigue is critical for maintaining a stable cyclic response. Maximizing the yield strength of the B2 phase is important for improving both functional and structural fatigue resistance. The required yield strength goals will be determined by the specific application device design and loading conditions.

Minimizing interphase misfit is important for maximizing driving force for precipitation to increase fine-scale particle number density. Additionally, large coherency strains can be an obstacle for martensite interface motion during phase transformation, increasing interfacial frictional work and transformation hysteresis [10], which is detrimental to actuator applications with narrow temperature ranges. Lastly, early coherency loss during particle growth and coarsening would prohibit dislocation cutting and cause premature bypass, leading to non-optimal peak strength values [11]. For these reasons, the objective is set to reduce lattice misfit from δ = −2.57 % in the NiTiAl system to |δ| < 1 % in quaternary and higher-order system designs.

Cost is also an important design factor. For automotive applications, use of precious metals such as Pd or Pt may be prohibitive, while the cost-to-benefit ratio may be acceptable in aerospace or medical applications. A cost analysis of stent devices indicated that while replacing a binary NiTi alloy with a low-Ni Pd₃₀Ni₂₀Ti₄₆Al₄ alloy would increase the cost of raw materials by a factor of 3.7; the raw materials make up just a small portion of the device cost to hospitals, resulting in a projected device cost increase of only 8 % [12]. This cost increase might be outweighed by the benefit that a biocompatible PdTi-based device would provide to a severely Ni-hypersensitive patient with no treatment alternative.

In biomedical applications, biocompatibility and radiopacity must be considered. Cell cytology studies can be used to investigate relative cytotoxicity of different alloys, while attention must also be paid to surface finish and corrosion behavior. Additionally, the material for medical devices must be radiopaque, or visible under an X-ray fluoroscope, in order to aid device insertion and maintenance. Radiopacity may be quantified by calculating X-ray absorption as a function of composition as described in the “Radiopacity model” section. The absorption of binary NiTi is considered the baseline and improvement over this level is desirable.

Systems Design of SMAs

Design Chart

The systems design chart provides a useful way to illustrate and elucidate the complex interrelationships between processing, structure, properties, and performance in a material system [13]. This chart emphasizes the reciprocity of the relationships as well as the hierarchical nature of the microstructural subsystems. An example of a systems design chart for precipitation strengthened SMAs can be found in Fig. 1.

Fig. 1

Systems design chart for a high-performance precipitation strengthened SMA

Developing computational and analytical models to describe the relationships between subsystem boxes, denoted with connector lines, allows for parametric design of high-performance materials. While a scientific analysis might focus on a smaller number of subsystems, understanding the interrelationships between each subsystem is crucial for a systems-based design.

Models

Strengthening Models

Yield strength can be considered a simple linear superposition of base strength (incorporating Hall–Petch strengthening at a constant grain size), solid solution strengthening, and precipitation strengthening contributions (Eq. 1). Solid solution strengthening may be modeled using a sum of elemental strengthening or softening coefficients k _i multiplied by the mole fraction of the added component x _i raised to an empirical power coefficient 1/n _i (n _i  = 1,2,…), as shown in Eq. 2. Strengthening and power coefficients used in this paper can be found in Table 1.

Table 1 Fitted empirical solid solution strengthening constants and exponents for substitutional additions to NiTi

Precipitation strengthening contributions can be described by the classic shearing/looping interaction of a dislocation with precipitates in a matrix. At small particle sizes, a dislocation shearing mechanism dominates, in which it is energetically favorable for a dislocation to cut through a precipitate. Due to modulus, ordering, coherency, and antiphase boundary (APB) contributions, shearing resistance increases as a function of particle size and can be combined into a prefactor K1 with a dependence on r ⁿ where n = 1 for these systems (Eq. 3). At larger particle sizes and interparticle spacing distances, dislocation looping becomes the dominant interaction mechanism, in which dislocations bypass incoherent particles in a matrix and strengthening decreases as 1/r (Eq. 4). Shearing behavior, i.e., the magnitude of the prefactor K1, is dependent on precipitate composition, while looping behavior, i.e., the value of K2, is independent of precipitate composition.

$$\sigma_{\text{tot}} = \sigma_{\text{base}} + \Delta \sigma_{\text{ss}} + \Delta \sigma_{\text{ppt}}$$

(1)

$$\Delta \sigma_{\text{ss}} = \mathop \sum \limits_{i = 1}^{n} k_{i} x_{i}^{{\frac{1}{{n_{i} }}}}$$

(2)

$$\Delta \sigma_{\text{ppt}}^{\text{shear}} = K1 \cdot f^{\frac{1}{2}} \cdot r^{n}$$

(3)

$$\Delta \sigma_{\text{ppt}}^{\text{loop}} = K2 \cdot f^{\frac{1}{2}} \cdot \frac{1}{r}.$$

(4)

When experimental data are normalized by $f^{\frac{1}{2}}$ and the precipitation strengthening values are plotted versus the average particle radius, curves for Eqs. 3 and 4 can be fit to the data and the analytically determined intersection corresponds to the peak-strengthened state and optimum particle radius.

Kinetic Models

Lacking a completed kinetic database to provide a detailed calculation of phase diagrams (CALPHAD)-based computational model for particle growth trajectory as a function of aging time and temperature, the next best estimation is to determine rate constants for prototype systems as a function of aging time. Thus a clear processing/properties relationship can be modeled allowing the prediction of average particle radius and design of optimum processing method. For systems under high supersaturation it has been shown that nucleation is rapid and growth is suppressed [14], such that a simple Lifshitz–Slyozov–Wagner (LSW)-type coarsening model might adequately describe average particle size evolution as directly related to t ^1/3 through a rate constant, k, in the pure coarsening regime [15].

$$\bar{r}^{3} - \bar{r}_{0}^{3} = kt$$

(5)

Here $\bar{r}$ is the average particle size at time t and $\bar{r}_{0}$ is the average radius at the onset of coarsening. For highly supersaturated systems in which precipitation is rapid and growth is suppressed, $\bar{r}_{0}$ can be approximated as r ^*, the critical radius for precipitation [14]. Jung et al. found that microstructural dynamics in NiTiZrAl-base systems were governed by particle growth at 800 °C but by coarsening at 600 °C, which is consistent with the increased supersaturation of the matrix at lower aging temperatures [2].

Composition Trajectory Models

For supersaturated systems under evolving unstable equilibrium, phase composition can be modeled as a function of particle radius following Gibb–Thomson trajectories for dilute solutions with the following relation:

$$C_{i}^{r} = Ae^{\frac{b}{r}},$$

(6)

where $C_{i}^{r}$ is the composition of component i in the phase of interest at radius r, and A and b are fitted constants where A corresponds to $C_{i}^{r = \infty }$, or the equilibrium solubility of component i the modeled phase. Fitting experimental data for phase composition and radius at selected aging conditions allows for parametric prediction of non-equilibrium phase relations at finite particle sizes, and also allows for extrapolation to r = ∞ to determine equilibrium solubilities.

Misfit Model

The unconstrained interphase misfit (in percent) between the B2 matrix phase and L2₁ precipitate phase is calculated by the relation

$$\delta = \left( {\frac{{a_{{{\text{L}}2_{1} }} - 2a_{{{\text{B}}2}} }}{{2a_{{{\text{B}}2}} }}} \right) \times 100$$

(7)

For the ternary NiTiAl system, the lattice parameter for the B2 phase $a_{\text{B2}} = a_{\text{NiTi}} = 0.3010\, {\text{nm}}$ and the lattice parameter for the L2₁ phase $a_{{{\text{L2}}_{1} }} = a_{{{\text{Ni}}_{ 2} {\text{TiAl}}}} = 0.5865 \,{\text{nm}}$ are known and the misfit can be calculated to be −2.57 %. For higher-order systems, the composition-dependent lattice parameters may be calculated using a weighted sum of the known atomic volumes of the constituents in the B2 and L2₁ phases and the misfit can be calculated from the cube root of the ratio of the average atomic volume for each phase:

$$\delta = \left( {\sqrt[3]{{\frac{{\bar{\Omega }_{{{\text{L2}}_{1} }} }}{{\bar{\Omega }_{{{\text{B}}2}} }}}} - 1} \right) \times 100$$

(8)

$$\bar{\Omega }_{{{\text{L}}2_{1} }} = \sum\limits_{i = 1}^{n} {x_{i} \Omega_{i}^{{{\text{L}}2_{1} }} }$$

(9)

$$\bar{\Omega }_{{{\text{B}}2}} = \sum\limits_{i = 1}^{n} {x_{i} \Omega_{i}^{{{\text{B}}2}} }$$

(10)

Jung utilized literature values along with X-ray diffraction data performed on experimental alloys to determine the average atomic volumes of Ni, Ti, Al, Zr, Hf, Pd, and Pt in the B2 and L2₁ phases [2]. Atomic volume was derived based on lattice spacing by utilizing a simplifying assumption that atomic volume is not dependent on the lattice site that an atom occupies. The values calculated by Jung are found in Table 2.

Table 2 Measured and calculated atomic volumes at 25 °C for atomic species in the B2 and L2₁ phases [2]

A _f Model

The austenite finish temperature, A _f, can be approximated as T ₀ for superelastic polycrystals [16] and modeled as a function of B2 composition using a Redlich–Kister polynomial for a 2-sublattice system. This model is analogous to the substitutional regular solution model used in solution thermodynamics with a Redlich–Kister power series model for higher-order excess free energy contributions [17]. The 2-sublattice Redlich–Kister model for A _f temperature is given in Eq. 11 for compounds (A ₁,…,A _p )^I(B ₁,…,B _q )^II with sublattices I and II and elemental site fractions given by y ^m _i for species A _i or B _i on sublattice m (m = I or II, respectively). The parameter A _f(i:j) is the binary regular solution endpoint, corresponding to the A _f temperature of binary compound A _i B _j . The higher-order terms ^v L (v = 0,…,2) represent the ternary interaction parameters which describe interactions between two species j and k on one sublattice in the presence of a third species i on the neighboring sublattice. The temperature-dependent term from solution thermodynamics is ignored.

$$A_{\text{f}} = \mathop \sum \limits_{i = 1}^{p} \sum\limits_{j = 1}^{q} {y_{i}^{\text{I}} y_{j}^{\text{II}} A_{{{\text{f}}(i:j)}} } + \mathop \sum \limits_{i = 1}^{p} \mathop \sum \limits_{j = 1}^{q} \sum\limits_{k \ne j}^{q} {y_{i}^{\text{I}} y_{j}^{\text{II}} y_{k}^{\text{II}} {}^{v}L_{(i:j,k)} \left( {y_{j}^{\text{II}} - y_{k}^{\text{II}} } \right)^{v} } + \mathop \sum \limits_{i = 1}^{q} \mathop \sum \limits_{j = 1}^{p} \sum\limits_{k \ne j}^{p} {y_{i}^{\text{II}} y_{j}^{\text{I}} y_{k}^{\text{I}} {}^{v}L_{(j,k:i)} \left( {y_{j}^{I} - y_{k}^{I} } \right)^{v} } .$$

(11)

Higher-order interaction parameters ^v L as well as some binary endpoints A _f(i:j) which cannot be determined empirically must be fit to experimental data by minimizing the residual sum of squares. This fitting process is analogous to the process used for creating thermodynamic databases for CALPHAD techniques based on experimental data. A _f can be determined experimentally by differential scanning calorimetry (DSC) or differential thermal analysis (DTA) methods.

Data for many binary and ternary systems can be found in the literature. Hosoda et al. summarized experimental M _s data for 3d transition metal additions in ternary Pd_(50−y)X _y Ti₅₀ systems for X = Cr, Mn, Fe, Co, and Ni and found the B2 stabilizing effect to be significant and linear with respect to at.% addition and constant with respect to electron-to-atom (e/a) ratio, approximately 900 K/(e/a). Selected data from Hosoda et al. is shown in Fig. 2 for ternary additions of Ni, Co, and Fe, which result in decreases in M _s temperature of −14.2, −25.5, and −36.2 °C/at.%, respectively.

Fig. 2

M _s temperature dependence on ternary additions X = Ni, Co, Fe in a Pd₍₅₀−_y)X_yTi₅₀ alloy, from experimental data compiled in [7]

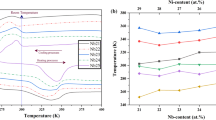
While prominent transformation peaks in Ti-rich Ni(Ti,Zr) have been observed in alloys with up to 25 at.% Zr [18], only limited data on the effect of ternary additions of Zr in PdTi has been reported. Kawakita et al. observed that in Pd(Ti,Zr) alloys, DSC peaks are prominent for 5 at.% Zr additions on the Ti sublattice, while at 10 at.% Zr the peaks become smaller and broader, and multiple peaks are exhibited upon cooling. In NiTi, Zr additions have a stabilizing effect on the martensite, while in PdTi systems Zr is found to decrease the transformation temperature (Fig. 3).

Fig. 3

A _f temperature as a function of Zr content in the Ni₅₀Ti_(50-x)Zr_x [18] and Pd₅₀Ti_(50-x)Zr_x [9] systems. Dotted lines indicate the predicted A_f temperatures in these ternary systems based on the Redlich–Kister A_f model with interaction parameters fitted to both data from the literature plotted here and experimental data

Radiopacity Model

The radiopacity, or extent to which a material can be seen in an X-ray fluoroscope, is quantified at a given X-ray energy by calculating the X-ray absorption, $1 - \frac{I}{{I_{0} }},$ where I is the intensity of the transmitted X-ray and I ₀ is the intensity of the incident X-ray. X-ray absorption is given by

$$1 - \frac{I}{{I_{0} }} = e^{{ - \left( {\frac{\mu }{\rho }} \right)\rho x}},$$

(12)

where x is the strut thickness, ρ is the alloy density, and $\left( {\frac{\mu }{\rho }} \right)$ is the mass attenuation given by

$$\left( {\frac{\mu }{\rho }} \right) = \mathop \sum \limits_{i} w_{i} \left( {\frac{\mu }{\rho }} \right)_{i},$$

(13)

where w _i is the mass fraction of component i and $\left( {\frac{\mu }{\rho }} \right)_{i}$ is the mass attenuation coefficient of the component i at the X-ray energy of interest, which for many medical X-ray fluoroscope applications is 30 keV. Radiopacity can be considered as the radiopacity improvement (RI) over binary NiTi, which has an X-ray absorption at 30 keV of 0.1863 or 18.6 % for a part with a standard stent thickness of x = 40 μm [12].

Experimental Methods

Details regarding experimental procedures used in studying the NiTiAl-X, low-Ni, and Ni-free quaternary systems can be found in the literature [12, 19–21]. The “hybrid” alloys presented in “Low-Ni Hybrid (Pd,Ni)(Ti,Zr,Al)” section were arc melted in Ar using >99 % purity stock material and homogenized at 950 °C for 24 h. Samples were then cut into slices for mechanical, thermal, and structural characterization using an Accutom precision saw. Aging treatments were performed at various times at temperatures between 500 and 600 °C. All samples were encapsulated in evacuated quartz tubes with Ta foil getters to avoid surface oxidation and water quenched after each heat treatment.

Atom probe tomography (APT) was used to measure phase compositions and precipitate size after aging in a non-transforming Pd₃₀Ni₂₀Ti₃₈Zr₈Al₄ “hybrid” alloy prototype. For the isothermal study, samples were aged at 600 °C for 0.25, 1, 3, 5, 10, and 100 h. For the isochronal study, samples were aged for 3 h at 500, 530, and 600 °C. APT was performed on an imago local electrode atom probe (LEAP) at 80 K with a pulse frequency of 250 kHz and a laser energy of 20–30 pJ. Data analysis was performed using IVAS 6.3.2 software. Average precipitate radius and phase compositions were measured using proximity histograms (proxigrams) around Al isoconcentration surfaces representing the L2₁/B2 interface.

Vickers microhardness was used to characterize mechanical properties of the non-transforming “hybrid” sample as well as the peak-aged superelastic Ni-free Pd_42.2Fe_7.8Ti₄₄Al₆ alloy. Hardness tests were performed with 1000 g indent force/10 s dwell time and 20 indents per sample. For the precipitation hardening study, room temperature Vickers hardness was performed on hybrid alloy samples aged at 500 °C for 3, 5, 10, 24, and 50 and 360 h. Hot hardness measurements utilized a resistive ceramic heating stage in atmosphere and were performed on the PdFeTiAl alloy at T = 25, 40, 60, 80, 100, 125, 145, and 190 °C.

To measure M _s, M _f, A _s, and A _f temperatures in transforming alloys, differential scanning calorimetry (DSC) was performed using a Mettler Toledo DSC822 differential scanning calorimeter with a ramp rate of 10 °C/min for heating.

Process Optimization

To design effective aging treatments in order to obtain an optimized microstructure, it is imperative to develop descriptions of both particle growth kinetics and phase composition trajectory. In this section, experimental data for precipitate size and phase composition at various aging times and temperatures are used to fit the models described in “Kinetic Models” and “Composition Trajectory Models” sections. Data from numerous prototype systems are collected and presented here, with the ultimate goal of facilitating the development of a thermodynamic database to predict phase relations in the multicomponent alloy system.

In addition to designing a peak-aged microstructure, much work has been done focusing on issues related to homogenization and the presence of metastable Ni-rich phases and Ti-rich intermetallics. Additionally, in Zr-containing systems the formation of brittle or low-melting phases that can cause workability or incipient melting issues must be addressed. Identification of appropriate solution and hot working temperatures to avoid these issues are discussed in “Ni(Ti,Zr,Al) System” section.

NiTi-Base Systems

NiTiAl-X (X = 5 at.% Pd, Pt, Zr, Hf) Systems

Early investigation by Jung [2, 19] of quaternary NiTiAl-X (X = Pd, Pt, Zr, Hf) systems examined elemental partitioning in highly overaged samples in order to evaluate the best candidate for reducing misfit. Early prototypes included small quaternary additions (5 at.%) of Pd and Pt on the Ni sublattice as well as Zr and Hf on the Ti sublattice, with 4–5 at.% Al on the Ti sublattice. A ternary alloy with 5 at.% Al was also studied. Average particle size was measured using centered dark field TEM imaging of samples aged at 600 and 800 °C for 100 and 1000 h. Phase compositions and partitioning coefficients were measured using AEM on highly overaged samples aged at 800 °C, and APT was used to measure phase relations in samples aged at 600 °C due to small precipitate sizes.

It was found that coarsening kinetics are retarded in the Zr- and Hf-containing systems when compared to particle growth in the ternary NiTiAl system, while the Pd- and Pt-containing systems had relatively faster kinetics. Therefore, the ternary, 5Zr, and 5Hf samples were aged for 1000 h while the 5Pd and 5Pt samples were aged for 100 h. After aging at 800 °C, the 5Zr alloy exhibited an average particle radius of 233 ± 81.3 nm but after aging at 600 °C the average particle size was only 5.65 ± 1.00 nm. Due to the extremely fast kinetics at 800, 600 °C was chosen as a more appropriate aging temperature to achieve a finely dispersed array of nanoscale precipitates.

A coherent 〈100〉-oriented cuboidal microstructure with r _avg = 6.7 nm was seen in the Pt-containing system aged at 600 °C, but full coherency loss was observed at r _avg = 96.8 nm after aging at 800 °C. Coherency is observed in the Zr, Hf, and Pd systems after 600 °C aging treatments (r _avg = 5.65, 6.24, and 9.48 nm respectively), although precipitates in the Zr and Hf systems are cuboidal while the Pd system maintains spherical precipitates. Irregular and/or cuboidal semicoherent morphologies were observed in the Zr and Hf systems with average radii of 233 and 312 nm after aging at 800 °C, while precipitates in the Pd-containing system remained fully spherical indicating full coherency and very low misfit at an average radius of 34.6 nm. An additional 20Pd alloy studied exhibited fully coherent precipitates with an average radius as large as 75.5 nm after aging at 800 °C.

Key learnings from this initial research into quaternary NiTiAl-X systems were that while partitioning behavior is temperature dependent for Zr, Hf, and Pt, partitioning of Pd remained nearly constant across temperatures and compositions. Pt tends to strongly partition into the B2 matrix, making it an unfit candidate for low-misfit quaternary systems. Measured values for partitioning coefficients are summarized in Table 3.

Table 3 Experimentally measured partitioning coefficients X = Pd, Pt, Zr, and Hf in the NiTiAl-X system

Zr was shown to be more effective at decreasing misfit than Hf at 600 °C, and was therefore chosen for further investigation for strengthening studies for low-cost automotive applications. A preliminary Ni₅₀Ti₃₂Zr₁₅Al₃ prototype aged for 100 h at 600 °C demonstrated extremely effective strengthening with a yield strength of 2.1 GPa during compression at 180 °C. Further investigation into the precipitation behavior and strengthening in the NiTiZrAl system will be reviewed in “Ni(Ti,Zr,Al) system” and “Calibrating strength models” sections, respectively.

Pt-containing samples cannot be electropolished for APT sample preparation, making LEAP analysis for Pt-containing alloys prohibitive. Additionally, partitioning behavior of Pt at both 600 and 800 °C was detrimental to interphase misfit. Therefore, Pd was determined to be the most promising candidate for developing low-Ni biomedical alloys.

Ni(Ti,Zr,Al) System

Despite demonstrating excellent strengthening capabilities, the phase relations and processing issues involved with designing Zr-containing alloys must be further understood. There are a number of processing challenges that must be considered with Zr-containing alloy designs. Alloys with as low as 3 at.% Zr have shown brittleness in hot working processes due to the formation of the NiTiZr laves phase and (Ti,Zr)₂Ni intermetallic [21]. Hsieh and Wu showed that in Ni₅₀Ti_(50−x)Zr _x systems for x ≥ 10 at.%, brittle (Ti,Zr)₂Ni and NiTiZr were in equilibrium with the matrix after homogenizing at 900 °C [22].

Three scaled-up 5-lb NiTiZrAl prototypes were investigated by Bender in [12]: Ni₅₀Ti₃₂Zr₁₅Al₃, Ni₅₀Ti₃₈Zr₈Al₄, and Ni₅₀Ti_35.8Zr_8.7Al_5.5. The first two fractured during hot rolling at 950 °C, and the third was homogenized at 950 °C and then shattered during hot rolling at 825 °C. SEM/EDS investigation indicated the presence of both a NiTiZr laves phase and an metastable Ni-rich Ni₃(Ti,Zr)₂ T-phase in equilibrium with the B2 matrix. Scheil modeling was employed to investigate non-equilibrium cooling and the resulting effects on incipient melting at homogenization or hot working temperatures. In the three alloys listed above, liquid was predicted to be present down to 899, 961, and 894 °C, respectively, indicating that the first and third buttons probably experienced some melting during homogenization and/or hot rolling. In Fig. 4, the non-equilibrium cooling solidus lines are plotted for various Zr and Al compositions. In order to fully avoid incipient melting with compositions up to 5 at.%Al and 20 at.%Zr, both annealing and hot working temperatures must be limited to 850 °C. In addition it is clear that the C14 (laves) phase is stabilized at high Zr content levels, which decreases with added Al; the maximum Zr content limit as a function of Al composition should be carefully considered to avoid formation of the brittle laves phase.

Fig. 4

Scheil simulations showing solidus as a function of Zr content for various Al contents. The square symbols indicate the composition at which the phases are in equilibrium with liquid at the solidus temperature shift from single-phase B2 to two-phase B2 + L2₁. The triangle indicates the Zr content above which the NiTiZr laves phase (C14) is present in equilibrium with liquid, B2, and L2₁. Figure reproduced with permission from [12]

With care taken toward avoiding incipient melting and formation of brittle intermetallic phases, Zr-based alloys show promise in reducing interphase misfit in low-cost NiTi-base designs for automotive applications. Atom probe tomography was performed on Ni₅₀Ti₃₈Zr₈Al₄ aged at 600 °C. Particle size evolution can be seen to follow a t ^1/3 trend consistent with LSW-type coarsening behavior Fig. 5. The rate constant is smaller than in the ternary system, as Jung observed in his initial TEM analysis of overaged systems. Fitted Gibbs–Thomson constants for composition trajectory are presented in Tables 4 and 5 and are plotted in Fig. 6a. The critical radius for nucleation, r _crit, can be identified by extrapolating the matrix composition trajectory to the bulk composition. The scaling of the x-axes in Fig. 6 have been adjusted to reflect the limits of $\left( {\frac{1}{{r_{\infty } }},\frac{1}{{r_{\text{crit}} }}} \right)$.

Fig. 5

Particle size trajectory versus aging time at 600 °C. Dotted lines represent fitted t ^1/3 curves consistent with LSW-type coarsening. Experimental data are based on LEAP measurements of phase composition in four experimental prototypes: Ni₅₀Ti₃₈Zr₈Al₄ [12], Pd_(30–36)Ni_(14–20)Ti_(45–46)Al_(4–5) [12], Pd_42.2Fe_7.8Ti₄₄Al₆ [21], and Pd₃₀Ni₂₀Ti₃₈Zr₈Al₄

Table 4 Values for fitted constant A (at.%) from Gibbs–Thomson trajectory for phase composition fitted to experimental LEAP data

Table 5 Values for fitted constant b (nm) from Gibbs–Thomson trajectory for phase composition fitted to experimental LEAP data

Fig. 6

Gibbs–Thomson plots for composition trajectory versus 1/r. Atomic composition of elemental components in the B2 phase (a,c,e,g) and L21 phase (b,d,f,h) is plotted versus the inverse of the measured average radius for various aging treatments, along with fitted Gibbs–Thomson curves (solid lines) for (a, b) Ni₅₀Ti₃₈Zr₈Al₄ at 600 °C [12], (c, d) Pd₂₀Ni₃₀Ti₄₆Al₄ at 550 °C [20], (e, f) Pd_42.2Fe_7.8Ti₄₄Al₆ at 600 °C [21], and (g, h) Pd₃₀Ni₂₀Ti₃₈Zr₈Al₄ at 600 °C. The x-axis is scaled such that x _max = 1/r ^*, i.e., corresponding to the critical radius for nucleation

APT reconstructions for the 15Zr3Al and 8Zr4Al systems aged at 600 °C for long times (100+ h) as well as 5Zr5Al starting even at shorter aging times (10 h) show the presence of a lenticular metastable Ni-rich Ni₄Ti₃ intermetallic phase which is not apparent in TEM micrographs at 800 °C [12]. It should be noted when describing phase relations for these alloys during aging at 600 °C that they do not reflect a B2 + L2₁ 2-phase field.

PdTi-Base Systems

Low-Ni (Pd,Ni)(Ti,Al) System

A range of low-Ni prototypes have been investigated by Bender and Jiang using APT at 600 °C [12] and 550 °C [20]. At 600 °C the investigated systems had compositions in the range of Pd_30–36Ni_14–20Ti_45–46Al₄. At 550 °C a non-transforming Pd₂₀Ni₃₀Ti₄₆Al₄ prototype was characterized, the results of which were utilized in calibrating a strengthening model in “Calibrating Strength Models” section. The precipitate growth trajectory at 600 °C is plotted in Fig. 5 along with other systems characterized at that aging temperature. The kinetics are faster than in the NiTiZrAl system, consistent with TEM observations for the first quaternary prototypes presented in “NiTi-Base Systems” section. The measured rate constants for systems aged at 600 °C can be found in Table 6.

Table 6 Rate constants for systems characterized at 600 °C

Partitioning behavior during aging at 550 °C can be observed in the Gibbs–Thomson trajectories in Fig. 6, from which equilibrium solubility can be determined. From the proxigram in Fig. 7b, it is clear that in the PdNiTiAl system, Pd partitions into the L2₁ while Ni partitions into the B2 phase. A pseudoternary phase diagram in Fig. 8 shows tie lines for equilibrium solubilities at 600 °C based on the extrapolated Gibbs–Thomson trajectories for the NiTiZrAl, PdNiTiAl, and PdNiTiZrAl systems.

Fig. 7

Pd₃₀Ni₂₀Ti₄₆Al₄ alloy peak aged at 530 °C for 15 h. a IVAS reconstruction of APT data. Heusler phase is visualized using 12 %Al isoconcentration surfaces. b Proxigram around B2/L2₁ interface shows compositional profiles. Data from [20]

Fig. 8

Pseudoternary phase diagram for NiTiZrAl (squares), PdNiTiAl (diamonds), and PdNiTiZrAl (triangles). Tie lines represent equilibrium solubilities calculated from LEAP data for samples aged at 600 °C

A secondary microscale interdendritic phase was observed in most low-Ni microstructures after homogenization. This phase has a Ti-rich Ti₂(Ni,Pd)-type composition and is thought to be a proto-oxide similar to the Ti₄Ni₂O _x oxides seen in commercial arc-melted NiTi [23]. Jiang conducted a solution treatment study in which a 950 °C 20 h homogenization was followed by 100 h solution treatments at 900, 950, 1000, and 1050 °C [20]. Solution treatments led to spheroidization and a slight reduction in phase fraction of the Ti-rich secondary phase, but full dissolution of the phase was not observed. The Ti₂Ni phase has been shown to be brittle in NiTi so attention must be paid to this phase despite the relatively low phase fraction and large interparticle spacing.

Ni-Free (Pd,Fe)(Ti,Al) System

A Ni-free Pd_42.2Fe_7.8Ti₄₄Al₆ prototype was aged at 600 °C and investigated using APT [21]. Pd partitioning was not observed to be as strong as in low-Ni alloys because Ni was not present on the Pd sublattice in competition for B2 sites. Fe partitioned strongly out of the Heusler phase, with an equilibrium composition of only 1.70 at.% in L2₁. Al solubility in the B2 phase is greatly increased compared to low-Ni, with an equilibrium solubility value of 3.85 %. Early prototypes with 4 at.% Al bulk compositions showed negligible precipitation due to lack of supersaturation. From Fig. 5 it is clear that the coarsening kinetics are faster than in the NiTiZrAl system but slower than in the low-Ni PdNiTiAl system.

Structure/Property Relations

Calibrating Strength Models

Hardness data were collected on non-transforming Ni₅₀Ti₃₈Zr₈Al₄ aged at 600 °C [12] and Pd₂₀ Ni₃₀Ti₄₆Al₄ aged at 550 °C [20] for various times. An empirical power law fit to experimental data from [24] relating hardness to yield strength in NiTiAl alloys was used to estimate yield strength values from Vickers hardness numbers.

Using Eq. 1 to isolate the precipitation strengthening contribution and normalizing by f ^1/2 based on phase fraction values measured by APT, the strengthening data from both systems can be plotted together (Fig. 9). The dashed lines represent the shearing curves (Eq. 3) fit to the NiTiZrAl and PdNiTiAl data for r ≤ r _opt, for which K1 was calculated to be 1419.1 and 491.3 MPa/nm, respectively. The much lower value for K1 in the Pd-containing system is most likely due to modulus softening of Pd in contrast to the modulus strengthening of Zr. The modulus hardening effect proves to be the most significant contributor to shear resistance, and the relationship between L2₁ composition and resulting K1 value, or shear resistance, can be quantified.

Fig. 9

Strengthening data from non-transforming Ni₅₀Ti₃₈Zr₈Al₄ aged at 600 °C [12] and Ni₃₀Pd₂₀Ti₄₆Al₄ aged at 550 °C [20]. The dashed and dot-dashed lines represent the shearing curves (Eq. 3) fit to the NiTiZrAl and NiPdTiAl data for r ≤ r _opt, respectively. The dotted line is the looping curve (Eq. 4) fit to both sets of experimental data for r > r _opt

The dotted line is the looping curve (Eq. 4) fit to both sets of experimental data for r > r _opt (K2 = 3089.4 MPa-nm). Due to the different shear resistance values, each alloy has a different resulting value for r _opt. For the NiTiZrAl system, 1.5 nm is found to be the optimum particle size, corresponding to a 10 h 600 °C aging treatment. In the low-Ni PdNiTiAl alloy, peak strengthening occurs at r _opt = 2.5 nm. Previous curve fitting that constrained the value of n in Eq. 3 to 0.5 resulted in an optimum radius value of 2.3, but a fit with n = 1 was found to describe the behavior of these systems more accurately. The PdNiTiAl alloy exhibited a peak strength of 1.05 GPa with misfit value of −0.77 % and radiopacity improvement (RI) of 129 %, while the NiTiZrAl alloy exhibited a peak strength of 2.40 GPa, misfit of −0.67 %, and RI of 35.6 %.

Transformation Temperature

A_f values have been measured using DSC for a number of ternary and higher-order systems of interest here. Data for the ternary (Ni,Pd)Ti were reported by Linquist and Wayman as reproduced in [25], from which values for the Ni:Ti and Pd:Ti binary regular solution endpoints A _f(Ni:Ti) and A _f(Pd:Ti) as well as higher-order ⁰L and ¹L terms describing the ternary (Ni,Pd)Ti interaction can be calculated. As shown in Fig. 2, ternary data in (Pd,X)Ti systems have been studied by Hosoda et al. [7], including (Pd,Fe)Ti. Transformation temperatures in the Ni(Ti,Zr) (Zr = 0–20 at.%) system was characterized by Hsieh and Wu [18], while limited data for the Pd(Ti,Zr) (Zr = 0, 5, 10 at.%) have been reported by Kawakita et al. [9]. Literature data with fitted Ni(Ti,Zr) and Pd(Ti,Zr) interaction parameters are plotted in Fig. 3.

Experimental data were collected on the quaternary low-Ni PdNiTiAl system [12, 20]. While none of the Ni(Ti,Zr,Al) alloys characterized by Jung and Bender proved to be transformable, by switching Al to the Ni sublattice, transforming alloys can be designed. Data have been collected for transforming (Ni,Al)(Ti,Zr) prototypes [20], allowing for the calculation of Al:Ti, Al:Zr, and higher-order (Ni,Al):Ti parameters. In combination with the data from the Ni-free (Pd,Fe)(Ti,Al) system presented in “Ni-Free (Pd,Fe)(Ti,Al) System” section, Fe:Ti and Fe:Al interaction parameters as well as higher-order (Pd,Fe):Ti have been calculated. The calculated interaction parameters are summarized in Tables 7 and 8. Contour plots containing A _f predictions using aforementioned fitted constants are calculated for four quaternary systems of interest: low-Ni PdNiTiAl, Ni-free PdFeTiAl, hybrid PdNiTiZr, and transforming NiAlTiZr (Fig. 10). The bold lines represent the contours at 10 and 15 °C, and the plotted points represent experimental data points used in fitting. Experimentally measured A _f values can be found in a supplementary table A1.

Table 7 Calculated interaction parameters for binary solution endpoints A _f(i:j) where i is the component on sublattice I and j is the component on sublattice II

Table 8 Calculated ternary interaction parameters for the 0th (⁰ L)- and 1st (¹ L)-order interactions

Fig. 10

Contour plots for A _f based on the fitted Redlich–Kister polynomial model for A _f temperatures. Bold contour lines correspond to A _f = 10 and 15 °C. Dots represent experimental data points used in the model fitting. Experimental A _f values can be found in supplementary table A1

The parabolic shape of the ternary (Ni:Pd)Ti interaction in which the A _f temperature first decreases upon addition of Pd on the Ni sublattice and then increases with increasing Pd content (as seen in Fig. 11) is a result of the Pd stabilizing a B19 martensite instead of the B19′ martensite that is observed in binary NiTi systems. The ternary system could also be modeled by two linear models that have separate B2 → B19′ and B2 → B19 regular solution endpoints for the two different martensites stabilized in that system. These endpoints are found to be $A_{{f({\text{Ni:Ti}})}}^{{{\text{B}}19}} = - 240.0$ and $A_{{f({\text{Pd:Ti}})}}^{{{\text{B}}19^{\prime}}} = - 410.8$. Figure 11 plots experimental data points for A _f values in the (Ni,Pd)Ti system from Linquist and Wayman as reported in [25] along with the discrete B19 and B19′ expressions (dashed lines) and continuous Redlich–Kister function (solid line) for the prediction of A _f temperature. It is clear that the Redlich–Kister function with higher-order parameters merely approximates the discrete function made up of two intersecting linear trends, leading to possible overestimations of A _f in the 10–15 at.% Pd compositional region.

Fig. 11

A _f temperature in Ni_50−x Pd _x Ti₅₀ for x = 0–50 at.%. Solid diamonds represent data from Linquist & Wayman as reported in [25]. The solid line represents the continuous Redlich–Kister function for predicting A _f, while the dotted lines represent the linear functions for B2→B19′ (circles) and B2→B19 (squares)

Cyclic Stability Validation

Validation of cyclic stability performed on a transforming Pd₃₀Ni₂₀Ti₄₆Al₄ alloy aged at 600 °C for 5 h showed stable behavior in the DSC after 30 thermal cycles as well as good cyclic stability under compression cycles and reversible transformation strains up to 4 % [12]. However, when compared to samples aged at 550 and 530 °C, the best cyclic stability was found in samples aged at 530 °C [20]. The increased stability at lower-temperature aging treatments is most likely due to an increased driving force for precipitation resulting in a finer dispersion of nanoscale precipitates with a larger number density. Jiang found that the temperature dependence of the rate constant in PdNiTiAl followed an Arrhenius trend, and used this to design a peak-strengthened alloy aged at 530 °C for 15 h. LEAP analysis of this peak-strengthened alloy shows precipitates with an average size of 2.76 nm, close to the targeted value of 2.5 nm. An A _f of approximately 20 °C was measured and cyclic compression performed at T = 36 °C showed superelastic loops exhibiting high cyclic stability and a recoverable superelastic strain of 5.5 %.

An optimum heat treatment for the Ni-free Pd_42.2Fe_7.8Ti₄₄Al₆ of 3.5 h at 600 °C was designed to target an r _opt = 2.5 nm based on the strengthening study in the low-Ni system [21]. LEAP analysis on a peak-aged alloy measured an average precipitate radius of 2.3 nm. The radiopacity improvement is calculated to be 217.2 %. The A _f temperature of 52.3 °C was measured using DSC, which shifted by only 0.1 °C over 10 heating/cooling cycles. Cyclic compression showed stable loading behavior and recoverable strains on the order of 3 %. Hardness values measured at T = 145 °C (T = M ^σ_s ) indicate a B2 yield strength of 423 MPa. The diminished strength of the Ni-free prototype is due to the solution and modulus softening effect of Pd. Cyclic stability is achieved despite relatively low strength due to the reduced transformation strain of the B2 → B19 transition such that lower strength levels are necessary to prevent accommodation slip. The addition of Zr in the “hybrid” design described in “Low-Ni Hybrid (Pd,Ni)(Ti,Zr,Al)” section will attempt to mitigate this strength loss and prevent accommodation slip in low-Ni B19′ stabilized systems with larger transformation strains.

Low-Ni Hybrid (Pd,Ni)(Ti,Zr,Al)

Precipitation in a “hybrid” Pd₃₀Ni₂₀Ti₃₈Zr₈Al₄ prototype was characterized at 600 °C using APT. Phase composition trajectories can be observed in Fig. 6. Ni and Pd partitioning trends are similar to low-Ni systems, while Zr partitions to the L2₁ phase as in the NiTiZrAl system. Misfit values were calculated to be −0.02 % after 100 h of aging, lower than any previously studied system. Kinetics at 600 °C in the hybrid system were found to be much faster than in any of the previously characterized systems (Fig. 5). For this reason, precipitation kinetics were also investigated at 530 and 500 °C, and 500 °C was determined to have sufficiently reduced kinetics such that a nanoscale precipitation study could be performed. Hardness measurements were performed on samples aged at 500 °C for various times, and peak strengthening was observed to occur at 50 h (Fig. 12). Peak strength was measured to be 550.8 VHN corresponding to an estimated yield strength of 1.8 GPa. This strength level is 70 % higher than that observed in a low-Ni Pd₂₀Ni₃₀Ti₄₆Al₄ peak-aged system, demonstrating that even with higher Pd content, strength can still be improved significantly with relatively small Zr additions. However, at temperatures at or below 530 °C, a slightly Ni-group rich (Pd,Ni) _x (Ti,Zr) metastable compound is found to be present in addition to the L2₁ phase. This third phase is Zr-rich and the compound stoichiometry deviates from Ni-rich Ni₄Ti₃ metastable intermetallic compounds commonly observed in binary NiTi as well as some NiTiZrAl alloys [12, 19]. Characterizing this third phase is important in analyzing the strengthening contributions of precipitation in this alloy system at 500 °C and is the subject of continuing investigation.

Fig. 12

Vickers microhardness versus aging time in Pd₃₀Ni₂₀Ti₃₈Zr₈Al₄ aged at 500 °C

To design a transforming hybrid alloy, prototypes needed to be made to fit interaction parameters in the hybrid system for the A _f model. Three transforming hybrid prototypes were fabricated: Pd₅₀Ti₄₁Zr₅Al₄, Pd₅₀Ti₃₉Zr₅Al₄, and Pd₄₅Ni₅Ti₄₁Zr₅Al₄. In combination with data on the ternary PdTiZr system from [9], the A _f model was extended to include the (Pd,Ni)(Ti,Zr,Al) design space. A _f predictions based on this model can be observed in Fig. 10c. Due to the limited, high-temperature data points used in fitting this model, its reliability in predicting A _f at lower temperatures is not optimized. More experimental data must be collected for transforming systems in the temperature region of interest to extend the reliability of the model for designing a superelastic hybrid alloy.

Non-metallic Inclusions

In commercial NiTi melting techniques such as vacuum induction melting (VIM), vacuum arc remelting (VAR), and some combination of these processes (VIM/VAR), non-metallic inclusion particles form during solidification due to C and O impurities introduced into the melt by source materials or the melt process itself. Both Ti(C,O)-type carbides or Ti₄Ni₂O _x -type oxide phases can form, the phase fractions of which are dependent upon the impurity concentration levels [23]. Due to their brittle properties and incoherency with the surrounding matrix, inclusions can break up during cold drawing processes, forming long stringers of fractured particles in the order of 10–50 μm in length (Fig. 13). The fractured inclusions can partially delaminate from the surrounding matrix forming sharp crack tips or voids which act as potent fatigue crack nucleation sites. In order to characterize behavior in the UHCF regime, it is critical to be able to model the morphology, distribution, and potency of these fatigue nucleants.

Fig. 13

Oxide and carbide inclusions in a cold-drawn NiTi tube. Broken and elongated stringers occur in the drawing direction (horizontal)

Moore has utilized image-based meshes of a NiTi material with a realistic inclusion stringer to predict fatigue limit using Finite Element Analysis [26]. Employing crystal plasticity models, a fatigue indication parameter (FIP) was calculated at various applied strain amplitudes which can be correlated to Coffin–Manson type fatigue behavior [27]. The FIP values were calibrated to the minimum fatigue life calculated from experimental NiTi diamond element fatigue data. The minimum (P = 0) fatigue life, i.e., fatigue limit, was calculated by fitting normalized experimental data to a 3-parameter Weibull function as per the method outlined in [28]. The effect of matrix strength on the fatigue life was quantified using this technique. A 50 % increase in NiTi yield strength over a base strength of 750 MPa resulted in a 44 % increase in fatigue limit at 10⁹ cycles, increasing from 0.27 to 0.39 % strain amplitude (Fig. 14).

Fig. 14

Plot for applied strain amplitude versus minimum fatigue life (N _f,min) for a NiTi matrix with an inclusion stringer. Curves show fatigue limit for NiTi with typical B2 yield strength values (filled) and a NiTi matrix with 50 % enhanced B2 yield strength values (unfilled). The dashed arrow indicates the resultant increase in fatigue limit at 10⁹ cycles. Results are based on calibrated FIP values computed from FEA simulations on an image-based mesh as reported in [26]

A number of studies have attempted to quantify the effects of inclusion type and morphology on fatigue performance. Current consensus in the literature is that in high and ultra-high cycle fatigue, the maximum inclusion size is a critical factor in determining fatigue behavior [29–31]. Launey et al. found that in a direct comparison between standard VAR material and high purity (HP) VAR material with reduced maximum inclusion size and area fraction, the HP VAR material exhibited a fatigue limit at 10⁷ cycles five times higher than that of the standard VAR material [29]. Rahim et al. found that in bending rotation tests, HP material with a low volume fraction of oxides and extremely low volume fraction of carbides outperforms both oxide- and carbide-heavy samples in low cycle fatigue (LCF), while in the HCF and UHCF regimes fatigue performance in carbide-heavy samples outperformed both oxide-heavy and HP samples [30]. This behavior was due to the fact that oxides form stringers both at a higher rate and of larger sizes than carbides during thermomechanical processing. Recent developments by G. Rau GmbH (Pforzheim, Germany) demonstrate the use of electron beam refining (EBR) techniques to reduce the maximum inclusion size. Compared to conventional VAR material, VAR samples treated with EBR showed a reduction in maximum inclusion size from >15 to 1.1 μm and area fraction from 0.73 to 0.06 %, corresponding to an increase in fatigue strain limit at 10⁷ cycles from 0.6 to 1.3 % (personal communication from A. Pelton to D. Frankel). Process modifications such as EBR which reduce the nucleation potency of non-metallic inclusions are integral in addressing fatigue concerns in commercial NiTi. Calculations are underway to predict the fatigue performance potential of combining the inclusion size reduction with L2₁ nanodispersion strengthening.

Conclusions and Recommendations

L2₁ aluminide Heusler phase precipitation and strengthening behavior in NiTiZrAl, low-Ni PdNiTiAl, Ni-free PdFeTiAl, and hybrid PdNiTiZrAl have been characterized such that kinetic, thermodynamic, and strengthening models can be fit to experimental data and utilized in a parametric alloy design to achieve stated application-dependent property objectives. Zr and Pd are employed as quaternary alloying additions that reduce interphase misfit and help maintain coherency. Particle evolution is found to be dominated by particle coarsening at 500–600 °C and LSW-type t ^1/3 rate constants can be used to predict particle size as a function of aging time. Compositional trajectories can be fit to Gibbs–Thomson equations allowing for prediction of phase composition at non-equilibrium (i.e., finite r) stages, enabling phase relations at peak strength to be determined. Additionally, Gibbs–Thomson trajectories can be used to calculate both equilibrium solubilities and the critical radius for nucleation.

A high-strength NiTiZrAl system for automotive actuator applications exhibited peak strengths of 2.40 GPa at an optimum precipitate radius of 1.5 nm. Lower peak strengths were achieved in the low-Ni PdNiTiAl system due to Pd softening. A peak strength of 1.05 GPa at r _opt = 2.5 nm was observed in a non-transforming PdNiTiAl alloy aged at 550 °C. A peak-strengthened superelastic PdNiTiAl alloy aged at 530 °C for 15 h exhibited excellent thermal and mechanical cyclic stability with reversible strains of 5.5 % in compression. A superelastic Ni-free peak-aged alloy exhibited high thermal cyclic stability despite low strength values due to reduced transformation strain. However, low-Ni and Ni-free alloys exhibited significant improvements in radiopacity over binary NiTi, which is advantageous for biomedical applications. Low-Ni “hybrid” PdNiTiZrAl alloys demonstrate the capacity for combining high strength and biocompatibility, along with extremely low misfit and improved radiopacity. A non-transforming hybrid alloy aged at 500 °C for 50 h demonstrated a peak strength level of 1.8 GPa. Further development of an A _f model based on empirical data is necessary to achieve a superelastic design for biomedical applications.

Issues due to the presence of secondary intermetallic phases, low-melting phases, and large non-metallic inclusions were addressed as important aspects of process design. A Ti-rich interdendritic phase is observed to form during the melt process in low-Ni and Ni-free systems. Lenticular Ni₄Ti₃-type metastable intermetallic phases can be seen in many Zr-containing systems aged at or below 600 °C. Non-equilibrium solidification simulations predict that a low-melting NiTiZr laves phase may limit homogenization and hot working temperatures due to incipient melting concerns. Additionally, non-metallic phases such as oxides and carbides must be considered when addressing structural fatigue life in the UHCF regime. Advanced powder metallurgy techniques such as rapid solidification and thermal spray could be explored as fabrication routes to bypass solidification pathways that lead to the formation of undesirable secondary phases.

The development of these L2₁ precipitation strengthened SMA systems provides exciting avenues for future investigation. Most current methods for strengthening NiTi-base alloys rely on the use of cold working techniques. Utilizing work-free aging treatments to produce strengthening dispersions opens the door for many net shape fabrication techniques. With the rapid advances being made in the field of additive manufacturing, the ability to produce a device via 3D printing would afford radically new processing routes and provide an alternative to traditional cold drawing and laser cutting techniques, which can result in damaging inclusion stringers.

Moving forward, there is much work to be done in expanding the current thermodynamic and kinetic databases for Pd-containing systems so that computational CALPHAD methods can be fully utilized in the systems design of these alloys. The Redlich–Kister-based A _f model can be integrated into the thermodynamic database for prediction of transformation temperature. Capillary energy adjustments based on experimental APT data can be calibrated to allow for the calculation of peak-aged non-equilibrium phase relations using ThermoCalc software. A complete database of mobility coefficients would allow for detailed DICTRA modeling of the homogenization and aging processes. With a CALPHAD framework in place, the fully parametric design of an optimized microstructure can be implemented.