Introduction

Since its inception, human race has encountered and battled deadly epidemics and pandemics due to mass infection caused by viruses, for example SARS, HIV, AIDS, H5N1,, Chicken pox and Small pox, etc. Modelling and analysis of such epidemic behavior has been an integral part of research in the areas of Biological and Physical Sciences [1,2,3,4,5]. Though the\(SIS\), \(SIR\) or \(SIRS\) models [6, 7] have been employed to study illness transmission, the incubation time has been thought to be insignificant. Hence, a new kind of model called \(SEIR\) was introduced. Similar other factors may influence the population dynamics of certain infectious diseases. Vaccination is one such component that plays a important role in the prevention and control of such illnesses. In 2006, Gumel, McCluskey and Watmough [8] considered an \(SVEIR\) model to discuss the significance of an anti \(SARS\) vaccine, where V accounts for the vaccinated population. In 2016, Wang et.al [9] studied the stability of an \(SVEIR\) model. However, both the studies and many others, were guided by integral order differential operators of the dynamical variables. In this communication we have considered Caputo order fractional derivatives of a four compartmentalized population with vaccination.

At present times an extensive investigation [10,11,12,13,14,15,16,17,18,19,20,21,22,23] of the spread of the highly contagious Coronavirus disease with alarming fatality rate is being carried out. Different models exist in epidemiology to forecast and explain the complexities of an epidemic. Kermack and Mckendrick developed one such epidemic model in 1927 [28]. Tang et al. [16] proposed a compartmental deterministic model that took illness progression, patient epidemiological status, and prevention approaches into account. The \(SIR\) model is most widely used for analyzing and forecasting disease progression adopted in 1991 by Anderson et.al [29]. However, all these models were based on integral order derivatives.

Differential equations using fractional differential operators have been found to be useful in depicting epidemic scenarios for a variety of infectious diseases [26,27,28,29,30]. Several approaches for generating precise and approximate solutions to fractional order differential equations have been developed as a result of extensive research [31,32,33,34]. Several fractional operators have been devised to explore the dynamics of epidemic systems, including Caputo–Fabrizio, Riemann–Liouville, Caputo, Hadamard, Atangana–Baleanu, Katugampola, and others. We employed the Caputo operator to examine the dynamics of COVID-19, since it has a nonlocal and nonsingular exponential kernel [35,36,37,38,39,40]. The dynamical and nonstandard computational study of a heroin epidemic model is discussed by Raza et al. [41]. For more related publications, see Refs. [42,43,44,45,46,47,48,49,50,51].

As stated earlier, vaccination is a crucial method for eradicating infectious diseases. Covid-19 vaccination has recently been confirmed as a successful method of preventing the spread of the disease. Theoretical findings indicate that the covid-19 vaccination approach differs from traditional vaccination methods in terms of achieving disease eradication at low vaccination doses. India started administering COVID-19 vaccines on January 16, 2021. 170,153,432 doses have been administered in this country as of 10 May 2021 [52, 53]. Covishield (a Serum Institute of India-manufactured version of the Oxford–AstraZeneca vaccine) and Covaxin, which were utilised in India at the start of the programme, are now licenced vaccinations (developed by Bharat Biotech). In April 2021, Sputnik V has been licenced as a third vaccination, with delivery beginning in late May 2021.

The objective of the current work is:

  1. 1.

    The model's dynamical behavior and stability are investigated.

  2. 2.

    The Basic Reproduction Number and Equilibrium Points are calculated.

  3. 3.

    Numerical simulation to confirm the results and regulate the spread of COVID-19.

  4. 4.

    In India, the model was validated and discussed in the COVID-19 instances.

The manuscript is structured as follows: Sect. 2 discusses a mathematical model with a fractional order derivative. Section 3 is devoted to the discussion of stability analysis and stability criterion of the Model. For the \(SEIR\) model with vaccination parameter, we use the Adam-Bashforth-Moulton scheme in Sect. 4. The numerical simulation and discussion are given in Sect. 5 using MATLAB. The conclusion of the paper is presented in Sect. 6.

Formulation

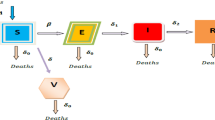
At time \(t \ge 0\), the whole population \((N)\) is divided into four classes, namely, the susceptible \((S)\), the exposed \((E)\), the infected \((I)\) and the recovered \((R)\) class. Thus

$$N(t)=S(t)+E(t)+I(t)+R(t)$$
(2.1)

The \(SEIR\) model with integer order [54, 55] is expressed as follows:

$$\begin{aligned}{D}_{t} S(t) & = \lambda - \beta SI - \mu S-\eta S, \\{D}_{t} E(t)& = \beta SI -( \mu + k ) E, \\{D}_{t} I (t)& = kE -\left( \mu + \gamma \right)I, \\{D}_{t} R\left(t\right) &= \gamma I - \mu R+\eta S, \end{aligned}$$
(2.2)

where \(\lambda \): birth rate of susceptible individuals, \(\beta \): contact rate from \(S\) to \(E\), \(\mu \): death rate, η: vaccination rate, \(k\): progression rate exposed to infected, \(\gamma \): recovery rate.

Let us go through some fundamental definitions of Caputo fractional operators [35, 56,57,58,59] for dynamical analysis.

Definition 1

The Caputo integral of the function \(g : {\mathbb{R}}^{+}\to {\mathbb{R}}\) is defined by

$${}^{C}{I}_{t}^{\alpha }\left(g\left(t\right)\right)=\frac{1}{\Gamma \left(\alpha \right)}\underset{0}{\overset{t}{\int }}(t-x{)}^{\alpha -1} g\left(x\right)dx, $$
(2.3)

where \(\Gamma ( . )\) denotes the Gamma function and \(0 < {\alpha }\le 1\) shows the fractional order parameter.

Definition 2

The Caputo derivative with order \(0<{\alpha }\le 1\) is defined by

$${}^{C}{D}_{t}^{\alpha } \left(g \left(t\right)\right)={I}^{n-\alpha }{D}_{t}^{\alpha }\left(g \left(t\right)\right)=\frac{1}{\Gamma \left(n- \alpha \right)}\underset{0}{\overset{t}{\int }}(t-x{)}^{n-\alpha -1}\frac{{d}^{n}}{d{x}^{n}} g \left(x\right)dx, $$
(2.4)

where \(n-1< \alpha <n\).

Definition 3

Let \(g\in C\left[a,b\right]\) with \(a<b,\) and \(0<{\alpha }\le 1.\) The fractional derivative in Caputo type is defined by

$${}^{C}{D}_{t}^{\alpha }\left(g\left(t\right)\right)=\frac{M( \alpha )}{(1- \alpha )}\underset{a}{\overset{t}{\int }}{g}^{{{\prime}}}\left(p\right)exp \left(-\frac{\alpha (t-p)}{1-\alpha }\right)dp,$$
(2.5)

where \(M\left(\alpha \right)\) represents the normalization function with \(M\left(0\right)=M\left(1\right)=1\).

Definition 4

Let \({}^{C}{D}_{t}^{\alpha } \left(g\left(t\right)\right)\) be a piecewise continuous on \(\left[{t}_{0},\infty \right].\) Then,

$$L ({}^{C}{D}_{t}^{\alpha } \left(g\left(t\right)\right))={p}^{\alpha }L\left(g\left(t\right)\right)-{\sum }_{i=0}^{k-1}{p}^{\alpha -i-i}{g}^{\left(i\right)}\left(0\right),0<{\alpha }\le 1, k-1<\alpha \le k\in {\mathbb{N}}, $$
(2.6)

where \(L ({}^{C}{D}_{t}^{\alpha } \left(g\left(t\right)\right))\) denotes the Laplace transform of \(g\left(t\right).\)

Definition 5

For \({a}_{1},{a}_{2}\in {\mathbb{R}}^{+}\) and \(A\in {\mathbb{C}}^{n \times n}\) where \({\mathbb{C}}\) denotes complex plane, then

$$L \left\{{t}^{{a}_{2}-1}{E}_{{a}_{1},{a}_{2}}(A{t}^{{a}_{1}})\right\}=\frac{{p}^{{a}_{1}-{a}_{2}}}{{p}^{{a}_{1}}-A},\mathrm{where }{E}_{{a}_{1},{a}_{2}}:\mathrm{Mittag}-\mathrm{Leffler\,function}.$$
(2.7)

Lemma 1

Let us consider the fractional order system:

$${}^{C}{D}_{t}^{\alpha }\left(Y\left(t\right)\right)=\Phi \left(Y\right), {Y}_{{t}_{0}}=\left({{y}_{{t}_{0}}}^{1},{{y}_{{t}_{0}}}^{2},\dots ,{{y}_{{t}_{0}}}^{n}\right), {{y}_{{t}_{0}}}^{j} , j=\mathrm{1,2},\dots ,n$$

with \(0<{\alpha }<1, Y\left(t\right)=({y}^{1}\left(t\right),{y}^{2}\left(t\right),\dots , {y}^{n}\left(t\right))\) and\(\Phi \left(Y\right) :\left[{t}_{0},\infty \right]\to {\mathbb{R}}^{n\times n}\). For calculate the equilibrium points, we have \(\Phi \left(\mathrm{Y}\right)=0\). These equilibrium points are locally asymptotically stable iff each eigen value \({\lambda }_{j}\) of the Jacobian matrix \(J\left(Y\right)=\frac{\partial ({\Phi }_{1},{\Phi }_{2},\dots , {\Phi }_{n})}{\partial ({y}^{1},{y}^{2}, \dots , {y}^{n})}\) determined at the equilibrium points satisfy\(\left|\mathrm{arg}({\lambda }_{j})\right|>\frac{{\alpha }\pi }{2}\).

Lemma 2

Let \(g\left(t\right)\in {\mathbb{R}}^{+}\) be a differentiable function. Then,

$${}^{C}{D}_{t}^{\alpha }\left[g\left(t\right)-{g}^{*}-{g}^{*}\mathit{ln}\frac{g\left(t\right)}{{g}^{*}}\right]\le \left(1-\frac{{g}^{*}}{g\left(t\right)}\right){}^{C}{D}_{t}^{\alpha } \left(g\left(t\right)\right), {g}^{*}\in {\mathbb{R}}^{+},\forall \alpha \in \left(\mathrm{0,1}\right).$$

We analyze the \(SEIR\) model with vaccination in this presentation, utilizing the Caputo operator of order \(0<\alpha \le 1\).

$$ \begin{aligned} {}_{{}}^{C} D_{t}^{\alpha } S\left( t \right) & = \lambda - \beta SI - \mu S - \eta S \\ {}_{{}}^{C} D_{t}^{\alpha } E\left( t \right) & = \beta SI - \left( { \mu + k } \right) E \\ {}_{{}}^{C} D_{t}^{\alpha } I\left( t \right) & = kE - \left( { \mu + \gamma } \right)I \\ {}_{{}}^{C} D_{t}^{\alpha } R\left( t \right) & = \gamma I - \mu R + \eta S \\ \end{aligned} $$
(2.8)

The initial conditions are

$$S\left(0\right)= {S}_{0}> 0, E \left(0\right)={E}_{0}>0, I\left(0\right)= {I}_{0}> 0 \,\, \mathrm{and}\,\, R(0) = {R}_{0} \ge 0$$
(2.9)

Non-negativity and boundedness of Solutions

Proposition

The region \(\Omega =\{(S,E,I,R) \in {\mathbb{R}}^{4} : 0 < N \le \frac{\lambda }{\mu } \}\) is non-negative invariant for the model (2.8) for \(t\ge 0\).

Proof

We have.

$${}^{C}{D}_{t}^{\alpha } \left(S+E+I+R\right)\left(t\right)= \lambda -\mu \left(S+E+I+R\right)\left(t\right).$$
  • $${}^{C}{D}_{t}^{\alpha } N\left(t\right)= \Lambda -\mu N(t)$$
  • $${}^{C}{D}_{t}^{\alpha } N(t)+\mu N (t) = \Lambda . $$
    (2.10)

    Taking Laplace transform, we have

    $${p}^{\alpha }L\left(N\left(t\right)\right)-{p}^{\alpha -1} N\left(0\right)+ \mu L\left(N\left(t\right)\right)=\frac{\Lambda }{p}$$
  • $$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ L\left(N\left(t\right)\right)\left({p}^{\alpha +1} + \mu \right)= {p}^{\alpha } N\left(0\right)+ \Lambda $$
  • $$L\left(N\left(t\right)\right)= \frac{{p}^{\alpha } N\left(0\right) + \Lambda }{{p}^{\alpha +1} + \mu }=\frac{{p}^{\alpha } N\left(0\right)}{{p}^{\alpha +1} + \mu }+\frac{\Lambda }{{p}^{\alpha +1} + \mu }.$$
    (2.11)

Applying inverse Laplace transform, we get

$$N\left(t\right)=N\left(0\right) {E}_{\alpha , 1 }\left(-\mu {t}^{\alpha }\right)+\Lambda {t}^{\alpha } {E}_{\alpha , \alpha + 1 }\left(-\Lambda {t}^{\alpha }\right).$$

According to Mittag–Leffler function,

$${E}_{c, d}\left(z\right)=z {E}_{c, c+d}\left(z\right)+\frac{1}{\Gamma \left(d\right)}.$$

Hence, \(N\left(t\right)=\left(N\left(0\right)-\frac{\Lambda }{{\mu }_{0} }\right) {E}_{\alpha , 1}\left(-\mu {t}^{\alpha }\right)+\frac{\Lambda }{\mu }\).

$${\text{Thus }}\mathop {\lim }\limits_{{t \to \infty }}Sup N(t) \le \frac{\Lambda }{\mu}.$$
(2.12)

As a result, the functions S, E, I, and R are all non-negative.

Basic Reproduction Number

The basic reproduction number \({\mathfrak{R}}_{0}\) may be obtained from the maximum eigen value of the matrix \(F{V}^{-1}\) where,

\(F\) = \(\left[\begin{array}{cc}0& \frac{\beta \lambda }{\mu +\eta }\\ 0& 0\end{array}\right]\) and \(V\) = \(\left[\begin{array}{cc}\mu +k& 0\\ -k& \mu +\gamma \end{array}\right]\).

$${\text{Therefore the reproduction number }}{\mathfrak{R}}_{0} = \frac{k\beta \lambda }{\left(\mu +\eta \right)\left(\mu +k\right)(\mu +\gamma )}.$$
(2.13)

Stability Analysis

The system's equilibrium may be found by solving the system (2.8). The disease-free equilibrium points \({E}_{0}\) and the epidemic equilibrium point \({E}_{1}\) of the system (2.8) are obtained from

$${}^{C}{D}_{t}^{\alpha } S\left(t\right)={}^{C}{D}_{t}^{\alpha } E\left(t\right)={}^{C}{D}_{t}^{\alpha } I\left(t\right)={}^{C}{D}_{t}^{\alpha } R\left(t\right)=0.$$
(3.1)

The model (2.8) has two equilibrium points namely, \({E}_{0}\) = (\(\frac{\lambda }{\mu +\eta } , 0, 0, \frac{\lambda \eta }{\mu (\mu +\eta )}\)) and\({E}_{1} = ({S}^{*},{E}^{*},{I}^{*},{R}^{*})\),

where \({S}^{*}\) = \(\frac{\left(\mu +\gamma \right)(\mu +k)}{\beta k}\), \({E}^{*}=\frac{\left(\mu +\gamma \right){I}^{*}}{k}\), \({I}^{*}\) = \(\frac{\lambda k}{\left(\mu +\gamma \right)(\mu +k)}-\frac{\left(\mu +\eta \right)}{\beta }\),\({R}^{*}\) = \(\frac{\upgamma {I}^{*}+\eta {S}^{*}}{\upmu }\).

The Jacobian matrix \(( J\)) of the model (2.8) at \((S, E, I, R)\) is given by.

$$J =\left[\begin{array}{ccc}-\beta I-\mu -\eta & 0& \begin{array}{cc}-\beta S& 0\end{array}\\ \beta I& -(\mu +k)& \begin{array}{cc}\beta S&\quad 0\end{array}\\ \begin{array}{c}0\\ \eta \end{array}&\quad \begin{array}{c}k\\ 0\end{array}&\quad \begin{array}{cc}\begin{array}{llll}\quad -(\mu + \gamma )\\ \quad \gamma \end{array}&\quad \begin{array}{c}0\\ -\mu \end{array}\end{array}\end{array}\right].$$

3.1 Theorem

When \({\mathfrak{R}}_{0}\)< 1, the point \({E}_{0}\) of the system (2.8) is locally asymptotically stable, and when \({\mathfrak{R}}_{0}> 1\), it is unstable.

Proof

The Jacobian matrix \(J\) at \({E}_{0}\) becomes

\(J\)(\({E}_{0}\)) = \(\left[\begin{array}{ccc}-\mu -\eta & 0& -\begin{array}{cc}\frac{\beta \lambda }{\mu +\eta }&\quad 0\end{array}\\\quad 0& -(\mu +k)&\quad \begin{array}{cc}\frac{\beta \lambda }{\mu +\eta }&\quad 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}&\quad \begin{array}{c}k\\ 0\end{array}&\quad \begin{array}{cc}\begin{array}{c}-(\mu + \gamma )\\ \gamma \end{array}&\quad \begin{array}{c}0\\ -\mu \end{array}\end{array}\end{array}\right]\).

Now \((-\mu-\eta \)), \(-\mu \), \(-(\mu +\upgamma )\) and (\(\mu +k\)) (\({\mathfrak{R}}_{0}-1\)) are the roots of the characteristic equation. The equilibrium point \({E}_{0}\) is locally asymptotically stable or unstable according as

\({\mathfrak{R}}_{0}< 1\) or \({\mathfrak{R}}_{0}> 1\).

3.2 Theorem

If \({\mathfrak{R}}_{0}>1\) , the epidemic equilibrium \({E}_{1} = ({S}^{*},{E}^{*},{I}^{*},{R}^{*})\) is locally asymptotically stable.

Proof

\(T\)he Jacobian matrix \(J\) at \({E}_{1}\) becomes

$$J({E}_{1}) =\left[\begin{array}{ccc}-\beta {I}^{*}-\mu -\eta & 0& \begin{array}{cc}-\beta {S}^{*}& 0\end{array}\\ \beta {I}^{*}& -(\mu +k)&\quad \begin{array}{cc}\quad \beta {S}^{*}& \quad 0\end{array}\\ \begin{array}{c}\quad 0\\ \quad \eta \end{array}&\quad \begin{array}{c}k\\ \quad 0\end{array}&\quad \begin{array}{cc}\begin{array}{c}\quad -(\mu + \gamma )\\ \gamma \end{array}&\quad \begin{array}{c}\quad 0\\ \quad -\mu \end{array}\end{array}\end{array}\right].$$

The characteristic equation is (\(-\mu -x\)) (\({x}^{3}+a{x}^{2}+bx+c)\) = 0,

where

$$a = \beta {I}^{*}+ 3\mu + k + \gamma +\eta, $$
$$b = \left(\beta {I}^{*}+ \mu +\eta \right)\left(2\mu + k + \gamma \right)+ \left(\mu + k\right)\left( \mu + \gamma \right)-\beta k{S}^{*},$$
$$c=\left(\beta {I}^{*}+ \mu \right)\left(\mu + k\right)\left( \mu + \gamma \right)-(\mu +\eta )\beta k{S}^{*}.$$

Appling Routh-Hurwitz condition, the model (2.8) is locally asymptotically stable at \({E}_{1}\) as \(a > 0, b > 0, ab> c\).

3.3 Theorem

When \({\mathfrak{R}}_{0}\)< 1, the system (2.8) is globally asymptotically stable, and unstable when \({\mathfrak{R}}_{0}> 1\) at \({E}_{0}\).

Proof

Using the appropriate Lyapunov function

$${\mathcal{F}}={B}_{1}E+{B}_{2}I.$$

The aforementioned function's time fractional derivatives is

$${}^{C}{D}_{t}^{\alpha }\mathcal{F}\left(t\right) ={B}_{1} {}^{C}{D}_{t}^{\alpha } E\left(t\right)+{B}_{2} {}^{C}{D}_{t}^{\alpha } I(t).$$

From (2.8) we get,

$${}^{C}{D}_{t}^{\alpha }\mathcal{F}(t)={B}_{1}\left[ \beta SI - \left( \mu + k \right)E \right]+ {B}_{2} [ kE-\left( \mu + \gamma \right)I ].$$
(3.2)

Using little perturbation from (3.2) and (2.13), we have

$${B}_{1}=\lambda k {B}_{2}=(\mu +\eta )(\mu +k).$$

Now,

$${}^{C}{D}_{t}^{\alpha }\mathcal{F}(t)= \beta SI\lambda k-\left( \mu + \gamma \right)(\mu +\eta )(\mu +k)I$$
$$I [\left( \mu + \gamma \right)(\mu +\eta )\left(\mu +k\right)][\frac{\beta S\lambda k}{\left( \mu + \gamma \right)(\mu +\eta )\left(\mu +k\right)}-1].$$

Since \(S= \frac{\lambda }{\mu +\eta } \le N\), it follows that

$${}^{C}{D}_{t}^{\alpha } \mathcal{F}(t) \le I [\left( \mu + \gamma \right)(\mu +\eta )\left(\mu +k\right)][\frac{\beta \lambda k}{\left( \mu + \gamma \right)(\mu +\eta )\left(\mu +k\right)}-1]$$
(3.3)
$$\le I [\left( \mu + \gamma \right)(\mu +\eta )\left(\mu +k\right)][{\mathfrak{R}}_{0}-1].$$

Hence \({}^{C}{D}_{t}^{\alpha}\mathcal{F}\left(t\right)<0\) if \({\mathfrak{R}}_{0}< 1\). As a result of LaSalle's use of Lyapunov's concept [35, 58], the point \({E}_{0}\) is globally asymptotically stable and unstable if \({\mathfrak{R}}_{0}>1\).□

3.4 Theorem

The equilibrium point \({E}_{1}\) is globally asymptotically stable if \({\mathfrak{R}}_{0}>1\).

Proof

The non-linear Lyapunov function of the Goh-Volterra form is as follows:

$$V=\left(S-{S}^{*}-{S}^{*} log\frac{S}{{S}^{*}}\right)+\left(E-{E}^{*}-{E}^{*} log\frac{E}{{E}^{*}}\right)+Q(I-{I}^{*}-{I}^{*} log\frac{I}{{I}^{*}}).$$

Using Lemma 2 and taking Caputo derivative, we get

$${}^{C}{D}_{t}^{\alpha } V\left(t\right)\le \left(1-\frac{{S}^{*}}{S}\right){}^{C}{D}_{t}^{\alpha }S\left(t\right)+\left(1-\frac{{E}^{*}}{E}\right){}^{C}{D}_{t}^{\alpha } E\left(t\right)+Q\left(1-\frac{{I}^{*}}{I}\right){}^{C}{D}_{t}^{\alpha }\mathrm{ I}(\mathrm{t}).$$
(3.4)

Using system (2.8) we get,

$${}^{C}{D}_{t}^{\alpha } V\left(t\right)\le \left(\lambda - \beta SI - \mu S-\eta S-\frac{{S}^{*}(\lambda - \beta SI - \mu S-\eta S)}{S}\right)+\left((\beta SI - ( \mu + k ) E)-\frac{{E}^{*}(\beta SI - ( \mu + k ) E)}{E}\right)+Q((kE-( \mu + \gamma ) I)-\frac{{I}^{*}\left(kE-\left( \mu + \gamma \right)I\right)}{I}.$$
(3.5)

Equation (2.8) gives us the steady state,

$$\lambda = \beta {S}^{*}{I}^{*} + \mu {S}^{*}+\eta {S}^{*}.$$
(3.6)

Substituting Eq. (3.6) into (3.5) we have,

$$\begin{aligned}{}^{C}{D}_{t}^{\alpha } V\left(t\right)\le&\left(\beta {S}^{*}{I}^{*} + \mu {S}^{*}+\eta {S}^{*}- \beta SI -\mu S-\eta S\right.\nonumber\\&\left.-\frac{{S}^{*}(\beta {S}^{*}{I}^{*} + \mu {S}^{*}+\eta {S}^{*}- \beta SI - \mu S-\eta S)}{S}\right)\\&+\left((\beta SI - ( \mu + k ) E)-\frac{{E}^{*}(\beta SI - ( \mu + k ) E)}{E}\right)\\&+Q((kE-(\mu + \gamma ) I)-\frac{{I}^{*}(kE-( \mu + \gamma )I)}{I}).\end{aligned}$$

Further simplification gives,

$$\begin{aligned}{}^{C}{D}_{t}^{\alpha } V\left(t\right)\le&\left(\beta {S}^{*}{I}^{*} + \mu {S}^{*}+\eta {S}^{*} - \mu S-\eta S\right.\\&\left.-\frac{{S}^{*}(\beta {S}^{*}{I}^{*} + \mu {S}^{*}+\eta {S}^{*}-\beta SI - \mu S-\eta S)}{S}\right)\\&+\left( - ( \mu + k )E)-\frac{{E}^{*}(\beta SI - ( \mu + k ) E)}{E}\right)\\&+Q((kE-( \mu +\gamma ) I)-\frac{{I}^{*}(kE-( \mu + \gamma )I)}{I}).\end{aligned}$$
(3.7)

Taking all infected classes that do not have a single star (*) from (3.7) and equal to zero:

$${S}^{*}\beta I - \left( \mu + k \right)E+Q\left(kE-\left( \mu + \gamma \right)I\right)=0.$$
(3.8)

The steady state was slightly perturbed between (2.8) and (3.8), resulting in:

$$Q=\frac{{S}^{*}\beta }{\left( \mu + \gamma \right)},\left( \mu + k \right)=\frac{{I}^{*}{S}^{*}\beta }{{E}^{*}},k=\frac{{(\mu + \gamma )I}^{*}}{{E}^{*}}.$$
(3.9)

Using (3.9) into (3.7) gives:

$${}^{C}{D}_{t}^{\alpha } V\left(t\right) \le \left(\beta {S}^{*}{I}^{*} + \mu {S}^{*}+\eta {S}^{*} - \mu S-\frac{{S}^{*}(\beta {S}^{*}{I}^{*} + \mu {S}^{*} - \mu S-\eta S)}{S}\right)+\left(-\frac{{E}^{*}\beta SI }{E}+{I}^{*}{S}^{*}\beta \right)+(-\frac{{I}^{*}{S}^{*}E\beta {I}^{*}}{I{E}^{*}}+\beta {S}^{*}{I}^{*}).$$

Using A.M \(\ge \) G.M., we have \((2-\frac{s}{{S}^{*}}-\frac{{S}^{*}}{S})\le 0\), \((3-\frac{{S}^{*}}{S}-\frac{{I}^{*}E}{I{E}^{*}}-\frac{S{E}^{*}I}{E})\le 0\).

Thus \({}^{C}{D}_{t}^{\alpha } V\left(t\right) \le 0\) for \({\mathfrak{R}}_{0}>1\).

The point \({E}_{1}\) is globally asymptotically stable if \({\mathfrak{R}}_{0}>1\).□

Predictor–Corrector Technique for the \({\varvec{S}}{\varvec{E}}{\varvec{I}}{\varvec{R}}\) Model

The Adams–Bashforth-Moulton approach is the most extensively employed numerical approach for fractional order initial value circumstances.

Let us consider

$${}^{C}{D}_{t}^{\alpha } {L}_{j}\left(t\right)={g}_{j} \left(t, {L}_{j}\left(t\right)\right),{L}_{j}^{r}\left(0\right)={L}_{j0}^{r},$$
(4.1)
$$r=\mathrm{0,1},2,\dots , \lceil\alpha \rceil j\in {\mathbb{N}}$$

where \({L}_{j0}^{r}\in {\mathbb{R}}\) is equal to the well-known Volterra integral equation.

$${L}_{j}\left(t\right)= {\sum_{n=0}^{\lceil\alpha \rceil-1}L}_{j0}^{r}\frac{{t}^{n}}{n!}+\frac{1}{\Gamma ({\alpha }) }\underset{0}{\overset{t}{\int }} (t-u{)}^{\alpha -1}{g}_{j} \left(u, {L}_{j}\left(u\right)\right)du, j\in {\mathbb{N}}.$$
(4.1)

The algorithm is explained as follows

Let \(T=h\widehat{m}, {t}_{n}=nh, n=\mathrm{0,1},2,\dots ,\widehat{m}\).

Corrector formulae:

$${S}_{n+1}= {S}_{0}+ \frac{{h}^{{\alpha }_{1}}}{\Gamma \left({\alpha }_{1}+2\right)}\left(\lambda - \beta {S}_{n+1}^{p}{I}_{n+1}^{p}- \mu {S}_{n+1}^{p}-\eta {S}_{n+1}^{p}\right)+\frac{{h}^{{\alpha }_{1}}}{\Gamma \left({\alpha }_{1}+2\right)}\sum_{j=0}^{n}{\alpha }_{1,j,n+1 }\left(\lambda -\beta {S}_{j}{I}_{j}-\mu {S}_{j}-\eta {S}_{j}\right),$$
$${E}_{n+1}= {E}_{0}+ \frac{{h}^{{\alpha }_{2}}}{\Gamma ({\alpha }_{2}+2)}\left(\beta {S}_{n+1}^{p}{I}_{n+1}^{p}- (\mu +k){E}_{n+1}^{p}\right)+\frac{{h}^{{\alpha }_{2}}}{\Gamma ({\alpha }_{2}+2)}\sum_{j=0}^{n}{\alpha }_{2,j,n+1 }(\beta {S}_{j}{I}_{j}-(\mu +k){E}_{j}),$$
$${I}_{n+1}= {I}_{0}+ \frac{{h}^{{\alpha }_{3}}}{\Gamma ({\alpha }_{3}+2)}\left(k{E}_{n+1}^{p}-(\mu +\gamma ){I}_{n+1}^{p}\right)+\frac{{h}^{{\alpha }_{3}}}{\Gamma ({\alpha }_{3}+2)}\sum_{j=0}^{n}{\alpha }_{3,j,n+1 }(k{E}_{j}-(\mu +\gamma ){I}_{j}),$$
$${R}_{n+1}= {R}_{0}+ \frac{{h}^{{\alpha }_{4}}}{\Gamma ({\alpha }_{4}+2)}\left( \gamma {I}_{n+1}^{p}-\mu {R}_{n+1}^{p}+\eta {S}_{n+1}^{p}\right)+\frac{{h}^{{\alpha }_{4}}}{\Gamma ({\alpha }_{4}+2)}\sum_{j=0}^{n}{\alpha }_{4,j,n+1 }(\gamma {I}_{j}-\mu {R}_{j}+\eta {S}_{j}).$$
(4.3)

Predictor formulae:

$${S}_{n+1}^{p}= {S}_{0}+ \frac{1}{\Gamma ({\alpha }_{1})}\sum_{j=0}^{n}{\beta }_{1,j,n+1 }\left(\lambda -\beta {S}_{j}{I}_{j}-\mu {S}_{j}-\eta {S}_{j}\right),$$
$${E}_{n+1}^{p}= {E}_{0}+ \frac{1}{\Gamma ({\alpha }_{2})}\sum_{j=0}^{n}{\beta }_{2,j,n+1 }(\beta {S}_{j}{I}_{j}-(\mu +k){E}_{j}),$$
(4.4)
$${I}_{n+1}^{p}= {I}_{0}+ \frac{1}{\Gamma ({\alpha }_{3})}\sum_{j=0}^{n}{\beta }_{3,j,n+1 }(k{E}_{j}-(\mu +\gamma ){I}_{j}),$$
$${R}_{n+1}^{p}= {R}_{0}+ \frac{1}{\Gamma ({\alpha }_{4})}\sum_{j=0}^{n}{\beta }_{4,j,n+1 }(\gamma {I}_{j}-\mu {R}_{j}+\eta {S}_{j}),$$

where

$${\alpha }_{i,j,n+1 }=\left\{\begin{array}{ll}{n}^{\alpha +1}-\left(n-\alpha \right)(n+1{)}^{\alpha }, &\quad if j=0,\\ {(n-j+2)}^{\alpha +1}+(n-j{)}^{\alpha +1}-2(n-j+1{)}^{\alpha +1}, &\quad if 0\le j\le n,\\ 1, &\quad if j=1,\end{array}\right.$$

and

\({\beta }_{i,j,n+1}=\frac{{h}^{{\alpha }_{1}}}{\alpha }\) [\({(n+1-j)}^{{\alpha }_{1}}-\left(n-j{)}^{{\alpha }_{1}}\right] , 0\le j\le n\) and \(i=\mathrm{1,2},\mathrm{3,4}.\)

Numerical Study

In this part, we use the mathematical software to do rigorous numerical simulations of the findings produced by Adam's-Bashforth-Moulton predictor–corrector system. The model has been discussed in both the cases of without vaccine corresponding to \(\eta =0\) and with vaccine corresponding to \(\eta \ne 0\) (Fig. 1).

The estimated values of the parameters in the case of COVID-19 in India are as follows:

Figure 2 shows the behavior of susceptible individuals with time for different fractional order α in both cases of with and without vaccination. We observe that number of susceptible individuals decrease with time for all values of α. At a given period, however, the number of susceptible individuals grows as the value of decreases, suggesting that the fractional order derivatives of the dynamical variables produce greater benefits in determining the number of susceptible individuals. Moreover, the administration of vaccine shows that the number of susceptible individuals is always less than those in the case of without vaccination for different values of α as expected.

Fig. 1
figure 1

The \(SEIR\) model is depicted as a diagram

Full size image
Fig. 2
figure 2

Plots of S(t) for different values of \(\alpha =0.6, 0.8, 1.0\) with respect to time (days) with vaccination and without vaccination

Full size image

Figure 3 indicates the relation between exposed individuals and time for different fractional order α in both cases of with and without vaccination. We observe that number of exposed individuals increases with time for all values of α. However, at a fixed time \(t\) the number of exposed individuals decreases with a decrease in the value of α. Furthermore, the introduction of vaccination shows that the number of exposed individuals is less than those in the case of without vaccination for different values of α as expected.

Fig. 3
figure 3

Plots of E(t) for different values of \(\alpha =0.6, 0.8, 1.0\) with respect to time (days) with vaccination and without vaccination

Full size image

Figure 4 represents the behavior of number of infected individuals with time for different fractional order α in both cases of with and without vaccination. We observe that the number of infected individuals decreases consistently with time for different fractional values of \(\alpha \) which further decreases with the use of vaccines.

Fig. 4
figure 4

Plots of I(t) for various values of \(\alpha =0.6, 0.8, 1.0\) with respect to time (days) with vaccination and without vaccination

Full size image

The behavior of recovered individuals with time is shown in Fig. 5. It is evident from the graph that the number of recovered individuals increases with time for all values of \(\alpha \). It may also be deduced that the recovered individuals increase because of the impact of vaccines.

Fig. 5
figure 5

Plots of R(t) for different values of \(\alpha =0.6, 0.8, 1.0\) with respect to time (days) with vaccination and without vaccination

Full size image

Figure 6 show the time series analysis of the \(SEIR\) model with vaccination for \({\mathfrak{R}}_{0}=1.55\) and parameter values given in Table 1. The two equilibrium points are \({E}_{0}\) = (\(1.0520 , 0, 0, 1.4411\)) and\({E}_{1} = (\mathrm{0.6795,0.0825,0.0199,1.7104})\). It shows that with varying initial values, model system (2.5) has an endemic equilibrium and is globally asymptotically stable, confirming our theoretical results in Theorem 3.4.

Fig. 6
figure 6

Time series plot of all individuals with vaccination and various initial conditions, parameter values are given in Table 1

Full size image
Table 1 Estimated value of parameters
Full size table

Conclusion

In this article, we have discussed the fractional order derivatives with the Caputo operator of order \(0<\alpha \le 1\) of SEIR model with vaccination. Based on the COVID-19 cases data in India, collected up to 1st August, 2021, we estimated the basic reproduction number \({\mathfrak{R}}_{0}\mathrm{ without vaccination}\) to be 3.67 and with vaccination to be 1.55. Thus, it shows that introduction of the vaccination parameter \(\eta \) reduces the reproduction number \({\mathfrak{R}}_{0}\). The parameter values in (2.8) have been estimated using the real time data given in [59, 60] and is presented in Table 1. We have demonstrated the global stability of the equilibrium points by constructing the Lyapunov function. The choice of a derivative order is often more appropriate for modeling complex data due to its freedom and reduced error. This benefit can be utilized in real time data since the data is typically less accurate than the integer-ordered model.

As is evident from our study that vaccination is an effective method in control and prevention of the COVID-19 disease. The model described in this research may be used to investigate the dynamics of various epidemic illnesses, as well as the function of vaccination in successful transmission control. Our investigation suggests that the primary task of health officials, policymakers, and experts should be to implement the most appropriate vaccination plan to fight against the disease. It is very important that the transmission of diseases is controlled at an early stage to avoid a massive impact on the population. Some of the preventive measures that can be utilized are the enforcement of curfews, checkpoints, and containment zones. These can be used to prevent the spread of contamination.

The implications of interface reduction on epidemic dynamic nature are now being investigated. Our goal is to modify the SEIR compartmental model to account for the varying levels of population isolation.