Skip to main content
SpringerLink
Log in

A Numerical Method for Fractional Pantograph Delay Integro-Differential Equations on Haar Wavelet

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

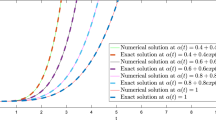
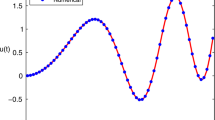
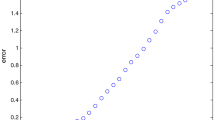
The main objective of this research work is devoted to study the solution of fractional pantograph delay integro-differential equations based on Haar wavelet collocation (HWC) technique. Through HWC algorithm, first we reduce the underlying equations to a system of algebraic equations. After getting a system of equations, Gauss elimination method is used for the solution of the mentioned problem. Under the techniques of functional analysis, we derive the necessary conditions for the existence and uniqueness of at most one solution of the considered problem. With the help of examples taken from the literature, we investigate the validation and convergence of the HWC method. In these examples, we compare the exact and approximate solutions for different fractional orders. Through tables, errors are calculated for different nodal points, we also compare the exact and approximate solutions for different fractional orders.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Kilbas, A.A., Marichev, O.I., Samko, S.G.: Fractional Integrals and Derivatives (Theory and Applications). Gordon and Breach, Switzerland (1993)

    MATH  Google Scholar 

  2. Zhang, L., Hou, W.: Standing waves of nonlinear fractional p-Laplacian Schrödinger equation involving logarithmic nonlinearity. Appl. Math. Lett. (2020). https://doi.org/10.1016/j.aml.2019.106149

    Article  MATH  Google Scholar 

  3. Wang, G., Pei, K., Chen, Y.: Stability analysis of nonlinear Hadamard fractional differential system. J. Frankl. Inst. 356, 6538–6546 (2019)

    Article  MathSciNet  Google Scholar 

  4. Zhang, L., Ahmad, B., Wang, G., Ren, X.: Radial symmetry of solution for fractional \(p\)-Laplacian system. Nonlinear Anal. (2020). https://doi.org/10.1016/j.na.2020.111801

    Article  MathSciNet  MATH  Google Scholar 

  5. Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)

    Book  Google Scholar 

  6. Benchohra, M., Bouriah, S., Nieto, J.J.: Existence and Ulam stability for nonlinear implicit differential equations with Riemann–Liouville fractional derivative. Demonstr. Math. 52(1), 437–450 (2019)

    Article  MathSciNet  Google Scholar 

  7. Li, D., Zhang, C.: Long time numerical behaviors of fractional pantograph equations. Math. Comput. Simul. 172, 244–257 (2020)

    Article  MathSciNet  Google Scholar 

  8. Wang, G., Pei, K., Agarwal, R., et al.: Nonlocal Hadamard fractional boundary value problem with Hadamard integral and discrete boundary conditions on a half-line. J. Comput. Appl. Math. 343, 230–239 (2018)

    Article  MathSciNet  Google Scholar 

  9. Kumar, A., Chauhan, H.V.S., Ravichandran, C., Nisar, K.S., Baleanu, D.: Existence of solutions of non-autonomous fractional differential equations with integral impulse condition. Adv. Differ. Equ. 2020(1), 1–14 (2020)

    Article  MathSciNet  Google Scholar 

  10. Shaikh, A., Tassaddiq, A., Nisar, K.S., Baleanu, D.: Analysis of differential equations involving Caputo–Fabrizio fractional operator and its applications to reaction–diffusion equations. Adv. Differ. Equ. 2019(1), 1–14 (2019)

    Article  MathSciNet  Google Scholar 

  11. Ghaffar, A., Ali, A., Ahmed, S., Akram, S., Junjua, M.D., Baleanu, D., Nisar, K.S.: A novel analytical technique to obtain the solitary solutions for nonlinear evolution equation of fractional order. Adv. Differ. Equ. 2020(1), 1–15 (2020)

    Article  MathSciNet  Google Scholar 

  12. Dineshkumar, C., Udhayakumar, R., Vijayakumar, V., Nisar, K.S.: Results on approximate controllability of neutral integro-differential stochastic system with state-dependent delay. Numer. Methods Partial Differ. Equ. (2020). https://doi.org/10.1002/num.22698

  13. Ahmad, O., Sheikh, N.A., Nisar, K.S., Shah, F.A.: Biorthogonal wavelets on the spectrum. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.7046

    Article  Google Scholar 

  14. Akbar, M., Nawaz, R., Ahsan, S., Nisar, K.S., et al.: New approach to approximate the solution for the system of fractional order Volterra integro-differential equations. Results Phys. 19, 103453 (2020)

    Article  Google Scholar 

  15. Jhangeer, A., Hussain, A., Junaid-U-Rehman, M., Ilyas, K., Baleanu, D., Nisar, K.S.: Lie analysis, conservation laws and travelling wave structures of nonlinear Bogoyavlenskii–Kadomtsev–Petviashvili equation. Results Phys. 19, 103492 (2020)

    Article  Google Scholar 

  16. Sedaghat, S., Ordokhani, Y., Dehghan, M.: Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun. Nonlinear Sci. Numer. Simul. 17(12), 4815–4830 (2012)

    Article  MathSciNet  Google Scholar 

  17. Bahsi, M., Cevik, M., Sezer, M.: Orthoexponential polynomial solutions of delay pantograph differential equations with residual error estimation. Appl. Math. Comput. 271, 11–21 (2015)

    Article  MathSciNet  Google Scholar 

  18. Hofer, P., Lion, A.: Modelling of frequency- and amplitude-dependent material properties of filler-reinforced rubber. J. Mech. Phys. Solids 57, 500–520 (2009)

    Article  Google Scholar 

  19. Rossetti, M., Bardella, P., Montrosset, I.: Modeling passive mode-locking in quantum dot lasers: a comparison between a finite-difference traveling-wave model and a delayed differential equation approach. IEEE J. Quantum Electron. 47(5), 569–576 (2011)

    Article  Google Scholar 

  20. Hale, J.K., Lunel, S.M.: Introduction to Functional Differential Equations. Springer, New York (2013)

    MATH  Google Scholar 

  21. Ahamad, I., Shah, K., Abdeljawad, T., Jarad, F.: Qualitative study of nonlinear coupled pantograph differential equations of fractional order. Fractals 1–16 (2020). https://doi.org/10.1142/S0218348X20400459

  22. Ahmad, I., Shah, K., Rahman, G.U., Baleanu, D.: Stability analysis for a nonlinear coupled system of fractional hybrid delay differential equations. Math. Methods Appl. Sci. 43, 8669–8682 (2020)

    Article  MathSciNet  Google Scholar 

  23. Alrabaiah, H., Ahmad, I., Shah, K., Rahman, G.U.: Qualitative analysis of nonlinear coupled pantograph differential equations of fractional order with integral boundary conditions. Bound. Value Probl. 2020(1), 1–13 (2020)

    Article  MathSciNet  Google Scholar 

  24. Ahmad, I., Nieto, J.J., Rahman, G.U., Shah, K.: Existence and stability for fractional order pantograph equations with nonlocal conditions. Electron. J. Differ. Equ. 2020(132), 1–16 (2020)

    MathSciNet  MATH  Google Scholar 

  25. Ali, A., Shah, K., Abdeljawad, T.: Study of implicit delay fractional differential equations under anti-periodic boundary conditions. Adv. Differ. Equ. 2020(1), 1–16 (2020)

    Article  MathSciNet  Google Scholar 

  26. Iqbal, M., Shah, K., Khan, R.A.: On using coupled fixed point theorems for mild solutions to coupled system of multi-point boundary value problems of nonlinear fractional hybrid pantograph differential equations. Math. Methods Appl. Sci. 44, 1–14 (2019)

    Google Scholar 

  27. Babolian, E., Shahsavaran, A.: Numerical solution of nonlinear Fredholm integral equations of the second kind using Haar wavelets. J. Comput. Appl. Math. 225, 87–95 (2009)

    Article  MathSciNet  Google Scholar 

  28. Chen, C., Hsiao, C.: Haar wavelet method for solving lumped and distributed-parameter systems. IEE Proc. Control Theory Appl. 144, 87–94 (1997)

    Article  Google Scholar 

  29. Lepik, U., Tamme, E.: Solution of nonlinear Fredholm integral equations via the Haar wavelet method. Proc. Estonian Acad. Sci. Phys. Math. 56(1), 17–27 (2007)

    MathSciNet  MATH  Google Scholar 

  30. Li, Y., Zhao, W.: Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Comput. 216, 2276–2285 (2010)

    Article  MathSciNet  Google Scholar 

  31. Lakshmikantham, V., Leela, S., Vasundhara, J.: Theory of Fractional Dynamic Systems. Cambridge Academic Publishers, Cambridge (2009)

    MATH  Google Scholar 

  32. Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)

    MATH  Google Scholar 

  33. Podlubny, I.: Fractional Differential Equations. Mathematics in Science and Engineering. Academic Press, New York (1999)

    MATH  Google Scholar 

  34. Lepik, U.: Solving fractional integral equations by the Haar wavelet method. Appl. Math. Comput. 214(2), 468–478 (2009)

    Article  MathSciNet  Google Scholar 

  35. Hamoud, A.A., Ghadle, K.P.: Modified Laplace decomposition method for fractional Volterra–Fredholm integro-differential equations. J. Math. Model. 6(1), 91–104 (2018)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

All authors are thankful to the reviewers for their careful reading of the paper and suggestions which has improved the paper very well.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Malakand, Chakdara Dir (Lower), Khyber Pakhtunkhawa, Pakistan

    Israr Ahmad & Kamal Shah

  2. Department of Mathematics, University of Peshawar, Peshawar, Khyber Pakhtunkhwa, Pakistan

    Rohul Amin

  3. Department of Mathematics and General Sciences, Prince Sultan University, Riyadh, Saudi Arabia

    Thabet Abdeljawad

  4. Department of Medical Research, China Medical University, Taichung, 40402, Taiwan

    Thabet Abdeljawad

  5. Department of Computer Science and Information Engineering, Asia University, Taichung, Taiwan

    Thabet Abdeljawad

Authors
  1. Israr Ahmad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rohul Amin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thabet Abdeljawad
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Kamal Shah
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors have read and approved the final version.

Corresponding author

Correspondence to Thabet Abdeljawad.

Ethics declarations

Conflict of interest

We have no conflict of interest regarding this research work.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahmad, I., Amin, R., Abdeljawad, T. et al. A Numerical Method for Fractional Pantograph Delay Integro-Differential Equations on Haar Wavelet. Int. J. Appl. Comput. Math 7, 28 (2021). https://doi.org/10.1007/s40819-021-00963-1

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40819-021-00963-1

Keywords

Search

Navigation