Nonlinear Scalar Perturbations of Extremal Reissner–Nordström Spacetimes

Abstract

We present the first rigorous study of nonlinear wave equations on extremal black hole spacetimes without any symmetry assumptions on the solution. Specifically, we prove global existence with asymptotic blow-up for solutions to nonlinear wave equations satisfying the null condition on extremal Reissner–Nordström backgrounds. This result shows that the extremal horizon instability persists in model nonlinear theories. Our proof crucially relies on a new vector field method that allows us to obtain almost sharp decay estimates.

Appendix A.

1.1 A.1. The Couch-Torrence Conformal Isometry

An extremal Reissner–Nordström spacetime of mass M admits a conformal isometry called the Couch-Torrence first introduced in [25] that in ingoing Eddington-Finkelstein coordinates is given by

$$\begin{aligned} {\bar{\Phi }} ( v,r,\omega ) \doteq \left( u = v , r' = M + M^2 (r-M)^{-1} , \omega \right) , \end{aligned}$$

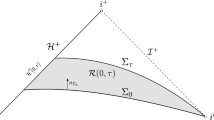
and through it ${\mathcal {H}}^{+}$ is mapped onto ${\mathcal {I}}^{+}$.

1.2 A.2. The d’Alembertian in Different Coordinates

The nonlinearity of (1.1) can be written as follows in double null coordinates (where $\phi = r \psi$):

(A.1)

Equation (1.1) can then be written in terms of $\phi = r \psi$ as follows in double null coordinates:

(A.2)

1.3 A.3. Basic Inequalities

We record some basic inequalities. The first is the Sobolev inequality on the sphere from which we have that for any smooth function f:

$$\begin{aligned} \int _{{\mathbb {S}}^2} f^2 \, d\omega \lesssim \sum _{k \le 2}\int _{{\mathbb {S}}^2} ( \Omega ^k f )^2 \, d\omega . \end{aligned}$$

(A.3)

The second one is Hardy’s inequality, which close to the horizon it has the following form for a smooth function f and for any $s \ne 1$ and for any $M \le r_1< r_2 < \infty$:

$$\begin{aligned}&\int _{u_{r_2} (v)}^{u_{r_1} (v)} (r-M)^{-s} f^2 \, du \lesssim \frac{1}{(1+s)^2} \int _{u_{r_2} (v)}^{u_{r_1} (v)} (r-M)^{-s-2} ({\underline{L}} f )^2 \, du\nonumber \\&\qquad + 2 (r_1 - M )^{-s-1} f^2 ( u_{r_1} (v) , v) , \end{aligned}$$

(A.4)

and close to infinity it gives us that for any $M< r_1 < r_2 \le \infty$:

$$\begin{aligned} \int _{v_{r_1} (u)}^{v_{r_2} (u)} r^s f^2 \, dv \lesssim \frac{1}{(1+s)^2} \int _{v_{r_1} (u)}^{v_{r_2} (u)} r^{s+2} (L f )^2 \, dv + 2 r^{s+1} f^2 (u , v_{r_2} (u)) , \end{aligned}$$

(A.5)

where in the case of the horizon if $r_1 = M$ then the last term is considered as:

$$\begin{aligned} 2 \lim _{u \rightarrow \infty } (r - M )^{-s-1} f^2 ( u_{r} (v) ,\qquad \end{aligned}$$

and in the case of infinity if $r_2 = \infty$ then the last term is considered as:

$$\begin{aligned} 2 \lim _{v \rightarrow \infty } r^{s+1} f^2 (u , v_{r} (u)) . \end{aligned}$$

For proofs of these inequalities see [7].

1.4 A.4. Elliptic Estimates

We record as well the following basic elliptic estimate from [11]:

$$\begin{aligned} \begin{aligned} \int _{\Sigma _{\tau } \cap \{ r\ge r_0 > M \}} (\partial _a \partial _b \psi )^2 d\mu _{\Sigma } \lesssim&\int _{\Sigma _{\tau } \cap \{ r\ge r_0 \}} J^T_{\mu } [\psi ] \cdot \mathbf{n }_{\Sigma } d\mu _{\Sigma } \\&+ \int _{\Sigma _{\tau } \cap \{ r\ge r_0 \}} J^T_{\mu } [T\psi ] \cdot \mathbf{n }_{\Sigma } d\mu _{\Sigma } + \int _{\Sigma _{\tau } \cap \{ r\ge r_0 \}} |F|^2 d\mu _{\Sigma } , \end{aligned} \end{aligned}$$

(A.6)

for any fixed $r_0 > M$, and any $\partial _a , \partial _b \in \{ L , {\underline{L}} , \partial _{\theta }, \partial _{\sigma } \}.$

1.5 A.5. Additional Norms

For any smooth function $f : {\mathcal {M}} \rightarrow {\mathbb {R}}$ we define for any $\tau \in [ \tau _0 , \infty )$ the norm:

$$\begin{aligned}&E^{\tau } [ f ] \doteq \int _{\Sigma _{\tau }} f^2 \, d\mu _{\Sigma _{\tau }} + \sum _{\begin{array}{c} k \le 5 \\ l \le 5 \end{array} } \int _{\Sigma _{\tau }} J^T [ \Omega ^k T^l f ] \cdot \mathbf{n }_{\Sigma _{\tau }} \, d\mu _{\Sigma _{\tau }} \\&\qquad +\int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-3+\delta _1} ( {\underline{L}} f_0 )^2 \, d\omega du + \int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-1+\delta _1} \left( {\underline{L}} \left( \frac{2r}{D} {\underline{L}} f_0 \right) \right) ^2 \, d\omega du \\&\qquad + \int _{{\mathcal {N}}_{\tau }^I} r^{3-\delta _1} ( L f_0 )^2 \, d\omega dv + \int _{{\mathcal {N}}_{\tau }^I} r^{1-\delta _1} \left( L \left( \frac{2r^2}{D} L f_0 \right) \right) ^2 \, d\omega dv\\&\qquad + \sum _{k \le 5} \Bigg [ \int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-3-\delta _2} ( {\underline{L}} \Omega ^k f_{\ge 1} )^2 \, d\omega du \\&\qquad + \int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-1-\delta _2} \left( {\underline{L}} \left( \frac{2r}{D} {\underline{L}} \Omega ^k f_{\ge 1} \right) \right) ^2 \, d\omega du \\&\qquad + \int _{{\mathcal {N}}_{\tau }^I} r^{3+\delta _2} ( L \Omega ^k f_{\ge 1} )^2 \, d\omega dv + \int _{{\mathcal {N}}_{\tau }^I} r^{1+\delta _2} \left( L \left( \frac{2r^2}{D} L \Omega ^k f_{\ge 1} \right) \right) ^2 \, d\omega dv \\&\qquad +\int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-3-\delta _2} ( {\underline{L}} \Omega ^k T f )^2 \, d\omega du \\&\qquad + \int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-1-\delta _2} \left( {\underline{L}} \left( \frac{2r}{D} {\underline{L}} \Omega ^k T f \right) \right) ^2 \, d\omega du \\&\qquad + \int _{{\mathcal {N}}_{\tau }^I} r^{3+\delta _2} ( L\Omega ^k T f )^2 \, d\omega dv + \int _{{\mathcal {N}}_{\tau }^I} r^{1+\delta _2} \left( L \left( \frac{2r^2}{D} L \Omega ^k T f \right) \right) ^2 \, d\omega dv \\&\qquad +\int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-2-\delta _2} ( {\underline{L}} \Omega ^k T^2 f )^2 \, d\omega du \\&\qquad + \int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-\delta _2} \left( {\underline{L}} \left( \frac{2r}{D} {\underline{L}} \Omega ^k T^2 f \right) \right) ^2 \, d\omega du \\&\qquad + \int _{{\mathcal {N}}_{\tau }^I}r^{2+\delta _2} ( L\Omega ^k T^2 f )^2 \, d\omega dv + \int _{{\mathcal {N}}_{\tau }^I} r^{\delta _2} \left( L \left( \frac{2r^2}{D} L \Omega ^k T^2 f \right) \right) ^2 \, d\omega dv \\&\qquad +\int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-2} ( {\underline{L}} \Omega ^k T^3 f )^2 \, d\omega du + \int _{{\mathcal {N}}_{\tau }^I} r^2 ( L\Omega ^k T^3 f )^2 \, d\omega dv \\&\qquad + \int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-1-\delta _2} ( {\underline{L}} \Omega ^k T^4 f )^2 \, d\omega du + \int _{{\mathcal {N}}_{\tau }^I} r^{1+\delta _2} ( L\Omega ^k T^4 f )^2 \, d\omega dv \\&\qquad + \int _{{\mathcal {N}}_{\tau }^H} (r-M)^{-1-\delta _2} ( {\underline{L}} \Omega ^k T^5 f )^2 \, d\omega du + \int _{{\mathcal {N}}_{\tau }^I} r^{1+\delta _2} ( L\Omega ^k T^5 f )^2 \, d\omega dv . \end{aligned}$$

Moreover we also define the standard Sobolev norms for any $s \in {\mathbb {N}}$ as:

$$\begin{aligned} \Vert f \Vert _{H^s_{\tau }} \doteq \sum _{| \alpha | \le s} \left( \int _{\Sigma _{\tau }} ( \partial ^{\alpha } f )^2 \, d\mu _{\Sigma _{\tau }} \right) ^{1/2}\ \text { and } \ \ \Vert f \Vert _{{\widetilde{H}}^s_{\tau }} \doteq \sum _{| \alpha | \le s} \left( \int _{\Sigma ^{int}_{\tau }} ( \partial ^{\alpha } f )^2 \, d\mu _{\Sigma ^{int}_{\tau }} \right) ^{1/2} , \end{aligned}$$

where $\partial \in \{T , Y , \partial _{\theta }, \partial _{\varphi } \}$.