Abstract
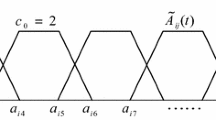
This paper addresses the approximation properties of the smooth fuzzy models. It is widely recognized that the fuzzy models can approximate a nonlinear function to any degree of accuracy in a convex compact region. However, in many applications, it is desirable to go beyond that and acquire a model to approximate the nonlinear function on a smooth surface to gain better performance and stability properties. Especially in the region around the steady states, when both error and change in error are approaching zero, it is much desired to avoid abrupt changes and discontinuity in the approximation of the input–output mapping. This problem has been remedied in our approach by application of the smooth compositions in the fuzzy modeling scheme. In the fuzzy decomposition stage of fuzzy modeling, we have discretized the parameters and then calculated the result through partitioning them into a dense grid. This could enable us to present the formulations by convolution and Fourier transformation of the parameters and then obtain the approximation properties by studying the structural properties of the Fourier transformation and convolution of the parameters. We could show that, irrespective to the shape of the membership function, one can approximate the dynamics and derivative of the continuous systems together, using the smooth fuzzy structure. The results of the paper have been tested and evaluated on a discrete event system in the hybrid and switched systems framework.




Similar content being viewed by others
References
Czogala, E., Pedrycz, W.: On identification in fuzzy systems and its application in control problems. Fuzzy Sets Syst. 6(1), 73–83 (1981)
Dubois, D., Prade, H.: Fuzzy Systems and Systems, Theory and Applications. Academic Press, New York (1981)
King, P.J., Mamdani, E.H.: The application of fuzzy control systems to industrial processes. Automatica 13(3), 235–242 (1977)
Kruger, J.J., Shaw, I.S.: The application of a new fuzzy model identification technique to a human control operator. In: 9th IFAC/IFORS Symposium on System Identification and Control, Budapest, Hungary, vol. 2 (6), pp. 1266–1271 (1991)
Ridley, J.N., Shaw, I.S., Kruger, J.J.: A probabilistic fuzzy model for dynamic systems. Electron. Lett. 12(24), 890–892 (1988)
Kreinovich, V., Nguyen, H.T., Yam, Y.: Fuzzy systems are universal approximators for a smooth function and its derivatives. Int. J. Intell. Syst. 15(6), 565–574 (1999)
Bezdek, J.: Fuzzy models–what are they, and why? IEEE Trans. Fuzzy Syst. 1(1), 1–5 (1993)
Mamadani, E.H.: Advances in the linguistic synthesis of fuzzy controllers. Int. J. Man Mach. Stud. 8(6), 669–678 (1976)
Kosko, B.: Fuzzy systems as universal approximators. IEEE Trans. Comput. 43(11), 1329–1333 (1994)
Wu, D., Mendel, J.M.: On the continuity of type-1 and interval type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 19(1), 179–192 (2011)
Wang, L.X., Mendel, J.M.: Fuzzy basis functions, universal approximation, and orthogonal least-squares learning. IEEE Trans. Neural Netw. 3, 807–813 (1992)
Courant, R., John, F.: Introduction to Calculus and Analysis, vol. II/1. Springer, New York (1999)
Castro, J.L.: Fuzzy logic controllers are universal approximators. IEEE Trans. Syst. Man Cybern. 25(4), 629–635 (1995)
Ashtiani, A.A., Menhaj, M.B.: Some new smooth fuzzy relational compositions. J. Math. Comput. Sci. 2(4), 717–722 (2011)
Ashtiani, A.A., Menhaj, M.B.: Introducing the fuzzy relational hybrid model as a building block for intelligent modeling of hybrid dynamical systems. IEEE Trans. Fuzzy Syst. 23, 1971–1983 (2015)
Askari M.A., Menhaj, M.B.: Fuzzy model predictive control based on modified fuzzy relational model. In: 13th Iranian Conference on Fuzzy Systems(IFSC) (2013)
Cheng, L., Rao, C., Chen, L.: Multidimensional knapsack problem based on uncertain measure. Sci. Iran. E 24(5), 2527–2539 (2017)
Chen, L., Peng, J., Zhang, B., Li, S.: Uncertain programming model for uncertain minimum weight vertex covering problem. J. Intellect. Manuf. 28(3), 625–632 (2017)
Chen, L., Peng, J., Zhang, B., Rosyida, I.: Diversified models for portfolio selection based on uncertain semivariance. Int. J. Syst. Sci. 48(3), 637–648 (2017)
Chen, L., Peng, J., Zhang, B.: Uncertain goal programming models for bicriteria solid transportation problem. Appl. Soft Comput. 51, 49–59 (2017)
Chen, L., Peng, J., Liu, Z., Zhao, R.: Pricing and effort decisions for a supply chain with uncertain information. Int. J. Prod. Res. 55(1), 264–284 (2017)
Fuller, R.: Fuzzy Reasoning and Fuzzy Optimization. Turku Centre for Computer Science, available on line (1998)
Rudin, W.: Principles of Mathematical Analysis. McGraw-Hill, New York (1976)
Osgood, B.: The Fourier Transform and Its Applications, Course Note EE 261. Electrical Engineering Department, Stanford University (2007)
Bracewell, R.N.: The Fourier Transform and Its Applications. McGraw Hill, New York (1986)
Branicky, M.S.: Introduction to hybrid systems. In: Hristu-Varsakelis, D., Levine, W. (eds.) Handbook of Networked and Embedded Control Systems, pp. 91–116. Birkhauser, Boston (2005)
Sadjadi, E., Herrero, J.G., Molina, J.M.: Smooth Fuzzy Model Identification and Model Predictive Control for Dynamic Systems, Unpublished report. Universidad de Carlos III
Simon, D.: Design rule base reduction of a fuzzy filter for the estimation of motor currents. Int. J. Approx. Reason. 25, 145–167 (2000)
Yam, Y., Baranyi, P., Yang, C.: Reduction of fuzzy rule base via singular value decomposition. IEEE Trans. Fuzzy Syst. 7, 120–132 (1999)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sadjadi, E.N., Garcia Herrero, J., Manuel Molina, J. et al. On Approximation Properties of Smooth Fuzzy Models. Int. J. Fuzzy Syst. 20, 2657–2667 (2018). https://doi.org/10.1007/s40815-018-0500-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40815-018-0500-9