Modeling the effect of sanitation in a human habitat to control the spread of bacterial diseases

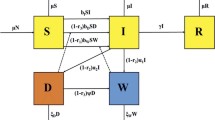
Abstract

The improper and poor sanitation, unclean drinking water and lack of hygiene are the key factors that affect the spread of various infectious diseases such as tuberculosis, typhoid fever,and cholera. In this paper, the effect of sanitation effort to control the spread of bacterial diseases is modeled and analyzed. In the modeling process, the total human population in the habitat is divided into two classes of susceptibles and infectives. The disease is assumed to spread directly by contact of susceptibles with infectives and indirectly by bacteria released by infectives in the environment affecting the susceptibles. It is assumed that the bacterial population density is directly proportional to the infective population. To mitigate the bacteria population present in the environment, suitable sanitation effort is applied to keep the environment clean so that the spread of disease could be controlled. The sanitation effort applied is modeled logistically, the intrinsic growth of which is assumed to be directly proportional to the density of bacteria present in the environment. The proposed model is analyzed using the stability theory of differential equations and numerical simulation. The analysis of the model reveals that by increasing the rate of sanitation effort, the bacteria population in the environment declines. This decrease in bacteria population in the environment ultimately decreases the infective population. Thus, the spread of bacterial diseases can be controlled if suitable sanitation effort is applied to curtail the bacterial population in the environment.

Appendices

Appendix 1

Proof

The general variational matrix M for model system (2) is given as follows:

$$\begin{aligned} M= \begin{bmatrix} \beta N -2\beta Y -\lambda B -(d+\alpha +\nu )& \quad \beta Y +\lambda B&\quad \lambda N - \lambda Y&\quad 0 \\ -\alpha&\quad -d&\quad 0&\quad 0\\ \theta&\quad 0&\quad - \theta _0 - \theta _1 F_{\text {s}}&\quad -\theta _1 B\\ 0&\quad 0&\quad \phi F_{\text {s}} - \phi _1 F_{\text {s}}&\quad \phi B - 2 \phi _0 F_{\text {s}} - \phi _1 B + \phi _{\text {s}}. \end{bmatrix} \end{aligned}$$

Let $M_i$ be the matrix M, evaluated at the equilibria $E_i$ ($i=0,1,2$).

The variational matrix $M_{0}$ of model (2) corresponding to $E_{0}(0, \frac{A}{d}, 0, 0)$ is given by

$$\begin{aligned} M_{0}= \begin{bmatrix} \frac{\beta A}{d} - (\nu + \alpha + d)&\quad 0&\quad \frac{\lambda A}{d}&\quad 0\\ -\alpha&\quad -d&\quad 0&\quad 0\\ \theta&0&\quad -\theta _{0}&\quad 0\\ 0&\quad 0&\quad 0&\quad \phi _{\text {s}}. \end{bmatrix} \end{aligned}$$

The characteristic polynomial of above matrix is given by

$$\begin{aligned}&(\phi _{\text {s}} - \mu ) (d + \mu ) (\mu ^2 - h_{1} \mu - h_{2})=0 \ {\text {where}},\\&h_{1} = \frac{\beta A}{d} - (\nu + \alpha + d) - \theta _{0},\\&h_{2} = \frac{\lambda A \theta }{d} + \theta _{0} \left(\frac{\beta A}{d} - (\nu + \alpha + d)\right)\\&\mu = \phi _{\text {s}}, -d .\\ \end{aligned}$$

From here, it is seen that equilibrium $E_0$ is unstable.

The variational matrix $M_{1}$ of model (2) corresponding to $E_{1}({\overline{Y}}, {\overline{N}}, {\overline{B}}, 0)$ is given by

$$\begin{aligned} M_{1}= \begin{bmatrix} \beta {\overline{N}} -2 \beta {\overline{Y}} - \lambda {\overline{B}} - (\nu + \alpha + d)&\quad \beta {\overline{Y}} + \lambda {\overline{B}}&\quad \lambda {\overline{N}} - \lambda {\overline{Y}}&\quad 0\\ -\alpha&\quad -d&\quad 0&\quad 0\\ \theta&\quad 0&\quad -\theta _{0}&\quad -\theta _{1} {\overline{B}}\\ 0&\quad 0&\quad 0&\quad (\phi - \phi _{1}) {\overline{B}}+\phi _{\text {s}}. \end{bmatrix} \end{aligned}$$

The fourth eigen value, i.e, $((\phi - \phi _{1}) {\overline{B}} + \phi _{\text {s}})$ is always positive (since $\phi > \phi _{1}$) showing that equilibrium $E_1$ is unstable.

The variational matrix $M_{2}$ of model (2) corresponding to $E_{2}(0, \frac{A}{d}, 0, \frac{\phi _{\text {s}}}{\phi _0})$ is given by

$$\begin{aligned} M_{2}= \begin{bmatrix} \frac{\beta A}{d} - (\nu + \alpha + d)&\quad 0&\quad \frac{\lambda A}{d}&\quad 0\\ -\alpha&\quad -d&\quad 0&\quad 0\\ \theta&\quad 0&\quad -\theta _{0}- \frac{\theta _1 \phi _{\text {s}}}{\phi _0}&\quad 0\\ 0&\quad 0&\quad (\phi - \phi _1) \frac{\phi _{\text {s}}}{\phi _0}&\quad -\phi _{\text {s}}. \end{bmatrix} \end{aligned}$$

The characteristic polynomial of above matrix is given by

$$\begin{aligned}&\mu ^2 - h_1 \mu - h_2 = 0\quad {\text {where}},\\&h_1= \left( \frac{\beta A}{d} - (\nu + \alpha + d)\right) - \left( \theta _0 + \frac{\theta _1 \phi _{\text {s}}}{\phi _0}\right) \\&h_2 = \frac{\lambda A \theta }{d} + \left( \theta _0 + \frac{\theta _1 \phi _{\text {s}}}{\phi _0}\right) \left( \frac{\beta A}{d} - (\nu + \alpha +d).\right) \ \end{aligned}$$

Using Routh–Hurwitz criteria, we get that $E_{2}$ is unstable if $R_{0}> 1$ and stable if $R_{0}< 1$.

To establish the local stability of endemic equilibrium $E^*$, we linearize the system using small perturbations y, n, b, $f_{\text {s}}$ about $E^*$, defined as follows: Y= y+Y*, N= n+N*, B= b+B* and Fs= fs + Fs* 

Consider the following positive definite function:

$$\begin{aligned} U_{1} = \frac{1}{2} (m_{0} y^2 + m_{1} n^2 + m_{2} b^2 + m_{3} f_{\text {s}}^2), \end{aligned}$$

where $m_{i}$ ($i = 0, 1, 2, 3$) are positive constants. Differentiating the above equation w.r.t ‘t’ and using linearized system of model (2) corresponding to $E^*$, we get

$$\begin{aligned} \dfrac{{\text {d}}U_{1}}{{\text {d}}t} &= - m_{0} \left( \beta Y^* + \lambda B^* + \lambda (N^* - Y^*)\frac{B^*}{Y^*}\right) y^2 - m_{1} d n^2 \\& \quad - m_{2} (\theta _{0} + \theta _{1} F_{\text {s}}^*) b^2 - m_{3} \phi _{0} F_{\text {s}}^* f_{\text {s}}^2 \\&\quad + [m_{0} (\beta Y^* + \lambda B^*) - m_{1} \alpha ] ny \\&\quad + [m_{0} \lambda (N^* - Y^*) + m_{2} \theta ]yb \\&\quad + [m_{3} (\phi - \phi _{1}) F_{\text {s}}^* - m_{2} \theta _{1} B^*] b f_{\text {s}}. \end{aligned}$$

After choosing $m_{0} = 1, m_{1} = \frac{\beta Y^* + \lambda B^*}{\alpha }$, $m_{2} = \frac{\lambda (N^* - Y^*)}{\theta }$ and $m_{3} = \frac{\lambda \theta _{1} B^* (N^* - Y^*)}{(\phi - \phi _{1}) \theta F_{\text {s}}^*}$, we get $\frac{{\text {d}}U_{1}}{{\text {d}}t}$ to be negative definite showing that $U_1$ is a Lyapunov function and hence $E^*$ is locally asymptotically stable provided condition (13) is satisfied.

Appendix 2

Proof

Consider the following positive definite function, corresponding to the model system (2) about $E^*$,

$$\begin{aligned} U_{2}= & {} \frac{m_0}{2}(Y-Y^*)^2+\frac{m_{1}}{2} (N - N^*)^2 + \frac{m_{2}}{2} (B - B^*)^2 \\&+ m_{3} \left( F_{\text {s}} - F_{\text {s}}^* -F_{\text {s}}^* \ln \frac{F_{\text {s}}}{F_{\text {s}}^*} \right) , \end{aligned}$$

where $m_{i}$ ($i = 0, 1, 2, 3$) are positive constants.

Differentiating the above equation w.r.t ‘t’ and using (2), we get

$$\begin{aligned}\dfrac{{\text {d}}U_{2}}{{\text {d}}t} &= -m_0 (\beta Y + \lambda B)(Y - Y^*)^2 - m_2 \theta _1 F_{\text {s}}(B-B^*)^2\\&\quad -m_0(\beta Y^* + d+\alpha +\nu - \beta N)(Y-Y^*)^2\\&\quad- d m_{1} (N - N^*)^2 -m_{2}\theta _{0} (B - B^*)^2 \\&\quad -m_{3} \phi _{0} (F_{\text {s}} - F_{\text {s}}^*)^2 \\&\quad + (m_{0}(\beta Y^* +\lambda B^*)- m_2 \alpha )(N - N^*) (Y - Y^*) \\&\quad + (- \lambda m_{0}(Y^* - N) + \theta m_{2}) (B - B^*) (Y - Y^*) \\&\quad + (-\theta _{1} B^* m_{2} + m_{3} (\phi - \phi _{1})) (B - B^*) (F_{\text {s}} - F_{\text {s}}^*). \end{aligned}$$

After choosing $m_{0} = 1, m_{1} = \dfrac{\beta Y^* + \lambda B^*}{\alpha }, m_{2} = \frac{\lambda (Y^* + \frac{ A}{d})}{\theta } and m_{3} = \frac{\theta _1 B^*}{(\phi -\phi _1)} m_2$, we get $\frac{{\text {d}}U_{2}}{{\text {d}}t}$ to be negative definite showing that $U_2$ is a Lyapunov function and hence $E^*$ is nonlinearly asymptotically stable provided conditions (14) is satisfied.