An unstandardized selective variance reduction script for elevation, latitude and longitude decorrelation stretch of multi-temporal LST imagery

Abstract

A selective variance reduction (SVR) script is presented that applies linear regression models to the principal components (PCs) of multi-temporal night monthly averaged land surface temperature (LST) imagery, in an attempt to spit the variance associated to elevation, latitude, longitude. The recently released version 6, MODIS LST data (MYD11C2) with spatial resolution 0.05° is used while the method is applied in SW USA. The innovation relies on the use of un-standardized PCs. Thus, the reconstructed LST should express the deviation in degrees Celsius, from the elevation, latitude, longitude predicted LST. The reconstructed data quantifies the temporal and spatial patterns of thermal anomalies. The modeling of the frequency distributions of the reconstructed LST imagery indicate that possibly snow melting and variations in water table depth are associated to the negative thermal anomaly observed during the Spring. The GNU OCTAVE 4.0 SVR software implementation is available at http://selective-variance-reduction.sourceforge.net for testing and evaluation.

Introduction

Currently land surface temperature (LST) data sets are computed from the satellite-based remotely sensed images with high temporal resolution at a moderate resolution scale, allowing the day and night monitoring of earth’s surface (Wan, 2013; 2014). An example being the LST acquisitions from MODerate-resolution Imaging Spectroradiometer (MODIS) on board the Aqua satellite (Liu et al. 2015; Miliaresis 2014b).

The LST data sets can be used to forward many research questions in landscape modelling (Voinov et al. 2004), in hydrologic processes simulation (Guo et al. 2016), in climate change research (Wilcke and Bärring 2016), in vegetation growth studies (Miliaresis 2014b).

The identification and mapping of thermal anomalies is a key issue in environmental analysis (Friedel 2012; Li et al. 2010). Miliaresis (2009) defined LST anomalies from a time series of LST imagery as regions presenting significantly higher or lower LST than their surrounding area. On the other hand, LST is correlated to elevation (H), latitude (LAT), and longitude (LON) so the quantification of thermal anomalies in vast regions is difficult (Miliaresis 2012c). In this context, Miliaresis (2012a, b) presented a method for H, LAT, LON decorrelation stretch of multi-temporal night monthly LST imagery. The method was extended to account for distance form the coastline and applied in vast regions in Zagros Ranges (Miliaresis 2013) and in Antarctica (Miliaresis 2014a).

In the previous research efforts (Miliaresis 2012a, b, c, 2013, 2014a) the computation of PCs from the cross-correlation matrix resulted in the expression of thermal anomalies as normal scores and limited the environmental applications of the method. In addition the evaluation of thematic information content of the reconstructed imagery was based on the interpretation of the spatial pattern (cluster maps) and the temporal pattern (cluster centroids). Clustering applies a short of generalization that under certain circumstances could hide data characteristics (Miliaresis 2013, 2014a). Thus, there is the need to study and model the frequency distributions of the reconstructed LST data in an attempt to quantify the thermal anomalies.

A major improvement has been applied to the MODIS data products since a new processing algorithm is applied (Wan 2013) and the version 6 data products (Wan 2014) are gradually released to the public (MYD11C2.006 2016). Thus, there is also the need to evaluate the version 6, MODIS LST data in the context of SVR method.

The software implementation of the SVR method as well as data for a specific study area are not available to the public for testing and evaluation purposes. On the hand, the freely available version 4.0 of GNU OCTAVE data analysis and data modeling software is released (Octave 2015) that runs under any operating system (Windows, Linux and Mac OS X). Octave 4.0 includes a graphical user interface, support for object-oriented programming, better compatibility with Matlab, and many new and improved functions.

The aim of this research effort is to implement the H, LAT, LON decorrelation stretch algorithm into OCTAVE 4.0 environment in an attempt to provide a tool that will allow the wide application of the SVR method to various scientific fields. The method is tested with new version MODIS LST data (MYD11C2.006 2016), in SW USA.

In methodological terms, an un-standardized variant of the SVR method is defined and used in attempt to express thermal anomalies in the reconstructed imagery as deviation in degrees Celsius, from the elevation, latitude, longitude predicted LST. In addition, the modeling of the frequency distributions of the reconstructed imagery will possibly reveal hidden thermal anomaly characteristics in the study area.

Methodology

In order to minimize the effect of H, LAT and LON to the multi-temporal LST dataset a short of data transformation is required in order to produce a new set of images that should present high correlations to the three independent variables under consideration (Miliaresis 2012a). In this context, principal components analysis (PCA) is a linear transformation technique that produces a set of images known as principal components (PCs) that are uncorrelated with one another and are ordered in terms of the amount of variance (eigenvalues) they explain from the original image set (Jolliffe 2002). In previous research efforts (Miliaresis 2012a, b, c, 2013, 2014a) principal components analysis (PCA) is applied, by computing the eigenvalues and eigenvectors from the cross-correlation matrix of LST data. So, the resulting eigenvalues and eigenvectors correspond to the standardized LST data (each month presents mean equal to zero and standard deviation equal to 1). Then, PCs are computed from the linear combination of eigenvectors and the corresponding pixel values of the initial images (Mather and Koch 2011). Finally, linear regression models are applied to the first two PCs and spit the variance associated to H, LAT and LON that is included in the predicted images (Miliaresis 2012a, b, c).

ANOVA table for each regression verify the statistical significance (Miliaresis 2013, 2014a). The model performance is further assessed by the R² (R is the multiple correlation coefficient between the independent variables and the dependent variable) that represents the extent of variability in the dependent variable explained by all the independents variables (Landam and Everitt 2004). Then, the multi-temporal data set is reconstructed by considering the residual images for the first 2 PCs as well as the later PCs.

Study area

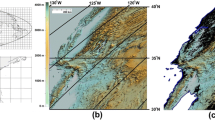
The study area (Fig. 1) is bounded by longitudes −124° to −112° (West) and latitudes 32° to 44° (North) and includes the states of California, Nevada, Utah and Arizona. NW of the study area (California), the climate is characterized by moderately cold winters with heavy snowfall on the mountains (Sierra Nevada Ranges) and warm, very dry summers with limited rainfall, especially in the south (Wang and Gillies 2012).

Fig. 1

Elevation map of the study area. The elevation values in the range (−83, 4092 m) were rescaled in the range 255 (white) to 0 (black). The lighter a pixel, the lower its elevation

The central and the eastern part of the study area (Nevada, Arizona and Utah) is mostly formed by a series of parallel mountain ranges intervening flat basins (Fig. 1). The climate is generally semi-arid or arid with warm summers and cold winters but this varies by location and elevation (Wang and Gillies 2012) since some mountainous areas are high enough in elevation to experience an Alpine climate. The majority of streams and rivers flow into desert sinks or closed-basin lakes while Colorado River crosses Grand Canyon in SE (Barnett and Pierce 2008). Southerly, the study area is occupied by Mojave Desert (California) and by Sonoran Desert (Arizona).

Data

The SRTM30 digital elevation model (DEM) (Farr and Kobrick 2000; SRTM30 DEM 2015) with spatial resolution equal to 0.00833 degrees (approximately 1 km at the equator) provides the elevation representation of the study area (Fig. 1). A geographic latitude/longitude grid is used with WGS 84 as horizontal datum (SRTM30 DOC 2015). The elevation range is in between −83 and 4097 m. Negative elevations (below sea level) are observed in Death Valley, (California).

Around local solar time 01:30, 10:30, 13:30 and 22:30 LST data are acquired from the MODIS instrument on board the Aqua and Terra polar orbiting satellite (MYD11C2 2011). The LST accuracy according to Wan (2014) is better than 1 K (0.5 K in most cases) under real clear-sky conditions. Data from real clear-sky conditions within a calendar month are averaged to yield the MYD11C2 for Aqua and MOD11C3 for Terra products (Wan 2013). MYD11C2 and MOD11C3 data sets provide a continuous (monthly averaged LST) sampling of the earth’s surface with a spatial resolution of 3 min (0.05° corresponding to 5.6 km approximately at the equator) referenced to a geographic latitude/longitude grid, with WGS 84 being the horizontal datum (Wan 2013).

A major improvement has been applied to the MODIS data products since a new processing algorithm is applied (Wan 2013) and the version 6 data products (Wan 2014) are gradually released to the public (MYD11C2.006 2016). The Aqua MODIS night (acquired daily on 01:30) monthly averaged LST data is used. The 12 night monthly averaged LST images for 2007 are visualized in Fig. 2. The monthly LST frequency distributions are presented in Fig. 3.

Fig. 2

The monthly averaged night LST imagery of the study area for the year 2007. Each image is rescaled to it’s minimum (black) and it’s maximum (white) in attempt reveal negative (black pixels) and positive (white pixels) LST outliers

Fig. 3

The frequency distribution per LST image. A common LST value range [−20, 32 °C] is used in order to reveal the seasonal shifting of distributions through out the 2007

The data might be also represented by the cross correlation matrix in Table 1 that indicates a rather season dependent correlation of LST with H, LAT and LON.

Table 1 Cross correlation matrix

Density slicing of the November LST image is presented in Fig. 4. The one slice includes the pixels with LST <0 °C while the coastal regions include the pixels with LST >0 °C.

Fig. 4

Density slicing of the November LST image reveals the H, LAT, LON dependency of LST. a The elevation map of the study area (the lighter a pixel the greater its elevation) is overlaid to the region formed by pixels with negative LST. b The elevation map of the study area is overlaid to the region formed by pixels with positive LST

SVR software implementation

SVR is a modular, flexible, open-source GNU Octave 4.0 script for selective variance reduction of multi-temporal data sets. The SVR script, the supporting functions, the visualization scripts as well as the study area data are freely available under GNU Version 3 General Public License. A website has been set-up to facilitate the distribution (https://sourceforge.net/projects/selective-variance-reduction/). Various scripts and functions are included that allow alternative processing options and visualizations.

There are 48,224 data (land) pixels in the study area. The data files are stored in a single Matlab file, under the name california.mat that includes 4 matrices. The vector representation is selected, and so each data element (vector) includes the 12 monthly LST values of a specific pixel. Thus, there are 48,224 vectors (rows) in the LST matrix and 12 columns corresponding to the monthly averaged night LST from January to December 2007. The LST vectors are visualized in Fig. 5. There are 3 more one-dimensional matrices, named H, LAT and LON that correspond to the elevation, latitude and longitude per vector (pixel).

Fig. 5

Visualization of the LST vectors. X-axis indicate the month [J, F, M, A, M, J, J, A, S, O, N, D], Y-axis indicate the vector ID in the range [1, 48,224], while Z axis corresponds to LST in degree Celsius

The main script is termed SVR.m (Table 2). SVR is an acronym for selective variance reduction, indicating that the variance associated to H, LAT and LON is subtracted from the multi-temporal LST data.

Table 2 SVR.m script

There are two function-calls in SVR script (Table 2):

• a. PCAfunc.m (Table 3) that computes the eigenvalues and eigenvectors from the variance covariance matrix of LST, and

  Table 3 PCAfunc.m and normal_equation.m scripts

• b. Normal_equation.m (Table 3) that performs the linear regressions of PC1 and PC2 versus H, LAT and LON and computes the two residual images that are used in LST image reconstruction.

The Eig function (Table 3) uses the variance–covariance matrix for the computation of PCs (Eig 2015), thus the reconstructed LST imagery should express thermal anomalies in degrees Celsius. Translation by mean is applied before Eig function is applied (Table 3) in an attempt to improve the accuracy of numerical computations. Translation by mean of the LST variables (instead of using the raw monthly data), use the difference between the variables (monthly averaged LST) and their sample means. Translation does not affect the interpretation because the variances of the original variables are the same as those of the translated variables.

The eigenvectors returned by Eig function (Eig 2015) of OCTAVE are not ordered. That is why in PCAfunc.m (Table 3), the eigenvectors are sorted in a descending variance (eigenvalue) order. The PCs for the LST data of the study area are presented in Table 4.

Table 4 Eigenvectors, eigenvalues and principal components (PCs) of the multi-temporal LST data

In SVR.m script (Table 2), the PCs (Table 4) are computed from the linear combination of eigenvectors and the corresponding pixel values of the initial images.

The contribution of the independent variables (H, LAT, LON) to PC1 and PC2 (dependent variables) is quantified by the linear regression models in Eqs. (1) and (2).

$${\text{PC1}} = 1 3 5. 8 5 1 9 8 - 0.0 1 1 7 5 8\times {\text{H}} - 3. 3 9 3 3 2\times {\text{LAT}} - 0. 2 20 6 7\times {\text{LON}}$$

(1)

$${\text{PC2}} = -1 8 6. 8 8 2 3 + 0.000 4 80 7 9\times {\text{H}} - 0. 3 60 2 3 2\times {\text{LAT}} -1. 4 7 7 1 7\times {\text{LON}}$$

(2)

The R² (Table 5) indicates the amount of variance explain by the multiple lineal regression models (Landam and Everitt 2004).

Table 5 ANOVA tables for Eqs. (1 )and (2) (df degrees of freedom)

The analysis of variance (ANOVA) tables for Eqs. (1) and (2) are presented in Table 5. The F-statistic and the t-statistic (Landam and Everitt 2004) combined are used in estimating, (a) the success of the regression models and (b) for adding or deleting variables (the significance of independent variables) respectively. The F-test value for Eq. (1) indicates the overall significance of the regression, since it far exceeds the F-critical value (26.12) at the 0.01 significance level (Table 5). For Eq. (1), the coefficients for H, LAT and LON (Table 5) express the individual contribution of the independent variable to PC1. The absolute values of the t test for the 3 independent variables (Table 5) far exceed the t-critical value (2.58) at two tailed 0.01 significance level and hence their coefficients depart significantly from 0.

The ANOVA table (Table 5) for Eq. (2) also verifies the overall significance of the multiple regression model for PC2, as well as the significance of the 3 independent variables.

The SVR.m script reconstruct the PC scores (Scores 2) in Table 2, by considering the regression residuals of PC1 and PC2 plus the PC3 to PC12 components. Then the inverse transformation (Table 2) computes the reconstructed LST (RLST) images from the multiplication of Scores2 matrix times the transpose matrix of eigenvectors (Table 4).

The 12 night monthly averaged reconstructed LST (RLST) images for 2007 are visualized in Fig. 6. The RLST frequency distribution per month are presented in Fig. 7 while the RLST vectors are presented in Fig. 8. Descriptive statistics (Landam and Everitt 2004) for the RLST frequency distributions are available in Table 6.

Fig. 6

The monthly averaged RLST (thermal anomaly) imagery of the study area for the year 2007 indicating the deviation per pixel in degrees Celsius, from the elevation, latitude, longitude predicted LST. Each image is rescaled to it’s minimum (black) and it’s maximum (white) in attempt reveal negative (black pixels) and positive (white pixels) RLST outliers

Fig. 7

The frequency distribution per RLST image. A common RLST value range [−12, 12 °C] is used

Fig. 8

Visualization of the RLST vectors. X-axis indicate the month [J, F, M, A, M, J, J, A, S, O, N, D], Y-axis indicate the vector ID in the range [1, 48,224], while Z axis corresponds to RLST (thermal anomaly) in degree Celsius

Table 6 RLST descriptive statistics (thermal anomaly in degree Celsius)

Discussion of results

Table 1 indicates a season dependent correlation in between H, LAT, LON and LST as well as that LST decreases with increasing LAT and H.

If a different function (not the Eig 2015) is used for the computation of eigenvectors (Table 3), then some or all of the PCs columns in Table 4 might have opposite signs. This is ok, since there is no “natural” orientation for PCs (Jolliffe 2002; Mather and Koch 2011). So, the PCs axes pointing has no implication to SVR computation. The key issue of Eig function is that the eigenvectors are computed from variance–covariance matrix and not from the correlation matrix (Table 1). That is why, the RLST imagery express thermal anomalies in degrees Celsius (Figs. 6, 7). So in the current implementation, RLST per pixel expresses the LST deviation from the elevation, latitude, longitude predicted LST in degrees Celsius.

On the contrary, if the correlation matrix is used then the standardized thermal anomalies will be presented in each reconstructed LST image (Miliaresis 2012a, b, c, 2013, 2014a). Thus, LST thermal anomalies for every pixel will be in the range [−1, 1]. These values are either positive or negative depending on the normal scores per month of the multi-temporal dataset. Under these circumstances (Miliaresis 2012a, b, c, 2013, 2014a) there is not a direct correspondence in between RLST values and both the magnitude and the sign (positive or negative) of the thermal anomalies.

The first 2 PCs accounts for the 97.4 % of the variance evident within the multi-temporal imagery (Table 4) while PC-3 to PC-12 components account only for the 2.6 % of the total variance evident in the initial data. The Eqs. (1) and (2) explain 76.12 % of the total variance evident in the multi-temporal LST data. More specifically:

• For Eq. (1), R² equals to 0.802 (Table 5). Thus, according to the PC1 eigenvalue (percent variance of PC1 equals to 88.38 % in Table 4), the 70.8 % (0.802 × 88.38 %) of the total variance of the LST data is explained by Eq. (1).

• For Eq. (2), R² equals to 0.601 (Table 5). Thus, according to the PC2 eigenvalue (the percent variance of PC2 equals to 9.02 % in Table 4), the 5.42 % (0.601 × 9.02 %) of the total variance of the LST data is explained by Eq. (2).

Thus, the two residual images for Eqs. (1) and (2) accounts for the 17.58 % (88.38–70.8) and 3.6 % (9.02–5.42) respectively, of the total variance evident in the multi-temporal dataset. So the RLST imagery (Fig. 3) accounts only for the 23.78 % (17.58 + 3.6 + 2.6 %) of the total variance of the initial data that is independent of H, LAT and LON.

The LST frequency distributions (Fig. 3) are bi-modal. Density slicing of the November LST image (Fig. 4) outlines two regions, (a) the coastal one with positive LST and elevation statistics equal to 885 ± 654 m and (b) a continental one with negative LST and elevation statistics equal to 1809 ± 476 m. So H, LAT and LON do play a major role in the observed values of LST. On the contrary, the RLST frequency distributions (Fig. 7) present means that approach zero (Table 6).

According to an empirical rule (Daniel and Tennant 2001), when the absolute value of the skew exceeds a value, such as 0.5, then the distribution is sufficiently asymmetrical to cause concern that the dataset may not represent a normal distribution. In the current case study (Fig. 7) the RLST distributions present absolute value of skew that is far less than 0.5 (Table 6).

Kurtosis characterizes the relative peakedness or flatness of a distribution compared with the normal distribution (Landam and Everitt 2004). A value of 0 represents a mesokurtic curve, more particularly, the bell-shaped curve of the normal distribution (Daniel and Tennant 2001). Positive kurtosis indicates a relatively peaked (leptokurtic) distribution (Miliaresis and Paraschou 2005). The frequency distributions of July and August are rather leptokurtic ones since they do present kurtosis greater than 0.7 (Table 6). So RLST values are distributed more around the mean value for July and August. It is concluded that the regional increase of LST during the summer masks the regions of high thermal anomaly (positive or negative) and attenuates their difference from the surrounding land.

Thresholding of either very high (positive thermal anomaly) or very low (negative thermal anomaly) RSLT values (Fig. 6) on the basis of RSLT histogram frequency distributions (Fig. 7) can map the spatial distribution of the thermal anomaly pattern for each month.

Lets compare the vector visualizations for LST (Fig. 5) versus RLST data (Fig. 8). LST vectors presents a gradual increase of LST from January to July, followed by a gradual decrease in LST (Fig. 5). On the contrary RLST vectors present a residual bending (negative RLST anomaly) in Spring. The bending is verified by the negative mean values of RLST in Table 6. Table 6 also verifies that the bending is maximized in April. A tentative hypothesis is that snow melting and the associated water table depth fluctuation might be responsible for the seasonal bending of vectors. The geomorphology of the study area (elevated mountain ranges intervening desert basins) and the snowfall seasonal pattern (Wang and Gillies 2012) support this hypothesis. Miliaresis (2014a, b) observed a rather similar (in concept) LST pattern in Antarctica, that it was related to ice surface melting during the long Antarctic day (summer). Nevertheless, seasonal winds and air circulation pattern might also be responsible for the negative thermal anomaly bending.

Conclusion

The Selective Variance Reduction script took advantage of the Eig function of Octave 4.0 software that determines the eigenvectors and eigenvalues from the variance–covariance matrix. Thus, it is possible to apply elevation, latitude longitude decorrelation stretch of multitemporal monthly averaged night LST imagery for 2007 in SW USA, in attempt to quantify thermal anomalies in degrees Celsius. For each reconstructed LST imagery, the thermal anomaly value (RLST) per pixel expresses the LST deviation in degrees Celsius, from the elevation, latitude, longitude predicted LST. Under these circumstances, there is a direct correspondence in between the reconstructed LST values and both the magnitude and the sign (positive or negative) of thermal anomalies.