Skip to main content
SpringerLink
Log in

Functionally Graded Porous Conical Nanoshell Buckling during Axial Compression Using MCST and FSDT Theories by DQ Method

  • S.I.: Computations & Experiments on Dynamics of Complex Fluid & Structure
  • Published:
Experimental Techniques Aims and scope Submit manuscript

Abstract

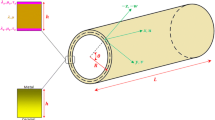
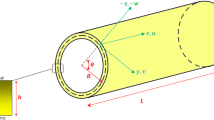
Buckling analysis of functionally graded porous nano conical shell subjected to axial compression is studied in this paper. The porous material properties vary across the thickness by a special function. First order shear deformation theory and modified couple stress theory are used to obtain the governing equation. Shells` nonlinear equilibrium and linear stability equations are obtained by Euler’s relations and Treftz principles. To solve the stability equations, the differential quadrature method (DQM) is used. The accuracy and the reliability of this paper are compared with reported studies. Finally, the effect of shell’s porous parameters, boundary condition, vertex angle and length scale on the amount of critical buckling force is discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Charlier J-C, Rignanese G-M (2001) Electronic structure of carbon nanocones. Phys Rev Lett 86(26):5970

    Article  CAS  Google Scholar 

  2. Hadavand BS, Javid KM, Gharagozlou M (2013) Mechanical properties of multi-walled carbon nanotube/epoxy polysulfide nanocomposite. Mater Des 50:62–67

    Article  Google Scholar 

  3. Knaapila M et al (2011) Conductivity enhancement in carbon nanocone adhesive by electric field induced formation of aligned assemblies. ACS Appl Mater Interfaces 3(2):378–384

    Article  CAS  Google Scholar 

  4. Shenderova O et al (2001) Predicted structure and electronic properties of individual carbon nanocones and nanostructures assembled from nanocones. Nanotechnology 12(3):191

    Article  CAS  Google Scholar 

  5. Mylvaganam K, Zhang L (2004) Important issues in a molecular dynamics simulation for characterising the mechanical properties of carbon nanotubes. Carbon 42(10):2025–2032

    Article  CAS  Google Scholar 

  6. Shibuta Y, Maruyama S (2003) Molecular dynamics simulation of formation process of single-walled carbon nanotubes by CCVD method. Chem Phys Lett 382(3–4):381–386

    Article  CAS  Google Scholar 

  7. Zhou L, Shi S (2002) Molecular dynamic simulations on tensile mechanical properties of single-walled carbon nanotubes with and without hydrogen storage. Comput Mater Sci 23(1–4):166–174

    Article  CAS  Google Scholar 

  8. Van Dung D (2017) Analytical investigation on mechanical buckling of FGM truncated conical shells reinforced by orthogonal stiffeners based on FSDT. Compos Struct 159:827–841

    Article  Google Scholar 

  9. Sofiyev A, Zerin Z, Kuruoglu N (2017) Thermoelastic buckling of FGM conical shells under non-linear temperature rise in the framework of the shear deformation theory. Compos Part B: Eng 108:279–290

    Article  Google Scholar 

  10. Civalek Ö (2017) Buckling analysis of composite panels and shells with different material properties by discrete singular convolution (DSC) method. Compos Struct 161:93–110

    Article  Google Scholar 

  11. Van Dung D, Dong DT (2016) Post-buckling analysis of functionally graded doubly curved shallow shells reinforced by FGM stiffeners with temperature-dependent material and stiffener properties based on TSDT. Mech Res Commun 78:28–41

    Article  Google Scholar 

  12. Sofiyev A (2016) Thermoelastic stability of freely supported functionally graded conical shells within the shear deformation theory. Compos Struct 152:74–84

    Article  Google Scholar 

  13. Sofiyev A (2016) Buckling of heterogeneous orthotropic composite conical shells under external pressures within the shear deformation theory. Compos Part B: Eng 84:175–187

    Article  Google Scholar 

  14. Mehri M, Asadi H, Wang Q (2016) Buckling and vibration analysis of a pressurized CNT reinforced functionally graded truncated conical shell under an axial compression using HDQ method. Comput Methods Appl Mech Eng 303:75–100

    Article  Google Scholar 

  15. Jooybar N et al (2016) Thermal effect on free vibration of functionally graded truncated conical shell panels. Thin-Walled Struct 103:45–61

    Article  Google Scholar 

  16. Jabbari M, Nejad MZ, Ghannad M (2016) Thermo-elastic analysis of axially functionally graded rotating thick truncated conical shells with varying thickness. Compos Part B: Eng 96:20–34

    Article  Google Scholar 

  17. Demir Ç, Mercan K, Civalek Ö (2016) Determination of critical buckling loads of isotropic, FGM and laminated truncated conical panel. Compos Part B: Eng 94:1–10

    Article  Google Scholar 

  18. Ansari R, Torabi J (2016) Numerical study on the buckling and vibration of functionally graded carbon nanotube-reinforced composite conical shells under axial loading. Compos Part B: Eng 95:196–208

    Article  CAS  Google Scholar 

  19. Sofiyev A, Kuruoglu N (2015) On the solution of the buckling problem of functionally graded truncated conical shells with mixed boundary conditions. Compos Struct 123:282–291

    Article  Google Scholar 

  20. Sofiyev A (2015) On the vibration and stability of shear deformable FGM truncated conical shells subjected to an axial load. Compos Part B: Eng 80:53–62

    Article  Google Scholar 

  21. Sofiyev A (2015) Buckling analysis of freely-supported functionally graded truncated conical shells under external pressures. Compos Struct 132:746–758

    Article  Google Scholar 

  22. Kitipornchai S, Chen D, Yang J (2017) Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mater Des 116:656–665

    Article  CAS  Google Scholar 

  23. Magnucki K, Stasiewicz P (2004) Elastic buckling of a porous beam. J Theor Appl Mech 42(4):859–868

    Google Scholar 

  24. Allahkarami F, Saryazdi MG, Tohidi H (2020) Dynamic buckling analysis of bi-directional functionally graded porous truncated conical shell with different boundary conditions. Compos Struct 252:112680

    Article  Google Scholar 

  25. Das A, Rout M, Karmakar A (2020) Time dependent response of impact induced functionally graded conical shell considering porosity. Sādhanā 45(1):1–15

    Article  Google Scholar 

  26. Shahgholian D et al (2020) Buckling analyses of functionally graded graphene-reinforced porous cylindrical shell using the Rayleigh–Ritz method. Acta Mech:1–16

  27. Yuan Y et al (2020) Couple stress-based nonlinear buckling analysis of hydrostatic pressurized functionally graded composite conical microshells. Mech Mater 148:103507

    Article  Google Scholar 

  28. Ansari R, Torabi J, Hasrati E (2020) Postbuckling analysis of axially-loaded functionally graded GPL-reinforced composite conical shells. Thin-Walled Struct 148:106594

    Article  Google Scholar 

  29. Salmani R et al (2021) Analytical investigation on the nonlinear postbuckling of functionally graded porous cylindrical shells reinforced with graphene nanoplatelets. Euro Phys J Plus 136(1):1–19

    Article  Google Scholar 

  30. Shahgholian-Ghahfarokhi D, Safarpour M, Rahimi A (2021) Torsional buckling analyses of functionally graded porous nanocomposite cylindrical shells reinforced with graphene platelets (GPLs). Mech Based Des Struct Mach 49(1):81–102

    Article  Google Scholar 

  31. Heidari Y, Arefi M, Irani-Rahaghi M (2021) Free vibration analysis of cylindrical micro/nano-shell reinforced with CNTRC patches. Int J Appl Mech:2150040

  32. Sofiyev AH et al (2020) Buckling behavior of FG-CNT reinforced composite conical shells subjected to a combined loading. Nanomaterials 10(3):419

    Article  CAS  Google Scholar 

  33. Xiaolin H et al (2021) Vibration analysis of functionally graded porous conical shells rested on elastic foundations1. Mech Eng 43(4):536

    Google Scholar 

  34. Yang F et al (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39(10):2731–2743

    Article  Google Scholar 

  35. Eringen AC (1980) Mechanics of continua. Robert E. Krieger Publishing Co, Huntington, p 606

    Google Scholar 

  36. Tadi Beni Y (2016) F. Mehralian, and H. Zeighampour, the modified couple stress functionally graded cylindrical thin shell formulation. Mech Adv Mater Struct 23(7):791–801

    Article  Google Scholar 

  37. Bert CW, Malik M (1996) Differential quadrature method in computational mechanics: a review

  38. Li J-J, Cheng C-J (2005) Differential quadrature method for nonlinear vibration of orthotropic plates with finite deformation and transverse shear effect. J Sound Vib 281(1–2):295–309

    Article  Google Scholar 

  39. Tong L, Wang TK (1992) Simple solutions for buckling of laminated conical shells. Int J Mech Sci 34(2):93–111

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Islamic Azad University, Arak Branch, Arak, Iran

    M. Gheisari, A. Nezamabadi, M.M. Najafzadeh, S. Jafari & P. Yousefi

Authors
  1. M. Gheisari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Nezamabadi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M.M. Najafzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. S. Jafari
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. P. Yousefi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Nezamabadi.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gheisari, M., Nezamabadi, A., Najafzadeh, M. et al. Functionally Graded Porous Conical Nanoshell Buckling during Axial Compression Using MCST and FSDT Theories by DQ Method. Exp Tech 47, 313–326 (2023). https://doi.org/10.1007/s40799-021-00541-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40799-021-00541-6

Keywords

Search

Navigation