1 Introduction

Traffic congestion and emissions are two major negative externalities of the transportation system. Over decades, many traffic flow management strategies such as road pricing (Yin and Lawphongpanich 2006; Xu et al. 2016; Zhong et al. 2020) and tradable credit scheme (Wang et al. 2012; Gao and Sun 2014) have been designed to mitigate or internalize these externalities to improve the urban logistics efficiency and social welfare. For example, in light of the potential inconsistency between reducing congestion and reducing emissions (Nagurney 2000), Chen and Yang (2012) developed Pareto-efficient toll and rebate scheme to simultaneously minimize the congestion and emission.

In recent years, connected autonomous vehicles (CAVs) have caught great attention from the public and transportation planners due to their capability of enhancing traffic safety (Wadud 2017; Fagnant and Kockelman 2015), reducing fuel consumption (Barth and Boriboonsomsin 2009; Wadud et al. 2016), and increasing road capacity (Tientrakool et al. 2011) and driver productivity (Noruzoliaee et al. 2018), etc. Though it is tempting to replace regular vehicles (RVs) on the road with CAVs, we can envision that the road traffic will be mixed with RVs and CAVs for a long time. By leveraging the CAV flow in the mixed flow, researchers have developed a variety of new approaches for the congestion and emission management. Generally, these strategies mainly hinge on: (a) the control of CAVs’ speed profile or trajectory (Wang 2018; Yao et al. 2020; Xiong and Jiang 2021), (b) the control of CAVs’ routing behavior (Chen et al. 2020; Zhang and Nie 2018; Li et al. 2018; Sharon et al. 2018), and (c) the deployment of CAV-related infrastructure (Chen et al. 2016, 2017; Li et al. 2020; Liu et al. 2021). Specifically, controlling CAVs’ velocity, acceleration, and deceleration can achieve goals such as fuel consumption reduction (Yao et al. 2020; Xiong and Jiang 2021) and traffic flow stabilization (Wang 2018). For example, jointly optimizing traffic signal timing plans and CAVs’ trajectory can reduce the fuel consumption and CO\(_2\) emissions by 22.36% and 18.61%, respectively, in a network fully penetrated with CAVs (Yao et al. 2020). Regarding the routing behavior, CAVs’ route choices are assumed to be controllable due to their self-driving feature. Given this, Chen et al. (2020) proposed a path-control scheme to achieve the system optimum (SO), i.e., the minimum of total traffic delay, by controlling a portion of CAVs to follow the SO routing principle. It is found that the control ratio of CAVs can be very low with the implementation of the pricing scheme. The presence of CAV dedicated infrastructure, such as CAV lanes, CAV zones, and roadside units (RSUs), may affect the travel behavior of CAVs and thus the whole traffic flow, so optimizing these CAV dedicated infrastructure deployment plan can yield a reduction of traffic congestion and emissions. For example, Chen et al. (2017) optimized the deployment plan of CAV zones in a network with both RVs and CAVs to substantially reduce the social cost.

Inspired by the spirit of Chen et al. (2017), this paper aims to optimally deploy RSUs in a way to mitigate network congestion and emissions. RSUs are devices installed by the roadside to sense vehicles within their coverage areas, collect the motion information of these vehicles and communicate the collected data with CAVs on the road and the traffic management agence. In particular, RSUs can provide CAVs with information about the road traffic condition to improve their decision making in terms of choices of routes and driving profiles (Xie and Liu 2022; RGBSI 2021). Without a doubt, different RSU deployment plans may provide information with different qualities. For example, denser deployment of RSUs can collect more data, thereby offering a more comprehensive picture of the traffic on the network and enabling more reliable and robust communication; while sparse deployment implies the opposite. The information quality is expected to impact the path choice of CAV users (Chen and Du 2017; Spana et al. 2021), given that the information of higher quality is more likely to guide drivers to the fast paths and save them travel time and energy consumption (Xie and Liu 2022). As a result, this will further affect the long-term expected cost of using CAVs, which consequently impacts their adoption rate. In the meantime, the change of CAV penetration will in return influence the information quality because CAVs can also collect data in its neighborhood and share it with peer CAVs and RSUs (Xie and Liu 2022).

In this paper, RSUs will be deployed on a network where travelers make both long-term, i.e., vehicle type choice, and short-term, i.e., route choice, decisions, according to stochastic user equilibrium (SUE) principle. The information quality of CAVs is mediated by the RSU deployment plan and endogenous CAV penetration. Specifically, the impact of information quality on CAV users’ route choice is captured through the variable dispersion parameter in the path choice SUE model (Yang 1998; Lo and Szeto 2002; Yin and Yang 2003; Xie and Liu 2022), which reflects the fact that information of higher quality can increase the probability of choosing fast paths by lowering the travel time perception error. As such, different RSU deployment plans may yield different network flow distributions corresponding to different levels of network delay and emissions. Therefore, it is of critical importance to optimally design the RSU deployment plan to stimulate the change of routing behaviors of CAVs and their adoption rate in a way to mitigate the traffic congestion and emissions. To this end, we adopt the structure of Stackelberg game for the RSU optimization. Specifically, government agencies serve as the leader to design the deployment plan of RSUs, while travelers are the followers to make spontaneous reaction in terms of their choices of routes and vehicle types. Mathematically, the deployment problem can be formulated as an optimization program with equilibrium constraints (MPEC). An active-set algorithm is proposed to solve the MPEC. To the best of our knowledge, we are one of the first to explore the possibility of leveraging the RSU deployment to affect both the routing behavior of CAVs and their market penetration in a way to mitigate traffic congestion and emissions. Since the deployment of RSUs can be well combined with existing highway infrastructures, it can serve as a flexible instrument for congestion and emission management. The model and algorithm developed in this paper can be readily used to examine potential effect of a specific RSU deployment plan or to provide practical guidance to RSU deployment projects.

The remainder of this paper is organized as follows. In Sect. 2, we establish the network equilibrium model with mixed traffic flow and the optimization program for the RSU deployment. Section 3 presents the active-set algorithm to solve the optimization problem, followed by numerical experiments in Sect. 4. Finally, Sect. 5 concludes the paper and points out potential extensions to our work.

2 Model formulation

Consider a connected network G(V, A) where V and A are the sets of nodes and links, respectively. The set of origin-destination (OD) pairs is denoted by W. For any given OD pair \(w\in W\), the travel demand \(Q^w\) is assumed fixed and deterministic, and the feasible path set is denoted by \(K^w\). Travelers may choose to purchase either a CAV or RV based on their expected travel cost or utility. We define set \(I = \{{\text{CAV}}, {\text{RV}}\}\) as the vehicle type set. Therefore, the traffic flow on the network is mixed with CAVs and RVs. Let \(f_i^k\) be the flow on path \(k\in K^w\ (w\in W)\) of vehicle type \(i\in I\) and \(x_{ia}\) the flow on link \(a\in A\) of vehicle type \(i\in I\). Then we have \(x_{ia} = \sum _{w\in W}\sum _{k\in K^w}\delta _a^kf_{i}^k\), where \(\delta _a^k\) is the path-link incidence. The expected travel time on link \(a\in A\), denoted by \(t_a\), is a strictly increasing function in the link flow \(x_a = \sum _{i\in I}x_{ia}\), i.e., \(t_a = t_a(x_a)\) and \(\text{d}t_a/\text{d}x_a>0\). The expected travel time on path k is thus given by \(T^k = \sum _{a\in A}\delta ^k_at_a\).

2.1 Stochastic user equilibrium

A logit-based stochastic user equilibrium (SUE) model will be established in this section to capture the vehicle type choices and path choices made by travelers. Travelers’ path choices are informed by both CAV penetration and the deployment plan of RSUs on the network, which in return affects the expected travel costs of CAVs and RVs. We will first establish the path choice equilibrium with a given CAV penetration rate, based on which we proceed to develop the vehicle type choice model. Table 1 presents the notation used in our methodology.

Table 1 List of notations
Full size table

2.1.1 Path choice equilibrium

For any given OD pair \(w\in W\), let \(q_i^w\) be the number of travelers whose vehicle type choice is \(i\in I\), and \(f_i^{wk}\) the number of them who choose path \(k\in K^w\). At SUE, no traveler can reduce his/her perceived travel time by unilaterally changing his/her path choice. According to Sheffi (1984), the path choice SUE is characterized by

$$\begin{aligned} f_i^{wk} = P_i^{wk}q^w_i, \forall k \in K^w, w\in W, i\in I \end{aligned}$$
(1)

where \(P^{wk}_i\), defined as the probability of choosing path k for travelers with OD \(w\in W\) and vehicle type choice \(i\in I\), is given by the logit-based choice probability

$$\begin{aligned} P_i^{wk} = \frac{\exp {(-\theta ^w_iT^k)}}{\sum _{r\in K^w}\exp {(-\theta ^w_iT^r)}}, \forall k\in K^w, w\in W, i\in I \end{aligned}$$
(2)

Note that the value of the dispersion parameter for CAV users \(\theta ^w_{\text{CAV}}\) decreases in the number of RSUs on the paths in \(K^w\) as well as the CAV penetration (i.e., \(q^w_{\text{CAV}}/Q^w\)), because the more RSUs and higher penetration of CAVs on the paths in \(K^w\), the more accurate information about the travel time of these paths will be collected and shared with the CAV users, and they are thus more likely to choose the path with minimum expected travel time.

Let \(n_a\) be the number of RSUs deployed on link \(a\in A\). The density of RSUs deployed on path \(k\in K^w\) is defined as the total number of RSUs deployed on path k divided by the path length, i.e., \(\rho ^k = \frac{\sum _{a\in A}\delta ^k_a n_a}{\sum _{a\in A}\delta ^k_a l_a}, k\in K^w\), where \(l_a\) is the length of link \(a\in A\). The implication here is that with a higher RSU density, there are more devices collecting and sending data per unit length of the link, thereby enabling more robust and reliable V2I communication and improving the information quality for CAV users. Without loss of generality, the dispersion parameter \(\theta ^w_{\text{CAV}}\) for CAV users with OD pair w is defined as a strictly increasing function in the RSU density on the paths belonging to \(K^w\) and the CAV penetration:

$$\begin{aligned} \theta ^w_{\text{CAV}} = g_{\theta }(\varvec{\rho }^w, q^w_{\text{CAV}}), \forall w\in W \end{aligned}$$
(3)

where \(\varvec{\rho }^w = \{\rho ^k:k\in K^w\}\) is the vector of the numbers of RSUs on the paths in \(K^w\).

We now propose an alternative condition for the path choice equilibrium. This condition, together with the one for vehicle type choice equilibrium (see Proposition 2 in Sect. 2.1.2), will facilitate the proposition of an equivalent variational inequality (VI) problem which can be easily solved.

Proposition 1

Given a RSU deployment plan \({\textbf {n}} = \{n_a: a\in A\}\), a feasible path flow pattern \({\textbf {f}}\in \Omega _{{\textbf {f}}}= \{{\textbf {f}}\ge 0:\sum _{k\in K^w}f^{wk}_i = q^w_i, \forall w\in W, i \in I\}\) is at equilibrium if and only if it satisfies

$$\begin{aligned} \theta ^w_iT^k + \ln {f^{wk}_i} = \mu ^w_i, \forall k \in K^w, w\in W, i\in I \end{aligned}$$
(4)

where \(\mu ^w_i = \ln {\frac{q^w_i}{\sum _{r\in K^w}\exp (-\theta ^w_iT^r)}},\forall w\in W, i\in I\).

Proof

We first prove the sufficiency of the proposition. Given a feasible path flow pattern \({\textbf {f}}\in \Omega _{{\textbf {f}}}\) such that condition (4) is satisfied, and the definition of \(\mu ^w_i\), we have

$$\begin{aligned}f^{wk}_i &= \exp (\mu ^w_i)\exp (-\theta ^w_i T^k), \\&\quad \forall k \in K^w, w\in W, i \in I \end{aligned}$$
(5)
$$\begin{aligned}&q^w_i = \sum _{r\in K^w} f^{wr}_i = \exp (\mu ^w_i)\sum _{r\in K^w}\exp (-\theta ^w_i T^r), \\&\forall w\in W, i \in I \end{aligned}$$
(6)

Dividing Eq. (5) by Eq. (6), we have

$$\begin{aligned} \frac{f^{wk}_i}{q^w_i} = \frac{\exp (-\theta ^w_i T^k)}{\sum _{r\in K^w}\exp (-\theta ^w_i T^r)} \end{aligned}$$
(7)

which is identical to the equilibrium conditions (1) and (2).

We then prove the necessity. Given a feasible path flow pattern \({\textbf {f}}\in \Omega _{{\textbf {f}}}\) at equilibrium (i.e., satisfying conditions (1) and (2)), we have

$$\begin{aligned} \begin{aligned} \theta ^w_i T^k + \ln (f^{wk}_i)&= \theta ^w_iT^k + \ln (P^{wk}_iq^w_i)\\&= \theta ^w_iT^k + \ln \left( \frac{\exp (-\theta ^w_i T^k)q^w_i}{\sum _{r\in K^w}\exp (-\theta ^w_i T^r)}\right) \\&= \ln {\frac{q^w_i}{\sum _{r\in K^w}\exp (-\theta ^w_iT^r)}}, \forall k \in K^w, w\in W, i\in I \end{aligned} \end{aligned}$$
(8)

which is exactly condition (4). \(\square\)

2.1.2 Vehicle type choice equilibrium

For any given OD pair \(w\in W\), let \(C^w_i\) be the long-term expected cost of using i-type vehicle, based on which travelers make their vehicle type choice. Clearly, \(C^w_i\) depends on the daily expected travel time on paths in \(K^w\), which is given by

$$\begin{aligned} \overline{T}^w_i = \sum _{k\in K^w} P^{wk}_iT^k,\ \forall w\in W, i\in I \end{aligned}$$
(9)

Here, we define \(C^w_i\) as an increasing function of \(\overline{T}^w_i\) which captures the impact of daily expected travel time on the long-term vehicle purchasing decision. Specifically,

$$\begin{aligned} C^w_i = g_C(\overline{T}^w_i) \end{aligned}$$
(10)

Then for travelers with OD \(w\in W\), the probability of choosing i-type vehicle is

$$\begin{aligned} P^{w}_i = \frac{\exp (-\theta C^w_i)}{\sum _{j\in I}\exp (-\theta C^w_j)}, \forall w\in W, i\in I \end{aligned}$$
(11)

The logit-based SUE condition for vehicle type choice is then given by

$$\begin{aligned} q^{w}_i = Q^wP^{w}_i, \forall w \in W, i \in I \end{aligned}$$
(12)

Similar to Proposition 1 in Sect. 2.1.1, we propose an equivalent condition for vehicle type choice equilibrium.

Proposition 2

Given a RSU deployment plan \({\textbf {n}} = \{n_a: a\in A\}\), a feasible vehicle type choice pattern \({\textbf {q}}\in \Omega _{{\textbf {q}}} = \{{\textbf {q}}\ge 0:\sum _{i\in I}q^{w}_i = Q^w, \forall w\in W\}\) is at equilibrium if and only if it satisfies

$$\begin{aligned} \theta C^w_i + \ln {q^{w}_i} = \lambda ^w, \forall w \in W \end{aligned}$$
(13)

where \(\lambda ^w = \ln {\frac{Q^w}{\sum _{j\in I}\exp (-\theta C^w_j)}},\forall w\in W\).

Proof

We first prove the sufficiency of the proposition. Given a feasible vehicle type choice pattern \({\textbf {q}}\in \Omega _{{\textbf {q}}}\) such that condition (13) is satisfied, and the definition of \(\lambda ^w\), we have

$$\begin{aligned} q^{w}_i= & {} \exp (\lambda ^w)\exp (-\theta C^w_i), \forall w\in W, i \in I \end{aligned}$$
(14)
$$\begin{aligned} Q^w= & {} \sum _{j\in I} q^w_j = \exp (\lambda ^w)\sum _{j\in I}\exp (-\theta C^w_j), \forall w\in W \end{aligned}$$
(15)

Dividing Eq. (14) by Eq. (15), we have

$$\begin{aligned} \frac{q^{w}_i}{Q^w} = \frac{\exp (-\theta C^w_i)}{\sum _{j\in I}\exp (-\theta C^w_j)} \end{aligned}$$
(16)

which is identical to the equilibrium conditions (11) and (12).

We then prove the necessity. Given a feasible vehicle type choice pattern \({\textbf {q}}\in \Omega _{{\textbf {q}}}\) at equilibrium (i.e., satisfying conditions (11) and (12)), we have

$$\begin{aligned} \begin{aligned} \theta C^w_i + \ln (q^{w}_i)&= \theta C^w_i + \ln (P^{w}_iQ^w)\\&= \theta C^w_i + \ln \left( \frac{\exp (-\theta C^w_i)Q^w}{\sum _{j\in I}\exp (-\theta C^w_j)}\right) \\&= \ln {\frac{Q^w}{\sum _{j\in I}\exp (-\theta C^w_j)}}, \forall w\in W, i\in I \end{aligned} \end{aligned}$$
(17)

which is exactly condition (13). \(\square\)

To guarantee the equilibrium of the whole system, the SUE conditions in Proposition 1 and Proposition 2 must be satisfied simultaneously.

2.1.3 Equivalent VI model

In this section, we reformulate the aforementioned equilibrium conditions into a variational inequality (VI) problem which is easy to solve. The VI of interest is defined as:

To find \(({\textbf {f}}^*,{\textbf {q}}^*)\in \Omega\), such that

$$\begin{aligned}&\sum _{i\in I}\sum _{w\in W}\sum _{k\in K^w} F^{wk}_i({\textbf {f}}^*,{\textbf {q}}^*)(f^{kw}_i-f^{wk*}_i) \\&\quad +\sum _{i\in I}\sum _{w\in W} G^w_i({\textbf {f}}^*,{\textbf {q}}^*)(q^w_i-q^{w*}_i)\ge 0, \forall ({\textbf {f}},{\textbf {q}})\in \Omega \end{aligned}$$
(18)

where

$$\begin{aligned}&F^{wk}_i({\textbf {f}}^*,{\textbf {q}}^*) = \theta ^w_iT^k + \ln {f^{wk}_i}, \\&\quad \forall k \in K^w, w\in W, i \in I \end{aligned}$$
(19)

and

$$\begin{aligned}&G^w_i({\textbf {f}}^*,{\textbf {q}}^*) = \theta C^w_i + \ln {\sum _{k\in K^w}\exp (-\theta ^w_iT^k)}, \\&\quad \forall w\in W, i\in I \end{aligned}$$
(20)

The feasible set \(\Omega\) is defined by

$$\begin{aligned}&\sum _{k\in K^w}f^{wk}_i = q^w_i, \forall w\in W, i \in I \end{aligned}$$
(21)
$$\begin{aligned}&\sum _{i\in I}q^{w}_i = Q^w, \forall w\in W \end{aligned}$$
(22)
$$\begin{aligned}&f^{wk}_i \ge 0, k\in K^w, w \in W, i\in I \end{aligned}$$
(23)
$$\begin{aligned}&q^w_i \ge 0, w\in W, i\in I \end{aligned}$$
(24)

Proposition 3

A joint path flow and vehicle type choice pattern \(({\textbf {f}}^*,{\textbf {q}}^*)\in \Omega\) satisfies equilibrium conditions (4) and (13) if and only if it solves the VI problem (18).

Proof

Let \(({\textbf {f}}^*,{\textbf {q}}^*)\) be a solution to the VI problem (18). Note that there are a few variables dependent on \(({\textbf {f}},{\textbf {q}})\), such as \(\theta ^w_i\) and \(T^k\), etc. For simplicity, we use asterisk to indicate their values at \(({\textbf {f}},{\textbf {q}}) = ({\textbf {f}}^*,{\textbf {q}}^*)\). For example, we use \(\theta ^{w*}_i\) to denote \(\theta ^w_i({\textbf {f}}^*,{\textbf {q}}^*)\).

Since \(({\textbf {f}}^*,{\textbf {q}}^*)\) solves VI problem (18), it must satisfies the optimality condition of the VI problem. That is, there exists a vector \((\varvec{\mu }^*,\varvec{\lambda }^*,\varvec{\sigma }^*,\varvec{\pi }^*)\) such that

$$\begin{aligned}&F^{wk}_i({\textbf {f}}^*,{\textbf {q}}^*) - \mu ^{w*}_i -\sigma ^{wk*}_i = 0, \\&\quad \forall k\in K^w, w\in W, i\in I \end{aligned}$$
(25)
$$\begin{aligned}&G^w_i({\textbf {f}}^*,{\textbf {q}}^*) + \mu ^{w*}_i - \lambda ^{w*}-\pi ^w_i = 0, \forall w\in W,i\in I \end{aligned}$$
(26)
$$\begin{aligned}&f^{wk*}_i\sigma ^{wk*}_i = 0, \forall k\in K^w, w\in W, i\in I \end{aligned}$$
(27)
$$\begin{aligned}&q^{w*}_i\pi ^{w*}_i = 0, \forall w\in W, i\in I \end{aligned}$$
(28)
$$\begin{aligned}&\sigma ^{wk*}_i\ge 0, \pi ^{w*}_i\ge 0, \forall k\in K^w, w\in W, i\in I \end{aligned}$$
(29)

Eqs. (21)–(24).

Note that if \(f^{wk}_i\) approaches to 0, then \(F^{wk}_i\) will approach to negative infinity, so (18) will not hold for all \(({\textbf {f,q}})\) and\(({\textbf {f}}^*,{\textbf {q}}^*)\in \Omega\). Therefore, we must have \(f^{wk}_i>0\). From (27), we have \(\sigma ^{wk*}_i=0\ (\forall k\in K^w, w\in W, i\in I)\). Using this and Eq. (25), we have

$$\begin{aligned}&f^{wk*} = \exp (\mu ^{w*}_i)\exp (-\theta ^{w*}_iT^{k*}), \\&\quad \forall k\in K^w, w\in W, i\in I \end{aligned}$$
(30)

By summing Eq. (30) over \(k\in K^w\) and using Eq. (21), we have

$$\begin{aligned}&q^{w*}_i = \sum _{k\in K^w} f^{wk*}_i = \exp (\mu ^{w*}_i)\sum _{k\in K^w}\exp (-\theta ^{w*}_iT^{k*}), \\&\quad \forall w\in W, i\in I \end{aligned}$$
(31)

From Eqs. (30) and (31), we immediately have the equilibrium flow pattern condition

$$\begin{aligned} \frac{f^{wk*}_i}{q^{w*}_i} = \frac{\exp (-\theta ^{w*}_i T^{k*})}{\sum _{r\in K^w}\exp (-\theta ^{w*}_i T^{r*})}, \forall w\in W, i\in I \end{aligned}$$
(32)

and the alternative expression for multipliers \(\mu ^{w*}_i\):

$$\begin{aligned} \mu ^{w*}_i = \ln {\frac{q^{w*}_i}{\sum _{r\in K^w}\exp (-\theta ^{w*}_i T^{r*})}}, \forall w\in W, i\in I \end{aligned}$$
(33)

which is identical with the condition in Proposition 1.

The condition for vehicle choice equilibrium can be derived in similar manner from the optimality condition of the VI problem. Since \(f^{wk}_i>0\), we must have \(q^w_i>0\). Using Eqs. (26), (28) and (33), we have

$$\begin{aligned} q^{w*}_i = \exp (\lambda ^{w*})\exp (-\theta C^{w*}_i), \forall w\in W, i \in I \end{aligned}$$
(34)

Summing Eq. (34) over \(i\in I\) and using Eq. (22), we have

$$\begin{aligned} Q^{w} = \sum _{i\in I}q^{w*}_i = \exp (\lambda ^{w*})\sum _{j\in I}\exp (-\theta C^{w*}_j), \forall w\in W \end{aligned}$$
(35)

From Eqs. (34) and (35), we have the vehicle type choice equilibrium condition and the alternative expression for multipliers \(\lambda ^{w*}\):

$$\begin{aligned} \frac{q^{w*}_i}{Q^w}= & {} \frac{\exp (-\theta C^{w*}_i)}{\sum _{j\in I}\exp (-\theta C^{w*}_j)}, \forall w\in W, i\in I \end{aligned}$$
(36)
$$\begin{aligned} \lambda ^{w*}= & {} \ln {\frac{Q^w}{\sum _{j\in I}\exp (-\theta C^{w*}_j)}},\forall w\in W \end{aligned}$$
(37)

which are identical to the condition in Proposition 2. Therefore, any \(({\textbf {f}}^*,{\textbf {q}}^*)\) that solves the VI problem (18) must satisfy both SUE conditions in Propositions 1 and 2.

Conversely, given an equilibrium path flow and vehicle type choice pattern \(({\textbf {f}}^*,{\textbf {q}}^*)\), we can find the optimal multipliers \(\mu _i^{w*}\) and \(\lambda ^{w*}\) using Eqs. (33) and (37). Since the optimality condition is both necessary and sufficient for VI problems with convex polyhedral feasible set (Facchinei and Pang 2003), \(({\textbf {f}}^*,{\textbf {q}}^*)\) is also a solution to VI problem (18). \(\square\)

2.2 RSU deployment model

The goal of the optimization model is to decide a RSU deployment plan to minimize the total network delay and emissions. To measure the emissions of the traffic flow, we adopt the following emission function based on average link speed (Wallace et al. 1984; Chen and Yang 2012; Yin and Lawphongpanich 2006):

$$\begin{aligned} e_{a}(x_a) = 0.2038t_a(x_a)\exp \left( \frac{0.7962l_a}{t_a(x_a)}\right) ,\forall a\in A \end{aligned}$$
(38)

where \(e_a(x_a)\) is the volume of CO emissions (g/veh) on link \(a\in A\) when the link flow is \(x_a\). \(l_a\) is the length (km) of link a and the link travel time \(t_a(x_a)\) is in the unit of km/min.

Now we consider the problem of minimizing the total network delay and the emissions by optimizing the deployment of RSUs on the network. Let \({\textbf {n}}=\{n_a:\forall a\in A\}\) be the RSU deployment plan. It parameterizes the mixed flow traffic equilibrium and its equivalent VI problem (18). For any given RSU deployment plan \({\textbf {n}}\), let \(SOL(\Omega ,{\textbf {F(n)}},{\textbf {G(n)}})\) denote the solution set of VI problem (18). The optimization problem for mitigating delay and emissions via RSU deployment (named by RSUD) is then defined as a mathematical program with equilibrium constraints (MPEC):

$$\begin{aligned}&\text {(RSUD)}\ \min _{{\textbf {n}}}\ \gamma _1\sum _{a\in A} t_a(x_a)x_a + \gamma _2\sum _{a\in A} e_a(x_a)x_a \end{aligned}$$
(39)
$$\begin{aligned}&s.t.\ \sum _{a\in A} n_a \le N \end{aligned}$$
(40)
$$\begin{aligned}&\underline{n}_a\le n_a \le \bar{n}_a, \forall a\in A \end{aligned}$$
(41)
$$\begin{aligned}&x_a = \sum _{i\in I}\sum _{w\in W}\sum _{k\in K^w} \delta ^k_af^{wk}_i, \forall a\in A \end{aligned}$$
(42)
$$\begin{aligned}&n_a\in Z_+, \forall a\in A \end{aligned}$$
(43)
$$\begin{aligned}&({\textbf {f}},{\textbf {q}})\in SOL(\Omega ,{\textbf {F(n)}},{\textbf {G(n)}}) \end{aligned}$$
(44)

The objective (39) is to minimize the weighted sum of the network delay and emissions. Constraint (40) means that the total number of RSUs deployed on the network is no more than N due to limited budget. Constraint (41) is the RSU requirement for each link. It requires that the number of RSUs deployed on link \(a\in A\) is no less than \(\underline{n}_a\) and no more than \(\bar{n}_a\), where \(\underline{n}_a\) and \(\bar{n}_a\) are predetermined parameters whose values are related to the link length, the coverage of each RSU and the desired system performance in terms of communication reliability and robustness, etc. Constraint (42) is the definitional expression of link flow \(x_a\). Constraint (43) requires \(n_a\) to be integers. Constraint (44) is the equilibrium constraint which ensures the objective is minimized under equilibrium.

3 Solution algorithm

The (RSUD) model mentioned above is an integer program with equilibrium constraints which is difficult to solve due to the non-convex feasible region and the violation of Magasarian-Fromovitz constraint qualification (MFCQ). In order to obtain a promising solution to the (RSUD), we apply the active-set algorithm proposed by Zhang et al. (2009). It solves the problem by iteratively solving a series of simple subproblems and eventually reaching a strongly stationary point.

First, we introduce the gap function-based method (Aghassi et al. 2006) to solve the VI traffic assignment problem, which will constitute a subproblem incorporated in the active-set algorithm. The gap function-based method transforms a VI problem with polyhedral constraints into an equivalent nonlinear mathematical program and has been successfully used to solve many similar problems in literature (He et al. 2013; Chen et al. 2016, 2016). Specifically, the solution to VI problem (18) can be obtained by solving the following mathematical program (MP-1).

$$\begin{aligned}&\text {(MP-1)}\ \min _{{\textbf {f}},{\textbf {q}},\varvec{\eta },\varvec{\zeta }}\ \sum _{i\in I}\sum _{w\in W}\sum _{k\in K^w} F^{w,k}_i({\textbf {f}},{\textbf {q}})f^{wk}_i \\&\quad + \sum _{i\in i}\sum _{w\in W}G^w_i({\textbf {f}},{\textbf {q}})q^w_i - \sum _{w\in W} Q^w\xi ^w \end{aligned}$$
(45)
$$\begin{aligned} s.t.,\ (3),(9),(10),(21)-(24),(42), \text{and} \end{aligned}$$
$$\begin{aligned}&\theta ^w_iT^k + \ln {f^{wk}_i}\ge \eta ^w_i, \forall k\in K^w w\in W, i\in I \end{aligned}$$
(46)
$$\begin{aligned}&\theta C^w_i + \ln {\sum _{k\in K^w}\exp (-\theta ^w_iT^k)}\ge \xi ^w-\eta ^w_i, \\&\quad \forall w\in W, i\in I \end{aligned}$$
(47)

The objective function (45) is the gap between the primal and dual value of linear program (LP) associated with VI problem (18). Constraints (46) and (47) ensure the dual feasibility of the LP. Note that constraint (46) can be recast as \(f^{wk}_i\ge \exp (\eta ^w_i-\theta ^{wk}_iT^k)\), which renders any point with \(f^{wk}_i=0\) infeasible. (MP-1) is a continuous nonlinear program which in our study is solved using the nonlinear optimization solver CONOPT.Footnote 1

The second subproblem is defined as a nonlinear mathematical program (MP-2).

$$\begin{aligned} \text {(MP-2)}\ \min _{{\textbf {y,f,q}},\varvec{\mu ,\lambda }}\ \gamma _1\sum _{a\in A} t_a(x_a)x_a + \gamma _2\sum _{a\in A} e_a(x_a)x_a \end{aligned}$$
(48)
$$\begin{aligned} s.t.,\ (3),(9),(10),(21)-(24),(42), \text{and} \end{aligned}$$
$$\begin{aligned}&\theta ^w_iT^k + \ln {f^{wk}_i} - \mu ^w_i = 0, \forall k\in K^w, w\in W, i\in I \end{aligned}$$
(49)
$$\begin{aligned}&\theta C^w_i + \ln {q^w_i} - \lambda ^w_i = 0, \forall w\in W, i\in I \end{aligned}$$
(50)
$$\begin{aligned}&n_a = \sum _{m=1}^{M_a} 2^{m-1}y_{am}, \forall a\in A \end{aligned}$$
(51)
$$\begin{aligned}&y_{am} = 0, \forall (a,m)\in \Pi _0 \end{aligned}$$
(52)
$$\begin{aligned}&y_{am} = 1, \forall (a,m)\in \Pi _1 \end{aligned}$$
(53)

Constraints (49) and (50) are the equilibrium conditions (or the KKT conditions of VI problem (18)). (MP-2) shares the same objective with (RSUD) to minimize the delay and emissions under equilibrium constraints. However, every decision variable \(n_a\) in (MP-2) is fixed by \(M_a\) binary variable \(y_{am}\) via constraints (51)–(53), where \(M_a\) is the minimum number of binary variables required to represent \(n_a\) up to the level of \(\bar{n}_a\). The two index sets \(\Pi _0\) and \(\Pi _1\) are introduced to indicate whether \(y_{am}\) is set as 0 (if \((a,m)\in \Pi _0\)) or set as 1 (if \((a,m)\in \Pi _1\)). Note that since all binary variables \(y_{am}\) involved in (MP-2) are fixed using equality constraints (52) and (53). (MP-2) is treated as a continuous optimization problem. The goal of solving (MP-2) is to obtain the multipliers associated with constraints (52) and (53), which will provide guidance for us to adjust the two index sets. Solution obtained for (MP-1) will serve as an initial feasible solution to (MP-2) to facilitate the solution process. In (MP-2), the 0-1 variables \(y_{am}\)’s are fixed as either 1 or 0 by constraints (52) and (53). Hence, it can be regarded as a continuous nonlinear program. When (MP-2) is solved via CONOPT, the multipliers associated with constraints (52) and (53) will also be derived.

After we obtain the multipliers \(\alpha _{am}\) and \(\beta _{am}\) associated with constraints (52) and (53), respectively, the third subproblem (KP) plays its role to generate a potential adjustment to the deployment plan, i.e., the two index sets.

$$\begin{aligned}&\text {(KP)}\ \min _{{\textbf {u,v}}}\ \sum _{(a,m)\in \Pi _0} \alpha _{am}u_{am} - \sum _{(a,m)\in \Pi _1}\beta _{am}v_{am} \end{aligned}$$
(54)
$$\begin{aligned}&s.t.\ \sum _{(a,m)\in \Pi _0}2^{m-1}u_{am} - \sum _{(a,m)\in \Pi _1}2^{m-1}v_{am}\le N \\&\quad - \sum _{(a,m)\in \Pi _1}2^{m-1} \end{aligned}$$
(55)
$$\begin{aligned}&\underline{n}_a \le \sum _{m:(a,m)\in \Pi _1}2^{m-1} + \sum _{m:(a,m)\in \Pi _0}2^{m-1}u_{am} \\&\quad - \sum _{m:(a,m)\in \Pi _1}2^{m-1}v_{am}\le \bar{n}_a, \forall a\in A \end{aligned}$$
(56)
$$\begin{aligned}&\sum _{(a,m)\in \Pi _0} \alpha _{am}u_{am} - \sum _{(a,m)\in \Pi _1}\beta _{am}v_{am}\ge \kappa \end{aligned}$$
(57)
$$\begin{aligned}&u_{am}\in \{0,1\}, \forall (a,m)\in \Pi _0 \end{aligned}$$
(58)
$$\begin{aligned}&v_{am}\in \{0,1\}, \forall (a,m)\in \Pi _1 \end{aligned}$$
(59)

where \(u_{am}\) and \(v_{am}\) are binary decision variables to specify whether (a, m) should be shifted from set \(\Pi _0\) to \(\Pi _1\), and (a, m) shifted from set \(\Pi _1\) to \(\Pi _0\), respectively.

The objective function of (KP) measures the potential reduction resulted from the adjustment \(({\textbf {u,v}})\). Constraints (55) and (56) ensure that the adjustment will not violate the budget and link requirement constraints. (57) is used to rule out adjustments that fail to actually reduce the objective of (MP-2). Constraints (58) and (59) indicate the binary nature of the decision variables.

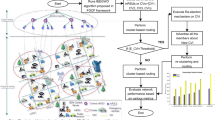
The overall procedure of the active-set algorithm applied to solve (RSUD) is described as follows. The flow chart of the algorithm is provided in Fig. 1.

  1. (1)

    Step 0: Set \(\zeta\) = 1, \(\Pi _0^1=\{(a,m): a\in A, m=1,2,\ldots ,M_a\}\), and \(\Pi _1^1=\emptyset\)

  2. (2)

    Step 1: Solve (MP-1) with RSU deployment plan \({\textbf {n}}^\zeta\) determined by \({\textbf {y}}^\zeta\) compatible with \((\Pi _0^\zeta ,\Pi _1^\zeta )\). Then use the solution to (MP-1) as the initial feasible solution for solving (MP-2) with \((\Pi _0^\zeta ,\Pi _0^\zeta )\), and obtain objective value \(Z^\zeta\), the solution \(({\textbf {y}}^\zeta ,{\textbf {f}}^\zeta ,{\textbf {q}}^\zeta , \varvec{\mu }^\zeta , \varvec{\lambda }^\zeta )\) and the multipliers \(\alpha ^\zeta _{am}\) and \(\beta ^\zeta _{am}\) associated with constraints (52) and (53), respectively.

  3. (3)

    Step 2: Set \(\kappa =-\infty\), and adjust the active sets \((\Pi _0^\zeta ,\Pi _1^\zeta )\) as follows:

    1. (a)

      Solve (KP) with multiplies \(\alpha ^\zeta _{am}\) and \(\beta ^\zeta _{am}\), and obtain the solution \((\hat{{\textbf {u}}},\hat{{\textbf {v}}})\). If the objective value is 0, stop and \(({\textbf {y}}^\zeta ,{\textbf {f}}^\zeta ,{\textbf {q}}^\zeta , \varvec{\mu }^\zeta , \varvec{\lambda }^\zeta )\) is the best solution. Otherwise, go to Step 2b.

    2. (b)

      Set

      1. i.

        \(\chi\) = \(\sum _{(a,m)\in \Pi _0} \alpha ^\zeta _{am}\hat{u}_{am} - \sum _{(a,m)\in \Pi _1}\beta ^\zeta _{am}\hat{v}_{am}\)

      2. ii.

        \(\hat{\Pi }_0 = \left( \Pi _0^\zeta -\left\{ (a,m)\in \Pi _0^\zeta :\hat{u}_{am}=1\right\} \right) \cup \left\{ (a,m)\in \Pi _1^\zeta :\hat{v}_{am}=1\right\}\)

      3. iii.

        \(\hat{\Pi }_1 = \left( \Pi _1^\zeta -\left\{ (a,m)\in \Pi _1^\zeta :\hat{v}_{am}=1\right\} \right) \cup \left\{ (a,m)\in \Pi _0^\zeta :\hat{u}_{am}=1\right\}\)

    3. (c)

      Solve (MP-1) with a deployment plan \({\textbf {y}}^\zeta\) compatible with \((\hat{\Pi }_0^\zeta ,\hat{\Pi }_1^\zeta )\). If the objective value \(Z'\) is less than \(Z^\zeta\), go to Step 2d because the pair \((\hat{\Pi }_0^\zeta ,\hat{\Pi }_1^\zeta )\) leads to a reduction in the objective. Otherwise, set \(\kappa = \chi + \varepsilon\), where \(\varepsilon >0\) is sufficiently small, and return to Step 2a.

    4. (d)

      Set \(\Pi _0^{\zeta +1}=\hat{\Pi }_0^\zeta ,\Pi _1^{\zeta +1}=\hat{\Pi }_1^\zeta\) and \(\zeta = \zeta +1\). Go to Step 1.

Fig. 1
figure 1

Flow chart of the solution algorithm

Full size image

It has been proved that the active-set algorithm terminates after a finite number of iterations and that the solution obtained by the algorithm must be a strongly stationary point. Interested readers are recommended to refer to Zhang et al. (2009) for more details.

4 Numerical examples

In this section, we will conduct numerical experiments to validate the performance of our proposed model and algorithm. The numerical experiments are based on the standard Nguyen-Dupuis network (see Fig. 2). There are four OD pairs whose demand is given in Table 2. The paths connecting the four OD pairs are listed in Table 7 in the Appendix.

Fig. 2
figure 2

Nguyen-Dupuis network (Nguyen and Dupuis 1984)

Full size image
Table 2 Travel demand of each OD pair
Full size table

We use the Bureau of Public Roads (BPR) function to measure the flow-dependent travel time on each link, i.e., the link travel time is

$$\begin{aligned} t_a(x_a) = t^0_a\left( 1+0.15\left( \frac{x_a}{B_a}\right) ^4\right) , \forall a\in A \end{aligned}$$
(60)

where \(t^0_a\) represents the free-flow travel time on link a and \(B_a\) is the capacity of the link. Their values are presented in Table 8 in the Appendix.

In Xie and Liu (2022), the dispersion parameter \(\theta _{\text{CAV}}^w\) for CAV users is assumed as a linear function in the penetration rate of CAV. Here, we adopt the same assumption, defining \(\theta ^w_{\text{CAV}} = g_{\theta }(\varvec{\rho }^w, q^w_{\text{CAV}})\) as a linear function in both the CAV penetration (\(\frac{q^w_{\text{CAV}}}{Q^w}\)) and the average RSU density of paths in \(K^w\) (\(\frac{1}{|K^w|}\sum _{k\in K^w}\rho ^k\)). Specifically,

$$\begin{aligned} \theta ^w_{\text{CAV}} = \theta ^w_{\text{RV}}+\psi _1 \frac{q^w_{\text{CAV}}}{Q^w} + \frac{\psi _2}{|K^w|}\sum _{k\in K^w}\rho ^k , \forall w\in W \end{aligned}$$
(61)

where \(\psi _1\) and \(\psi _2\) are coefficients that gauge the contribution of CAV penetration and RSU density to the information quality. The first term is the dispersion parameter for RV drivers to capture the information quality received by RV drivers. Equation (61) implies that the information quality of CAVs is higher than that of RVs due to the CAV technology and the assistance from RSUs.

For the function of long-term expected cost \(C^w_i\), we use the same formulation in Xie and Liu (2022), i.e.,

$$\begin{aligned} C^w_i = b^1_i \overline{T}^w_i + \frac{b^2_i\tau _i}{L_i}d^w + b^3_id^w, \forall w\in W, i\in I \end{aligned}$$
(62)

where \(b_i^1\) is the value of time when driving i-type vehicle, so the first term is the average travel time cost per trip. \(\tau _i\) is the vehicle purchase price and \(b^2_i\) is a scaling factor applied to the purchase price to capture other overhead costs (e.g., the purchase tax and the fee for granting a license plate, etc.). \(L_i\) is the maximum mileage that the vehicle can run in its life cycle. \(d^w\) is the average length of the paths in \(K^w\). The second term is the fixed cost of owning a vehicle averaged to a single trip. With \(b^3_i\) denoting the operational cost (e.g., the refuel cost and maintenance cost, etc.) per unit distance, the third term represents the operational cost per trip. The setting of these parameters are summarized in Table 9 in the Appendix. They are basically set in line with the settings in Xie and Liu (2022), with some of them scaled due to unit conversion.

The link requirement parameters \(\underline{n}_a\) and \(\bar{n}_a\) are set according to the settings in Li et al. (2020), in which the coverage of a RSU varies from 0.25 km to 1 km. Accordingly, the maximum RSU density is 4 RSUs per kilometer and we do not impose a lower bound on the number of RSUs to be deployment on each link, i.e., \(\underline{n}_a=0\). The specific value for \(\underline{n}_a\) and \(\bar{n}_a\) for each link is shown in Table 8 in the Appendix. Using this setting, the maximum number of RSU required for the network is 383. We thus set the RSU deployment budget N as 200 to make sure that the numerical example can reflect the impact of limited budget. Finally, we attribute equal weights to the two objectives, i.e., \(\gamma _1 = \gamma _2=1\).

Table 3 Validation of the path choice equilibrium
Full size table
Table 4 Validation of the vehicle type choice equilibrium
Full size table

To verify the correctness of our solution algorithm, we validate whether the flow and vehicle type choice pattern obtained from the algorithm is at equilibrium. The validation is accomplished through checking whether the solution satisfies the equilibrium conditions proposed in Proposition 1 and 2. The results are presented in Tables 3 and 4. As we can see from Table 3, for each OD pair w and vehicle type i, the expression \(\theta ^w_iT^k+\ln {f^wk_i}\) has the same value for all path \(k\in K^w\), and it equals \(\mu ^w_i=\ln {q^w_i}-\ln {\sum _{r\in K^w}\exp (-\theta ^w_iT^r)}\), which means that flow pattern is at equilibrium according to Proposition 1. Likewise, from Table 4 we can see that for each OD pair w, \(\theta C^w_i + \ln {q^w_i}\) has the same value for both vehicle types, which equals \(\lambda ^w = \ln {Q^w}-\ln {\sum _{j\in I}\exp (-\theta C^w_j)}\). Therefore, we can claim that the vehicle type choice is at equilibrium by Proposition 2.

Fig. 3
figure 3

Convergence of the solution algorithm

Full size image

Figure 3 shows the convergence behavior of the active-set algorithm. In our example, the algorithm terminates after a handful of iterations, which agrees with the theoretical property of the algorithm (Zhang et al. 2009). Moreover, it returns a considerably better solution than the initial solution, which must be a strongly stationary point of the origin problem (Zhang et al. 2009).

Table 5 Link performance before and after RSU deployment
Full size table

In Table 5, we present the vehicle flow, travel time and hourly emissions on each link before and after the optimal RSU deployment plan. It is assumed that there is no RSU installed on the network before the deployment. We can see that the optimal deployment plan has yield a significantly different pattern on the link flow, link travel time and link emissions. Specifically, such a different pattern has resulted in a considerable reduction on the total network delay (8.20%) and the emissions (7.13%), as shown in Table 5. It indicates that it is viable to effectively leverage the flow through RSU deployment to reduce both total system delay and emissions. Compared to the total delay and emissions, the increase in CAV penetration due to RSU deployment is not significant (0.54%), implying that the reduction of the former mainly roots in the change of path choices of CAV users but not the CAV adoption rate.

Table 6 Path flow and travel time before and after the deployment
Full size table

Table 6 presents the path flow and travel time before and after the optimal deployment of RSUs. The shortest path between each OD pair is in boldface. As we can see, the four shortest paths carry significantly more flow after the deployment, and three of them have a higher travel time than before. Moreover, all non-shortest paths become less congested after the deployment. This suggests that the RSU deployment can reduce travel time differences among paths between the same OD pair. It is interesting to note that though the travel time among different paths become more even, the flow distribution of RVs and CAVs exhibits different changes. For each OD pair, the RV flow is distributed more evenly on the paths after the deployment while the CAV flow tends to more concentrated. This is because RSUs provide more accurate information for CAV users, so they are more likely to select the shortest path despite of the reduced travel time difference among paths. Therefore, the shortest path for each OD pair attracts more CAVs after the deployment of RSUs. On the other hand, since RV drivers can hardly benefit from the RSU deployment in terms of information quality, their path choice will become more random as the travel time for different paths gets closer to each other.

Fig. 4
figure 4

Network delay and emissions under different deployment budgets

Full size image

Finally, we conduct a sensitivity analysis to figure out the resulted network delay and emissions under different budgets. The result is shown in Fig. 4. As expected, when we allow more RSUs to be deployed on the network, the network delay and emissions can be further reduced. However, the benefit from increasing deployment budget tends to diminish with the increase of budget. Therefore, before implementing any RSU deployment project aiming at reducing congestion and emissions, it is necessary for the practitioners to conduct careful cost-benefit analysis in order to well balance the investment and return, thereby attaining a desirable return-to-investment ratio.

5 Conclusions

Motivated by the fact that the deployment of RSUs may improve the quality of information received by CAVs, thereby influencing CAVs’ routing behaviors and adoption rate, we investigate the optimal deployment plan of RSUs under the mixed traffic flow to reduce network congestion and emissions. First, we develop an SUE model to describe the equilibrium path flow and vehicle type choice pattern given a fixed RSU deployment plan. With the established equilibrium model, the deployment of RSUs is modeled as a mathematical program with equilibrium constraints. The active-set algorithm is adopted to solve the deployment model efficiently, in which the equilibrium conditions are reformulated as a VI problem and solved with gap function-based method. Numerical experiments are conducted to demonstrate the viability of deploying RSUs to achieve a desirable flow pattern with less congestion and emissions. It is also shown that RSU deployment have different impacts on RV and CAV flows. The sensitivity analysis suggests that the marginal benefit from RSU deployment may decrease with the budget for RSU deployment.

There are a few possible extensions to this work. For example, models can be extended to integrate other management strategies such as congestion/emission pricing and tradable credit to further regulate CAV and RV users’ routing behaviors. Moreover, since RSUs can provide information in a real-time manner, CAV users may make their route choice dynamically. Therefore, future research may extend the deployment model of RSUs by considering the dynamic traffic assignment in the lower level problem.