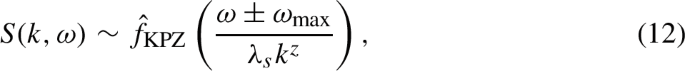Abstract
Energy transfer in small nano-sized systems can be very different from that in their macroscopic counterparts due to reduced dimensionality, interaction with surfaces, disorder, and large fluctuations. Those ingredients may induce non-diffusive heat transfer that requires to be taken into account on small scales. We provide an overview of the recent advances in this field from the points of view of nonequilibrium statistical mechanics and atomistic simulations. We summarize the underlying basic properties leading to violations of the standard diffusive picture of heat transport and its universal features, with some historical perspective. We complete this scenario by illustrating also the effects of long-range interaction and integrability on non-diffusive transport. Then we discuss how all of these features can be exploited for thermal management, rectification and to improve the efficiency of energy conversion. We conclude with a review on recent achievements in atomistic simulations of anomalous heat transport in single polymers, nanotubes and two-dimensional materials. A short account of the existing experimental literature is also given.
Similar content being viewed by others
1 Introduction
Energy transfer in nonlinear systems occurs in many physical contexts, ranging from condensed matter to optics. Besides its basic interest, understanding the principles of vibrational energy transport at the nanoscale is of importance to eventually improve our capability to manage thermal transport on small-scale devices [1]. In the case of phononic systems, where heat is mostly transported by lattice vibrations, this calls for a deeper understanding of the properties of strongly anharmonic and/or disordered crystals and artificial materials. Nonlinear effects are essential in many respects: in the first place, they determine thermal transport properties. When reducing the system size towards the micro and nano-scale, a series of novel effects appear. Temperature gradients can become very large, leading to non-linear response. Also, the role of thermal contact and interfaces may not be negligible, and in general heat-current fluctuations may be relevant, and one has to treat them within a suitable thermodynamic approach for small systems. Particularly dramatic effects occur in reduced dimensions, where nonlinear interactions of energy fluctuations lead to anomalous conductivity.
In this article, we will review the main features of non-Fourier (superdiffusive) heat conduction in low-dimensional many-body systems. Starting from simple theoretical models (anharmonic chains) we will argue that this phenomenon displays remarkable universal properties. As it is known, the idea of universality is very relevant in statistical physics. It tells us that some quantitative relations hold, independently of the microscopic details. The concept was born out of the theory of critical phenomena: for instance, any ferromagnetic transition exhibits the same dependence of the magnetization on temperature if the underlying Hamiltonian has the same symmetry.
In the context of nonequilibrium processes (like heat transport), this is even more striking. For instance, if we have a nearly one-dimensional system with some symmetries leading to momentum, energy, and density conservation, we expect superdiffusive transport with given exponents, independently of the actual microscopic forces. As a concrete example, the simple Fermi–Pasta–Ulam–Tsingou (FPUT) model discussed below is expected to be in the same universality class of transport as, say, a single-walled nanotube or a nanowire, made of complicated assemblies of atoms.
Building on this theoretical background, we describe how these features can be exploited to achieve control and enhancement of thermal energy conversion. The simplest case is the one in which nonlinear interaction can be exploited to obtain a thermal rectifier. Anomalous conduction can be also employed to enhance the conversion of thermal energy into mechanical work, as it occurs in thermoelectricity and thermodiffusion.
A crucial issue is the applicability of the theoretical concepts to real nanomaterials. The fabrication of one- and two-dimensional nanomaterials (nanotubes, nanowires, graphene, two-dimensional semiconductor membranes, etc.) is nowadays a concrete experimental possibility. For the sake of illustration, a typical setup we have in mind is sketched in Fig. 1. Thus, one may hope to test experimentally the predictions from statistical physics. In this respect, molecular dynamics (MD) is a fundamental tool to investigate and test theories. We will provide a review of current research focused on non-Fourier heat transport.
This work complements existing reviews of the research done in the nonequilibrium statistical physics community [2,3,4,5] by reporting some recent advances, but also with an eye to applying the concepts to thermal management and to realistic atomic simulations, of interest for condensed-matter. Although our main focus is on the microscopic foundations, in this respect, we have to mention that thermodynamic and mesoscopic phenomenological approaches have also been worked out to tackle the problem of non-Fourier heat transport in various materials and devices. This leads to various generalization of the heat conduction laws. For the sake of space, we cannot fully account for all these contributions in this review: the reader can recover a basic information about these approaches in the existing literature [6,7,8,9,10,11]. For completeness, we mention that reviews in non-Fourier heat transport from a phonon physics viewpoint can be found in [12] and [13]. It is now recognized that the reduced dimensionality originates unusual size-dependent features in nanomaterials. Phonon confinement, surface, and interfacial scatterings at the nano-scale are also relevant research topics in this context [13]. Before entering the main matter, we give a brief historical account.
Sketch of a nanoscale heat transfer experimental setup to measure the heat conductance of a thin nanosized object in thermal contact with two leads, acting as thermal reservoirs at different temperatures \(T_\textrm{H}>T_\textrm{C}\). Lower figure: a simple idealized model, for vibrational energy transport in a one-dimensional structure. It consist of an anharmonic chain in contacts with two heat reservoirs at different temperatures. The reservoirs can be modeled, for instance, by adding Langevin thermostats at assigned temperatures [2, 14]
1.1 Historical perspective
From a historical perspective, one discovers that the problem of non-diffusive heat transport affected quite soon the theoretical foundations of statistical mechanics. At the end of the nineteenth century, Boltzmann’s equation had solved both the equilibrium problem and the hydrodynamics of the ideal gas [15] within a fully consistent approach, which allowed to interpret phenomenological equations, such as the Navier–Stokes and the Heat equation, as direct outcomes of the kinetic theory. The interest for studying the problem of energy (heat) transport in microscopic models of matter, rather than simply relying upon the coarse-grained description of an ideal fluid, emerged quite soon in the twentieth century. For instance, P. Debye in the 1930 s argued that the problem of heat transport in solids could not be modeled by a harmonic crystal. In fact, the thermodynamics of such a system amounts to a gas of non-interacting quasi-particles, in which the harmonic waves (that now we usually call phonons), propagate ballistically at the speed of sound. Accordingly, no diffusion mechanism can be at work in such a model of a solid that propagates any perturbation ballistically, as a heat superconductor. The Dutch physicist suggested that nonlinear interactions and/or disorder should be included in the model, in order to allow for a microscopic mechanism of phonons scattering. His pupil, R. Peierls, approached this problem in the framework of quantum mechanics with phonons being the basic ingredients as quantized linear waves. Taking advantage of the arguments raised by Debye, he built up a phenomenological quantum theory of heat transport in solids by introducing the so-called umklapp processes, i.e. effective interactions among phonons, treated as a perturbative first-order correction of the unrealistic harmonic limit (more precisely, they correspond to phonon scattering processes that do not conserve the quasi-momentum, see [16]). This “trick” was able to restore diffusion as the basic mechanism yielding energy transport, as expected also in classical models.
The seminal considerations raised by Debye certainly inspired also E. Fermi to pursue the other possibility, i.e. including explicitly the role of nonlinearity in classical models. Fermi could tackle this problem because in the last part of his life he and his collaborators (J. Pasta, S. Ulam and M. Tsingou) had access to the biggest computer facility of the time, the MANIAC digital computer in Los Alamos, designed by J. von Neumann. They used MANIAC to perform the first numerical simulation of the dynamics of a 1D anharmonic crystal. Fermi expected that the presence of nonlinear interactions could allow any out-of-equilibrium initial condition to relax spontaneously to thermodynamic equilibrium, signaled by energy equipartition among the normal (Fourier) modes (a more appropriate denomination of phonons in a classical system). Contrary to his expectations, they found that the energy of the out-of-equilibrium initial condition (typically a single Fourier mode) initially spreads its energy to other normal modes, but later on, exhibits a quasi-periodic recurrence to the initial state. Nowadays we know that this peculiar phenomenon is due to the presence of soliton-like waves (described by the Korteweg–deVries partial differential equation) in the low-energy limit of the model, which corresponds to the range of parameters explored by Fermi and coworkers. Fermi was really puzzled by having not met what he had reasonably conjectured and the account of these numerical simulations appeared only in 1954, the same year when Fermi passed away, just as an internal Los Alamos report [17]. It is worth pointing out that the quasi-periodic recurrence of the initial states not only challenged the spontaneous evolution to thermodynamic equilibrium, but it was also incompatible with the presence of any diffusive mechanism for energy transport in the FPUT model. To make a long story short, we can just mention that energy equipartition was eventually observed in numerical experiments (performed by computers definitely much more powerful than MANIAC), exploring the FPUT model for sufficiently large values of the energy and for a long enough time [18].
Still following a historical pathway, we have to mention that a complete mathematical description of the peculiar features of a harmonic chain, conjectured by P. Debye, was provided in a seminal paper by Rieder, Lebowitz and Lieb [19], who obtained an explicit solution of the model of a chain of harmonically coupled oscillators (with fixed boundary conditions) in contact at its boundaries with stochastic Langevin heat baths at different temperatures \(T_+\) and \(T_-\). A clear signature of ballistic energy transport is testified by an essentially flat temperature profile in the bulk of the chain at \(T= (T_+ +T_-)/2\), which decays abruptly at the bath temperatures very close to the corresponding boundaries. Moreover, the heat flux is found to be proportional to the temperature difference, rather than to the temperature gradient.
This paper provided inspiration to other applied mathematicians for exploring the other suggestion by P. Debye, i.e. including disorder as an ingredient of the model. The simplest way amounts to introducing isotopic disorder in the harmonic chain by assigning random masses (selected by some probability distribution function) to each harmonic oscillator. Relying upon a naive extrapolation of localization theory, one could guess that isotopic disorder should turn the homogeneous superconductor into a perfect insulator, because any propagating energy perturbation should eventually localize, due to the presence of one-dimensional disorder. This guess is not entirely correct, because it was found that the mechanism of heat transport in an isotopically disordered chain crucially depends on the adopted boundary conditions. One should always take into account that, at variance with equilibrium properties, out-of-equilibrium ones typically exhibit a strong dependence on the boundary conditions. A preliminary important achievement was the rigorous proof that the harmonic chain with isotopic disorder evolves to a unique stationary non-equilibrium state [20, 21]. Summarizing a long story (for details see [2]), it was also proved that for fixed boundary conditions the heat conductivity \(\kappa \) of the disordered harmonic chain of size N vanishes in the thermodynamic limit as
while for free boundary conditions it diverges in the thermodynamic limit as
Accordingly, the latter case shows that anomalous conductivity already emerges in a disordered harmonic chain with free boundary conditions, thus indicating that despite the presence of isotopic disorder, superdiffusive heat transport already emerges in such conditions.
Almost in the same period of time when these contributions about disordered harmonic chains appeared, another community of researchers, concerned with the study of hydrodynamic models, pointed out that anomalous hydrodynamic behavior is a distinctive feature of real fluids [22, 23], through the manifestation of peculiar memory kernels characterizing their space-time correlation functions, and, accordingly, the associated transport coefficients through the Green–Kubo formula (see [24]). Conversely, the attempt of providing a general theoretical approach to the problem of heat transport in fluid dynamics (see [25]) pointed out that superdiffusive (i.e., anomalous) transport properties should characterize one- and two-dimensional fluids—an outcome that, at the time, appeared almost as a mathematical curiosity, in the absence of experimental tests to be performed on real physical systems. Nowadays, we are facing the possibility of exploring predictions originated by suitable mathematical models in the realm of nanophysics, where such effects are sizable and of primary interest for material science, as widely reported in this review article.
The last ingredient invoked for reconciling normal transport properties with low-dimensional systems was deterministic chaos. The basic conjecture was that models of many-body systems exhibiting chaotic dynamics should generate spontaneously diffusive-like behavior of energy perturbations, regardless of their dimensionality, and any other peculiar feature of the model at hand. In fact, the first numerical study of the 1D chaotic model known as Ding-a-lingFootnote 1 confirmed the above conjecture [26]. Nowadays, we know that normal transport properties in this chaotic model are just a mere consequence of the presence of the on-site force acting on each particle, which prevents the possibility of total momentum conservation, because translation invariance is broken by the local harmonic forces. In fact, contrary to what was conjectured about chaotic systems, when the total length, the total momentum and the total energy of any 1D and 2D chaotic system are conserved, anomalous transport sets in. This is what we are going to discuss broadly in Sect. 2.
1.2 Outline of the paper
In this work, we will provide an updated review of the research on the problem of anomalous transport, with an eye to its effect on nanoscale systems. The choice of topics reflects of course our own work and expertise, and we refer the reader to the Bibliography for a more complete overview.
In Sect. 2 we briefly introduce the main features as studied for simple models, namely low-dimensional lattices of coupled nonlinear oscillators. We recap the relevant phenomena and numerical evidence of anomalous energy transport and emphasize their universal features. Some recent results, including the effects of magnetic fields, long-range forces, and weak chaos will be reviewed. To demonstrate the generality of these results, we also report on some simulation studies of low-dimensional fluids.
Section 3 addresses the general problem of how to control and manage heat transfer in nanosized structures, exploiting the general knowledge gained by recent research. The section deals first with thermal rectification and possible enhancement mechanisms of heat-to-work energy conversion. Then we review the counterintuitive phenomenon of inverse coupled currents, whereby currents flow against both temperature and concentration gradients.
As a step towards implementation of the above concepts in realistic low-dimensional structures, in Sect. 4, we review the current state of the art of molecular dynamics simulations of nanosystems, that are the best candidates to observe and exploit anomalous heat conduction in devices. We first recall the basic simulation methods, which can be grouped into equilibrium and non-equilibrium molecular dynamics approaches. We then describe anomalous transport in three cases: isolated single polymers, individual carbon nanotubes, and graphene. These appear to be ideal candidates to test the theoretical predictions in one and two dimensions. Then we discuss the relevance of hydrodynamic effects on non-Fourier heat transport at the nanoscale. Finally, we review some of the works in which the original concept of thermal rectification based on phonons non-linearity has been investigated.
A few experimental works have been reported to try to validate the theoretical predictions. In Sect. 5, we briefly point to the relevant literature.
2 Statistical mechanics of non-Fourier heat transport
In this section, we review the main features of anomalous energy transport and violations of Fourier law in low-dimensional non-linear systems from the point of view of statistical physics. For a more extensive account, we refer the reader to existing review papers [2, 3, 5, 27].
Anomalous transport emerges as a hydrodynamic effect due to the conspiracy of reduced space-dimensionality, conservation laws, and non-linear interactions, yielding nonstandard relaxation properties even in a linear response regime. The most concise, heuristic way to describe what anomalous energy transport is about, is to imagine that the energy carriers (e.g. phonons in a low-dimensional structure) propagate superdiffusively, i.e. in a non-Brownian way. Indeed, most of the anomalous transport phenomenology in such many-body systems can be effectively described as a random propagation [28] of the energy carriers, as demonstrated extensively in the literature [29,30,31]. A Lévy walk is a stochastic process where a particle undergoes random jumps with constant speed and for random times distributed as an inverse power-law distribution [28]. This description entails that the mean free path becomes effectively infinite, thus leading to the breakdown of standard kinetic approaches.
2.1 Anomalous heat transport in classical anharmonic chains
As a reference system, we will consider the class of models, represented by a Hamiltonian of the following form:
The model admits two physical interpretations: one as a discretization of a scalar field q(x, t) on a one-dimensional lattice, \(q_n(t)\equiv q(n,t)\). Otherwise, one can regard \(q_n\) as physical positions on the line, i.e as a 1D fluid. One implicitly assumes that particle order is preserved. For isolated chains, one typically enforces periodic boundary conditions \(q_{N+1}=q_{1}+L\), where L is the total length. Hamiltonian (3) has the invariance property under translations \(q_n \rightarrow q_n + cst\) leading to momentum conservation. Moreover, the “stretch” variable \(\sum _n(q_{n+1}-q_n)\) is also conserved. Since we are interested in heat transport, one can set the total momentum to zero without loss of generality. The relevant state variables of microcanonical equilibrium are the specific energy (i.e., the energy per particle) \(h=H/N\) and the elongation \(l=L/N\) (i.e., the inverse of the particle density). If U is quadratic around the equilibrium state, the chain admits a single branch of acoustic phonons.
Common choices for the interaction potential are the famous FPUT potential
or the Lennard–Jones one [32]
Throughout this paper, we adopt suitable adimensional model units to simplify the notation.
The main results, emerging from a long series of contributions, can be summarized as follows— [2, 3, 5, 27]. Models of the form (3) having the three conservation laws described above, generically display anomalous transport and relaxation features. In other terms, Fourier’s law does not hold: the kinetics of energy carriers is so correlated that they are able to propagate faster than in the ordinary (diffusive) case.
Such a behaviour manifests itself in the simulations in various facets [33]:
-
The finite-size heat conductivity \(\kappa (L)\) diverges in the limit of a large system size \(L\rightarrow \infty \) as, \(\kappa (L) \;\propto \; L^\gamma \) [34], i.e. the heat transport coefficient is ill-defined in the thermodynamic limit.
-
The equilibrium correlation function of the total energy current J displays a nonintegrable long-time tail \(\langle J(t)J(0)\rangle \propto t^{-(1-\delta )}\), with \(0\le \delta < 1\) [35, 36]. Accordingly, the Green–Kubo formula yields an infinite value of the conductivity.Footnote 2
-
Energy perturbations propagate superdiffusively [29, 37]: a local disturbance of the energy field spreads, while its variance broadens in time as \(\sigma ^2\propto t^{\beta }\), with \(\beta > 1\).
-
Temperature profiles in the nonequilibrium steady states are intrinsically nonlinear, even for vanishing applied temperature gradients. Typically they are the solution of a fractional heat equation instead of the standard heat equation, [30, 38, 39].
There is a large body of numerical evidence that the above features occur generically in 1D, whenever the conservation of energy, momentum and length hold. As it is known, this is related to the existence of long-wavelength (Goldstone) modes (an acoustic phonon branch in the linear spectrum) that are very weakly damped. Moreover, the exponents that characterize the phenomena listed above are related, as they are different facets of the same physical effects. For instance, if there is a finite propagation speed one can argue that \(\delta =\gamma \), etc. [2, 3, 5, 27].
As for the dependence on the dimension, one can find evidence of anomalous transport and a diverging heat conductivity in 2D model, like for instance a 2D version of the the FPUT model. Typically, the finite-size conductivity data are consistent with a logarithmic dependence with the system size L [40,41,42]. Moreover, normal diffusive transport is restored in the 3D case [43, 44] (with the exception of integrable models like a purely harmonic crystal).
The importance of conservation laws can be appreciated by examining the following examples. Consider first the anharmonic chains where a local external pinning potential V is added to the Hamiltonian,
The main difference is that this class of models has only one global conserved quantity, namely energy. The dispersion in the linear limit is gapped, i.e. it admits only optical phonon modes. Relevant examples in this class that have been discussed in the present context are the discrete \(\phi ^4\) theory [45] and the Frenkel–Kontorova model [46]. Generally, the addition of pinning forces suffices to make the anomalies disappear and restore Fourier’s law and standard heat diffusion. Another interesting and well-studied example [47, 48] is the rotor (or Hamiltonian XY) chain, namely (3) with
Here, x has to be read as a difference between angles, and thus the stretch variable is no longer globally conserved by a change of relative phases by \(2\pi \). So the model has two conserved quantities only, and transport is normal with finite thermal conductivity and finite Onsager coefficients [49,50,51]. (A more sound theoretical justification for those observations will be reviewed below).
For completeness, we also mention another important model related to the ones mentioned above, namely the discrete nonlinear Schrödinger (DNLS) lattice (also termed the discrete Gross–Pitaevskii equation). As it is known, it has important applications in many domains, for instance, electronic transport in biomolecules and atomic condensates in optical lattices [52]. It is defined by the Hamiltonian
whose equation of motion can be written in terms of the complex variable \(z_n = (p_n + i q_n)/\sqrt{2}\) as
Besides the total energy, the system admits a second constant of motion, namely the total norm \(A = \sum _{n=1}^N \mid z_n \mid ^2 \), which, depending on the physical context, can be interpreted as the gas particle number, optical power, etc. At variance with its continuum counterpart, the DNLS is non-integrable and typically displays chaotic dynamics. There is evidence that transport is normal for DNLS, i.e. that the elements of the Onsager matrix are well-defined in the thermodynamic limit [53,54,55,56].
To end this section, let us mention that the actual simulations described here turned out to be quite challenging, despite the apparent simplicity of the models. As it is known, equilibrium simulations of correlation functions are affected by large statistical fluctuations. Reliable measurements of transport coefficients in nonequilibrium simulations can also be very difficult, while the presence of boundary resistances and strong finite-size effects are usually serious issues. It is worth mentioning that improved methods, which originated in the statistical physics community, seem very promising. For instance, importance sampling schemes aiming at sampling the probability of rare current fluctuation have been proposed [57]. This approach, based on the so-called cloning algorithms, seems quite effective in assessing the anomalous transport properties of low-dimensional nanomaterials [58].
2.2 Kardar–Parisi–Zhang universality
The main theoretical insight that has been achieved is the intimate relation between the anharmonic chain and one of the most important equations in nonequilibrium statistical physics, the celebrated Kardar–Parisi–Zhang (KPZ) equation, also known as the noisy (or fluctuating) Burgers equation. The latter was originally introduced in the (seemingly unrelated) context of surface growth [59], but turned out to be a paradigm of many non-equilibrium problems in physics. In the case of a scalar stochastic field h(x, t) in one spatial dimension it reads
where \(\eta (x,t)\) represents a Gaussian white noise with \(\langle \eta (x,t)\eta (x',t')\rangle \)=\(2D\delta (x-x')\delta (t-t')\) and \(\nu ,\kappa ,D\) are the relevant parameters.
The connection between the KPZ and anomalous transport has been derived within the nonlinear fluctuating hydrodynamics approach [60, 61]. The theory is able to justify and predict several universal features of anomalous transport in anharmonic chains. This implies that their large-scale dynamical properties are in the same dynamical universality class as Eq. (9). We give here a preliminary account, referring the reader to [60, 62] for details. The main entities are the random fields describing deviations of the conserved quantities with respect to their stationary values. The role of fluctuations is taken into account by the renormalization group or some kind of self-consistent theory.
More precisely, large-scale fluctuations result from three stochastic fields or modes: two sound modes, \(\phi _\pm \), traveling at speed c in opposite directions, and one stationary but decaying heat mode, \(\phi _0\). Loosely speaking, we can represent e.g. the displacement field as the superposition of counter-propagating plane waves, modulated by an envelope that is ruled at large scales by Eq. (9). The quantities of interest are the equilibrium spatiotemporal correlation functions \(C_{s s'}(x,t)=\langle \phi _s(x,t) \phi _{s'}(0,0)\rangle \), where \(s,s'=-,0,+\). Because the modes separate linearly in time, one argues that the corresponding equations decouple into three single-component equations. Those for the sound modes have precisely the structure of the noisy Burgers equation [60]. For the heat mode, the self-coupling coefficient vanishes, whatever the interaction potential. Sub-leading corrections must be considered within the mode-coupling approximation, resulting in the symmetric Lévy distribution.
For the generic case of non-zero pressure, which corresponds either to asymmetric inter-particle potentials or to an externally applied stress, the theory predicts the following scaling form for the auto-correlation functions of the modes
Remarkably, the scaling function \(f_{\textrm{KPZ}}\) is universal and known exactly (see [60] and references therein). Also, \(f_{\textrm{LW}}^\nu (x)\) denotes the Lévy function of index \(\nu \), defined as the Fourier transform of the characteristic function \(e^{-\mid k \mid ^\nu }\). Such a family of functions is well-known and (not by chance) appears in the theory of anomalous diffusion [63]. The non-universal features are in the \(\lambda _s\) and \(\lambda _e\), that are model-dependent parameters. Therefore, fluctuations of observables display, in the hydrodynamic limit, anomalous dynamical scaling, as manifested by the \(t^{1/z}\) dependence of correlation on time, as seen in Eq. (10). Here the dynamical exponent \(z=3/2\) is different from \(z=2\), expected for a standard diffusive process.Footnote 3 As a consequence of such scaling, it has been argued that the energy current correlations decay with an exponent \(\delta =1/3\) i.e. \(\kappa (L) \sim L^{1/3}\).
Even from such a short outline, it is evident that the hydrodynamic approach provides several predictions. Most of them have been successfully tested for several models [64,65,66], including anharmonic chains with three conserved quantities like the FPUT model [67, 68]. Also, the KPZ scaling is not limited to scalar displacements, but applies as well to quasi-1D chains with 3D motions [69]. It should be however recognized that departures from universality have been reported in simulations of specific hard-point gas models [70].
Another remarkable feature is that the KPZ scaling may hold approximately in some regimes. For instance, it accounts well for the low-temperature hydrodynamics of the DNLS equation (8) in the regime where there is an approximate third conservation law [55, 71]. It should however be kept in mind that the observability of KPZ scaling may be hindered by significant scale effects, especially when the dynamics is only weakly chaotic [72] (we will come back to this in Sect. 2.4 below).
Although the KPZ class is expected to be generic, there may be specific cases that belong to a different (non-KPZ) universality class by virtue of additional symmetries. This is the case of anharmonic chains models with symmetric interaction potentials like the FPUT-\(\beta \) model, namely the potential in Eq. (4) with \(\alpha =0\) [73, 74], as well as of chains with conservative noise (e.g., the noisy harmonic [75, 76] or nonlinear [77, 78] chains). Physically, this condition corresponds to the case where the chain is at zero pressure [74]. This possibility is also accounted for by the fluctuating hydrodynamics approach. Indeed, for an even potential, the mode-coupling approximation predicts a different scaling of the correlation functions [60]:
where \(f_\textrm{G}(x)\) is the unit Gaussian with zero mean. This class would correspond to a diverging finite-size conductivity with \(\gamma =1/2\). It is worth also mentioning, that the kinetic theory approach confirms a non-KPZ behavior for the FPUT-\(\beta \) model [79,80,81,82], albeit with a different exponent \(\gamma =2/5\), which is pretty close to the numerical one [73, 83].
To conclude, it has been also argued that the two main nonequilibrium universality classes, the diffusive and KPZ, are only two cases of an infinite discrete family. The members of this family can be identified by their dynamical exponent, which depends on both the number of conserved quantities and the coupling among their hydrodynamic modes [84].
2.3 Anomalous transport with broken time-reversal
The effect of time-symmetry breaking on anomalous transport has been considered in [85, 86] that investigated a one-dimensional chain of charged beads, interacting with a quadratic potential, in the presence of an external magnetic field \(\textbf{B}\). For \(\textbf{B}=0\), \(\delta = \frac{1}{2}\), thus indicating the presence of anomalous transport and a divergent heat conductivity \(\kappa (L) \sim L^{\frac{1}{2}}\). For nonvanishing \(\textbf{B}\) the total pseudo-momentum is conserved, and the hydrodynamics of the model must be modified. Actually, numerical and analytic estimates indicate that in this case, the exponent \(\delta \) may turn to a value different from \(\frac{1}{2}\). In particular, in [85] two different cases were considered: the one where oscillators have the same charge and the one where oscillators have alternate charges of sign \((-1)^n\), n being the integer index numbering oscillators along the chain. In the former case, the sound velocity vanishes, and the energy correlator exhibits a heat peak centered at the origin and spreading in time. Conversely, in the latter case, the sound velocity is finite and its value depends on \(\textbf{B}\). Here, the heat mode is coupled to sound modes propagating through the chain. The exponent \(\gamma \) is the same obtained for \(\textbf{B} = 0\), i.e. \(\gamma = \frac{1}{2}\).
In the case of equally charged beads, one finds a novel exponent \(\gamma =\frac{3}{8}\), which corresponds to a different universality class. An important remark on this new exponent is that, in the absence of a finite sound velocity, the identification of the exponents \(\delta \) and \(\gamma \), invoked above, no longer holds. Indeed, in this case, one has \(\delta \approx \frac{3}{4}\). Rigorous estimates of these exponents also for the \(d=2\) and \(d=3\) versions of the model have been obtained through the asymptotes of the corresponding Green–Kubo integrals, where the deterministic dynamics has been substituted with a stochastic version that conserves the same quantities [86].
2.4 Integrable models and their perturbations
The above results are mostly obtained in a strongly nonlinear regime or more generally far from any integrable limit. For the FPUT model, this means working at high enough energies/temperatures to avoid all the difficulties induced by quasi-integrability and the associated slow relaxation to equilibrium.
Integrable systems constitute per se a relevant case and experienced a renovated interest in recent years. In the framework of this review article, the reference example is certainly the celebrated Toda chain, namely the model in Eq. (3) with
As intuitively expected, heat transport is ballistic due to its integrability and the associated solitonic solution [87]. Mathematically, this is expressed by saying that there is a non-vanishing Drude weight, namely a zero-frequency component of the energy-current, and power spectrum [88, 89]. A lower bound of the Drude weight can be estimated by making use of Mazur inequality [90] in terms of correlations between the currents themselves and the conserved quantities. See [88, 89] for application to the Toda case. However, the idea of solitons transporting energy as independent particles is somehow too simplistic. At variance with the harmonic chain, which is also integrable, but whose proper modes are non-interacting phonons, the Toda chain should rather be considered as an interacting integrable system [91]. In simple terms, it means that the quasi-particles (the famous Toda solitons) experience a stochastic sequence of spatial shifts as they move through the lattice, interacting with other excitations without momentum exchange. This yields a kind of non-dissipative diffusion [92] that reflects in the calculation of the transport coefficients by the Green–Kubo formula, indicating the presence of a finite Onsager coefficient. The latter corresponds to a diffusive process on top of the dominant ballistic one [89, 93, 94].
In general, equilibrium correlations of integrable models should display a ballistic scaling, as indeed confirmed for the Toda chain [93]. There are some exceptions to this rule, like in the case of the scaling behavior of the integrable lattice Landau–Lifshitz spin chain that, for the case with zero mean magnetization, has a scaling function identical to the one obtained for the KPZ equation [95].
A natural question concerns the behavior when a generic perturbation is applied to an otherwise integrable system. The first observation is that the actual form of perturbation is relevant. For instance, adding a quadratic pinning potential \(V(x)=x^2/2 \) to the Toda chain does restore standard diffusive transport, but numerical simulations show that long-range correlations are preserved over relatively large scales [39, 94]. Moreover, weak perturbations that conserve momentum (and are thus expected to display anomalous transport in the KPZ class) display instead significant deviations [78] and even diffusive transport over the accessible simulation ranges [96].
The relevant issue regards the typical length scales over which the anomalous transport is restored by the effect of a perturbation. The length-independent flux exhibited by integrable systems is the result of the free displacement of quasi-particles (the integrals of motion, such as solitons) from the hot towards the cold reservoir. In the vicinity of the integrable limit, as a result of mutual interactions, the quasi-particles acquire a finite and large mean free path \(\ell \). A purely ballistic behavior is observed for \(L<\ell \). On the other hand, \(L>\ell \) is not a sufficient condition to observe a crossover toward the anomalous behavior predicted by the above-mentioned theoretical arguments. In fact, it is necessary for L to be so long that the normal flux induced by inter-particle scattering becomes negligible. Altogether, upon increasing L at fixed \(\ell \), one should observe a first ballistic regime followed by a kinetic (diffusive) one, until eventually, the asymptotic hydrodynamic (anomalous) regime is attained. The three different regimes are observable only provided the relevant length scales are widely separated.
Based on these heuristic considerations, one may look for a decomposition of heat flux \(J(L,\varepsilon )\) as [72]
where \(\varepsilon \) measures the perturbation strength i.e. the distance from the integrable limit, \(J_\textrm{A}\) is the anomalous hydrodynamic part, and \(J_\textrm{N}\) is the kinetic contribution, accounting for the energy transported by the weakly interacting quasi-particles. As explained above, for \(L\rightarrow \infty \), we expect \(J_\textrm{A} \approx L^{\gamma -1}\) with \(\gamma =1/3\) in systems belonging to the KPZ class.
Following a kinetic argument [97], we argue that \(J_\textrm{N}\) must be only a function of \(\xi =L/\ell \), which is the ratio expressed in units of the mean free path \(\ell \), the only relevant scale. Moreover, \(J_\textrm{N}\) should display a crossover from ballistic to diffusive regimes depending on \(\xi \), namely it should approach a constant for small \(\xi \) and be proportional to \(1/\xi \) for large \(\xi \). A simple interpolating formula would thus be
where r is a constant accounting for the boundary resistance [98] and \(j_0\) is an additional constant.
Approaching the integrable limit, the mean free path must diverge, and it is natural to assume that \(\ell \approx \varepsilon ^{-\theta }\), where \(\theta >0\) is a system-dependent exponent. As long as \(J_\textrm{A}(L,\varepsilon )\) does not display any singularity for \(\varepsilon \rightarrow 0\) (we return to this point below), we can neglect its dependence on \(\varepsilon \). Altogether, Eq. (15) can be approximated for large L as
where \(c_\textrm{A}\) and \(c_\textrm{N}\) are two suitable parameters. Accordingly, the anomalous contribution dominates only above the crossover length \(\ell _\textrm{c} \approx \varepsilon ^{-\theta /\gamma }\). For \(L\le \ell _\textrm{c}\), heat conduction is dominated by \(J_\textrm{N}\). In particular, within the range \([\ell =\varepsilon ^{-\theta },\ell _\textrm{c}]\) an apparent normal conductivity is expected, which is nothing but a finite size effect.
The above description accounts very well for the numerical data for the perturbed Toda and hard-point gas models [72].
The standard case of the perturbed harmonic chain deserves a special consideration from this point of view. Numerical analysis of the FPUT-\(\beta \) model at very low energy, i.e. below the strong stochasticity threshold, does not reveal any signature of an intermediate diffusive regime, but rather a direct crossover from ballistic to anomalous regimes [99]. More compelling evidence of the absence of a diffusive regime comes from the study of the harmonic chain with conservative noise [75] with rate \(\varepsilon \rightarrow 0\). It has been found analytically [76] and confirmed numerically [100] that \(J_\textrm{A}(L,\varepsilon )\), exhibits a singular dependence in the form of a divergence of the coefficient \(c_\textrm{A}\) in Eq. (17), \(c_\textrm{A} \approx \varepsilon ^{-1/2}\), which implies that \(J_\textrm{A}\) dominates \(J_\textrm{N}\) for any value of L.
The above reasoning can explain the numerical observation of the apparent normal diffusion observed for asymmetric potentials \(U(x)\ne U(-x)\) [78, 96, 101, 102]. Indeed, if the potential is well approximated by a perturbed Toda one, the crossover to the anomalous regime may occur at prohibitively large sizes. For instance, the paradigmatic FPUT chain is consistent with this scenario [65]. Other studies confirmed that the diffusive regime is indeed a finite-size effect, whereby anomalous behavior is recovered for L large enough [65, 102,103,104].
2.5 Long-range interacting chains
Another ingredient that has been considered in this context is the effect of long-range interactions, i.e. systems in which the interparticle potential decays at large distances r as \( r^{-d-\sigma }\), in dimension d. [105, 106]. The study of this class of problems has a long-standing tradition in equilibrium statistical mechanics, starting from the seminal works by Dyson [107]. Besides the theoretical motivations, there are also experimental examples, notably trapped ion chains, dipolar condensates etc. both classical and quantum [108].
One distinguishing feature is that, for interactions decaying sufficiently slowly with distance, perturbations may propagate with infinite velocities, yielding qualitative differences with respect to their short-ranged counterparts [109, 110]. At nonequilibrium, the dynamics of long-range systems presents metastable states, whose lifetime scales as N [105, 106, 111] and even lack of thermalization upon interaction with a single external bath [112]. As far as transport and hydrodynamics are concerned, non-local effective equations are expected to arise naturally by the non-local nature of couplings. This has also effects on energy transport for open systems interacting with external reservoirs and, more generally, on the way in which the long-range terms couple the system with the environment.
For the class of nonlinear oscillator lattices treated here, there is now a body of evidence that non-Fourier transport would occur, although several issues are still open. Let us first considered the simplest extension of (6) that contains long-range harmonic couplings (see Fig. 2) [113]
where \(\mu \) is a coupling constant. The cases \(\mu >0\) and \(\mu <0\) correspond to ferromagnetic (attractive) and antiferromagnetic (repulsive) interactions, respectively. For a finite, periodic lattice, \(d_{ij}\) identifies the shortest distance between sites i and j
The real exponent \(\sigma \ge -1\) controls the interaction range. In one-dimension, for \(\sigma <0\) the energy is made extensive by the Kac prescription [105] i.e. by introducing the factor
For \(\sigma > 0\), \({{\mathcal {N}}}_\sigma \) attains a constant value for large sizes N and diverges for \(\sigma < 0\), ensuring energy extensivity. Notice that \(\sigma = -1\) corresponds to a mean-field interaction, \(N_{-1}=N\) [114, 115], while in the limit of \(\sigma \rightarrow +\infty \) the case of nearest-neighbor interactions is retrieved.
Schemes of a one-dimensional coupled-oscillator model with single and double-well local potential and long-range interaction decaying as \(d_{ij}^{-1-\sigma } \), \(d_{ij}\) represents the distance between the lattice sites, and the Hamiltonian is given by (18)
Another class of models is the one with nonlinear long-range forces. Two specific examples have been considered in the literature. The first one is a harmonic chain with long-range quartic coupling [116, 117]
The second has instead the form [118, 119]
with \(U=U_{XY}\) [118] and \(U=U_{\textrm{FPUT}}\) [119]. The two models differ in their dispersion relation in the harmonic limit, as obtained by seeking for plane-wave solutions of the form \(q_n\sim \exp (\imath kn-\imath \Omega _\sigma t)\) (for periodic boundary conditions the allowed values of the wave number k are integer multiples of \(2\pi /N\)). In fact, model (21) has the standard, \(\sigma \)-independent acoustic dispersion \(\Omega ^2(k)=4\sin ^2(k/2)\) and finite group velocities. Instead, for (22) the dispersion relations read [120, 121]:
For \(N\rightarrow \infty \) and in the small wavenumber limit, \(\mid k \mid \rightarrow 0\),
As a consequence, the group velocity diverges as \(\mid k\mid ^{\frac{\sigma -2}{2}}\) in the first case, while it is finite in the second one. This result can also be derived from the continuum limit, yielding a fractional wave equation [122]. The case \(\sigma <0\) is even more peculiar, since the spectrum remains discrete in the thermodynamic limit [123] and will not be considered henceforth.
Let us first discuss the case (18), and focus on the so-called weak-long range case, \(\sigma >0\). As far as hydrodynamics is concerned, the main results can be described effectively assuming that the fluctuations of the local energy field
propagates as a Lévy flight. This process is well known as the simplest generalization of the Brownian random walk, yielding anomalous diffusion of an individual particle [124]. More precisely, we assume that the site energies \(h_j\) undergo a stochastic process ruled by the master equation
where \(\lambda \) is a characteristic rate, setting the inverse timescale of the process. Remarkably, this simple model accounts both for the dynamical scaling of structure factors and for the scaling of the energy flux out-of-equilibrium [113]. Large-scale fluctuations of the local energy field display hydrodynamic behavior, which is diffusive for \(\sigma >1\) and superdiffusive for \(0<\sigma <1\) in both the cases with single and double-well local potentials, with either attractive or repulsive couplings. In the superdiffusive case, numerical data and (26) suggest that the energy field follows a fractional diffusion equation of order \(\sigma \), i.e. a non-Fourier heat transport with an anomalous scaling of the energy flux as \(L^{-\sigma }\). Remarkably, in the case of the double-well potential with attractive interaction such behavior of energy fluctuations appears to be insensitive to the phase transition.
In hindsight, the very fact that a Lévy flight model accounts for the large-scale energy fluctuations and transport may appear an obvious consequence that the couplings decay algebraically with the distance. However this is not the case for at least two reasons. First, the correct exponent in (26) must be \(\sigma +2\), which is not trivial a priori. Second, models with the same \(r^{-1-\sigma }\) interactions like (21) and (22) have different dynamical exponents [116, 118, 125]. For instance for the FPUT model, the structure factors at finite energy density display distinct peaks, corresponding to long-wavelength propagating modes, whose dispersion relation is compatible with (24). Also, they display dynamical scaling of the form (12), with a dynamical exponent z that depends weakly on \(\sigma \) in the range \(0<\sigma <2\). The line shapes have a non-trivial functional form and appear somehow independent of \(\sigma \).
In other words, models having the same coupling \(r^{-1-\sigma }\) may belong to different dynamical universality classes, having different hydrodynamics. This conclusion is confirmed also by noting the differences between model (18) and the momentum-exchange model with long-range interactions [126]. It consists of the Hamiltonian (18) with a quadratic pinning potential V perturbed by a random exchange of momenta between the nearest neighbor sites, occurring with a given rate [126]. This model allows for an exact calculation of the exponent \(\delta \) ruling the decay of energy current auto-correlation (and thus the finite-size scaling of the heat flux in the nonequilibrium setup). It turns out that \(\delta \) has a dependence on \(\sigma \) which is different from the nonlinear model described above: for instance, for the momentum-exchange model, superdiffusive transport occurs for \(\frac{1}{2}<\sigma <\frac{3}{2}\) instead of \(0<\sigma <1\). Moreover, the associated fractional diffusion equation in the hydrodynamic limit [127] has a different order. Thus the two models belong to different classes.
The situation is even more complicated for models (21) and (22). The numerical results indicate that the exponent \(\gamma \) of finite-size conductivity depends in a non-trivial way on \(\sigma \) [94, 116], see Fig. 3. An intriguing feature is also that for \(\sigma =1\) the conductivity diverges almost linearly with the system size and the temperature profile has a negligible slope [94, 116]. This ballistic transport regime is unexpected and may perhaps suggest that the models are close to some (yet unknown) integrable limit. To try to rationalize the results so far available, in Fig. 3, we collected the data of the exponent \(\gamma \) as a function of the range exponent \(\sigma \).
Long-range chains: dependence of the thermal conductivity exponent \(\gamma (\sigma )\) on the exponent controlling the interaction range \(\sigma \). Upper panel: case of models momentum-conserving FPUT (21 and (22 taken from [116] and [94]. Lower panel: case with pinning potential (18) taken from [113]; the solid purple line is what predicted from the Levy flight master equation (26). In both panels, the solid green lines are the analytical result for the related momentum-collision model, see [86] for details
At equilibrium, there is also evidence of dynamical scaling of the correlation functions of sound modes, akin to the one seen in the short-range case Eq. (10), but with a \(\sigma \)-dependent dynamical exponent \(z(\sigma )\) [125]. Within the accessible time and size ranges, it is also found that the short-range limit is hardly attained, even for relatively large values of \(\sigma \).
In conclusion, there is plenty of evidence that transport in long-range interacting systems may be anomalous, but a systematic understanding of the different universality classes, akin to the short-range case, is lacking.
2.6 Low-dimensional fluids
So far we have discussed the case of lattice models, mostly in one dimension. To test the generality of the results and their universality, we also discuss the case of low-dimensional fluids. Historically, it is in this context that the long-time tails of correlations were first discovered and studied by mode-coupling approximations [25]. Although molecular dynamics would be the natural choice, we describe here a different approach, that has been recently used to study anomalous transport. The idea is to consider effective stochastic processes capable to mimic particle interaction through random collisions. A prominent example is the Multi-Particle-Collision (MPC) simulation scheme [128], that proved to be very effective for the simulation of the mesoscopic dynamics of polymers in solution, colloidal and complex fluids etc.
In brief, the MPC method consists in partitioning the system of N particles into \(N_\textrm{c}\) cells. The center-of-mass coordinates and velocity in each cell are computed and particle velocities in the cell’s center-of-mass frame are rotated around a random axis. The rotation angles are assigned in such a way that the invariant quantities are locally preserved. All particles are then propagated freely, for a time interval \(\delta t\). Physical details of the interactions can be also included. For instance, energy-dependent collision rates can be considered [42]. Interaction with external reservoirs can be implemented by imposing Maxwellian distributions of velocity and chemical potentials on the thermostatted cells [129], or via thermal walls at the system boundaries [130].
For the case of a one-dimensional MPC fluid, since the conservation laws are the same as say, the FPUT model, we expect it to belong to the same KPZ universality class of anomalous transport [60, 131]. At equilibrium, numerical measurements of dynamical scaling agrees with Eq. (12) both in the strictly 1D [68] than in quasi-one-dimensional case, namely a fluid confined in a box with a relatively large aspect ratio [42]. Possible dimensional crossovers upon changing the aspect-ratio are also demonstrated [42].
Evidence of superdiffusive heat transport is also found in the open setup, where the 1D MPC fluid interacts with two heat reservoirs modeled as thermal walls [130]. In Fig. 4, we report the results of simulations that clearly show anomalous transport in the KPZ universality class for the regime of small enough collision times \(\delta t\) (crosses). Moreover, upon increasing \(\delta t\) one observes a clear crossover from a normal/kinetic regime to an anomalous/hydrodynamic one, above a characteristic size, which can be estimated to be of order \((\delta t)^{3}\). This is in agreement with the scenario presented above for almost-integrable systems [72, 104, 132].
For the more realistic case of a genuine 3D MPC fluid for large aspect ratios of the simulation box, a crossover from 3D to one-dimensional (1D) abnormal behavior of the thermal conductivity occurs [133]. The transition from normal to abnormal transport is well accounted for by the decomposition (17) of the energy current, and the three-regimes scenario described in Sect. 2.4 is again observed in the weakly collisional case, where the mean free path is large enough (i.e. when the frequency of the MPC move is small). This confirms that superdiffusive heat transport persists also for almost 1D fluids over a large range of sizes.
To conclude this overview, we register a growing interest and evidence for anomalous heat transport also in other condensed-matter systems. For instance, the thermal conductivity for one-dimensional electronic fluids has been recently examined [134]. It is argued that at lowest frequencies or longest length scales, the thermal transport is dominated by Lévy flights of low-momentum bosons that lead to a fractional scaling, \(\omega ^{-1/3}\) and \(L^{1/3}\) of heat conductivity with the frequency and system size, respectively.
MPC fluid confined in a 1d box of length L. The MPC collision is performed at regular times steps, separated by a constant time interval of duration \(\delta t\). Particles interact with two thermal walls at temperatures \(T_0=4\), \(T_{L}=2\): when a particle crosses the boundary it is re-injected inside with a new velocity drawn at random from a Maxwellian distribution at the wall temperature. a The energy current J as a function of the box size L for increasing collision times \(\delta t=0.1, 0.5, 1.0, 2.0, 5.0\) and 10 (bottom to top). The upper and the lower dashed lines correspond to the scaling of normal and anomalous transport, respectively. b The heat conductivity \(\kappa =JL/(T_{L}-T_0)\) with the system size L; the dot-dashed blue line is a fit of the data for \(\delta t=10\) with the functional form \(34.2x/(12.2+x)\), suggested by kinetic theory, see Eq. (16)
3 Thermal management and conversion
In this section, we describe some application of the above concepts to achieve control of energy currents, enhanced energy conversion and inverse coupled currents, flowing against applied thermodynamic forces.
3.1 Thermal rectification
Generally speaking, a thermal rectifier (or thermal diode) is a device that allows the heat flow from one end to the other of it, but it inhibits the flow in the opposite direction. While the design of a thermal rectifier [135,136,137,138,139,140,141,142] is fully compatible with the Fourier law, non-Fourier transport may introduce useful features.
Let us first define a suitable rectification coefficient. We consider the heat flow in, say, the x direction, with heat baths imposed at the left and right boundaries of a system, \(T(x=0)=T_1\) and \(T(x=L)=T_2\), respectively. Thermal rectification can occur if there exist some features that break the left-right symmetry of the system. In the case of Fourier transport, we should have a local thermal conductivity that depends on the position x and on the local temperature T(x). Using the Fourier law, we can then write
where \(J_\textrm{f}\) if the forward heat flow (from left to right, under the condition \(T_1>T_2\)) and \(\kappa \) the local thermal conductivity. By solving this equation under the boundary condition \(T(x=L)=T_2\), we can determine \(J_\textrm{f}\). If the boundary conditions are reversed, \(T(x=0)=T_2\) and \(T(x=L)=T_1\), we obtain another dependence on x of local temperature and local thermal conductivity. The resulting backward heat flow \(J_\textrm{b}\) (from right to left) can be different from the forward heat flow, as a result of either inhomogeneity in the material or in the geometry. The rectification coefficient can then be defined as
where \(J_{+}=\textrm{max}\{J_\textrm{f},J_\textrm{b}\}\) and \(J_{-}=\textrm{min}\{J_\textrm{f},J_\textrm{b}\}\).
Summarizing the previous discussion, we need two basic ingredients for thermal rectification: a temperature-dependent thermal conductivity and the breaking of the (left–right) inversion symmetry in the direction of the heat flow. Here, we consider the case of electrical insulators in which heat is only carried by phonons. The two basic ingredients can then be found in simple models of one-dimensional lattices. Let us consider the Hamiltonian
where \(q_i\) denotes the displacement from the equilibrium position of the i-th particle with mass \(m_{i}\) and momentum \(p_{i}\), and \(V_i(q_i)\) is a nonlinear on-site potential. Thermal rectification requires some inhomogeneity in the system, for instance, one could consider segmented chains with different nonlinearities in the different parts, or a mass-graded system. The nonlinearity is needed to obtain a temperature dependence of the phonon bands. In the presence of a thermal gradient, the effective phonon frequencies can depend, for a given position x, on the orientation of the gradient. As a result, one can have either a good matching of the phonon bands at the interfaces between different parts of the material (say, for forward thermal bias, \(T_1>T_2\)), or a mismatch (for backward bias, \(T_1<T_2\)). In the first case, the thermal conduction is expected to be much higher than in the latter. The discussion so far could be carried within the framework of Fourier heat transport, and indeed theoretical models of nonlinear systems which obey the Fourier law have been proposed, for which a rectification factor up to the order of \(10{,}000\%\) has been found.
Besides experimental difficulties (phononic devices [143,144,145,146,147,148,149,150,151] so far are limited to \(f_r\approx 70\%\)), there is a main conceptual limitation. For a system described by the Fourier law, rectification rapidly decays to zero as the size increases. This effect is due to the fact that rectification is a nonlinear phenomenon, which vanishes in the linear response regime. For a given temperature bias, the temperature gradient decreases as the system size increases, and therefore the linear response regime is approached more and more with increasing the system size. To address larger system sizes is, on the other hand, a practical necessity, since it is difficult to apply large temperature biases on small scales.
Non-Fourier transport offers a possibility to solve this problem, by inserting a ballistic channel between the two, anharmonic and asymmetric, leads [152] (see Fig. 5, top left, for a schematic drawing of the model). For instance, one can consider the \(\phi ^4\) lattices, \(V_i(q_i)=\frac{\gamma _i q_i^4}{4}\) in Eq. (29). The overall system consists of \(N_{\textrm{L}}\) (\(N_{\textrm{R}}\)) particles with mass \(m_{\textrm{L}}\) (\(m_{\textrm{R}}\)) and strength of the on-site potential \(\gamma _\textrm{L}\) (\(\gamma _\textrm{R}\)) in the left (right) lead. The two anharmonic leads are connected by a ballistic channel, that is, by a purely harmonic central chain of \(N_\textrm{C}\) particles with mass \(m_\textrm{C}\) and zero on-site potential, \(\gamma _\textrm{C}=0\). The total system size is \(N=N_{\textrm{L}}+N_{\textrm{C}}+N_{\textrm{R}}\).
Top left: schematic drawing of a thermal rectification model based on mass-graded leads, connected by a ballistic channel. Bottom left: boundaries of the effective phonon band as a function of temperature, for lighter masses (\(m=1\), solid red lines) and for heavier masses (\(m=10\), dashed blue lines). Right: rectification factor versus the overall system size N, with ballistic channel (squares) and for the \(\phi ^4-\phi ^4-\phi ^4\) model (triangles), for \(\textrm{max}(T_\textrm{L},T_\textrm{R})=9.5\), \(\textrm{min}(T_\textrm{L},T_\textrm{R})=0.5\), \(N_{\textrm{L}}=N_{\textrm{R}}=10\), \(m_{\textrm{L}}=1\), \(m_{\textrm{C}}=4.5\), \(m_{\textrm{R}}=10\), \(\gamma _{\textrm{L}}=\gamma _{\textrm{R}}=1\), and \(\gamma _{\textrm{C}}=0\) (\(\gamma _{\textrm{C}}=1\)) for the model with (without) ballistic channel. Adapted with permission from [152]. Copyright @ 2018 American Physical Society
The asymmetry needed for heat rectification is here provided by considering a mass-graded system, with \(m_\textrm{L}<m_\textrm{R}\). The mechanism for rectification can be explained in terms of matching/mismatching of the phonon bands for the two leads, when the higher temperature is on the side of the heavier/lighter masses. An effective phonon analysis predicts the phonon spectrum in the band \(\sqrt{1.23\,T^{2/3}/m}\le \omega \le \sqrt{(4+1.23\,T^{2/3})/m}\). This band is shown in the bottom-left panel of Fig. 5. A weak temperature dependence is observed for heavy masses, since in this case the nonlinearity is weak, while the temperature dependence is much stronger for light masses. The phonon bands for the two leads then significantly overlap when the higher temperature is applied to the heavier lead, with band mismatch for the reverse thermal bias configuration. The ballistic channel is then chosen with phonon band that has a significant overlap with the phonon bands of both leads, as it is the case for mass \(m_\textrm{C}\) intermediate between \(m_\textrm{L}\) and \(m_\textrm{R}\).
The advantage of a non-Fourier, ballistic channel is clear from the right panel of Fig. 5, showing the size-dependence of the rectification factor \(f_r\) when the intermediate channel is either diffusive (\(\gamma _\textrm{C}=\gamma _\textrm{L}=\gamma _\textrm{R}\)) or ballistic (\(\gamma _\textrm{C}=0\)). While in the former case (\(\phi ^4-\phi ^4-\phi ^4\) model) the rectification factor rapidly decays with the system size, in the latter case (\(\phi ^4\)-harmonic-\(\phi ^4\) model) the rectification factor is size-independent. Such a result is a consequence of the flat temperature profile in the ballistic channel. That is, the temperature drop happens only in the leads and therefore the temperature gradient, there, is not affected by the length of the ballistic channel. The linear response regime, which would imply no rectification, is therefore never reached, in contrast with the case where the whole system is a \(\phi ^4\) lattice, which obeys the Fourier law.
3.2 Coupled transport
In this section, we discuss the possibilities offered by anomalous heat transport for heat to work conversion.
We consider steady-state transport of two coupled flows, induced by two thermodynamic forces. For concreteness, we focus on thermoelectricity [153,154,155,156], where the two coupled flows are heat and charged particle flow, induced by gradients of temperature and electrochemical potential. However, the discussion that follows could be easily reformulated to other cases, like thermodiffusion, where the flow coupled to heat is neutral particle flow. In thermoelectric devices part of the heat flow is converted into useful work. To characterize the performance of a heat engine, we should consider different features.
First, we define the engine efficiency as the ratio \(\eta =W/Q_\textrm{h}\) of the output work W over the heat \(Q_\textrm{h}\) extracted from the hot reservoir. The second law of thermodynamics tells us that the efficiency is upper bounded by the Carnot efficiency \(\eta _\textrm{C}=1-T_\textrm{c}/T_\textrm{h}\), with \(T_\textrm{h}\) and \(T_\textrm{c}\) temperature of the hot and cold reservoir, coupled to the system (the “working fluid”) where the energy conversion occurs.
Moreover, one should also consider the output power, since an ideal engine approaching the Carnot efficiency for a quasi-static, infinitely slow transformation would be of no practical use. Indeed, the delivered power would vanish in that limit.
Finally, also the constancy in the power supplied by the engine is important, and power fluctuations are expected to play an important role when dealing with nanoscale engines.
Note that, while we focus our discussion on power production, one could equally well consider refrigeration, after an appropriate reformulation of the problem, where the coefficient of performance (heat extracted from the cold reservoir over the absorbed power) and the cooling power are considered as key quantities.
Thermoelectric transport can be conveniently formulated within linear response. Since linear response is based on the expansion of currents, to linear order, around local equilibrium conditions, the validity of such approach requires that the temperature drop \(\Delta T\) and the electrochemical potential drop \(\Delta \mu \) on the scale of the relaxation length are such that \(\Delta T\ll T\) and \(\Delta \mu \ll k_\textrm{B} T\), where \(k_\textrm{B}\) is Boltzmann constant and T the local temperature. In thermoelectric materials at room temperature, electrons are typically thermalized by inelastic electron–phonon scattering and the relaxation length is of some tens of nanometers. In this case, linear response is usually a good approximation, even though the temperature differences between the two reservoirs can be large. For instance, in the proposed application of the automotive industry to generate electricity from the waste heat in a vehicle’s exhaust pipe, the hot reservoir (the exhaust gases) is at temperature \(T_\textrm{h}\approx \) 600–700 K, while the cold reservoir (the environment) is at room temperature, \(T_\textrm{c}\approx \) 270–300 K. In spite of the large temperature difference, linear response can be used, since the temperature drop from \(T_\textrm{h}\) to \(T_\textrm{c}\) takes place on the scale of a few millimeters, and therefore on the scale of the relaxation length (around 10 nm) the temperature drop is of the order of 0.003 K, much smaller than the local temperature.
Within linear response, the relation between currents and generalized forces is linear [157, 158]. In particular, for thermoelectric transport, we have
where \(J_e\) is the electric current density, \(J_u\) is the energy current density, and the conjugated thermodynamic forces are \({\mathcal {F}}_e=-\nabla (\mu /eT)\) and \({\mathcal {F}}_u=\nabla (1/T)\), where \(\mu \) is the electrochemical potential and e is the electron charge. The coefficients \(L_{ab}\) (\(a,b=e,u\)) are known as kinetic or Onsager coefficients. Note that the heat current is \(J_{h}=J_u-(\mu /e) J_e\), namely it is the difference between the total energy current \(J_u\) and the “ordered” part of it, i.e. the electrochemical potential energy current \((\mu /e) J_e\).
The kinetic coefficients \(L_{ab}\) are related to the more familiar thermoelectric transport coefficients: the electrical conductivity \(\sigma \), the thermal conductivity \(\kappa \), the thermopower (or Seebeck coefficient) S, and the Peltier coefficient \(\Pi \):
For systems with time reversal symmetry, due to the Onsager reciprocal relation \(L_{eu}=L_{ue}\), and therefore \(\Pi =TS\).
When the above Onsager relation is valid, the thermoelectric performance is governed by the thermoelectric figure of merit
Thermodynamics imposes only a lower bound on the figure of merit: \(ZT\ge 0\). The thermoelectric conversion efficiency is a monotonic increasing function of ZT, with \(\eta =0\) at \(ZT=0\) and \(\eta \rightarrow \eta _\textrm{C}\) in the limit \(ZT\rightarrow \infty \). Nowadays, most efficient thermoelectric devices operate at around \(ZT \approx 1\), corresponding to a maximum efficiency about \(15\%\) of the Carnot efficiency. On the other hand, it is generally accepted that \(ZT>\) 3–5 is the target value for a commercially competing thermoelectric technology. Indeed, reaching these values would yield a maximum efficiency about \(40\%\) of the Carnot efficiency, thus making thermoelectric devices on par with other widely used heat engines. It is an elusive challenge to increase the thermoelectric efficiency, since the transport coefficients \(S,\sigma ,\kappa \) are generally interdependent. For instance, the phenomenological Wiedemann–Franz law states that \(\sigma \) and the electronic contribution \(\kappa _e\) to \(\kappa \) are proportional, so that it is not possible to independently increase \(\sigma \) and decrease \(\kappa \), as desirable to enhance the figure of merit ZT. It is therefore of great importance to understand which physical mechanisms might allow to independently control the above transport coefficients, and in particular to violate the Wiedemann–Franz law. Note that the thermal conductivity \(\kappa =\kappa _e+\kappa _p\) also includes the contribution \(\kappa _p\) from phonons and photons, so that improving the efficiency of energy conversion for electrons by itself does not guarantee a high ZT. At the same time, one should be able to manipulate phonon transport to reduce the overall thermal conductivity.
In the case of non-integrable, momentum-conserving systems, the thermal conductivity \(\kappa \) diverges sub-ballistically with the system size L. On the other hand, a theoretical argument [159] predicts that in such systems the electrical conductivity is ballistic, that is, \(\sigma \propto L\), and the Seebeck saturates with the system size. This leads to a blatant violation of the Wiedemann–Franz law, since \(\sigma /\kappa \rightarrow \infty \) in the thermodynamic limit \(L\rightarrow \infty \). At the same time, since \(S\sim L^0\), also ZT diverges.
Such prediction has been confirmed in several momentum-conserving models: in a diatomic chain of hard-point colliding particles [159], in a two-dimensional system [129], with the dynamics simulated by the MPC method discussed in Sect. 2.6 (see Fig. 6, left), and in a one-dimensional gas of particles with screened (nearest neighbour) Coulomb interaction [160]. In all these models, collisions are elastic. On the other hand, when noise breaking momentum conservation is added, ZT becomes asymptotically independent of the system size, as expected for a diffusive transport regime. However, when noise is weak ZT can grow up to large values before saturating (see the right panel of Fig. 6).
Left: Thermoelectric transport coefficients for the two-dimensional MPC model as a function of the system size. The dashed lines correspond to the theoretical predictions \(\sigma \sim L\), \(\kappa \sim \log L\), \(S=3/2\), and \(ZT\sim L/\log L\). Right: ZT vs. L, with the above theoretical expectation (dashed line) compared with simulation where a stochastic noise breaking momentum conservation is added, of strength growing from top to bottom. Adapted with permission from [129]. Copyright @ 2014 Institute of Physics
Besides efficiency, also power and constancy deserve a close inspection. Indeed, an ideal heat engine should operate as close as possible to the Carnot efficiency, deliver large power and exhibit small fluctuations. A trade-off between these three desiderata of a heat engine can be obtained for a broad class of systems on the basis of thermodynamic uncertainty relations (TURs) (see [161, 162] for perspective papers on TURs). More precisely, we refer to classical systems described by thermodynamically consistent rate equations on a discrete set of states or modeled with overdamped Langevin dynamics, under steady-state conditions and with time-reversal symmetry. In that case, from the TUR for the “work current”, namely for power, it is possible to show that [163]
where the (steady-state) power fluctuations are given by
Here P(t) is the mean delivered power up to time t. Note that, since P(t) converges for \(t\rightarrow \infty \) to P as \(1/\sqrt{t}\), an additional factor of t in (37) is needed to obtain a finite limit for \(\Delta _P\). Bound (36) tells us that it is not possible to go arbitrarily close to the Carnot efficiency while keeping at the same time finite power and non-diverging fluctuations.
Note that non-integrable, momentum-conserving systems, for which heat conductivity is anomalous, can achieve the bound \({\mathcal {Q}}=\frac{1}{2}\) when approaching the Carnot efficiency [164]. On the other hand, for (classical and quantum) systems described by scattering theory the upper bound for \(\eta \rightarrow \eta _\textrm{C}\) is lower, \({\mathcal {Q}}=\frac{3}{8}\) [164]. Therefore, interactions are necessary to achieve the optimal performance of a steady-state heat engine, as it is the concretely the case for momentum-conserving systems.
3.3 Inverse coupled currents
The usual way to build a thermoelectric heat-engine is to construct a thermocouple from two thermoelectric materials, the two ideally having opposite thermoelectric responses. The reason is that in the Seebeck effect a temperature difference pushes charge carriers to the cold side of the material, so that a voltage is induced. In the case the flow is due to electrons, as in n-type semiconductors, the Seebeck coefficient S is negative. On the other hand, in p-type semiconductors, the flow is due to holes, positively charged, and so S is positive. As a consequence, in a thermocouple a circulating current is established, and a load attached to the circuit can turn the electrical power into some other kind of work (for instance the load could be a motor which generates mechanical work).
Momentum-conserving systems offer a conceptually appealing possibility to have systems with opposite sign of the Seebeck coefficient. A negative Seebeck is here quite counterintuitive since it implies the possibility of a particle current against thermodynamic forces, a possibility, however, not excluded by thermodynamics for coupled flows. For a single flow, a response to an applied static force \({\mathcal {F}}>0\) by generating a current \(J<0\) against that force is known as absolute negative mobility (ANM). Such possibility is excluded around a thermal equilibrium state [165, 166], otherwise ANM could be exploited to construct a perpetuum mobile of the second kind, with a single heat bath performing work. That is to say, the entropy production rate \(\dot{{\mathscr {S}}}=J{\mathcal {F}}\) would be negative, against the second law of thermodynamics. Therefore, ANM can appear only in nonequilibrium setups, for instance in relation to particle separation [167, 168], self-propulsion [169], tracer dynamics in a laminar flow [170], and also experimentally in semiconductor superlattices [171], micro-fluidic systems [172], and Josephson junctions [173].
Conversely, the above limitation does not apply for coupled flows, and it is indeed possible to have inverse currents in coupled transport [174, 175] (ICC). Referring again for concreteness to thermoelectricity, the positivity of the entropy production rate \(\dot{{\mathscr {S}}}=J_e{\mathcal {F}}_e+J_u{\mathcal {F}}_u\) (\({\mathcal {F}}_e,{\mathcal {F}}_u>0\)) can be fulfilled even though one of the two induced currents has sign opposite to both forces (say, \(J_e > 0\) and \(J_u < 0\)). Within linear response, one needs negative Onsager cross-coefficients [53, 174, 175], a possibility not excluded by thermodynamics. Indeed, since \(J_e =L_{ee} {\mathcal {F}}_e + L_{eu} {\mathcal {F}}_u\), and from the positivity of entropy production \(L_{ee}\ge 0\), it is necessary that \(L_{eu}<0\).
We stress that the ICC phenomenon should not be confused with standard thermoelectric transport, where the two thermodynamic forces have opposite sign instead. There, the motion of particles against an electrochemical potential difference is possible thanks to a temperature difference. In ICC an inverse particle current is obtained, very counterintuitively, when particles move against both the temperature and the concentration gradient (see the top left panel of Fig. 7).
Top left: Schematic drawing of ICC, where either particle or heat flow is against both the temperature and the concentration gradient. Bottom left: Sketch of an ICC-based heat engine, consisting of two channels, between two reservoirs at different temperatures \(T_\textrm{L}\) and \(T_\textrm{R}\) (chemical potentials self-adapt to values \(\mu _\textrm{L}\) and \(\mu _\textrm{R}\) in the steady-state regime). For visualization purposes, the two species of charged particles in each channel are represented by bullets and rods, respectively. A circular current of bullets can form and work can be extracted by the applied potentials \(U_\textrm{A}\) and \(U_\textrm{B}\). Right: dependence of the figure of merit YT on the system size \(L=L_\textrm{A} =L_\textrm{B}\) for barrier height \(h=h_\textrm{A} =h_\textrm{B} =0.5,1.0\), and 1.5. Adapted with permission from [176]
Momentum-conserving systems offer an appealing possibility to realize ICC in a Hamiltonian system, which can be seen as a classical version of the Lieb–Liniger model [177, 178]:
where \(m_i\in \{m,M\}\), \(V(x)=h\) for \(x \le |r|\) and \(V(x)=0\) otherwise, with \(h\ge 0\) being the height of the potential barrier (hereafter we set \(r=0\)). Note that for \(h=0\), all particles move freely and the system is integrable, while in the other limiting case \(h\rightarrow \infty \), the system reduces to the nonintegrable two-species hard-core gas, a paradigmatic model in the study of anomalous one-dimensional heat transport.
We can understand the fact that the cross-coefficient \(L_{eu}\) is negative as follows. If we set \({\mathcal {F}}_e=0\) and \({\mathcal {F}}_u>0\), then the probability for two particles to cross each other is higher when the light particle is closer to the hot reservoir and the heavy particle is closer to the cold reservoir. In this case, the relative velocity of the two particles is on average higher than in the opposite configuration. Hence, it is more probable that the relative velocity of the two particles injected by the baths is sufficient to overcome the potential barrier. This creates an unbalance in the particle density for the two species. As the temperature difference between the two reservoirs is increased, this mechanism can even lead to a phase separation [179, 180].
Thanks to the ICC effect, it is possible to build a two-channel heat engine [176] where, as in a thermocouple, a stationary circular motion of particles is established and maintained by an applied temperature bias (see Fig. 7, bottom left). In the channels the particles of mass \(M_\textrm{A}>m\) (in channel A) and \(M_\textrm{B}<m\) (in channel B), represented for visualization purposes as rods, are reflected back when they hit a channel boundary, with a newly assigned velocity sampled from the equilibrium, thermal distribution determined by the temperature of the reservoir in contact with that boundary. On the other hand, particles of mass m (depicted as bullets) can enter the reservoirs, which in turn inject bullets into the channels with rates and energy distribution determined by their temperatures and densities. Thanks to this effect, it is possible to make the bullets flow inversely in one channel, say, channel B, by setting \(M_\textrm{B}<m\), so that a clockwise-circulating bullet current through the whole system is created. Work can then be extracted by applying two external bias voltages \(U_\textrm{A}\) and \(U_\textrm{B}\) on the two channels, respectively (for instance, we could use a portion of the kinetic energy of the circulating particles to set to rotation lifting wheels). The net effect is that the engine converts a portion of the heat flowing from the hot to the cold reservoir into work, in a very efficient way. Indeed, numerical simulations and a linear response analysis suggest that the Carnot efficiency can be achieved, under suitable conditions, in the thermodynamic limit.
Note that within linear response engine efficiency is a monotonously growing function of the figure of merit YT [181, 182]:
where \(\sigma _i\), \(\kappa _i\), \(S_i\), and \(L_i\) stand for electrical conductivity, thermal conductivity, thermopower, and length of channel i (\(i=A,B\)). Thermodynamics requires \(YT\ge 0\), with the efficiency of heat to work conversion vanishing for \(YT=0\) and achieving the Carnot efficiency for \(YT\rightarrow \infty \). Numerical simulations suggest that the Carnot limit can be achieved for \(L=L_{A}=L_{B}\), \(h_{A}=h_{B}\sim 1/\sqrt{L}\), in the thermodynamic limit \(L\rightarrow \infty \), thanks to the interplay between ballistic particle transport and anomalous, sub-ballistic heat transport, and to the opposite sign of the Seebeck coefficients in the two channels, with the negative Seebeck coefficient in the channel with ICC.
4 Atomistic simulations
Since the 1990 s, the developments in the fabrication and characterization of nanostructures have provided the opportunity to test experimentally the predictions of statistical physics models. Suitable one-dimensional systems to probe anomalous heat transport are nanotubes, nanowires, and polymer fibers. Graphene, hexagonal boron nitride, exfoliated transition metal dichalcogenide monolayers, and thin semiconductor membranes have been considered to study thermal transport in two-dimensional systems, as well as possible platform to implement thermal rectification concepts [141].
However, it is difficult to reproduce the physics of ideal models in experiments, the direct interpretation of which is often arduous. Atomistic simulations provide a much-needed bridge between models and experiments. These simulations can entail the specific properties of actual materials and realistic features, such as defects, surface features, and contacts while allowing a detailed insight into the microscopic mechanisms of thermal transport. In fact, atomistic modeling has been successfully employed both to predict the behavior of nanostructures and to interpret experiments.
In this section, we review the contributions of atomistic simulations to the understanding of the aspects non-Fourier heat transport discussed in the previous sections. After some methodological considerations, we address the diverging thermal conductivity in one- and two-dimensional materials, and thermal rectification. Rather than trying to list all the systems that have been studied by molecular simulations, we focus on those closer to statistical models and most likely to exhibit anomalous properties. Further information about simulations of heat transport in nanostructures may be found in [183].
4.1 Molecular simulation methods
Atomistic methods to simulate thermal transport can be classified into two categories: molecular dynamics (MD) and lattice dynamics (LD). Transport coefficients, such as thermal conductivity, can be computed by MD either from the fluctuation of currents at equilibrium (EMD) or, directly, from non-equilibrium (NEMD) simulations. In the former case, the thermal conductivity of a system of volume V is obtained as the infinite time limit of the Green–Kubo integral of the heat current auto-correlation function:
where \(\alpha ,\beta \) are the Cartesian components of the heat current vector J. EMD applies to periodically replicated systems in the bulk limit. Non-Fourier transport is characterized by a slow decay of \(\langle J(t)J(0)\rangle \propto t^{-(1-\delta )}\), i.e. \(\delta \ge 0\) (see Sect. 2). Hence, proving non-Fourier thermal transport by EMD involves probing the long-time tail of correlation functions, which are affected by large statistical uncertainties. This problem is further aggravated by the poor ergodicity of most low-dimensional systems. This issue may be circumvented by running several statistically independent replicas of the same system.
NEMD and reverse-NEMD [184, 185] methods are similar to actual experiments: a system of finite length in the transport direction is connected to two thermal baths at different temperatures. The evolution of the system is simulated until the energy flux (J) from the hot to the cold reservoir becomes stationary. When transport is diffusive at stationary conditions \(\kappa \) may be estimated directly from Fourier’s law as \(\kappa =-J/\nabla T\) by estimating \(\nabla T\) from the temperature profile. In fact, as one normally simulates systems from several nanometers up to at most 10 \(\upmu \)m, the temperature profile is often nonlinear. In these cases, one should calculate the Kapitza conductance of finite-length (L) systems as \(G(L)=J/\Delta T\), where \(\Delta T\) is the temperature difference between the two thermal baths, and estimate the length-dependent thermal conductivity as \(\kappa (L)=G\cdot L\) [186]. The results of finite-size simulations cannot be easily extrapolated to the infinite size limit so proving the divergence of \(\kappa \) of realistic materials through NEMD is a deceptive task [187]. In turn, as a non-perturbative method, NEMD is ideal to probe non-linear effects, such as thermal rectification. There is a variety of algorithms, thermostats, to control either the temperature of the thermal reservoirs in direct NEMD or the heat current in reverse NEMD. Whereas in the diffusive transport regime in three-dimensional materials different approaches to NEMD are generally equivalent, the choice of the algorithm becomes critical in low-dimensional systems, especially concerning ergodicity [186, 188].
An efficient alternative way of computing thermal transport in the MD framework is the so-called approach-to-equilibrium MD (AEMD) [189]. AEMD consists of preparing the system out of equilibrium with two regions at different temperatures and monitoring the relaxation to equilibrium. In diffusive conditions, the temperature difference between the hot and cold regions should decay exponentially following the heat equation, and the thermal diffusivity is proportional to the relaxation time. Size effects in this approach are similar to NEMD.
Taking care of the above-mentioned technical precautions, EMD and NEMD approaches are complementary and provide a versatile framework to perform numerical thermal transport experiments. However, the classical nature of MD limits the direct comparison to experiments when quantum effects matter, i.e. when the temperature is lower than the Debye temperature, \(\Theta _D\) of the system. For example, \(\Theta _D > 1500\) K for carbon-based materials and \(\sim 600\) K for silicon. While quantum corrections can be implemented in NEMD simulations with spectral decomposition [190], lattice dynamics and the Boltzmann transport equation (LD-BTE) offer a more natural route to compute quantum phonon transport in solids [16, 191, 192]. This approach consists of treating the normal modes of a solid as a gas of quantum quasi-particles that diffuse according to the Boltzmann equation at stationary conditions:
where \(n_i(q)\) and \(\vec {v}_i(q)\) are the populations and group velocities of mode i at wavevector q and T is the temperature. The right-hand side of Eq. (41) can be expressed in terms of a tensor, \(\Gamma \), that encompasses both extrinsic, e.g. isotope and boundary scattering, and intrinsic scattering multi-phonon scattering processes. The latter are usually approximated considering three-phonon processes only, but recent works have highlighted the impact of higher-order four-phonon processes, especially in high thermal conductivity materials [193, 194]. The solution of Eq. (41) gives an expression for the thermal conductivity
in terms of the heat capacity \(c_i(q)\), group velocity \(v_i(q)\) and mean free path \(\lambda ^{(\beta )}_i(q)\) of the renormalized phonon modes [195], also called relaxons [196] A major advantage of LD-BTE is that it offers a direct evaluation of the contribution of each mode to the thermal conductivity and it easily allows one to identify which phonon may lead to anomalous heat transport in the extended size limit. Yet, atomistic LD-BTE is rarely used to probe anomalous transport, and the comparison with MD, potentially very insightful, is often challenging [197].
4.2 Anomalous transport in one-dimensional systems
Molecular dynamics simulations of isolated polymer chains: a Green–Kubo running integral of polyethylene (PE) with a different number of units (uc); b extrapolated thermal conductivity (TC) and thermal conductance (G) of PE chain adapted with permission from [198]; c NEMD results for various polymer chains between 1 nm and 1 \(\upmu \)m-long exhibiting critical exponents \(\gamma \sim 0.4\) adapted with permission from [199]; d diverging \(\kappa \) for PEDOT with \(\gamma \sim 0.5\), adapted with permission from [200]
Isolated polymer chains
Isolated polymer chains are the systems that most closely resemble one-dimensional models, such as the FPUT model. While in their bulk form polymer plastics have low thermal conductivity (\(\kappa < 0.5\) Wm\(^{-1}\)K\(^{-1}\) for polyethylene (PE) at room temperature), early simulations suggested that single polymer chains can have substantially higher conductivity [201]. Realistic EMD simulations predicted a very high thermal conductivity, above 100 Wm\(^{-1}\)K\(^{-1}\) for a single PE chain longer than 10 nm, and possibly diverging \(\kappa (L)\) in the infinite-length limit [198]. The raw data from these simulations, reported in Fig. 8a, show that in different runs of the same system the integral in Eq. (40) appears to either diverge or converge depending on the initial conditions. The thermal conductivity of the infinite PE chain would diverge with length under the assumption that all the four acoustic modes would have diverging mean free path. In turn, \(\kappa (L)\) would saturate if one uses a fitted finite value for the relaxation time of these modes, as obtained from the runs in which the Green–Kubo integral converges. Further simulations show that increasing the dimensionality of the system to 2D (thin films) and 3D (bulk) suppresses the anomalous transport behavior [202]. Similarly, at the single molecule level, finite-length fully stretched alkane chains exhibit ballistic transport up to several tens of units [203], but their conductance is reduced introducing kinks by bending [204].
NEMD simulations of 1D polymers of several different kinds consistently report \(\kappa \propto L^\gamma \) divergence for length up to 1 \(\upmu \)m, with \(\gamma \gtrsim 0.4\) [199], in good agreement with kinetic theory predictions for the FPUT-\(\beta \) model [79,80,81,82]. Crnjar et al. investigated anomalous heat transport in poly-3,4ethylenedioxythiophene (PEDOT) 1D chain by AEMD [200]. These simulations show a power-law divergence of \(\kappa (L)\) with exponent \(\gamma \sim 0.5\), possibly corresponding to a new universality class. The PEDOT models are up to 7.5 \(\upmu \)m long, about one order of magnitude longer than previous in NEMD numerical experiments. It is nevertheless not proven that such length is sufficient obtain a well-converged estimate of the critical exponents, as shown by systematic studies of size effects in model systems [73]. EMD simulations of PEDOT show similar behavior as for PE: for some trajectories the Green–Kubo integral (see Eq. (40)) reaches a constant value, while for others it diverges. In general, these works suggest anomalous thermal transport in 1D polymer chains with critical exponents larger than 1/3. While it is unlikely that measurements will confirm or refute this hypothesis, these simulations have suggested an effective approach to obtain high-thermal conductivity polymeric materials by drawing PE fibers, so that the PE chains are aligned and stretched as in the ideal models [205].
Carbon nanotubes
Readily available and much easier to manipulate than polymer chains, carbon nanotubes (CNT) have been among experimentalists’ favorite systems to test anomalous heat transport. After the first measurements reporting extremely high \(\kappa \) in CNTs [206,207,208], several studies tried to assess the thermal conductivity of carbon nanotubes using either MD or LD simulations [58, 209,210,211,212,213,214,215,216,217,218,219,220,221]. Early works confirm the high thermal conductivity observed in experiments. Some of them explicitly address the possibility of anomalous transport, but they fundamentally disagree on the convergence of \(\kappa \) with length. As shown in Table 1, most EMD simulations suggest that the thermal conductivity should be finite, based on the convergence of the Green–Kubo integral. In turn, most NEMD simulations show that \(\kappa \) keeps growing up to lengths of several \(\upmu \)m. As in the case of polymer chains, this uncertain scenario results from the difficulty of converging MD simulations of nonergodic low-dimensional systems, and the sensitivity of the results on specific methodological choices [222]. In any case, both NEMD and AEMD results show anomalous transport—between ballistic and diffusive—in CNTs up to several microns in length. Ray and Limmer [58] showed that the time evolution of temperature perturbations (as in AEMD) and temperature profiles in NEMD agree with those predicted by a Levy walk model, which is non-diffusive, and the thermal conductivity of CNTs with \(L<2~\upmu \)m diverges as \(\kappa \propto L^{1/2}\). This result is supported by the analysis of heat flux fluctuations at equilibrium in finite-length systems, suggesting that \(\kappa \) divergence is not produced by large temperature gradients.
The picture emerging from LD-BTE works is also inconclusive: early calculations showed convergent \(\kappa \) if higher-order anharmonic processes are explicitly accounted for [211]. However, the same authors eventually suggested that \(\kappa \) may converge only when a cutoff to the propagation of low-frequency phonon modes is imposed [225]. These calculations, however, were carried out using a self-consistent solution of the BTE, which has convergence issues when the scattering tensor in the right-hand side of Eq. (41) is non-diagonally dominant [192]. From these works, it is also clear that solving the LD-BTE in the relaxation time approximation (RTA) does not give the correct physical picture of heat transport in either CNTs or any other low-dimensional system.
Exploring the dependence of \(\kappa \) on the CNT diameter, d, both MD and LD-BTE calculations showed that, for a given length, \(\kappa \) is higher for thinner CNTs [220, 226, 227]. As CNTs are not strictly speaking 1D systems, one may argue that the smaller their diameter the closer to an actual 1D system. Ref. [226] showed that this trend is non-monotonic, as \(\kappa \) reaches a minimum for \(d\sim 2\) nm, and then slowly rises toward the limit thermal conductivity of graphene.
While the estimates of CNTs \(\kappa \) by numerical simulations are in the same ballpark of thousands Wm\(^{-1}\)K\(^{-1}\) at room temperature, there is seldom any quantitative agreement among MD and LD-BTE calculations. A couple of recent works have addressed this issue using consistent systems and simulation control parameters for both MD and LD-BTE [227, 228]. These LD-BTE calculations suggest that transport is non-diffusive up to lengths of the order of \(\sim \)1 mm, but \(\kappa (L)\) would probably saturate to a finite value. This determination is however based on the calculation of phonon mean free paths at extremely short wavenumbers, which is very sensitive to numerical errors [229, 230]. To date, BTE cannot be considered conclusive as for the value of the infinite-length limit thermal conductivity of CNTs. Figure 9b highlights the numerical sensitivity of BTE calculations in the long wavelength limit. Bruns et al. also highlighted discrepancies between NEMD and LD-BTE [227]. The main source of these discrepancies is the use of quantum statistics in BTE, while NEMD is Newtonian. If classical statistics is used in the BTE [195] and the boundary conditions for the finite-length systems are applied correctly [231], the NEMD and BTE agree well for nanotubes up to 10 \(\upmu \)m long. Furthermore, EMD simulations converge to a value that is higher than the highest NEMD estimate of \(\kappa \) for \(L \sim ~10\ \upmu \)m, which makes the two methods substantially agree (Fig. 9a) [228].
a Thermal conductivity of a (10,0) CNT from the Boltzmann transport equation (BTE) and equilibrium and nonequilibrium molecular dynamics (EMD, NEMD) simulations as a function of length. The insert shows the convergence of the Green–Kubo integral from an ensemble of EMD runs [228]. b Lifetimes of the flexural and torsional acoustic phonon modes of the same CNT from BTE and either analytical or numerical interatomic force constants. The dashed lines indicate the power law for diverging contribution to \(\kappa \) in the limit of vanishing wavevector, adapted with permission from [229, 230]
On the one hand, the analysis of phonon lifetimes from modal analysis of MD trajectories and BTE calculations indicates that the phonons that may lead to anomalous transport are the two flexural acoustic modes (Fig. 9b). On the other hand, if the atomic coordinates perpendicular to the CNT axis are constrained, the system is left with only the longitudinal acoustic mode and its thermal conductivity is predicted to diverge as \(\kappa \propto L^\alpha \), with \(\alpha \sim 0.45\) [228]. A similar effect may be achieved by applying tensile strain to the CNT, for which BTE calculations predict superdiffusive transport [232].
4.3 Non-Fourier transport in 2D materials
Graphene and hexagonal boron nitride (h-BN) are one-atom thin rigid sheets, thus realizing in the material world the equivalent of two-dimensional lattice models. For this reason, thermal transport in graphene, and to a lesser extent in h-BN, has been intensively investigated to unravel anomalous conduction both by experiments and simulations [233]. As in the case of CNTs, NEMD simulations of graphene do not usually manage to reach saturation of the thermal conductivity, due to their inherent limitation in size and time scales. Large-scale NEMD up to \(10^7\) atoms showed that the thermal conductivity of graphene does not saturate for patches up to several \(\upmu \)m long in very good agreement with experimental measurements [234]. In the length range considered by this work, \(\kappa \propto \log (L)\), as predicted for 2D lattice models [41], thus supporting the hypothesis of anomalous transport. Logarithmic divergence of \(\kappa \) was observed in both NEMD and AEMD simulations on graphene with \(L<2~\upmu \)m [58]. However, further extending the size of the graphene patches to \(L\sim 100\ \upmu \)m, shows evidence of \(\kappa \) saturation [235].
a Thermal conductivity of graphene as a function of temperature and length computed solving the BTE with ab initio interatomic force constants (adapted with permission from [236]. Copyright 2014, American Chemical Society). b Decomposition of the thermal conductivity in in-plane and out-of-plane contributions for unstrained and strained graphene from molecular dynamics simulations (adapted with permission from [237])
In fact, both EMD simulations with empirical potentials [237, 238], and ab initio lattice dynamics BTE calculations [196, 236, 239] confirm that the extended limit of the thermal conductivity is finite. BTE calculations give a quantitative estimate of the bulk thermal conductivity of graphene as a function of both length and temperature in very good quantitative agreement with experiments (Fig. 10a), and they provide in-depth insight into the transport mechanism [236]. At room temperature, heat transport is superdiffusive over lengths of the order of 1 mm, as the main heat carriers are collective phonon excitations with mean free paths that extend up to 100 \(\upmu \)m. This collective effect, equivalent to Poiseuille flow in a fluid, is enhanced in low-dimensional materials, due to the reduced phase space for phonon scattering [196, 239].
The decomposition of the thermal conductivity of graphene into in-plane (\(\kappa _{\textrm{in}}\)) and out-of-plane (\(\kappa _{\textrm{out}}\)) from MD simulations at room temperature shows that the relative contribution depends on the length of the graphene patch (Fig. 10b). \(\kappa _{\textrm{in}}\) converges at relatively short length \(L\sim 1\ \upmu \)m, while \(\kappa _{\textrm{out}}\) keeps increasing up to 10 \(\upmu \)m. Remarkably, these simulations predict that strained graphene would exhibit divergent thermal conductivity, and \(\kappa _{\textrm{out}}\), i.e. the flexural modes, would be responsible for the divergence of \(\kappa (L)\) [237]. This mechanism is analogous to the one discussed for strained CNT in the previous section. It is worth noting that some BTE calculations support the divergence of \(\kappa \) in strained graphene [240, 241], others suggest that strain would reduce \(\kappa \), thus in stark disagreement with MD [196, 236]. The thermal conductivity of strained graphene remains an open issue.
4.4 Ballistic-to-diffusive transport regime
Fourier’s law applies to the diffusive transport regime, which generally occurs in extended materials. However, regardless of their dimensionality, thermal transport through systems of finite size is ballistic when the mean free path of the heat carriers exceeds the distance between the heat baths. From measurements and simulations of nanoscale systems, an intermediate transport regime has emerged, denoted as ballistic-to-diffusive, superdiffusive, or nanoscale transport regime, in which the thermal conductivity appears to be size-dependent [242, 243]. As discussed in the previous sections, in this regime the thermal conductivity depends on the length of the system along the transport direction. This length may extend to several millimeters for low-dimensional nanostructures, but superdiffusive transport has been observed over \(\upmu \)m lengths also for bulk systems at room temperature e.g. crystalline silicon [244], and even in the cross-plane direction of layered materials stemming from unexpectedly long heat carrier mean free paths [245, 246]. It is widely accepted that the superdiffusive regime emerges from the wide range of heat carriers’ mean free paths, which can be accurately obtained from the exact solution of the phonon BTE at the microscopic level. [192] However, it is a matter of debate whether Fourier’s law can be applied to model transport at the nanoscale in ballistic-to-diffusive conditions.
Extending the work by Chen and Zeng [247], Maassen, Lundstrom, and coworkers [231, 248, 249] derived the Fourier’s law for finite-length systems from the BTE by renouncing the assumption of local thermodynamic equilibrium, and applying physically correct boundary conditions of the forward and backward phonon fluxes at the two contacts. Assuming perfectly thermalizing boundary conditions, this approach leads to temperature jumps at the contacts, which approximates consistently the temperature profiles computed in NEMD simulations [188]. Remarkably, one can prove that for a model system with a single mean-free-path (\(\lambda \)) independent on phonon frequency, the thermal conductivity over length \(L<\lambda \) is the same as the bulk thermal conductivity, and the apparent reduction of \(\kappa (L)\) stems from a reduction of the net phonon flux. In general, this approach describes correctly both ballistic effects and the diffusive regime, thus, in principle, it can be applied at all length scales. However, this picture is an approximation, which does not take into account hydrodynamic effects.
Hydrodynamic phonon transport effects, such as Poiseuille heat flow and second sound were observed in crystals at cryogenic conditions as early as the 1960 s. Whereas diffusive (Fourier) transport is controlled by momentum dissipating umklapp scattering processes, hydrodynamic effects emerge from momentum conserving normal scattering processes. The latter prevails at low temperatures, and in materials in which phonon dispersion relations limit the number of umklapp scattering processes. For this reason, phonon hydrodynamics was assumed to have a limited impact until recent experiments on heat transport in the nanoscale regime. In fact, the exact solution of the microscopic BTE, Eq. (41), highlighted the contribution of collective hydrodynamic effects to heat transport in two-dimensional materials [196, 239]. Subsequent work showed that hydrodynamics plays a significant role not only in low-dimensional systems or at very low temperatures, but also in bulk materials at non-cryogenic temperatures [192]. Poiseuille flow and second sound cannot be described by the macroscopic Fourier’s equation, and efforts have been made to generalize the heat equation to account for hydrodynamic effects.
In the limit of weak crystal momentum dissipation, Guyer and Krumhansl derived a steady-state solution of the linearized BTE that can be seen as a generalization of the Fourier’s law and reads [250]:
with \(\alpha = 2\). This equation is characterized by a collective non-local length l that defines the length-scale \(L\sim l\) at which phonon hydrodynamics impacts heat transport. Equation (43) can be obtained more generally through the Chapman–Enskog first-order expansion solution to the BTE with the relaxation time approximation [251].
Similarly to \(\kappa \), the hydrodynamic length l can be expressed in terms of microscopic phonon properties by separating the contributions to the phonon lifetime from normal (\(\tau _\textrm{N}\)) and umklapp (\(\tau _\textrm{U}\)) scattering processes. In the limit of pure collective regime \(l = \langle v^2\tau _\textrm{N} \rangle \langle \tau _\textrm{U}^{-1}\rangle ^{-1}\) [250]. A more general expression for l that incorporates also resistive processes was eventually proposed in the context of a kinetic collective model, in which the thermal conductivity is expressed as the sum of a diffusive term (\(\kappa _K\)) and a collective term (\(\kappa _\textrm{C}\)) [252, 253].
Starting from the microscopic linearized BTE, Sendra et al. [254] derived an expression similar to Eq. (43) valid in the approximation of small but finite Knudsen number, and they provide expressions to compute the parameters \(\kappa \), l, and \(\alpha \) beyond the approximations of the kinetic collective model. For example, in these works, the nonlocal length for bulk silicon at room temperature was estimated to be \(l\sim 195\) nm. This model produces results in accordance with the truncated Lévy formalism with fractal dimension \(<2\) [255], which accounts for non-Fourier transport as observed in crystalline semiconductors and semiconducting alloys [253, 256, 257].
Using the relaxons formalism, Simoncelli et al. [258] derived two coupled general equations for the temperature and the drift velocity fields, valid for heat transport from the hydrodynamic to the diffusive regime. In these equations, a thermal viscosity coefficient (\(\mu \)) is added to the thermal conductivity (\(\kappa \)) as a materials parameter. While the details of this formalism are beyond the scope of this review, it is notable that this work introduced a parameter that allows one to assess the deviation from Fourier’s law due to phonon hydrodynamics. This “Fourier deviation number” (FDN) is expressed in terms of the dimensionless parameters of the newly derived viscous heat equations and correlates well with the \({\mathcal {L}}^2\) distance between the temperature profiles predicted by Fourier’s law and that obtained from the hydrodynamic equations. The analysis of FDN shows that Fourier transport can emerge even at nanometer-length-scales with important ballistic contributions when hydrodynamic effects are small compared to dissipative phonon scattering, thus reconciling the viscous transport formalism with the results in Refs. [231, 249]. It is indeed likely that the application of correct boundary conditions at the thermal bath provides a qualitative Fourier-like picture of heat transport at the nanoscale with length-dependent thermal conductivity, but hydrodynamic effects are responsible in the largest part for the non-Fourier behavior observed in the simulations and experiments on low-dimensional materials and nanoscale systems, including those reported in the previous sections.
The results of applying mesoscale hydrodynamic models to predict the thermal conductivity of nanostructures depend critically on the choice of the slip boundary conditions for the phonon flux at the surface, as for example in nanowires and thin films [251, 259, 260]. Atomistic MD or LD simulations can in some cases overcome this issue, as they provide a parameter-free understanding of how surfaces critically affect nanoscale heat transport, subject to the availability of reliable interatomic potentials. This has been the case for silicon-based materials, in particular nanowires and nano-membranes with rough, oxidized or nanostructured surfaces [261,262,263,264,265].
4.5 Thermal rectification
Besides phononic effects [141] thermal rectification may be attained by modulating electronic conduction, near-field radiation, excitonic effects in quantum structures, superconducting tunneling junctions, and reversible phase transition in phase change materials [266,267,268,269,270,271,272,273,274]. Here we review some of the works in which the original concept of the thermal diode, based on phonons non-linearity [135, 136], is investigated in realistic (nano)materials models by atomistic simulations.
Graphene-based thermal diodes: a trapezoidal patch (adapted with permission from [275]), b multilayer graphene step junction [276] (adapted with permission from [277], Copyright 2018, IOP), c defect-engineered nanoribbon [278] (adapted from [279], Copyright 2020, Elsevier), d nanoporous graphene, adapted with permission from [279], Copyright 2017, Wiley VCH. e Recalculated thermal rectification for small and large trapezoidal patches (LT, ST) and bilayer (BTM), trilayer (TTM), and quad-layer to monolayer (QTM) graphene step junctions [186]
The primary requirements for a phononic thermal diode are the asymmetry of the device with respect to the direction of the heat current and a strong temperature dependence of the phonon spectrum of the two sides of the device. To enable strong nonlinear effects, large temperature differences between the thermal reservoirs are necessary, which rule out any perturbative simulation method, e.g. EMD, BTE, or Landauer approaches. In fact, NEMD simulations have been extensively employed to calculate the rectification factor, \(f_r\) in Eq. (28), of several nanoscale systems and interfaces. Following the experimental demonstration of a thermal diode made of a mass-loaded CNT [143], carbon nanostructures have been proposed as potential thermal rectification devices. While NEMD simulations confirmed the relatively low rectification factors observed in experiments for mass-loaded CNTs (\(f_\textrm{R}<16\%\)) [217], spectacular \(f_\textrm{R}\) were predicted for triangular (120% and 250%) [280, 281], T-shaped, and trapezoidal (\(\sim 100\%\)) [275] graphene patches, multilayer graphene stacks (110%) [276], carbon nanocones (\(\gtrsim 100\%\)) [282], defect-engineered graphene nanoribbons (80% [278]), and branched nanoribbon junctions (470%) [283]. The highest \(f_\textrm{R}\), up to 2500%, have been reported for CNT-graphene junctions [284, 285], modifying a design originally proposed in Ref. [286]. The diode effect may be enhanced by designing interfaces in series, for example using nanoporous graphene phononic crystals, which lead to \(f_\textrm{R}\) up to 30% [279]. Large rectification factors were also predicted by NEMD simulations of asymmetric silicon-based nanostructures, such as telescopic silicon nanowires, graded silicon–germanium alloys, and porous silicon membranes [287,288,289].
Recent simulations, however, suggested that the rectification factor of nanoporous or defect-engineered graphene interfaces may be much lower (\(\sim 6\%\)) [290]. Also, a joint experimental and molecular simulation study showed that it is unlikely to obtain detectable thermal rectification in multilayer graphene step junctions [277]. Further examples of discrepancies among simulations of similar systems are reported in a recent comprehensive review of simulations and experiments on thermal rectification in 2D materials [291]. The reasons for such discrepancies lie in the details of the simulation setups. The calculation of \(f_r\) from NEMD is apparently straightforward, as it primarily consists of bookkeeping the heat flux, \(J_{+/-}\), in the forward and backward stationary heat transport conditions as determined by the temperature of the two thermal reservoirs. However, the choice of the thermostats and the size of the reservoirs may lead to substantial artifacts resulting in unphysical massive thermal rectification factors. For example, a configuration of a graphene patch with asymmetric thermal reservoirs in NEMD simulations and the Nosé–Hoover (NH) thermostat [292] gives an apparent rectification factor of 920% [293]. This is obviously an artifact of the simulation approach as the system is symmetric, thus violating the basic conditions to obtain a thermal diode. Hu et al. proved that Langevin dynamics provides thermally equilibrated heat baths with phonon distributions consistent with the classical canonical ensemble. Conversely, with global thermostats, such as the NH and NH-chain [292, 294] and velocity rescaling methods, provide a spatially uniform heat generation and nonequilibrium phonon populations in the thermal reservoirs [188]. Li et al. [186] recalculated the rectification factor for trapezoid graphene patches and multilayer step junctions, which were formerly predicted to have \(f_\textrm{R}\sim 100\%\) (Fig. 11a, b) [275, 276]. The revised NEMD simulations, in which thermal baths are equilibrated with the Langevin thermostat, give much more modest rectification factors, \(f_\textrm{R}<12\%\) (Fig. 11c). The analysis of the phonon density of states of the thermal baths shows that using the NH thermostat promotes artificially overpopulated modes, which presence depends on the bias conditions of the system and leads to unphysically large rectification effects. As most of the results reported above have been obtained using NH (chain) thermostats, they should be carefully ascertained using different thermalization methods or different parameters of the thermostats.
Interestingly, a systematic reverse-NEMD study of isotope-graded CNTs reported rectification efficiencies up to 40%, but with an opposite direction to that found in 1D graded chains: in these CNTs heat flows more efficiently from the low-mass to the high-mass end [295]. This surprising behavior is attributed to phonon scattering of longitudinal modes from perpendicular flexural modes, and it suggests that CNTs may not be used as real-world models to validate predictions for 1D systems.
5 Experiments
To conclude, we briefly mention some experimental investigations. The thermal properties of nanosized objects have an intrinsic technological interest in the field of nanoscale thermal management. In this general context, nanowires and single-walled nanotubes have been analyzed to look for deviation from the standard Fourier’s law. The typical setup to measure steady-state transport is the one sketched in Fig. 1 (see [296] for a more detailed description).
The first evidence of anomalous heat conduction in single-walled nanotubes was given in [297]. Further experimental evidence of anomalous transport in very long carbon nanotubes has been reported [298] although the results appear controversial [299]. The theoretical work suggesting the importance hydrodynamic effects in room temperature heat transport in graphene and 2D materials [196, 239, 260] fostered new experiments that lead to the observation of second sound in graphite [300]. The wave-like nature of heat conduction, which stands at the base of hydrodynamic effects, was also proven experimentally in phononic crystal nanostructures engendering phonon interference [301, 302]. Experiments demonstrating a non-trivial length dependence of thermal conductance for molecular chains have also been reported [303].
Another experiment displaying anomalous transport has been reported in [304]. The Authors give experimental evidence of the transition from 3D to 1D phonon transport in \(Nb Se_3\) nanowires of less than 26 nm in diameter. A superdiffusive thermal transport compatible with \(\kappa \sim L^{1/3}\), with a large enhancement of conductivity and a normal–superdiffusive transition is observed. These changes are attributed to strong stiffening along the direction of the molecular chain direction, which induces 1D along-chain phonons dominating thermal transport.
Other nanosystems where anomalous thermal transport is investigated are single-molecule junctions [305] and trapped linear ion chains [306]. It is conceivable that further experimental progress will occur even in this context in the next future.
6 Conclusion
Bridging theoretical models with experiments and technological applications is a challenging goal of physical sciences. This review aims at providing the reader with an updated overview of the many facets, originating from the discovery that anomalous heat transport characterizes low-dimensional models of matter. Many decades ago such a scenario could appear as a mere academic curiosity, due to the absence of possible experimental verifications. Nowadays, the exploration of states of matter at nanosize (polymers, nanotubes, carbon layers, etc.) has opened a realistic perspective for such investigations, together with many promising expectations of obtaining useful recipes for designing new materials and devices.
The first part of this manuscript illustrates how non-equilibrium statistical mechanics can provide a conceptual basis for predicting the basic mechanisms of non-Fourier transport in low-dimensional materials. Beyond details of the different models studied in the past for tackling this problem, the main message is that the hydrodynamic properties of heat transport in such systems, as expected, stem from basic conservation laws. This entails universal properties, that are typical of entire classes of models, thus indicating that the search for these anomalous transport effects should correspond to fully general features, irrespective of the adopted models of matter, sharing the same symmetries. Going through the reading of this first part one can appreciate the efforts to rationalize the overall theoretical matter in a consistent and convincing frame. In fact, the theoretical foundations of this problem presently rest on solid ground. In this respect, it is worth pointing out that not only predictions of asymptotic, i.e. thermodynamic-limit, properties, but also finite size effects can be suitably controlled. It can be easily realized that this is a crucial ingredient for a reliable comparison with experiments.
The importance of anomalous transport is further stressed by its influence on thermal management and conversion. As widely discussed in the second part of this review, this unveils unexpected possibilities for thermal rectification and for enhancing beyond standard bounds the efficiency of thermodynamic motors in nanosized materials, by exploiting also coupled transport processes. Relying on these achievements, one can reasonably forecast the possibility of exploring very important technological applications for effective work production from thermal processes and for new energy-saving opportunities.
The last part of this review is an overview of the various computational approaches worked out for investigating non-Fourier transport in realistic models of matter. This facet of the problem is of primary importance for checking “in silico” the signatures of anomalous transport when a direct experimental approach could be hardly effective. In fact, numerical simulations allow one to obtain reliable estimates of the finite-size effects (which typically are non-universal, i.e. model-dependent features) that may prevent the possibility of clear-cut experimental verification. One of the major problems is the possibility of having at disposal at least a numerical estimate of the mean-free path of thermal excitations. Only if the system under scrutiny is sensibly larger than this crucial parameter, one can reasonably expect to recover in a real sample of matter the predicted anomalous scaling properties of thermal conductivity with the system size. A short account of a few existing experimental results is eventually outlined. The recent progress and improvements in this direction could be considered as the prelude to a rapid growth of this research field, which certainly concerns basic aspects of physical sciences, but presumably could yield a major fallout for material science and its technological applications, far from being predictable just a few decades ago.
Finally, we point out that, while our review focused on anomalous thermal transport in classical systems, the quantum world opens up fascinating avenues. Anomalous transport in quantum mechanical systems is much less understood than in the classical case, for both practical and fundamental reasons. First of all, the computational complexity in the simulation of many-body quantum systems [307] grows exponentially with the number of particles, given the corresponding exponential growth of the size of the Hilbert space. On a more fundamental level, the same concept of local equilibrium should be carefully addressed in the quantum world. Indeed, we can have nanostructures smaller than the length scale over which electrons relax to a local equilibrium due to collisions with other electrons and phonons. As a consequence, effects due to quantum interference and entanglement should be taken into account in transport and energy conversion. Moreover, strong system-reservoir coupling and memory effects, which naturally feature in small quantum systems, make problematic the same definition of heat [308]. Notwithstanding the difficulties, a deeper understanding of energetics in the quantum regime, and the development of ideas and tools for efficient heat management is essential for the development of quantum technologies [309].
Data Availability
The datasets at disposal of the Authors used in this work are available from the corresponding author on reasonable request.
Notes
A chain of particles attached to on-site harmonic springs and interacting between themselves by collisions with nearby particles.
An alternative formulation of this statement, based on the well-known Wiener–Khintchine theorem and asymptotic analysis, is that the equilibrium power spectrum of the energy current has a zero-frequency singularity of the form \(\omega ^{-\gamma }\).
Equivalently, one can recast the results in reciprocal space. For instance, the dynamical structure factor \(S(k,\omega )\) of the particle displacement shows for \(k\rightarrow 0\) two sharp peaks at \(\omega = \pm ck\) that correspond to the propagation of sound modes and for \(\omega \approx \pm \omega _{\textrm{max}}\) it behaves as
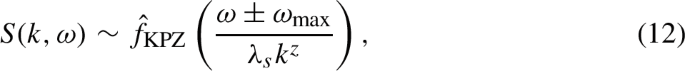
with \({\hat{f}}_{\textrm{KPZ}}\) being the transform of the scaling function.
References
S. Volz, J. Ordonez-Miranda, A. Shchepetov, M. Prunnila, J. Ahopelto, T. Pezeril, G. Vaudel, V. Gusev, P. Ruello, E.M. Weig et al., Nanophononics: state of the art and perspectives. Eur. Phys. J. B 89(1), 1–20 (2016)
S. Lepri, R. Livi, A. Politi, Thermal conduction in classical low-dimensional lattices. Phys. Rep. 377, 1 (2003). https://doi.org/10.1016/S0370-1573(02)00558-6
A. Dhar, Heat transport in low-dimensional systems. Adv. Phys. 57, 457–537 (2008). https://doi.org/10.1080/00018730802538522
A. Dhar, H. Spohn, Fourier’s law based on microscopic dynamics. Comptes Rendus Phys. 20(5), 393–401 (2019). https://doi.org/10.1016/j.crhy.2019.08.004
G. Benenti, S. Lepri, R. Livi, Anomalous heat transport in classical many-body systems: overview and perspectives. Front. Phys. 8, 292 (2020). https://doi.org/10.3389/fphy.2020.00292
A. Sellitto, V.A. Cimmelli, D. Jou, Mesoscopic Theories of Heat Transport in Nanosystems, vol. 6 (Springer, Heidelberg, 2016)
Y. Dong, Dynamical Analysis of non-Fourier Heat Conduction and Its Application in Nanosystems (Springer, New York, 2015)
V.A. Cimmelli, Different thermodynamic theories and different heat conduction laws. J. Non Equilib. Thermodyn. 34(4), 299–333 (2009)
G. Lebon, Heat conduction at micro and nanoscales: a review through the prism of extended irreversible thermodynamics. J. Non-Equilib. Thermodyn. 39(1), 35–59 (2014)
R. Kovács, P. Ván, Generalized heat conduction in heat pulse experiments. Int. J. Heat Mass Transf. 83, 613–620 (2015)
M. Wang, N. Yang, Z.-Y. Guo, Non-Fourier heat conductions in nanomaterials. J. Appl. Phys. 110(6), 064310 (2011)
G. Chen, Non-Fourier phonon heat conduction at the microscale and nanoscale. Nat. Rev. Phys. 3(8), 555–569 (2021)
Z. Zhang, Y. Ouyang, Y. Cheng, J. Chen, N. Li, G. Zhang, Size-dependent phononic thermal transport in low-dimensional nanomaterials. Phys. Rep. 860, 1–26 (2020)
A. Dhar, J.L. Lebowitz, Effect of phonon-phonon interactions on localization. Phys. Rev. Lett. 100(13), 134301 (2008). https://doi.org/10.1103/PhysRevLett.100.134301
K. Huang, Introduction to Statistical Physics (Chapman and Hall/CRC, London, 2009)
R. Peierls, R.E. Peierls, Quantum Theory of Solids (Oxford University Press, Oxford, 1955)
E. Fermi, J. Pasta, S. Ulam, Studies of nonlinear problems. Los Alamos Report LA-1940, 978 (1955)
F. Izrailev, A. Khisamutdinov, B. Chirikov, Numerical experiments with a chain of coupled anharmonic oscillators, Report 252 (Institute of Nuclear Physics, Novosibirsk, URSS, 1968). English translation: LA 4440
Z. Rieder, J.L. Lebowitz, E. Lieb, Properties of a harmonic crystal in a stationary nonequilibrium state. J. Math. Phys. 8, 1073 (1967)
A. Casher, J. Lebowitz, Heat flow in regular and disordered harmonic chains. J. Math. Phys. 12(8), 1701–1711 (1971)
A. O’Connor, J. Lebowitz, Heat-conduction and sound-transmission in isotopically disordered harmonic crystals. J. Math. Phys. 15(6), 692–703 (1974)
B. Alder, T. Wainwright, Velocity autocorrelations for hard spheres. Phys. Rev. Lett. 18(23), 988 (1967)
J. Dorfman, E. Cohen, Difficulties in the kinetic theory of dense gases. J. Math. Phys. 8(2), 282–297 (1967)
R. Livi, P. Politi, Nonequilibrium Statistical Physics: A Modern Perspective (Cambridge University Press, Cambridge, 2017)
Y. Pomeau, P. Résibois, Time dependent correlation functions and mode-mode coupling theories. Phys. Rep. 19(2), 63–139 (1975)
G. Casati, J. Ford, F. Vivaldi, W.M. Visscher, One-dimensional classical many-body system having a normal thermal conductivity. Phys. Rev. Lett. 52(21), 1861–1864 (1984)
S. Lepri (ed.), Thermal Transport in Low Dimensions: From Statistical Physics to Nanoscale Heat Transfer. Lecture Notes in Physics, vol. 921 (Springer, Berlin, 2016)
V. Zaburdaev, S. Denisov, J. Klafter, Lévy walks. Rev. Mod. Phys. 87(2), 483 (2015)
P. Cipriani, S. Denisov, A. Politi, From anomalous energy diffusion to Lévy walks and heat conductivity in one-dimensional systems. Phys. Rev. Lett. 94(24), 244301 (2005)
S. Lepri, A. Politi, Density profiles in open superdiffusive systems. Phys. Rev. E 83(3), 030107 (2011)
A. Dhar, K. Saito, B. Derrida, Exact solution of a Lévy walk model for anomalous heat transport. Phys. Rev. E 87, 010103 (2013)
S. Lepri, P. Sandri, A. Politi, The one-dimensional Lennard-Jones system: collective fluctuations and breakdown of hydrodynamics. Eur. Phys. J. B 47(4), 549–555 (2005)
S. Lepri, R. Livi, A. Politi, Heat transport in low dimensions: introduction and phenomenology. In: Lepri, S. (ed.) Thermal Transport in Low Dimensions; from Statistical Physics to Nanoscale Heat Transfer. Lecture Notes in Physics, vol. 921, pp. 1–37 (2016). https://doi.org/10.1007/978-3-319-29261-8_1
S. Lepri, R. Livi, A. Politi, Heat conduction in chains of nonlinear oscillators. Phys. Rev. Lett. 78(10), 1896–1899 (1997)
S. Lepri, R. Livi, A. Politi, On the anomalous thermal conductivity of one-dimensional lattices. Europhys. Lett. 43(3), 271–276 (1998)
S. Lepri, Memory effects and heat transport in one-dimensional insulators. Eur. Phys J. B 18(3), 441–446 (2000)
S. Denisov, J. Klafter, M. Urbakh, Dynamical heat channels. Phys. Rev. Lett. 91(19), 194301 (2003)
A. Kundu, C. Bernardin, K. Saito, A. Kundu, A. Dhar, Fractional equation description of an open anomalous heat conduction set-up. J. Stat. Mech. Theory Exp. 2019(1), 013205 (2019)
A. Dhar, A. Kundu, A. Kundu, Anomalous heat transport in one dimensional systems: a description using non-local fractional-type diffusion equation. Front. Phys. 7, 159 (2019)
A. Lippi, R. Livi, Heat conduction in two-dimensional nonlinear lattices. J. Stat. Phys. 100(5–6), 1147–1172 (2000)
L. Wang, B. Hu, B. Li, Logarithmic divergent thermal conductivity in two-dimensional nonlinear lattices. Phys. Rev. E 86, 040101 (2012)
P. Di Cintio, R. Livi, S. Lepri, G. Ciraolo, Multiparticle collision simulations of two-dimensional one-component plasmas: anomalous transport and dimensional crossovers. Phys. Rev. E 95, 043203 (2017). https://doi.org/10.1103/PhysRevE.95.043203
K. Saito, A. Dhar, Heat conduction in a three dimensional anharmonic crystal. Phys. Rev. Lett. 104, 040601 (2010)
L. Wang, D. He, B. Hu, Heat conduction in a three-dimensional momentum-conserving anharmonic lattice. Phys. Rev. Lett. 105, 160601 (2010). https://doi.org/10.1103/PhysRevLett.105.160601
K. Aoki, D. Kusnezov, Bulk properties of anharmonic chains in strong thermal gradients: non-equilibrium \(\phi ^4\) theory. Phys. Lett. A 265(4), 250 (2000)
B. Hu, B. Li, H. Zhao, Heat conduction in one-dimensional chains. Phys. Rev. E 57(3), 2992 (1998)
C. Giardiná, R. Livi, A. Politi, M. Vassalli, Finite thermal conductivity in 1d lattices. Phys. Rev. Lett. 84(10), 2144–2147 (2000)
O.V. Gendelman, A.V. Savin, Normal heat conductivity of the one-dimensional lattice with periodic potential of nearest-neighbor interaction. Phys. Rev. Lett. 84(11), 2381–2384 (2000)
A. Iacobucci, F. Legoll, S. Olla, G. Stoltz, Negative thermal conductivity of chains of rotors with mechanical forcing. Phys. Rev. E 84(6), 061108 (2011)
S. Iubini, S. Lepri, R. Livi, A. Politi, Coupled transport in rotor models. New J. Phys. 18(8), 083023 (2016)
H. Spohn, Fluctuating hydrodynamics for a chain of nonlinearly coupled rotators. arXiv preprint arXiv:1411.3907 (2014)
P.G. Kevrekidis, The Discrete Nonlinear Schrödinger Equation: Mathematical Analysis, Numerical Computations and Physical Perspectives, vol. 232 (Springer, Berlin, 2009)
S. Iubini, S. Lepri, A. Politi, Nonequilibrium discrete nonlinear Schrödinger equation. Phys. Rev. E 86, 011108 (2012). https://doi.org/10.1103/PhysRevE.86.011108
S. Iubini, S. Lepri, R. Livi, A. Politi, Off-equilibrium Langevin dynamics of the discrete nonlinear Schroedinger chain. J. Stat. Mech: Theory Exp. 08, 08017 (2013)
C.B. Mendl, H. Spohn, Low temperature dynamics of the one-dimensional discrete nonlinear Schroedinger equation. J. Stat. Mech. Theory Exp. 2015(8), 08028 (2015). https://doi.org/10.1088/1742-5468/2015/08/P08028
S. Iubini, S. Lepri, R. Livi, G.-L. Oppo, A. Politi, A chain, a bath, a sink, and a wall. Entropy 19(9), 445 (2017)
C.Y. Gao, D.T. Limmer, Nonlinear transport coefficients from large deviation functions. J. Chem. Phys. 151(1), 014101 (2019)
U. Ray, D.T. Limmer, Heat current fluctuations and anomalous transport in low-dimensional carbon lattices. Phys. Rev. B 100(24), 241409 (2019)
A.-L. Barabási, H.E. Stanley et al., Fractal Concepts in Surface Growth (Cambridge University Press, Cambridge, 1995)
H. Spohn, Nonlinear fluctuating hydrodynamics for anharmonic chains. J. Stat. Phys. 154(5), 1191–1227 (2014)
H. van Beijeren, Exact results for anomalous transport in one-dimensional Hamiltonian systems. Phys. Rev. Lett. 108, 180601 (2012)
H. Spohn, Fluctuating hydrodynamics approach to equilibrium time correlations for anharmonic chains, in Thermal Transport in Low Dimensions (Springer, Berlin, 2016), pp.107–158
R. Klages, G. Radons, I.M. Sokolov (eds.), Anomalous Transport: Foundations and Applications (Wiley-VCH Verlag, Weinheim, 2008)
C.B. Mendl, H. Spohn, Dynamic correlators of Fermi-Pasta-Ulam chains and nonlinear fluctuating hydrodynamics. Phys. Rev. Lett. 111, 230601 (2013)
S. Das, A. Dhar, O. Narayan, Heat conduction in the \(\alpha \)-\(\beta \) Fermi-Pasta-Ulam chain. J. Stat. Phys. 154(1–2), 204–213 (2014)
C.B. Mendl, H. Spohn, Equilibrium time-correlation functions for one-dimensional hard-point systems. Phys. Rev. E 90(1), 012147 (2014)
S.G. Das, A. Dhar, K. Saito, C.B. Mendl, H. Spohn, Numerical test of hydrodynamic fluctuation theory in the Fermi-Pasta-Ulam chain. Phys. Rev. E 90(1), 012124 (2014)
P. Di Cintio, R. Livi, H. Bufferand, G. Ciraolo, S. Lepri, M.J. Straka, Anomalous dynamical scaling in anharmonic chains and plasma models with multiparticle collisions. Phys. Rev. E 92, 062108 (2015)
R. Barreto, M. Carusela, A. Monastra, Nonlinear fluctuating hydrodynamics with many conserved fields: the case of a three-dimensional anharmonic chain. Phys. Rev. E 100(2), 022118 (2019)
P.I. Hurtado, P.L. Garrido, A violation of universality in anomalous Fourier’s law. Sci. Rep. 6, 38823 (2016)
M. Kulkarni, D.A. Huse, H. Spohn, Fluctuating hydrodynamics for a discrete Gross-Pitaevskii equation: mapping onto the Kardar-Parisi-Zhang universality class. Phys. Rev. A 92(4), 043612 (2015)
S. Lepri, R. Livi, A. Politi, Too close to integrable: crossover from normal to anomalous heat diffusion. Phys. Rev. Lett. 125(4), 040604 (2020)
S. Lepri, R. Livi, A. Politi, Universality of anomalous one-dimensional heat conductivity. Phys. Rev. E 68(6, Part 2), 067102 (2003). https://doi.org/10.1103/PhysRevE.68.067102
G. Lee-Dadswell, Universality classes for thermal transport in one-dimensional oscillator systems. Phys. Rev. E 91(3), 032102 (2015)
G. Basile, C. Bernardin, S. Olla, Momentum conserving model with anomalous thermal conductivity in low dimensional systems. Phys. Rev. Lett. 96, 204303 (2006)
S. Lepri, C. Mejía-Monasterio, A. Politi, Stochastic model of anomalous heat transport. J. Phys. A Math. Theor. 42, 025001 (2009)
G. Basile, L. Delfini, S. Lepri, R. Livi, S. Olla, A. Politi, Anomalous transport and relaxation in classical one-dimensional models. Eur. Phys. J. Spec. Top. 151, 85–93 (2007)
A. Iacobucci, F. Legoll, S. Olla, G. Stoltz, Thermal conductivity of the Toda lattice with conservative noise. J. Stat. Phys. 140(2), 336–348 (2010). https://doi.org/10.1007/s10955-010-9996-6
A. Pereverzev, Fermi-Pasta-Ulam \(\beta {}\) lattice: Peierls equation and anomalous heat conductivity. Phys. Rev. E 68(5), 056124 (2003). https://doi.org/10.1103/PhysRevE.68.056124
B. Nickel, The solution to the 4-phonon Boltzmann equation for a 1d chain in a thermal gradient. J. Phys. A Math. Gen. 40(6), 1219–1238 (2007). https://doi.org/10.1088/1751-8113/40/6/003
J. Lukkarinen, H. Spohn, Anomalous energy transport in the FPU-\(\beta \) chain. Commun. Pure Appl. Math. 61(12), 1753–1786 (2008). https://doi.org/10.1002/cpa.20243
G. Dematteis, L. Rondoni, D. Proment, F. De Vita, M. Onorato, Coexistence of ballistic and Fourier regimes in the \(\beta \) Fermi-Pasta-Ulam-Tsingou lattice. Phys. Rev. Lett. 125(2), 024101 (2020)
L. Wang, T. Wang, Power-law divergent heat conductivity in one-dimensional momentum-conserving nonlinear lattices. EPL (Europhys. Lett.) 93, 54002 (2011)
V. Popkov, A. Schadschneider, J. Schmidt, G.M. Schütz, Fibonacci family of dynamical universality classes. Proc. Natl. Acad. Sci. 112(41), 12645–12650 (2015)
S. Tamaki, M. Sasada, K. Saito, Heat transport via low-dimensional systems with broken time-reversal symmetry. Phys. Rev. Lett. 119(11), 110602 (2017)
K. Saito, M. Sasada, Thermal conductivity for coupled charged harmonic oscillators with noise in a magnetic field. Commun. Math. Phys. 361(3), 951–995 (2018)
M. Toda, Solitons and heat-conduction. Phys. Scr. 20(3–4), 424–430 (1979)
X. Zotos, Ballistic transport in classical and quantum integrable systems. J. Low Temp. Phys. 126(3–4), 1185–1194 (2002)
B.S. Shastry, A. Young, Dynamics of energy transport in a Toda ring. Phys. Rev. B 82(10), 104306 (2010)
P. Mazur, Non-ergodicity of phase functions in certain systems. Physica 43(4), 533–545 (1969)
H. Spohn, Interacting and noninteracting integrable systems. J. Math. Phys. 59(9), 091402 (2018). https://doi.org/10.1063/1.5018624
N. Theodorakopoulos, M. Peyrard, Solitons and nondissipative diffusion. Phys. Rev. Lett. 83(12), 2293 (1999)
A. Kundu, A. Dhar, Equilibrium dynamical correlations in the Toda chain and other integrable models. Phys. Rev. E 94, 062130 (2016). https://doi.org/10.1103/PhysRevE.94.062130
P. Di Cintio, S. Iubini, S. Lepri, R. Livi, Transport in perturbed classical integrable systems: the pinned Toda chain. Chaos Solitons Fractals 117, 249–254 (2018)
A. Das, M. Kulkarni, H. Spohn, A. Dhar, Kardar-Parisi-Zhang scaling for an integrable lattice Landau-Lifshitz spin chain. Phys. Rev. E 100(4), 042116 (2019)
S. Chen, J. Wang, G. Casati, G. Benenti, Nonintegrability and the Fourier heat conduction law. Phys. Rev. E 90, 032134 (2014). https://doi.org/10.1103/PhysRevE.90.032134
L. Pitaevskii, E. Lifshitz, Physical Kinetics: Volume 10 of Course of Theoretical Physics (Butterworth-Heinemann, Burlington, 2012)
K. Aoki, D. Kusnezov, Fermi-Pasta-Ulam \(\beta \) model: boundary jumps, Fourier’s law, and scaling. Phys. Rev. Lett. 86(18), 4029–4032 (2001)
S. Lepri, R. Livi, A. Politi, Studies of thermal conductivity in Fermi-Pasta-Ulam-like lattices. Chaos 15(1), 015118 (2005). https://doi.org/10.1063/1.1854281
L. Delfini, S. Lepri, R. Livi, C. Mejia-Monasterio, A. Politi, Nonequilibrium dynamics of a stochastic model of anomalous heat transport: numerical analysis. J. Phys. A Math. Theor. 43(14), 145001 (2010)
Y. Zhong, Y. Zhang, J. Wang, H. Zhao, Normal heat conduction in one-dimensional momentum conserving lattices with asymmetric interactions. Phys. Rev. E 85, 060102 (2012)
L. Wang, B. Hu, B. Li, Validity of Fourier’s law in one-dimensional momentum-conserving lattices with asymmetric interparticle interactions. Phys. Rev. E 88, 052112 (2013)
G.R. Lee-Dadswell, Predicting and identifying finite-size effects in current spectra of one-dimensional oscillator chains. Phys. Rev. E 91, 012138 (2015)
A. Miron, J. Cividini, A. Kundu, D. Mukamel, Derivation of fluctuating hydrodynamics and crossover from diffusive to anomalous transport in a hard-particle gas. Phys. Rev. E 99(1), 012124 (2019)
A. Campa, T. Dauxois, S. Ruffo, Statistical mechanics and dynamics of solvable models with long-range interactions. Phys. Rep. 480(3), 57–159 (2009)
A. Campa, T. Dauxois, D. Fanelli, S. Ruffo, Physics of Long-range Interacting Systems (OUP Oxford, Oxford, 2014)
F.J. Dyson, Existence of a phase-transition in a one-dimensional Ising ferromagnet. Commun. Math. Phys. 12(2), 91–107 (1969)
N. Defenu, T. Donner, T. Macrì, G. Pagano, S. Ruffo, A. Trombettoni, Long-range interacting quantum systems (2021). arXiv:2109.01063 [cond-mat.quant-gas]
A. Torcini, S. Lepri, Disturbance propagation in chaotic extended systems with long-range coupling. Phys. Rev. E 55(4), 3805 (1997)
D. Métivier, R. Bachelard, M. Kastner, Spreading of perturbations in long-range interacting classical lattice models. Phys. Rev. Lett. 112(21), 210601 (2014)
F. Bouchet, S. Gupta, D. Mukamel, Thermodynamics and dynamics of systems with long-range interactions. Phys. A Stat. Mech. Appl. 389(20), 4389–4405 (2010)
P. de Buyl, G. De Ninno, D. Fanelli, C. Nardini, A. Patelli, F. Piazza, Y.Y. Yamaguchi, Absence of thermalization for systems with long-range interactions coupled to a thermal bath. Phys. Rev. E 87, 042110 (2013)
S. Iubini, S. Lepri, S. Ruffo, Hydrodynamics and transport in the long-range-interacting \(\varphi ^{4}\) chain. J. Stat. Mech. 3, 033209 (2022)
R.C. Desai, R. Zwanzig, Statistical mechanics of a nonlinear stochastic model. J. Stat. Phys. 19(1), 1–24 (1978)
T. Dauxois, S. Lepri, S. Ruffo, Clustering and ensembles inequivalence in the \(\varphi ^4\) and \(\varphi ^6\) mean-field Hamiltonian models. Commun. Nonlinear Sci. Numer. Simul. 8(3–4), 375–387 (2003)
D. Bagchi, Thermal transport in the Fermi-Pasta-Ulam model with long-range interactions. Phys. Rev. E 95(3), 032102 (2017)
D. Bagchi, Heat transport in long-ranged Fermi-Pasta-Ulam-Tsingou-type models. Phys. Rev. E 104(5), 054108 (2021)
C. Olivares, C. Anteneodo, Role of the range of the interactions in thermal conduction. Phys. Rev. E 94, 042117 (2016)
S. Iubini, P. Di Cintio, S. Lepri, R. Livi, L. Casetti, Heat transport in oscillator chains with long-range interactions coupled to thermal reservoirs. Phys. Rev. E 97, 032102 (2018). https://doi.org/10.1103/PhysRevE.97.032102
G. Miloshevich, J.-P. Nguenang, T. Dauxois, R. Khomeriki, S. Ruffo, Instabilities and relaxation to equilibrium in long-range oscillator chains. Phys. Rev. E 91(3), 032927 (2015)
G.N.B. Chendjou, J.P. Nguenang, A. Trombettoni, T. Dauxois, R. Khomeriki, S. Ruffo, Fermi-Pasta-Ulam chains with harmonic and anharmonic long-range interactions. Commun. Nonlinear Sci. Numer. Simul. 60, 115–127 (2018). https://doi.org/10.1016/j.cnsns.2018.01.006
V.E. Tarasov, Continuous limit of discrete systems with long-range interaction. J. Phys. A Math. Gen. 39(48), 14895 (2006)
N. Defenu, Metastability and discrete spectrum of long-range systems. Proc. Natl. Acad. Sci. 118(30), e2101785118 (2021)
R. Metzler, J. Klafter, The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339(1), 1–77 (2000)
P. Di Cintio, S. Iubini, S. Lepri, R. Livi, Equilibrium time-correlation functions of the long-range interacting Fermi-Pasta-Ulam model. J. Phys. A Math. Theor. 52(27), 274001 (2019). https://doi.org/10.1088/1751-8121/ab22f7
S. Tamaki, K. Saito, Energy current correlation in solvable long-range interacting systems. Phys. Rev. E 101(4), 042118 (2020)
H. Suda, A family of fractional diffusion equations derived from stochastic harmonic chains with long-range interactions, in Annales de l’Institut Henri Poincaré, Probabilités et Statistiques, vol. 57 (Institut Henri Poincaré, 2021), pp. 2268–2314
A. Malevanets, R. Kapral, Mesoscopic model for solvent dynamics. J. Chem. Phys. 110, 8605 (1999)
G. Benenti, G. Casati, C. Mejía-Monasterio, Thermoelectric efficiency in momentum-conserving systems. N. J. Phys. 16(1), 015014 (2014). https://doi.org/10.1088/1367-2630/16/1/015014
S. Lepri, G. Ciraolo, P. Di Cintio, J. Gunn, R. Livi, Kinetic and hydrodynamic regimes in multi-particle-collision dynamics of a one-dimensional fluid with thermal walls. Phys. Rev. Res. 3(1), 013207 (2021)
O. Narayan, S. Ramaswamy, Anomalous heat conduction in one-dimensional momentum-conserving systems. Phys. Rev. Lett. 89(20), 200601 (2002)
H. Zhao, W.G. Wang, Fourier heat conduction as a strong kinetic effect in one-dimensional hard-core gases. Phys. Rev. E 97, 010103 (2018)
R. Luo, L. Huang, S. Lepri, Heat conduction in a three-dimensional momentum-conserving fluid. Phys. Rev. E 103(5), 050102 (2021)
R. Samanta, I.V. Protopopov, A.D. Mirlin, D.B. Gutman, Thermal transport in one-dimensional electronic fluids. Phys. Rev. Lett. 122, 206801 (2019). https://doi.org/10.1103/PhysRevLett.122.206801
M. Terraneo, M. Peyrard, G. Casati, Controlling the energy flow in nonlinear lattices: a model for a thermal rectifier. Phys. Rev. Lett. 88, 094302 (2002). https://doi.org/10.1103/PhysRevLett.88.094302
B. Li, L. Wang, G. Casati, Thermal diode: rectification of heat flux. Phys. Rev. Lett. 93(18), 184301 (2004). https://doi.org/10.1103/PhysRevLett.93.184301
M. Peyrard, The design of a thermal rectifier. EPL 76, 49 (2006). https://doi.org/10.1209/epl/i2006-10223-5
B. Li, L. Wang, G. Casati, Negative differential thermal resistance and thermal transistor. Appl. Phys. Lett. 88, 143501 (2006). https://doi.org/10.1063/1.2191730
B. Hu, L. Yang, Y. Zhang, Asymmetric heat conduction in nonlinear lattices. Phys. Rev. Lett. 97, 124392 (2006). https://doi.org/10.1103/PhysRevLett.97.124302
N. Yang, N. Li, L. Wang, B. Li, Thermal rectification and negative differential thermal resistance in lattices with mass gradient. Phys. Rev. B 76, 02001 (2007). https://doi.org/10.1103/PhysRevB.76.020301
N. Li, J. Ren, L. Wang, G. Zhang, P. Hänggi, B. Li, Colloquium: phononics: manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 84, 1045–1066 (2012). https://doi.org/10.1103/RevModPhys.84.1045
G. Benenti, G. Casati, C. Mejía-Monasterio, M. Peyrard, From thermal rectifiers to thermoelectric devices, chap. 10, in Thermal Transport in Low Dimensions: From Statistical Physics to Nanoscale Heat Transfer. ed. by S. Lepri (Springer, Cham, 2016), pp.365–407. https://doi.org/10.1007/978-3-319-29261-8_10
C.W. Chang, D. Okawa, A. Majumdar, A. Zettl, Solid-state thermal rectifier. Science 314(5802), 1121–1124 (2006). https://doi.org/10.1126/science.1132898
W. Kobayashi, T. Teraoka, I. Terasaki, An oxide thermal rectifier. Appl. Phys. Lett. 95, 171905 (2009). https://doi.org/10.1063/1.3253712
D. Sawaki, W. Kobayashi, Y. Morimoto, I. Terasaki, Thermal rectification in bulk materials with asymmetric shape. Appl. Phys. Lett. 98, 081915 (2011). https://doi.org/10.1063/1.3559615
W. Kobayashi, D. Sawaki, T. Omura, T. Katsufuji, Y. Moritomo, I. Terasaki, Thermal rectification in the vicinity of a structural phase transition. Appl. Phys. Express 5, 027302 (2012). https://doi.org/10.1143/apex.5.027302
M. Schmotz, J. Maier, E. Scheer, P. Leiderer, A thermal diode using phonon rectification. N. J. Phys. 13(11), 113027 (2011). https://doi.org/10.1088/1367-2630/13/11/113027
N.A. Roberts, D.G. Walker, A review of thermal rectification observations and models in solid materials. Int. J. Therm. Sci. 50(5), 648–662 (2011). https://doi.org/10.1016/j.ijthermalsci.2010.12.004
H. Tian, D. Xie, Y. Yang, T.-L. Ren, G. Zhang, Y.-F. Wang, C.-J. Zhou, P.-G. Peng, L.-G. Wang, L.-T. Liu, A novel solid-state thermal rectifier based on reduced graphene oxide. Sci. Rep. 2, 523 (2012). https://doi.org/10.1038/srep00523
H. Wang, S. Hu, K. Takahashi, X. Zhang, H. Takamatsu, J. Chen, Experimental study of thermal rectification in suspended monolayer graphene. Nat. Commun. 8(1), 15843 (2017). https://doi.org/10.1038/ncomms15843
F. Liu, M. Muruganathan, Y. Feng, S. Ogawa, Y. Morita, C. Liu, J. Guo, M. Schmidt, H. Mizuta, Thermal rectification on asymmetric suspended graphene nanomesh devices. Nano Futures 5(4), 045002 (2021). https://doi.org/10.1088/2399-1984/ac36b5
S. Chen, D. Donadio, G. Benenti, G. Casati, Efficient thermal diode with ballistic spacer. Phys. Rev. E 97, 030101 (2018). https://doi.org/10.1103/PhysRevE.97.030101
A. Shakouri, Recent developments in semiconductor thermoelectric physics and materials. Annu. Rev. Mater. Res. 41(1), 399–431 (2011). https://doi.org/10.1146/annurev-matsci-062910-100445
Y. Dubi, M. Di Ventra, Colloquium: heat flow and thermoelectricity in atomic and molecular junctions. Rev. Mod. Phys. 83, 131–155 (2011). https://doi.org/10.1103/RevModPhys.83.131
G. Benenti, G. Casati, K. Saito, R.S. Whitney, Fundamental aspects of steady-state conversion of heat to work at the nanoscale. Phys. Rep. 694, 1–124 (2017). https://doi.org/10.1016/j.physrep.2017.05.008
D. Narducci, J.G. Snyder, C.E. Fanciulli, Advances in Thermoelectricity: Foundational Issues, Materials and Nanotechnology (IOS Press, Amsterdam, 2021)
H.B. Callen, Thermodynamics and an Introduction to Thermostatics (Wiley, New York, 1985)
S.R. de Groot, P. Mazur, Non-Equilibrium Thermodynamics (Dover, New York, 1984)
G. Benenti, G. Casati, J. Wang, Conservation laws and thermodynamic efficiencies. Phys. Rev. Lett. 110, 070604 (2013). https://doi.org/10.1103/PhysRevLett.110.070604
S. Chen, J. Wang, G. Casati, G. Benenti, Thermoelectricity of interacting particles: a numerical approach. Phys. Rev. E 92, 032139 (2015). https://doi.org/10.1103/PhysRevE.92.032139
U. Seifert, From stochastic thermodynamics to thermodynamic inference. Annu. Rev. Condens. Matter Phys. 10(1), 171–192 (2019). https://doi.org/10.1146/annurev-conmatphys-031218-013554
J.M. Horowitz, T.R. Gingrich, Thermodynamic uncertainty relations constrain non-equilibrium fluctuations. Nat. Phys. 16(1), 15–20 (2020). https://doi.org/10.1038/s41567-019-0702-6
P. Pietzonka, U. Seifert, Universal trade-off between power, efficiency, and constancy in steady-state heat engines. Phys. Rev. Lett. 120, 190602 (2018). https://doi.org/10.1103/PhysRevLett.120.190602
G. Benenti, G. Casati, J. Wang, Power, efficiency, and fluctuations in steady-state heat engines. Phys. Rev. E 102, 040103 (2020). https://doi.org/10.1103/PhysRevE.102.040103
B. Cleuren, C. Van den Broeck, Random walks with absolute negative mobility. Phys. Rev. E 65, 030101 (2002). https://doi.org/10.1103/PhysRevE.65.030101
R. Eichhorn, P. Reimann, P. Hänggi, Brownian motion exhibiting absolute negative mobility. Phys. Rev. Lett. 88, 190601 (2002). https://doi.org/10.1103/PhysRevLett.88.190601
D. Reguera, A. Luque, P.S. Burada, G. Schmid, J.M. Rubí, P. Hänggi, Entropic splitter for particle separation. Phys. Rev. Lett. 108, 020604 (2012). https://doi.org/10.1103/PhysRevLett.108.020604
A. Słapik, J. Łuczka, P. Hänggi, J. Spiechowicz, Tunable mass separation via negative mobility. Phys. Rev. Lett. 122, 070602 (2019). https://doi.org/10.1103/PhysRevLett.122.070602
P.K. Ghosh, P. Hänggi, F. Marchesoni, F. Nori, Giant negative mobility of janus particles in a corrugated channel. Phys. Rev. E 89, 062115 (2014). https://doi.org/10.1103/PhysRevE.89.062115
A. Sarracino, F. Cecconi, A. Puglisi, A. Vulpiani, Nonlinear response of inertial tracers in steady laminar flows: differential and absolute negative mobility. Phys. Rev. Lett. 117, 174501 (2016). https://doi.org/10.1103/PhysRevLett.117.174501
B.J. Keay, S. Zeuner, S.J. Allen, K.D. Maranowski, A.C. Gossard, U. Bhattacharya, M.J.W. Rodwell, Dynamic localization, absolute negative conductance, and stimulated, multiphoton emission in sequential resonant tunneling semiconductor superlattices. Phys. Rev. Lett. 75, 4102–4105 (1995). https://doi.org/10.1103/PhysRevLett.75.4102
A. Ros, R. Eichhorn, J. Regtmeier, T.T. Duong, P. Reimann, D. Anselmetti, Absolute negative particle mobility. Nature 436(7053), 928–928 (2005). https://doi.org/10.1038/436928a
J. Nagel, D. Speer, T. Gaber, A. Sterck, R. Eichhorn, P. Reimann, K. Ilin, M. Siegel, D. Koelle, R. Kleiner, Observation of negative absolute resistance in a Josephson junction. Phys. Rev. Lett. 100, 217001 (2008). https://doi.org/10.1103/PhysRevLett.100.217001
J. Cividini, D. Mukamel, H.A. Posch, Driven tracer with absolute negative mobility. J. Phys. A Math. Theor. 51(8), 085001 (2018). https://doi.org/10.1088/1751-8121/aaa630
J. Wang, G. Casati, G. Benenti, Inverse currents in Hamiltonian coupled transport. Phys. Rev. Lett. 124, 110607 (2020). https://doi.org/10.1103/PhysRevLett.124.110607
G. Benenti, G. Casati, F. Marchesoni, J. Wang, Autonomous circular heat engine. Phys. Rev. E 106, 044104 (2022). https://doi.org/10.1103/PhysRevE.106.044104
E.H. Lieb, W. Liniger, Exact analysis of an interacting Bose gas. I. The general solution and the ground state. Phys. Rev. 130, 1605–1616 (1963). https://doi.org/10.1103/PhysRev.130.1605
E.H. Lieb, Exact analysis of an interacting Bose gas. II. The excitation spectrum. Phys. Rev. 130, 1616–1624 (1963). https://doi.org/10.1103/PhysRev.130.1616
A. Garriga, J. Kurchan, F. Ritort, Strong Soret effect in one dimension. J. Stat. Phys. 106(1), 109–123 (2002). https://doi.org/10.1023/A:1013182909209
J. Wang, G. Casati, One-dimensional self-organization and nonequilibrium phase transition in a Hamiltonian system. Phys. Rev. Lett. 118, 040601 (2017). https://doi.org/10.1103/PhysRevLett.118.040601
M. Horvat, T. Prosen, G. Casati, Exactly solvable model of a highly efficient thermoelectric engine. Phys. Rev. E 80(1), 010102 (2009)
J. Wang, G. Casati, Tcv Prosen, C.-H. Lai, One-dimensional hard-point gas as a thermoelectric engine. Phys. Rev. E 80, 031136 (2009). https://doi.org/10.1103/PhysRevE.80.031136
D. Donadio, Simulation of dimensionality effects in thermal transport, in Thermal Transport in Low Dimensions. Lecture Notes in Physics, vol. 921, ed. by S. Lepri (Springer, Cham, 2016), pp.275–304. https://doi.org/10.1007/978-3-319-29261-8_7
F. Müller-Plathe, A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 106(14), 6082–6085 (1997). https://doi.org/10.1063/1.473271
S. Kuang, J.D. Gezelter, A gentler approach to RNEMD: nonisotropic velocity scaling for computing thermal conductivity and shear viscosity. J. Chem. Phys. 133(16), 164101 (2010). https://doi.org/10.1063/1.3499947
Z. Li, S. Xiong, C. Sievers, Y. Hu, Z. Fan, N. Wei, H. Bao, S. Chen, D. Donadio, T. Ala-Nissila, Influence of thermostatting on nonequilibrium molecular dynamics simulations of heat conduction in solids. J. Chem. Phys. 151(23), 234105 (2019). https://doi.org/10.1063/1.5132543
D.P. Sellan, E.S. Landry, J.E. Turney, A.J.H. McGaughey, C.H. Amon, Size effects in molecular dynamics thermal conductivity predictions. Phys. Rev. B 81(21), 214305 (2010). https://doi.org/10.1103/PhysRevB.81.214305
Y. Hu, T. Feng, X. Gu, Z. Fan, X. Wang, M. Lundstrom, S.S. Shrestha, H. Bao, Unification of nonequilibrium molecular dynamics and the mode-resolved phonon Boltzmann equation for thermal transport simulations. Phys. Rev. B 101(15), 155308 (2020). https://doi.org/10.1103/PhysRevB.101.155308
E. Lampin, P.L. Palla, P.-A. Francioso, F. Cleri, Thermal conductivity from approach-to-equilibrium molecular dynamics. J. Appl. Phys. 114(3), 033525 (2013). https://doi.org/10.1063/1.4815945
Z. Fan, H. Dong, A. Harju, T. Ala-Nissila, Homogeneous nonequilibrium molecular dynamics method for heat transport and spectral decomposition with many-body potentials. Phys. Rev. B 99(6), 064308 (2019). https://doi.org/10.1103/PhysRevB.99.064308
M. Omini, A. Sparavigna, Beyond the isotropic-model approximation in the theory of thermal conductivity. Phys. Rev. B 53(14), 9064–9073 (1996). https://doi.org/10.1103/PhysRevB.53.9064
A. Cepellotti, N. Marzari, Thermal transport in crystals as a kinetic theory of relaxons. Phys. Rev. X 6(4), 041013 (2016). https://doi.org/10.1103/PhysRevX.6.041013
T. Feng, X. Ruan, Quantum mechanical prediction of four-phonon scattering rates and reduced thermal conductivity of solids. Phys. Rev. B 93(4), 045202 (2016). https://doi.org/10.1103/PhysRevB.93.045202
T. Feng, L. Lindsay, X. Ruan, Four-phonon scattering significantly reduces intrinsic thermal conductivity of solids. Phys. Rev. B 96(16), 161201 (2017). https://doi.org/10.1103/PhysRevB.96.161201
G. Barbalinardo, Z. Chen, N.W. Lundgren, D. Donadio, Efficient anharmonic lattice dynamics calculations of thermal transport in crystalline and disordered solids. J. Appl. Phys. 128(13), 135104 (2020). https://doi.org/10.1063/5.0020443
A. Cepellotti, G. Fugallo, L. Paulatto, M. Lazzeri, F. Mauri, N. Marzari, Phonon hydrodynamics in two-dimensional materials. Nat. Commun. 6(1), 6400 (2015). https://doi.org/10.1038/ncomms7400
J.E. Turney, E.S. Landry, A.J.H. McGaughey, C.H. Amon, Predicting phonon properties and thermal conductivity from anharmonic lattice dynamics calculations and molecular dynamics simulations. Phys. Rev. B 79(6), 064301 (2009). https://doi.org/10.1103/PhysRevB.79.064301
A. Henry, G. Chen, High thermal conductivity of single polyethylene chains using molecular dynamics simulations. Phys. Rev. Lett. 101(23), 235502 (2008). https://doi.org/10.1103/PhysRevLett.101.235502
J. Liu, R. Yang, Length-dependent thermal conductivity of single extended polymer chains. Phys. Rev. B 86(10), 104307 (2012). https://doi.org/10.1103/PhysRevB.86.104307
A. Crnjar, C. Melis, L. Colombo, Assessing the anomalous superdiffusive heat transport in a single one-dimensional PEDOT chain. Phys. Rev. Mater. 2(1), 015603 (2018). https://doi.org/10.1103/PhysRevMaterials.2.015603
J.J. Freeman, G.J. Morgan, C.A. Cullen, Thermal conductivity of a single polymer chain. Phys. Rev. B 35, 7627–7635 (1987). https://doi.org/10.1103/PhysRevB.35.7627
A. Henry, G. Chen, S.J. Plimpton, A. Thompson, 1d-to-3d transition of phonon heat conduction in polyethylene using molecular dynamics simulations. Phys. Rev. B 82, 144308 (2010). https://doi.org/10.1103/PhysRevB.82.144308
D. Segal, A. Nitzan, P. Hänggi, Thermal conductance through molecular wires. J. Chem. Phys. 119(13), 6840–6855 (2003). https://doi.org/10.1063/1.1603211
Q. Li, I. Duchemin, S. Xiong, G.C. Solomon, D. Donadio, Mechanical tuning of thermal transport in a molecular junction. J. Phys. Chem. C 119(43), 24636–24642 (2015). https://doi.org/10.1021/acs.jpcc.5b07429
S. Shen, A. Henry, J. Tong, R. Zheng, G. Chen, Polyethylene nanofibres with very high thermal conductivities. Nat. Nanotechnol. 5(4), 251–255 (2010). https://doi.org/10.1038/nnano.2010.27
J. Hone, M. Whitney, C. Piskoti, A. Zettl, Thermal conductivity of single-walled carbon nanotubes. Phys. Rev. B 59(4), 2514–2516 (1999). https://doi.org/10.1103/PhysRevB.59.R2514
P. Kim, L. Shi, A. Majumdar, P.L. McEuen, Thermal transport measurements of individual multiwalled nanotubes. Phys. Rev. Lett. 87(21), 215502 (2001). https://doi.org/10.1103/PhysRevLett.87.215502
E. Pop, D. Mann, Q. Wang, K. Goodson, H. Dai, Thermal conductance of an individual single-wall carbon nanotube above room temperature. Nano Lett. 6(1), 96–100 (2006). https://doi.org/10.1021/nl052145f
S. Berber, Y.-K. Kwon, D. Tománek, Unusually high thermal conductivity of carbon nanotubes. Phys. Rev. Lett. 84(20), 4613–4616 (2000). https://doi.org/10.1103/PhysRevLett.84.4613
J.F. Moreland, J.B. Freund, G. Chen, The disparate thermal conductivity of carbon nanotubes and diamond nanowires studied by atomistic simulation. Microscale Thermophys. Eng. 8(1), 61–69 (2004). https://doi.org/10.1080/10893950490272939
N. Mingo, D.A. Broido, Length dependence of carbon nanotube thermal conductivity and the “problem of long wave’’. Nano Lett. 5(7), 1221–1225 (2005). https://doi.org/10.1021/nl050714d
Z. Yao, J.-S. Wang, B. Li, G.-R. Liu, Thermal conduction of carbon nanotubes using molecular dynamics. Phys. Rev. B 71(8), 085417 (2005). https://doi.org/10.1103/PhysRevB.71.085417
G. Zhang, B. Li, Thermal conductivity of nanotubes revisited: effects of chirality, isotope impurity, tube length, and temperature. J. Chem. Phys. 123(11), 114714 (2005). https://doi.org/10.1063/1.2036967
J. Shiomi, S. Maruyama, Non-Fourier heat conduction in a single-walled carbon nanotube: classical molecular dynamics simulations. Phys. Rev. B 73(20), 205420 (2006). https://doi.org/10.1103/PhysRevB.73.205420
J.R. Lukes, H. Zhong, Thermal conductivity of individual single-wall carbon nanotubes. J. Heat Transf. 129(6), 705–716 (2007). https://doi.org/10.1115/1.2717242
D. Donadio, G. Galli, Thermal conductivity of isolated and interacting carbon nanotubes: comparing results from molecular dynamics and the Boltzmann transport equation. Phys. Rev. Lett. 99(25), 255502 (2007). https://doi.org/10.1103/PhysRevLett.99.255502
M. Alaghemandi, E. Algaer, M.C. Böhm, F. Müller-Plathe, The thermal conductivity and thermal rectification of carbon nanotubes studied using reverse non-equilibrium molecular dynamics simulations. Nanotechnology 20(11), 115704 (2009). https://doi.org/10.1088/0957-4484/20/11/115704
A.V. Savin, B. Hu, Y.S. Kivshar, Thermal conductivity of single-walled carbon nanotubes. Phys. Rev. B 80(19), 195423 (2009). https://doi.org/10.1103/PhysRevB.80.195423
J.A. Thomas, R.M. Iutzi, A.J.H. McGaughey, Thermal conductivity and phonon transport in empty and water-filled carbon nanotubes. Phys. Rev. B 81(4), 045413 (2010). https://doi.org/10.1103/PhysRevB.81.045413
A. Cao, J. Qu, Size dependent thermal conductivity of single-walled carbon nanotubes. J. Appl. Phys. 112(1), 013503 (2012). https://doi.org/10.1063/1.4730908
K. Sääskilahti, J. Oksanen, S. Volz, J. Tulkki, Frequency-dependent phonon mean free path in carbon nanotubes from nonequilibrium molecular dynamics. Phys. Rev. B 91(11), 115426 (2015). https://doi.org/10.1103/PhysRevB.91.115426
R.N. Salaway, L.V. Zhigilei, Molecular dynamics simulations of thermal conductivity of carbon nanotubes: resolving the effects of computational parameters. Int. J. Heat Mass Transf. 70, 954–964 (2014). https://doi.org/10.1016/j.ijheatmasstransfer.2013.11.065
L.F.C. Pereira, I. Savić, D. Donadio, Thermal conductivity of one-, two- and three-dimensional sp \(^{2}\) carbon. N. J. Phys. 15(10), 105019 (2013). https://doi.org/10.1088/1367-2630/15/10/105019
Z. Fan, L.F.C. Pereira, H.-Q. Wang, J.-C. Zheng, D. Donadio, A. Harju, Force and heat current formulas for many-body potentials in molecular dynamics simulations with applications to thermal conductivity calculations. Phys. Rev. B 92(9), 094301 (2015). https://doi.org/10.1103/PhysRevB.92.094301
L. Lindsay, D.A. Broido, N. Mingo, Lattice thermal conductivity of single-walled carbon nanotubes: beyond the relaxation time approximation and phonon-phonon scattering selection rules. Phys. Rev. B 80(12), 125407 (2009). https://doi.org/10.1103/PhysRevB.80.125407
L. Lindsay, D.A. Broido, N. Mingo, Diameter dependence of carbon nanotube thermal conductivity and extension to the graphene limit. Phys. Rev. B 82(16), 161402 (2010). https://doi.org/10.1103/PhysRevB.82.161402
D. Bruns, A. Nojeh, A.S. Phani, J. Rottler, Heat transport in carbon nanotubes: length dependence of phononic conductivity from the Boltzmann transport equation and molecular dynamics. Phys. Rev. B 101(19), 195408 (2020). https://doi.org/10.1103/PhysRevB.101.195408
G. Barbalinardo, Z. Chen, H. Dong, Z. Fan, D. Donadio, Ultrahigh convergent thermal conductivity of carbon nanotubes from comprehensive atomistic modeling. Phys. Rev. Lett. 127(2), 025902 (2021). https://doi.org/10.1103/PhysRevLett.127.025902
D. Bruns, A. Nojeh, A.S. Phani, J. Rottler, Comment on “Ultrahigh convergent thermal conductivity of carbon nanotubes from comprehensive atomistic modeling’’. Phys. Rev. Lett. 128(25), 259601 (2022). https://doi.org/10.1103/PhysRevLett.128.259601
G. Barbalinardo, Z. Chen, H. Dong, Z. Fan, D. Donadio, Barbalinardo et al.: Reply. Phys. Rev. Lett. 128(25), 259602 (2022). https://doi.org/10.1103/PhysRevLett.128.259602
J. Maassen, M. Lundstrom, Steady-state heat transport: ballistic-to-diffusive with Fourier’s law. J. Appl. Phys. 117(3), 035104 (2015). https://doi.org/10.1063/1.4905590
D. Bruns, A. Nojeh, A.S. Phani, J. Rottler, Nanotube heat conductors under tensile strain: reducing the three-phonon scattering strength of acoustic phonons. Phys. Rev. B 104(7), 075440 (2021). https://doi.org/10.1103/PhysRevB.104.075440
A.A. Balandin, Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 10(8), 569–581 (2011)
X. Xu, L.F.C. Pereira, Y. Wang, J. Wu, K. Zhang, X. Zhao, S. Bae, C. Tinh Bui, R. Xie, J.T.L. Thong, B.H. Hong, K.P. Loh, D. Donadio, B. Li, B. Özyilmaz, Length-dependent thermal conductivity in suspended single-layer graphene. Nat. Commun. 5(1), 3689 (2014). https://doi.org/10.1038/ncomms4689
G. Barbarino, C. Melis, L. Colombo, Intrinsic thermal conductivity in monolayer graphene is ultimately upper limited: a direct estimation by atomistic simulations. Phys. Rev. B 91(3), 035416 (2015). https://doi.org/10.1103/PhysRevB.91.035416
G. Fugallo, A. Cepellotti, L. Paulatto, M. Lazzeri, N. Marzari, F. Mauri, Thermal conductivity of graphene and graphite: collective excitations and mean free paths. Nano Lett. 14(11), 6109–6114 (2014). https://doi.org/10.1021/nl502059f
Z. Fan, L.F.C. Pereira, P. Hirvonen, M.M. Ervasti, K.R. Elder, D. Donadio, T. Ala-Nissila, A. Harju, Thermal conductivity decomposition in two-dimensional materials: application to graphene. Phys. Rev. B 95(14), 144309 (2017). https://doi.org/10.1103/PhysRevB.95.144309
Z. Fan, P. Hirvonen, L.F.C. Pereira, M.M. Ervasti, K.R. Elder, D. Donadio, A. Harju, T. Ala-Nissila, Bimodal grain-size scaling of thermal transport in polycrystalline graphene from large-scale molecular dynamics simulations. Nano Lett. 17(10), 5919–5924 (2017). https://doi.org/10.1021/acs.nanolett.7b01742
S. Lee, D. Broido, K. Esfarjani, G. Chen, Hydrodynamic phonon transport in suspended graphene. Nat. Commun. 6(1), 6290 (2015). https://doi.org/10.1038/ncomms7290
N. Bonini, J. Garg, N. Marzari, Acoustic phonon lifetimes and thermal transport in free-standing and strained graphene. Nano Lett. 12(6), 2673–2678 (2012). https://doi.org/10.1021/nl202694m
Y. Kuang, L. Lindsay, S. Shi, X. Wang, B. Huang, Thermal conductivity of graphene mediated by strain and size. Int. J. Heat Mass Transf. 101, 772–778 (2016). https://doi.org/10.1016/j.ijheatmasstransfer.2016.05.072
A. Majumdar, Microscale heat conduction in dielectric thin films. J. Heat Transf. 115(1), 7–16 (1993). https://doi.org/10.1115/1.2910673
K.M. Hoogeboom-Pot, J.N. Hernandez-Charpak, X. Gu, T.D. Frazer, E.H. Anderson, W. Chao, R.W. Falcone, R. Yang, M.M. Murnane, H.C. Kapteyn, D. Nardi, A new regime of nanoscale thermal transport: collective diffusion increases dissipation efficiency. Proc. Natl. Acad. Sci. 112, 4846–4851 (2015)
K.T. Regner, D.P. Sellan, Z. Su, C.H. Amon, A.J.H. McGaughey, J.A. Malen, Broadband phonon mean free path contributions to thermal conductivity measured using frequency domain thermoreflectance. Nat. Commun. 4(1), 1640 (2013). https://doi.org/10.1038/ncomms2630
H. Zhang, X. Chen, Y.-D. Jho, A.J. Minnich, Temperature-dependent mean free path spectra of thermal phonons along the c-axis of graphite. Nano Lett. 16, 7 (2016)
A. Sood, F. Xiong, S. Chen, R. Cheaito, F. Lian, M. Asheghi, Y. Cui, D. Donadio, K.E. Goodson, E. Pop, Quasi-ballistic thermal transport across MoS \(_{{\rm 2}}\) thin films. Nano Lett. 19(4), 2434–2442 (2019). https://doi.org/10.1021/acs.nanolett.8b05174
G. Chen, T. Zeng, Nonequilibrium phonon and electron transport in heterostructures and superlattices. Microscale Thermophys. Eng. 5(2), 71–88 (2001). https://doi.org/10.1080/108939501750397436
J. Maassen, M. Lundstrom, A simple Boltzmann transport equation for ballistic to diffusive transient heat transport. J. Appl. Phys. 117(13), 135102 (2015). https://doi.org/10.1063/1.4916245
J. Kaiser, T. Feng, J. Maassen, X. Wang, X. Ruan, M. Lundstrom, Thermal transport at the nanoscale: a Fourier’s law vs. phonon Boltzmann equation study. J. Appl. Phys. 121(4), 044302 (2017). https://doi.org/10.1063/1.4974872
R.A. Guyer, J.A. Krumhansl, Solution of the linearized phonon Boltzmann equation. Phys. Rev. 148(2), 766–778 (1966). https://doi.org/10.1103/PhysRev.148.766
Y. Guo, M. Wang, Phonon hydrodynamics and its applications in nanoscale heat transport. Phys. Rep. 595, 1–44 (2015)
P. Torres, A. Torelló, J. Bafaluy, J. Camacho, X. Cartoixà, F.X. Alvarez, First principles kinetic-collective thermal conductivity of semiconductors. Phys. Rev. B 95, 165407 (2017). https://doi.org/10.1103/PhysRevB.95.165407
P. Torres, A. Ziabari, A. Torelló, J. Bafaluy, J. Camacho, X. Cartoixà, A. Shakouri, F.X. Alvarez, Emergence of hydrodynamic heat transport in semiconductors at the nanoscale. Phys. Rev. Mater. 2(7), 076001 (2018). https://doi.org/10.1103/PhysRevMaterials.2.076001
L. Sendra, A. Beardo, P. Torres, J. Bafaluy, F.X. Alvarez, J. Camacho, Derivation of a hydrodynamic heat equation from the phonon Boltzmann equation for general semiconductors. Phys. Rev. B 103(14), 140301 (2021). https://doi.org/10.1103/PhysRevB.103.L140301
B. Vermeersch, A.M.S. Mohammed, G. Pernot, Y.R. Koh, A. Shakouri, Superdiffusive heat conduction in semiconductor alloys—II. Truncated Lévy formalism for experimental analysis. Phys. Rev. B 91(8), 085203 (2015). https://doi.org/10.1103/PhysRevB.91.085203
P. Torres, A. Mohammed, I. Torelló, J. Bafaluy, J. Camacho, X. Cartoixà, A. Shakouri, F. XavierAlvarez, Collective thermal transport in pure and alloy semiconductors. Phys. Chem. Chem. Phys. 20(10), 6805–6810 (2018). https://doi.org/10.1039/C7CP07738F
A. Beardo, S. Alajlouni, L. Sendra, J. Bafaluy, A. Ziabari, Y. Xuan, J. Camacho, A. Shakouri, F.X. Alvarez, Hydrodynamic thermal transport in silicon at temperatures ranging from 100 to 300 K. Phys. Rev. B 105(16), 165303 (2022). https://doi.org/10.1103/PhysRevB.105.165303
M. Simoncelli, N. Marzari, A. Cepellotti, Generalization of Fourier’s law into viscous heat equations. Phys. Rev. X 10(1), 011019 (2020). https://doi.org/10.1103/PhysRevX.10.011019
A. Sellitto, I. Carlomagno, D. Jou, Two-dimensional phonon hydrodynamics in narrow strips. Proc. R. Soc. A Math. Phys. Eng. Sci. 471(2182), 20150376 (2015)
Y. Guo, M. Wang, Phonon hydrodynamics for nanoscale heat transport at ordinary temperatures. Phys. Rev. B 97(3), 035421 (2018). https://doi.org/10.1103/PhysRevB.97.035421
Y. He, G. Galli, Microscopic origin of the reduced thermal conductivity of silicon nanowires. Phys. Rev. Lett. 108(21), 215901 (2012). https://doi.org/10.1103/PhysRevLett.108.215901
I. Duchemin, D. Donadio, Atomistic simulations of heat transport in real-scale silicon nanowire devices. Appl. Phys. Lett. 100, 223107 (2012)
S. Neogi, J.S. Reparaz, L.F.C. Pereira, B. Graczykowski, M.R. Wagner, M. Sledzinska, A. Shchepetov, M. Prunnila, J. Ahopelto, C.M. Sotomayor-Torres, D. Donadio, Tuning thermal transport in ultrathin silicon membranes by surface nanoscale engineering. ACS Nano 9(4), 3820–3828 (2015). https://doi.org/10.1021/nn506792d
S. Xiong, D. Selli, S. Neogi, D. Donadio, Native surface oxide turns alloyed silicon membranes into nanophononic metamaterials with ultralow thermal conductivity. Phys. Rev. B 95(18), 180301 (2017). https://doi.org/10.1103/PhysRevB.95.180301
S. Neogi, D. Donadio, Anisotropic in-plane phonon transport in silicon membranes guided by nanoscale surface resonators. Phys. Rev. Appl. 14(2), 024004 (2020). https://doi.org/10.1103/PhysRevApplied.14.024004
D. Segal, Single mode heat rectifier: controlling energy flow between electronic conductors. Phys. Rev. Lett. 100(10), 105901 (2008). https://doi.org/10.1103/PhysRevLett.100.105901
C.R. Otey, W.T. Lau, S. Fan, Thermal rectification through vacuum. Phys. Rev. Lett. 104(15), 154301 (2010). https://doi.org/10.1103/PhysRevLett.104.154301
S. Basu, M. Francoeur, Near-field radiative transfer based thermal rectification using doped silicon. Appl. Phys. Lett. 98(11), 113106 (2011). https://doi.org/10.1063/1.3567026
K. Joulain, Y. Ezzahri, J. Drevillon, B. Rousseau, D.D.S. Meneses, Radiative thermal rectification between SiC and SiO\(_{\rm 2}\). Opt. Express 23(24), 1388–1397 (2015). https://doi.org/10.1364/OE.23.0A1388
M.J. Martínez-Pérez, A. Fornieri, F. Giazotto, Rectification of electronic heat current by a hybrid thermal diode. Nat. Nanotechnol. 10(4), 303–307 (2015). https://doi.org/10.1038/nnano.2015.11
J. Ordonez-Miranda, Y. Ezzahri, K. Joulain, Quantum thermal diode based on two interacting spinlike systems under different excitations. Phys. Rev. E 95(2), 022128 (2017). https://doi.org/10.1103/PhysRevE.95.022128
L.-A. Wu, D. Segal, Sufficient conditions for thermal rectification in hybrid quantum structures. Phys. Rev. Lett. 102(9), 095503 (2009). https://doi.org/10.1103/PhysRevLett.102.095503
J. Senior, A. Gubaydullin, B. Karimi, J.T. Peltonen, J. Ankerhold, J.P. Pekola, Heat rectification via a superconducting artificial atom. Commun. Phys. 3(1), 40 (2020). https://doi.org/10.1038/s42005-020-0307-5
S.O. Kasali, J. Ordonez-Miranda, K. Joulain, Optimization of the rectification factor of radiative thermal diodes based on two phase-change materials. Int. J. Heat Mass Transf. 154, 119739 (2020). https://doi.org/10.1016/j.ijheatmasstransfer.2020.119739
H. Wang, S. Hu, K. Takahashi, X. Zhang, H. Takamatsu, J. Chen, Experimental study of thermal rectification in suspended monolayer graphene. Nat. Commun. 8(1), 15843 (2017). https://doi.org/10.1038/ncomms15843
W.-R. Zhong, W.-H. Huang, X.-R. Deng, B.-Q. Ai, Thermal rectification in thickness-asymmetric graphene nanoribbons. Appl. Phys. Lett. 99(19), 193104 (2011). https://doi.org/10.1063/1.3659474
M. Muñoz Rojo, Z. Li, C. Sievers, A.C. Bornstein, E. Yalon, S. Deshmukh, S. Vaziri, M.-H. Bae, F. Xiong, D. Donadio, E. Pop, Thermal transport across graphene step junctions. 2D Mater. 6(1), 011005 (2018)
Y. Wang, S. Chen, X. Ruan, Tunable thermal rectification in graphene nanoribbons through defect engineering: a molecular dynamics study. Appl. Phys. Lett. 100(16), 163101 (2012). https://doi.org/10.1063/1.3703756
S. Hu, M. An, N. Yang, B. Li, A series circuit of thermal rectifiers: an effective way to enhance rectification ratio. Small 13(6), 1602726 (2017). https://doi.org/10.1002/smll.201602726
J. Hu, X. Ruan, Y.P. Chen, Thermal conductivity and thermal rectification in graphene nanoribbons: a molecular dynamics study. Nano Lett. 9(7), 2730–2735 (2009). https://doi.org/10.1021/nl901231s
N. Yang, G. Zhang, B. Li, Thermal rectification in asymmetric graphene ribbons. Appl. Phys. Lett. 95(3), 033107 (2009). https://doi.org/10.1063/1.3183587
N. Yang, G. Zhang, B. Li, Carbon nanocone: a promising thermal rectifier. Appl. Phys. Lett. 93(24), 243111 (2008). https://doi.org/10.1063/1.3049603
X.-K. Chen, J. Liu, Z.-X. Xie, Y. Zhang, Y.-X. Deng, K.-Q. Chen, A local resonance mechanism for thermal rectification in pristine/branched graphene nanoribbon junctions. Appl. Phys. Lett. 113(12), 121906 (2018). https://doi.org/10.1063/1.5053233
X. Yang, D. Yu, B. Cao, A.C. To, Ultrahigh thermal rectification in pillared graphene structure with carbon nanotube-graphene intramolecular junctions. ACS Appl. Mater. Interfaces 9(1), 29–35 (2017). https://doi.org/10.1021/acsami.6b12853
X. Yang, S. Wu, J. Xu, D. Yu, B. Cao, Enhancing thermal rectification in graphene-carbon nanotube junctions by tuning the chirality of pillar. EPL 123(4), 44004 (2018). https://doi.org/10.1209/0295-5075/123/44004
M. Alaghemandi, F. Leroy, F. Müller-Plathe, M.C. Böhm, Thermal rectification in nanosized model systems: a molecular dynamics approach. Phys. Rev. B 81(12), 125410 (2010). https://doi.org/10.1103/PhysRevB.81.125410
X. Cartoixà, L. Colombo, R. Rurali, Thermal rectification by design in telescopic Si nanowires. Nano Lett. 15(12), 8255–8259 (2015). https://doi.org/10.1021/acs.nanolett.5b03781
R. Dettori, C. Melis, R. Rurali, L. Colombo, Thermal rectification in silicon by a graded distribution of defects. J. Appl. Phys. 119(21), 215102 (2016). https://doi.org/10.1063/1.4953142
K.R. Hahn, C. Melis, L. Colombo, Thermal conduction and rectification phenomena in nanoporous silicon membranes. Phys. Chem. Chem. Phys. 24(22), 13625–13632 (2022). https://doi.org/10.1039/D2CP00775D
F. Yousefi, M. Shavikloo, M. Mohammadi, Non-equilibrium molecular dynamics study on radial thermal conductivity and thermal rectification of graphene. Mol. Simul. 45(8), 646–651 (2019). https://doi.org/10.1080/08927022.2019.1578354
W. Zheng, C.J. McClellan, E. Pop, Y.K. Koh, Nonequilibrium phonon thermal resistance at MoS \(_{\rm 2 }\) /oxide and graphene/oxide interfaces. ACS Appl. Mater. Interfaces 14(19), 22372–22380 (2022). https://doi.org/10.1021/acsami.2c02062
W.G. Hoover, Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31(3), 1695–1697 (1985). https://doi.org/10.1103/PhysRevA.31.1695
P. Jiang, S. Hu, Y. Ouyang, W. Ren, C. Yu, Z. Zhang, J. Chen, Remarkable thermal rectification in pristine and symmetric monolayer graphene enabled by asymmetric thermal contact. J. Appl. Phys. 127(23), 235101 (2020). https://doi.org/10.1063/5.0004484
G.J. Martyna, M.L. Klein, M. Tuckerman, Nosé-Hoover chains: the canonical ensemble via continuous dynamics. J. Chem. Phys. 97(4), 2635–2643 (1992). https://doi.org/10.1063/1.463940
M. Alaghemandi, F. Leroy, E. Algaer, M.C. Böhm, F. Müller-Plathe, Thermal rectification in mass-graded nanotubes: a model approach in the framework of reverse non-equilibrium molecular dynamics simulations. Nanotechnology 21(7), 075704 (2010). https://doi.org/10.1088/0957-4484/21/7/075704
C.-W. Chang, Experimental probing of non-Fourier thermal conductors, in Thermal Transport in Low Dimensions: From Statistical Physics to Nanoscale Heat Transfer. ed. by S. Lepri (Springer, Berlin, 2016), pp.305–338
C.W. Chang, D. Okawa, H. Garcia, A. Majumdar, A. Zettl, Breakdown of Fourier’s law in nanotube thermal conductors. Phys. Rev. Lett. 101(7), 075903 (2008). https://doi.org/10.1103/PhysRevLett.101.075903
V. Lee, C.-H. Wu, Z.-X. Lou, W.-L. Lee, C.-W. Chang, Divergent and ultrahigh thermal conductivity in millimeter-long nanotubes. Phys. Rev. Lett. 118(13), 135901 (2017)
Q.-Y. Li, K. Takahashi, X. Zhang, Comment on “divergent and ultrahigh thermal conductivity in millimeter-long nanotubes’’. Phys. Rev. Lett. 119(17), 179601 (2017)
S. Huberman, R.A. Duncan, K. Chen, B. Song, V. Chiloyan, Z. Ding, A.A. Maznev, G. Chen, K.A. Nelson, Observation of second sound in graphite at temperatures above 100 K. Science 364(6438), 375–379 (2019). https://doi.org/10.1126/science.aav3548
J. Maire, R. Anufriev, R. Yanagisawa, A. Ramiere, S. Volz, M. Nomura, Heat conduction tuning by wave nature of phonons. Sci. Adv. 3(8), 1700027 (2017)
M. Nomura, R. Anufriev, Z. Zhang, J. Maire, Y. Guo, R. Yanagisawa, S. Volz, Review of thermal transport in phononic crystals. Mater. Today Phys. 22, 100613 (2022). https://doi.org/10.1016/j.mtphys.2022.100613
T. Meier, F. Menges, P. Nirmalraj, H. Hölscher, H. Riel, B. Gotsmann, Length-dependent thermal transport along molecular chains. Phys. Rev. Lett. 113(6), 060801 (2014)
L. Yang, Y. Tao, Y. Zhu, M. Akter, K. Wang, Z. Pan, Y. Zhao, Q. Zhang, Y.-Q. Xu, R. Chen et al., Observation of superdiffusive phonon transport in aligned atomic chains. Nat. Nanotechnol. 16(7), 764–768 (2021)
L. Cui, S. Hur, Z.A. Akbar, J.C. Klöckner, W. Jeong, F. Pauly, S.-Y. Jang, P. Reddy, E. Meyhofer, Thermal conductance of single-molecule junctions. Nature 572(7771), 628–633 (2019)
Z.-C. Mao, Y.-Z. Xu, Q.-X. Mei, W.-D. Zhao, Y. Jiang, Z.-J. Cheng, X.-Y. Chang, L. He, L. Yao, Z.-C. Zhou, Y.-K. Wu, L.-M. Duan, Observation of anomalous heat transport in a trapped ion chain. Phys. Rev. A 105, 033107 (2022). https://doi.org/10.1103/PhysRevA.105.033107
G. Benenti, G. Casati, D. Rossini, G. Strini, Principles of Quantum Computation and Information (A Comprehensive Textbook) (World Scientific, Singapore, 2019). https://www.worldscientific.com/worldscibooks/10.1142/10909
P. Talkner, P. Hänggi, Colloquium: Statistical mechanics and thermodynamics at strong coupling: quantum and classical. Rev. Mod. Phys. 92, 041002 (2020). https://doi.org/10.1103/RevModPhys.92.041002
A. Auffèves, Quantum technologies need a quantum energy initiative. PRX Quantum 3, 020101 (2022). https://doi.org/10.1103/PRXQuantum.3.020101
Acknowledgements
GB, SL, DD, and RL acknowledge the contribution of the coauthors with whom they worked on the topics here reviewed, notably G. Casati, S. Chen, P.F. Di Cintio, S. Iubini, C. Mejía-Monasterio, A. Politi, K. Saito, J. Wang, L.F.C. Pereira, S. Neogi, S. Xiong, Z. Fan, Z. Chen, and G. Barbalinardo.
Funding
Open access funding provided by Consiglio Nazionale Delle Ricerche (CNR) within the CRUI-CARE Agreement. This work is part of the MIUR-PRIN2017 project Coarse-grained description for non-equilibrium systems and transport phenomena (CO-NEST) No. 201798CZL.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the work. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Benenti, G., Donadio, D., Lepri, S. et al. Non-Fourier heat transport in nanosystems. Riv. Nuovo Cim. 46, 105–161 (2023). https://doi.org/10.1007/s40766-023-00041-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40766-023-00041-w