Introduction

In reality, many problems can be abstracted as constrained multiobjective optimization problems (CMOPs), for example, city programming, engineering design, investment decision and control system design [1, 2]. There are often multiple goals and multiple constraints in these problems, and the development of one goal is often accompanied by the decay of one or more other goals. For a particular example, the vehicle routing problem with time windows aims to find the solutions minimizing both the number of vehicles and the total traveled distance, in which the solutions should also satisfy the time windows of customers and capacities of vehicles. Due to the strict constraints of time windows and capacities, it is difficult to find many feasible solutions for the problem; hence, the optimization of the number of vehicles and total traveled distance becomes very challenging. Without loss of generality, a CMOP can be defined as follows [3]:

$$\begin{aligned} \begin{aligned}&\textrm{minimize} \quad{} & {} \textbf{F}\left( \textbf{x} \right) =\left( f_1\left( \textbf{x} \right) ,f_2\left( \textbf{x} \right) ,...,f_M\left( \textbf{x} \right) \right) ^{{T}} \\&\mathrm {subject\;to}\quad{} & {} g_i\left( \textbf{x} \right) \leqslant 0,i=1,...,p \\&\,\,{} & {} h_j\left( \textbf{x} \right) =0,j=1,...,q \\&\;{} & {} \textbf{x}\in \varOmega , \end{aligned} \end{aligned}$$
(1)

where \(\textbf{x}=\left( x_1,...,x_D \right) ^T\in \varOmega \) is a solution consisting of D decision variables; \(\varOmega \in R^D\) is the decision space. \(\textbf{F}\left( \textbf{x} \right) \) constitutes M real-valued conflicting objective functions, and \(\textbf{F}\left( \textbf{x} \right) :\varOmega \rightarrow R^M\), \(R^M\) is the objective space. \(g_i\left( \textbf{x} \right) \) are p inequality constraints. \(h_j\left( \textbf{x} \right) \) are q equality constraints. In this paper, we only consider minimization problems.

There is usually more than one constraint, so a metric to describe the extent to which a solution \(\textbf{x}\) violates the constraints is used in this paper. The overall constraint violation value of a solution \(\textbf{x}\) is defined as

$$\begin{aligned} {\text {CV}}\left( \textbf{x} \right)&=\sum _{i=1}^p\max \left( 0,g_i\left( \textbf{x} \right) \right) \nonumber \\ {}&\quad +\sum _{j=1}^q{\max \left( 0,|h_j\left( \textbf{x} \right) |-\mathbf {\epsilon } \right) ,} \end{aligned}$$
(2)

where \(\mathbf {\epsilon }\) is a very small positive number (e.g., \(\mathbf {\epsilon }=10^{-4}\)) to relax the equality constraints. On the basis of this definition, if CV\(\left( \textbf{x} \right) = 0 \) , then \(\textbf{x}\) is called a feasible solution. If CV\(\left( \textbf{x} \right) > 0 \), \(\textbf{x}\) is an infeasible solution. The objective space whose solutions are all feasible is called the feasible region; otherwise, it is called the infeasible region.

Considering multiobjective minimum optimization problems, for two solutions \(\textbf{x}_1\) and \(\textbf{x}_2\), \(\textbf{x}_1\) is said to Pareto dominate \(\textbf{x}_2\) (denoted as \(\textbf{x}_1\prec \textbf{x}_2\)) if \(\textbf{x}_1\) is not greater than \(\textbf{x}_2\) and \(\textbf{x}_1\) has at least one smaller objective. If a solution is not dominated by any other solutions, it is a nondominated solution, or it can be called a Pareto-optimal solution. All the nondominated solutions of a CMOP consist of the Pareto set (PS). The mapping of the PS in the objective space is the Pareto front (PF). Moreover, the PF of a CMOP is a constrained PF (CPF) when the constraints are considered. Otherwise, it is an unconstrained PF (UPF).

As a zero-order optimization method, evolutionary algorithms (EAs) can be used in the case of discontinuous objective functions, within disjoined and/or nonconvex design spaces, and together with discrete, continuous or integer design variables [4]. EAs can obtain multiple optimal solutions in a single simulation, so it is very suitable for solving multiobjective problems. Various multiobjective evolutionary algorithms (MOEAs) have been proposed, such as NSGA-II [5], which is based on Pareto dominance, MOEA/D [6], which is based on decomposition, and SMS-EMOA [7], which is based on indicators. Moreover, there are algorithms to enhance performance by integrating memetic concept or information feedback, such as IMOMA-II [8] and MOEA/D-IFM [9].

EAs are also very suitable for solving CMOPs. Compared with unconstrained multiobjective optimization problems (UCMOPs), the difficulty of CMOPs lies in the processing of constraints. When the constraints are added to the unconstrained problem, the original feasible region may become narrow and unconnected, and the PF may become discontinuous or even completely infeasible, which causes substantial difficulties in searching for solutions and converging to the final PF [10]. Over the past two decades, many researchers have devoted themselves to solving CMOPs using evolutionary computing theory and have developed various constrained multiobjective evolutionary algorithms (CMOEAs). They are described in detail in the next section.

Table 1 A summary of the advantages and limitations of the existing CMOEAs
Full size table

The ultimate goal of constrained multiobjective optimization is to obtain a feasible PF for a given problem. It is evident that the CPF is often at the boundary between feasible and infeasible regions. Thus, how one should use infeasible and feasible solutions is key in CMOPs [11]. In recent years, many CMOEAs have attempted to retain the potential infeasible solutions and make use of them appropriately [11,12,13]. Although these different strategies have achieved some success, they still face the following issues.

  • Most algorithms simply rely on infeasible solutions to enrich the diversity of the population and lack the driving force to explore infeasible solutions near the CPF.

  • When the CPF coincides with the UPF, some algorithms can only utilize solutions from feasible region to search for Pareto-optimal solutions, which makes it challenging for the population to traverse the infeasible region.

To address the first issue, this paper proposes an operation called reverse search. The population conducting reverse search approaches the CPF from the infeasible side of the CPF and gradually obtains an “infeasible constrained PF" consisting entirely of nondominated infeasible solutions. For the second issue, a two-stage strategy is used, which first searches the UPF and then the CPF. Combining the above two points, this paper proposes a novel two-stage bidirectional coevolution algorithm with reverse search named BCRS. The main contributions of this article can be summarized as follows:

  • A new constrained multiobjective optimization algorithm with a concise structure is proposed. The algorithm consists of two stages. In the first stage, the main focus is on finding as many promising solutions as possible, while ignoring constraints. In the second stage, a bidirectional coevolutionary approach is employed to approximate the CPF.

  • A bidirectional coevolution framework with reverse search is proposed. Reverse search considers the original problem as its opposite problem and explores potential solutions near the CPF to coevolve with forward search, facilitating efficient and fast convergence of the main population to the CPF.

  • The proposed algorithm was tested on four benchmark test suites and 15 real-world problems. It demonstrated competitive performance compared to existing state-of-the-art algorithms on the majority of the problems.

The remainder of this article is organized as follows. In “Related work” Section reviews related work on constraint processing techniques (CHTs) and CMOEAs. In “Proposed algorithm” Section, we provide details on the proposed BCRS framework and its concrete implementations. In “Experimental setup” Section presents an experimental study, followed by the results and discussions for the experiment in “Experimental results and analysis” Section. Finally, “Conclusions” Section concludes this article.

Related work

Literature review

In this section, we review some CMOEAs. According to constraint processing techniques, current CMOEAs can be divided into the following four categories. Table 1 summarizes the advantages and limitations of these CMOEAs.

The first category is based on a penalty function. The main idea is to transform the constrained optimization problem into an unconstrained problem by adding the penalty term into objective functions or its variants. How to set the penalty coefficients is the most critical issue for penalty function methods. Penalty coefficients can be static, dynamic or adaptive. The static penalty coefficients remain constant throughout the evolutionary process. However, in this way, the preference between objectives and constraints will remain unchanged in the early and late stages of evolution [10]. For complex problems, it is difficult for this method to achieve ideal results. The dynamic penalty coefficients change according to the generation number. The adaptive penalty coefficients change with certain properties of the population during evolution. The latter two methods can also be regarded as one. They attempt to establish a dynamic rule to make better use of the penalty. However, the establishment of the rule is a problem that needs careful consideration. Ma et al. [14] designed the penalty coefficient according to the proportion of the current feasible solutions. Then, the coefficient is combined with two rankings of individuals based on the objective value and CV to construct a fitness function. Wang et al. [15] proposed MOEA/D-DPF, in which a dynamic penalty function is used during the search. Yu et al. [16] designed a dynamic penalty function and a ranking ignoring constraints to dynamically adjust the selection preference between feasibility and convergence.

The second category separately compares objectives and constraints. Deb et al. [5] proposed the constrained dominance principle (CDP) to solve CMOPs. However, if a solution is an infeasible solution in the CDP, it is considered worse than a feasible solution, which makes the search easily fall into local optimum. To improve the CDP and release more infeasible solutions to participate in evolution, a \(\varepsilon \) constrained method [17] is proposed. The \(\varepsilon \) method relaxes the definition of the infeasible solution in the CDP. A solution \(\textbf{x}\) in the decision space, if CV\(\left( \textbf{x} \right) \leqslant \varepsilon \), is considered to be a feasible solution, where \(\varepsilon \) is a parameter and will be gradually reduced with evolution. Wang et al. [18] embedded niche strategies into the \(\varepsilon \) constrained method to ensure the diversity of Pareto solutions. Stochastic ranking (SR) [19] is another representative method to separately compare objectives and constraints. In this method, when two solutions are compared, there is a probability pf of ignoring CV and a probability \((1-pf)\) of considering CV, which reduces the preference of selection for feasible solutions. To dynamically adjust the probability parameters, Ying et al. [20] proposed an adaptive SR mechanism according to the evolutionary stage and the degrees of constraint violation of individuals.

The third category combines EA with mathematical programming (MP). EA is effective at finding promising solutions from global perspectives, but in local areas, MP can perform subtle search. Datta et al. [21] used radial boundary intersection to decompose the nonconvex nonlinear optimization problem into subproblems that find the solutions along the rays and combined it with an interior point method. Schütze et al. [22] proposed a method of combining the gradient subspace approximation (GSA) with EA, which can use neighborhood information given by EA and reduce the cost of local search. Equality constraints can reduce the dimension of the feasible region, which causes problems for evolutionary computation. Cuate et al. [23] hybridized the multiobjective evolutionary algorithm with continuation-like techniques to obtain a fast and reliable numerical solver that is highly competitive on equality-constrained multiobjective problems. Cantú et al. [24] studied the effect of repairing infeasible solutions using the gradient information for solving CMOPs.

The fourth category transforms CMOPs into other problems. This method mainly transforms the original problem into a multipopulation cooperative optimization problem or a multistage problem. For example, Fan et al. [25] developed a framework push and pull search (PPS) to divide the search process into the push stage and the pull stage. In the push stage, constraints are completely ignored and an MOEA is used to explore the UPF. Then, in the pull stage, the solutions found in the push stage are evolved toward the CPF by the CMOP, which considers constraints. Li et al. [26] proposed C-TAEA, which has two populations named the convergence-oriented archive (CA) to push the population toward the PF and diversity-oriented archive (DA) to maintain the population diversity. Tian et al. [12] proposed a weak cooperation framework in CCMO which cooperates the population 1 evaluated by the origin CMOP with the population 2 evolving according to a helper problem derived from the origin CMOP by only sharing all the offspring in each generation. Liu et al. [11] proposed a CMOEA named BiCo with bidirectional coevolution. BiCo maintains two populations and searches for solutions surrounding the boundary of the feasible region and infeasible region. In PDTP-MDE, Yu et al. [27] divided the whole evolution process into two sequential phases. The first stage uses shift-based density estimation as the main criterion for balancing convergence and diversity but takes feasibility as the auxiliary indicator. Thereafter, the second stage may adopt two different methods to introduce infeasible solutions for maintaining feasibility and diversity according to the population status in the first stage. AT-CMOEA [28] is also a two-stage approach characterized by the coevolution between the main population and assistant in the first stage. To maintain the diversity and feasibility of the search, the main population may cross through the infeasible region by ignoring all constraints while the assistant population takes all constraint violations as an additional objective to select promising solutions. Dong et al. [29] proposed a two-stage algorithm that emphasizes convergence, diversity, and feasibility differently in different stages. Qiao et al. [30] used evolutionary multitasking (EMT) to solve CMOPs. In EMCMO, the useful knowledge is found by the designed tentative method and transferred to improve the performance of the two tasks. To balance constraint satisfaction and objective optimization, Yang et al. [31] proposed a dual-population evolutionary algorithm called dp-ACS. In this algorithm, a new dominance relation and an adaptive constraint strength strategy are presented. Zhang et al. [32] proposed MSCEA to solve CMOPs by addressing a series of constraint-centric problems derived from the original problem at multiple stages with their constraint boundaries shrinking gradually. Qiao et al. [13] converted a CMOP into an multitasking problem and used an auxiliary task with a dynamic descent constraint boundary to help main task enter into feasible regions. Zou et al. [33] used C+2 (C is the number of constraints) populations to solve CMOPs. Furthermore, activation dormancy detection (ADD) and combine occasion detection (COD) is proposed to accelerate the optimization and find the appropriate time to find the SubCPF.

Symbols

For the convenience of intuitive understanding, the main abbreviations, variables, and adjustable control parameters in this paper are listed in Table 2.

Table 2 Symbols
Full size table
Fig. 1
figure 1

The framework of BCRS

Full size image

Proposed algorithm

General framework

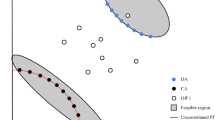
For most CMOPs, there are large regions of infeasible space in their objective space. BCRS seeks to extract information from the infeasible domain and identify promising infeasible solutions to participate in the evolution process. The framework of BCRS is illustrated in Fig. 1 and Algorithm 1.

It employs a two-stage approach, where the search process is divided into two parts. In the first stage, all constraints are ignored with the aim of increasing solution diversity and driving the population toward the region where feasible solutions are likely to be found. In the second stage, constraints are considered, and a bidirectional coevolution is employed to handle the constraints. It maintains evolution in two directions. The population in the first direction searches for promising solutions from the feasible domain. This population is referred to as the main population. The guiding principle for the evolution of the main population is to retain feasible and discard infeasible solutions. Detailed explanations are provided in “The second stage” Section. The other direction is the infeasible direction. In this direction, the original problem is considered as the reverse problem for the evolution of the population. For instance, if the original problem was a minimization problem, it becomes a maximization problem in this direction. The purpose of this population’s evolution is to approach the CPF from the infeasible domain and obtain infeasible solutions with better distribution and convergence to the CPF. In “Computational complexity of BCRS” Section provides a detailed explanation of this process.

As shown in Fig. 2, the two populations approach the CPF from the feasible and infeasible side of the CPF. They exchange information with each other during the evolution to drive the main population toward an approximation of the CPF with better convergence and distribution characteristics.

Fig. 2
figure 2

Illustration of bidirectional coevolution

Full size image
Algorithm 1
figure b

The general framework of BCRS

Full size image

The first stage

In the first stage, the constraints are ignored, and a algorithm based on decomposition [6] is used to evolve the population. The algorithm decomposes the multiobjective optimization problem (MOP) into a set of subproblems using weight vectors and designs a decomposition function for each subproblem. These decomposition functions are used to determine whether an individual survives into the next generation. In this paper, we adopt the Tchebycheff decomposition method to decompose the problem. The decomposition function for ith subproblem is as follows:

$$\begin{aligned} g^{te}\left( \textbf{x},\lambda ^i,z^* \right) =\underset{j=1,...,M}{\max }\lambda _{j}^{i} |f_j\left( \textbf{x} \right) -z_{j}^{*}|, \end{aligned}$$
(3)

where \(\lambda ^i=\left( \lambda _{1}^{i},...,\lambda _{M}^{i} \right) \) is a weight vector and \(\lambda _{1}^{i}+\cdots +\lambda _{M}^{i}=1\), \(\lambda _{j}^{i}>0\), \(i =1,...,N\). \(z^*=\left( z_{1}^{*},...,z_{M}^{*} \right) \) is the ideal point, \(z_{j}^{*}=\min _{k=1,...,N}f_j\left( \textbf{x}^k \right) \). Algorithm 2 describes the procedure of the first stage. The first-stage algorithm proposed here has a closer resemblance to MOEA/D-DE [34] in terms of its workflow. In line 2, \(\delta \) is the probability of selection from neighbors, and it is set to 0.9 [34]. In line 7, the offspring \(\textbf{y}^i\) is generated by alternately using the genetic algorithm and differential evolution during the evolution. This allows the first stage to search for more diverse solutions without increasing algorithm complexity. In lines 9–14, to enhance the diversity of the search, only one neighbor of a subproblem with larger Tchebycheff value than the offspring is randomly selected for replacement. The size of the neighborhood is set to 10.

In line 3 of Algorithm 1, when the difference between the sum of all individual objective values of the current populations and that of the previous generation is less than the predefined threshold value \(r_0\) (1e-3 in this paper), it can be considered that the population has reached the UPF. Then, we can switch to the second stage.

The strategy of bidirectional coevolution can be effectively utilized when the CPF of the problem does not coincide with the UPF. However, there are some problems whose CPF and UPF overlap. The strategy of ignoring constraints in the first stage can help BCRS effectively address such problems. Additionally, the first stage can help a population cross a wide range of infeasible fields to approach the CPF while preventing evolution from falling into local optima.

Algorithm 2
figure c

The first-stage strategy

Full size image

The second stage

The evolution in the feasible region

The main population gradually approaches the CPF from within the feasible region. This direction of evolution is called forward evolution. The principle is to eliminate infeasible solutions as much as possible and propel the population toward the feasible region near the CPF. In this paper, a variant of the NSGA-II-CDP is used to evolve the main population. NSGA-II-CDP is one of the most classical CMOEAs and can effectively drive the population toward the PF within the feasible region. The main procedure is depicted in Algorithm 3. The main population P is combined with the offspring \(O_{fd}\) generated from the forward evolution process and the offspring \(O_{rd}\) generated from the reverse evolution process to form a set. Then, the nondominated sorting considering the CDP is performed on the individuals in the set. Unlike the original NSGA-II, here, the crowding distance is defined as the minimum Euclidean distance between a solution and the other solutions regarding the objective space. When two individuals have the same minimum Euclidean distance, the second minimum Euclidean distance is compared, and so forth. In contrast to the original NSGA-II, where multiple individuals with smaller crowding distances are deleted simultaneously, here, individuals with the smallest crowding distance are deleted one by one. After removing an individual with the minimum crowding distance, the crowding distances are recalculated, and then that with the new minimum crowding distance is deleted.

Algorithm 3
figure d

Evolve from feasible side

Full size image

The evolution in the infeasible region

The population evolving in this direction is referred to as the reverse population. The main procedure is depicted in Algorithm 4. In principle, when using the dominance definition that ignores constraints, individuals in the reverse population located on the infeasible side of the CPF are closer to the UPF, as shown in Fig. 3. Therefore, they mostly dominate at least one individual situated on the feasible side of the CPF. In lines 1 and 2, we use this criterion to distinguish the reverse population. The main population P, the previous generation’s reverse population R, the offspring \(O_{fd}\) generated through forward evolution, and the offspring \(O_{rd}\) generated through reverse evolution are combined to form a set. Nondominated solutions from this set are selected, and the infeasible solutions among them are chosen to form the reverse population. Additionally, the CV is introduced as an additional objective in this process, transforming the original problem into an (M+1)-objective UCMOP as

$$\begin{aligned} \min \textbf{F}\left( \textbf{x} \right) =\Bigg ( f_1\left( \textbf{x} \right) ,f_2\left( \textbf{x} \right) ,...,f_M\left( \textbf{x} \right) ,{\text {CV}}\left( \textbf{x} \right) \Bigg ) ^{{T}}. \end{aligned}$$
(4)

The inclusion of CV as an objective aims to select individuals that are closer to the feasible domain. Fig. 3 presents an example. Due to the presence of CV, solutions 3, 7, and 8 are not selected because they are far from the feasible region. Conversely, solutions 3, 7, and 8 are retained because they hold a nondominated position among solutions 1–10. Clearly, we want to retain solutions 1, 2, 4, 5, 6, 9, and 10, which are closer to the CPF.

Fig. 3
figure 3

Illustration of initial screening of reverse population

Full size image
Fig. 4
figure 4

Simple illustration of reverse search

Full size image
Fig. 5
figure 5

Population distribution in the early, middle, and last generation of the second stage on MW9, MW11, and DAS-CMOP5

Full size image

In the early generation of evolution, the size of the reverse population may be smaller than N, and it is not modified. When the size of the reverse population exceeds N, the original problem is considered as its opposite problem, which means that the definition of dominance and constraints become the opposite. From this perspective, the positions of the original infeasible region and feasible region are swapped. If the original problem is a minimization optimization problem, it is now considered a maximization problem, and nondominated sorting is performed on the reverse population. The operation is similar to forward evolution, but the definition of dominance is reversed. Fig. 4 briefly illustrates the reverse search. These operations are presented in lines 6 to 13 in Algorithm 4. The above processes together with the reproduction of the solutions constitute the reverse evolution.

To more intuitively demonstrate the evolution process of the reverse population, Fig. 5 describes the population distributions of BCRS in the early, middle, and last generations of the second stage on MW9, MW11, and DAS-CMOP5. It can be seen that the reverse population was scattered between the CPF and UPF in early generations of the second stage. As the evolution progresses, the reverse population gradually approaches the CPF and exhibits good distribution near the CPF. Finally, the reverse population even visually overlaps with the main population. In general, the reverse population of BCRS can obtain infeasible solutions closer to the CPF through reverse search. It coevolves with the main population and encourages the main population to approach CPF with good distribution and convergence.

Algorithm 4
figure e

Evolve from infeasible side

Full size image

Coevolution and the reproduction of the solution

Inspired by CCMO [12], weak cooperation is used to exchange evolution information between the two directions, meaning that the populations in each direction only exchange individuals among their respective offspring. However, since the reverse population R is closely related to the main population P, the information from P is important for R. Therefore, as shown in line 1 of Algorithm 4, the entire P is included in the cooperation with R.

Since offspring in the two directions can be generated using various different operators. In this paper, we only use the most classic genetic algorithm that employs simulated binary crossover and polynomial mutation to reproduce offspring. This is illustrated in lines 10 to line 13 in Algorithm 1.

Computational complexity of BCRS

The computational time complexity of BCRS depends primarily on its first stage, forward evolution and reverse evolution. In the first stage, BCRS evolves the population P ignoring constraints. Since the MOEA/D is employed in the first stage, the time complexity is \(O(MN^2)\) [35]. In the second stage, the updating of the forward population involves the nondominated sort and the crowding distance sort, which have complexities of \(O(MN^2)\) and max\(\{O(MN^2), O(N^2{\text {log}}_2N)\}\), respectively. The updating of the reverse population involves the discovery of the nondominated infeasible solutions, the nondominated sort and the crowding distance sort, which have complexities of \(O((M+1)N2)\), \(O(MN^2)\) and max\(\{O(MN^2)\), \(O(N^2{\text {log}}_2N )\}\), respectively. As a result, the overall complexity of BCRS is max\(\{O((M+1)N^2), O(N^2{\text {log}}_2N )\}\).

Experimental setup

In this section, a series of experiments is conducted to verify the performance of the proposed BCRS in solving CMOPs:

  • First, the effectiveness of the two-stage and reverse search in BCRS is verified by an ablation study.

  • Then, the proposed algorithm will be compared with nine state-of-the-art CMOEAs including NSGA-II [5], PPS [25], CTAEA [26], CCMO [12], MSCMO [36], CMOEA-MS [37], BiCo [11], MCCMO [33], and MTCMO [13] on four benchmark suites including LIR-CMOP [38], MW [39], DAS-CMOP [40] and CF [41];

  • Next, the multiproblem Wilcoxon test and Friedman test are used to demonstrate the overall performance of BCRS and the other compared algorithms across all 47 problems in four benchmark suites;

  • Finally, BCRS is tested on 15 real-world applications [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57].

Parameter settings

The population size N is set to 100 for each algorithm on each test problem. The number of decision variables D and the number of objectives M of each benchmark suite are set as follows:

  • For LIR-CMOP , M = 3, D = 10 for LIR-CMOP13 to LIR-CMOP14, while M = 2 for other instances;

  • For MW , M = 3, D = 15 for MW4, MW8, MW14, while M = 2 for other instances;

  • For DAS-CMOP , M = 3, D = 10 for DAS-CMOP7 to DAS-CMOP9, while M = 2 for other instances;

  • For CF , M = 2, D = 10 for CF1 to CF7, while M = 3 is set for CF8 to CF10;

All algorithms were independently run 30 times on each test function. For LIR-CMOP, the maximum number of function evaluations (FEs) was set to 300,000. For DAS-CMOP, FEs was set to 200,000. For CF, MW, FEs was set to 100,000. For the real-world problems, FEs was set to 200,000.

For algorithms using the GA operator, the simulated binary crossover (SBX) [58] and polynomial mutation (PM) [59] are used with the following parameter settings. The crossover probability is set to 1, the probability of polynomial mutation is set to 1/D, and the distribution index of both the crossover and the mutation is set to 20, respectively. For the algorithms that adopt DE as the operator, the parameters CR and F in the DE operator are set to 1 and 0.5, respectively. The other parameters of the compared algorithms were held identical with their original papers.

Performance indicators

To evaluate the performance of different algorithms, inverted generational distance (IGD) [60] and hypervolume (HV) [61] are used in this paper as performance indicators:

  • IGD measures the mean distance from the points in the true \(\varvec{P}^*\) to their closest to the solution in the obtained population \(\varvec{P}\):

    $$\begin{aligned} {\text {IGD}}\left( \varvec{P}^*, \varvec{P} \right) =\frac{\sum _{\textbf{x}\in \varvec{P}^*}{{\text {dist}}\left( \textbf{x}, \varvec{P} \right) }}{\left| \varvec{P}^* \right| ,} \end{aligned}$$
    (5)

    where dist\(\left( \textbf{x}, \varvec{P} \right) \) is the Euclidean distance between \(\textbf{x}\) and its nearest neighbor in \(\varvec{P}\). A smaller value of IGD indicates that \(\varvec{P}\) has better performance. In this paper, 10,000 uniformly distributed points are sampled on the true PF for the IGD.

  • HV measures the volume or hypervolume of the objective space enclosed by the obtained solution set and the predefined reference point \(z^r\):

    $$\begin{aligned} HV\left( \varvec{P} \right) =L\left( \bigcup _{\textbf{x}\in \varvec{P}}{\left[ f_1(\textbf{x}), z_{1}^{r} \right] \times \cdots \times \left[ f_M(\textbf{x}), z_{M}^{r} \right] } \right) , \end{aligned}$$
    (6)

    where L denotes the Lebesgue measure. A larger HV value indicates better performance obtained. Note that the calculation of the HV value does not require knowledge of the true PF. To facilitate the computation in the paper, the objective values are normalized, and then \((1.1, 1.1,\cdots , 1.1)\) is adopted as the reference point.

When an algorithm consistently fails to find a feasible solution over 30 runs, the mean IGD and HV values are replaced with “NaN". The Wilcoxon rank sum test at the 0.05 level is presented here to analyze the results, where “\(+\)", “−" and “\(=\)" denote that the result is significantly better, significantly worse, and significantly similar to that obtained by BCRS, respectively. All our experiments are executed on the evolutionary multiobjective optimization platform PlatEMO [62] and run under Windows 10 on i5-8400 CPU with 16 G of memory.

Table 3 IGD values of BCRS-NTS, BCRS-NRS, and BCRS on LIR-CMOP and MW
Full size table

Experimental results and analysis

Ablation study

This part of experiment is designed to validate the effectiveness of the two-stage approach and the reverse search in BCRS. In this study, two variants of BCRS, namely BCRS-NTS and BCRS-NRS, are designed and compared with BCRS on LIRCMOP and MW problems. BCRS-NTS removes the first-stage evolution and BCRS-NRS eliminates the reverse population and the associated evolution operations while keeping other factors the same as in BCRS. Table 3 presents the IGD results of BCRS and its variants, BCRS-NTS and BCRS-NRS, on LIRCMOP and MW problems. BCRS outperformed or performed similarly to BCRS-NTS and BCRS-NRS in almost all the problems. As the results of BCRS-NTS show, it performs more poorly than BCRS in almost all the problems where the CPF coincides with the UPF. This indicates that the strategy of ignoring constraints in the first stage plays a substantial role in BCRS being able to obtain more diverse solutions close to the CPF for such problems. The results from BCRS-NRS indicate that it performs worse than BCRS in cases where the CPF does not coincide with the UPF. Thus, the combined strategy of forward search and reverse search is beneficial for BCRS in addressing problems with considerable feasible and infeasible regions around the CPF.

Experimental results on benchmark suites

Experimental results on LIR-CMOP and MW

The LIR-CMOP test suite consisting of 14 CMOPs, which exhibits small feasible regions, and some of them have only a single curve and are used to test the performance of algorithms in the face of large infeasible regions [38]. MW is another generic test suite that covers diverse characteristics extracted from real-world CMOPs. Feasible regions of MW problems are disconnected, far from the unconstrained PF, or separated by large infeasible regions. All MW test problems have significantly small feasibility ratios [39].

Fig. 6
figure 6

Convergence curves with the IGD obtained by the ten algorithms on the LIR-CMOP9, LIR-CMOP12, MW3, and MW9 test problems

Full size image
Fig. 7
figure 7

Convergence curves with the IGD obtained by the ten algorithms on the DAS-CMOP9, DAS-CMOP12, CF7, and CF10 test problems

Full size image

Tables S-1 and S-2 show the average and standard deviation of IGD values and HV values of NSGA-II, PPS, CTAEA, CCMO, MSCMO, CMOEA-MS, BiCo, MCCMO, and MTCMO on the LIR-CMOP and MW problems for 30 independent runs, respectively. By evaluating the IGD and HV indicators on LIR-CMOPs, we can observe that BCRS achieves competitive results on LIR-CMOP1 to LIR-CMOP4, where the feasible regions are curves. BCRS achieves the best results on LIR-CMOP9 and LIR-CMOP12. For the other LIR-CMOP problems, BCRS performs in the middle range among the ten algorithms. For MW problems, according to IGD values, BCRS exhibits the best overall performance on two MW problems, MW9 and MW11, and competitive results on the other 12 CMOPs. The results are similar for the HV indicator.

Table 4 Multiproblem Wilcoxon test results with respect to IGD and HV on 47 benchmark problems
Full size table
Fig. 8
figure 8

Average rankings of IGD and HV by the Friedman test of BCRS and other algorithms on 47 benchmark problems

Full size image

Figures S-1 and S-2 illustrate the feasible regions of the LIR-CMOP and MW problems in the objective space, respectively. Furthermore, these figures display the final results of BCRS by depicting the positions of its main population in the objective space. The focus here is on the problems for which BCRS obtains best results. Most of these problems have considerable infeasible and feasible regions near their CPFs. For example, in LIR-CMOP12, its feasible regions are relatively narrow and surrounded by a large extent of infeasible regions. Despite this challenging landscape, BCRS still achieves the best results among the ten algorithms. For MW9 and MW11, where there are wide infeasible regions between the CPF and UPF, BCRS achieves the best results. For LIR-CMOP5, LIR-CMOP6, and LIR-CMOP13, the CPF of these problems has no infeasible region, and in second stage, BCRS can only rely on the population of the feasible side to search for the CPF. According to the IGD values, BCRS achieved second or third place on these problems. This indicates that BCRS can achieve competitive results for this type of problem. For the other LIR-CMOP and MW problems, their CPFs mostly coincide with the UPFs, with some parts of the UPFs not belonging to the CPFs. BCRS performs well on these problems. The strategy of ignoring constraints and alternating between the GA and DE strategies in the first stage play important roles in these problems.

To better observe the results, the convergence curves of IGD values of BCRS and other nine algorithms on LIR-CMOP9, LIR-CMOP12, MW3, and MW9 are depicted to demonstrate the performance of BCRS in Fig. 6. Although BCRS is not the fastest, it obtained better indicator results in all instances.

Table 5 Mean (standard deviation) of HV values of BCRS and nine comparison algorithms on real-world problems
Full size table

Experimental results on DAS-CMOP and CF

The CPFs of DAS-CMOP problems are far from the UPFs and CPFs of the DAS-CMOP problems have multiple discontinuous regions except for DAS-CMOP1 and DAS-CMOP2. Tables S-3 and S-4 show the IGD and HV values of BCRS and the nine comparison algorithms on test suite DAS-CMOP. Figure S-3 depicts the feasible region of DAS-CMOP and the final results obtained by BCRS. According to the IGD indicators, BCRS achieves the best performance on two problems: DAS-CMOP2 and DAS-CMOP8. BCRS achieves competitive results on the other problems. Note the difference between DAS-CMOP1-DAS-CMOP2 and DAS-CMOP4-DAS-CMOP5. They have similar feasible regions, but the latter has multiple parallel infeasible regions in the diagonal direction that make the CPF discontinuous. Despite the increased complexity of the feasible regions in DAS-CMOP4-DAS-CMOP5, BCRS achieves better results than on DAS-CMOP1-DAS-CMOP2. This indicates that BCRS is able to guide the solutions toward the feasible region by utilizing infeasible solutions between CPFs. DAS-CMOP3 and DAS-CMOP6 also have feasible regions divided by oblique infeasible regions, and the feasible regions are narrower than those of DAS-CMOP4-DAS-CMOP5. BCRS performs well on these two problems. DAS-CMOP7-DAS-CMOP9 are three-objective problems. Their CPFs are far from the UPF and divided into multiple regions by infeasible regions. BCRS is one of the algorithms that can achieve the best results on these three problems. This suggests that BCRS can effectively utilize the information from infeasible solutions to search for the CPF.

Finally, we also tested ten algorithms on the CF problems, and the results are shown in Tables S-3 and S-4. Figure S-4 presents the graphical results of BCRS on CF problems. The CF test suite represents a case where the feasible regions of the problems are extremely narrow. Some CF problems have only points as feasible regions, while others have curves or a combination of curves and surfaces. Analyzing the IGD and HV values in the two tables reveals that BCRS achieves the best results on CF7, CF8, and CF10 and obtains competitive results on CF3 and CF6. When combined with the good performance of BCRS on LIR-CMOP1-LIR-CMOP4, it demonstrates that BCRC can also achieve competitive performance in problems with curved feasible regions.

The convergence curves of IGD values of BCRS and the other nine algorithms on DAS-CMOP2, DAS-CMOP8, CF7, and CF10 are depicted to demonstrate the performance of BCRS in Fig. 7. Although BCRS might not be the fastest method, it obtained better indicator results.

Statistical results and analysis on all test suites

The experiments are conducted using KEEL software [63]. Table 4 indicates the multiproblem Wilcoxon signed rank test results. All p values are less than 0.05, which indicates a significant difference between BCRS and the other algorithms. Furthermore, all \(R^+\) values are larger than the \(R^-\) values, which indicates that BCRS has significant advantages over other algorithms. The average ranking of all algorithms on all test functions according to the Friedman test is provided in Fig. 8. In the Friedman test, the lower the ranking is, the better the performance of an algorithm. As shown in Fig. 8, BCRS obtains the best ranking in both IGD and HV values. It demonstrates that BCRS exhibits better overall performance than the competitors.

According to the “no free lunch" theorem [64], no algorithm can achieve good results on all kinds of constrained optimization problems. BCRS, compared to the current state-of-the-art algorithms, demonstrates outstanding performance when the problem’s CPF has multiple discontinuous regions with significant infeasible and feasible areas nearby. In other cases, BCRS achieves competitive results. This confirms that BCRS is a competitive algorithm.

Experimental results on real-world applications

In this subsection, we test the performance of BCRS on 15 real-world applications. Table 5 presents the HV values obtained by the ten algorithms. BCRS exhibits the best performance, having obtained five best results, followed by NSGA-II and CMOEA-MS that obtained three best results. MCCMO obtains two best results, PPS and BiCo obtain one best result each, whereas the remaining four algorithms do not obtain any best results. In short, the results indicate that BCRS is also very competitive in solving practical problems.

Conclusions

This paper proposes a CMOEA called BCRS that approaches the CPF from both the feasible and infeasible regions. The algorithm is designed with the intention of fully utilizing the feasible and infeasible solutions on both sides of the CPF to obtain the approximate CPF with good diversity and distribution. BCRS consists of two stages. In the first stage, constraints are ignored, and the population is pushed toward the feasible region while increasing the diversity of solutions. In the second stage, constraints are considered, and the evolution is divided into two parts. The first part focuses on the feasible region, where the main population gradually approaches the CPF within the feasible region. The final solutions are selected from this direction of evolution. The second part treats the original problem as the reverse problem and evolves toward the CPF from the infeasible region. To highlight the synergy between the two directions, a simple variation of NSGA-II-CDP is used for the evolution in both directions. Finally, a weak cooperation mechanism is employed to exchange solutions between the two populations.

During the experimental stage, BCRS was compared with nine state-of-the-art CMOEAs on four benchmarks and 15 real-world problems. BCRS achieved favorable results on most of the problems. Particularly, when the CPF of a problem contains multiple discontinuous regions and has significant infeasible and feasible areas nearby, BCRS performed exceptionally well, thus validating the algorithm’s original intent. Subsequently, through ablation experiments, the effectiveness of reverse search was also confirmed.

In the future, we will focus on balancing the forward and reverse searches to improve the performance of BCRS when the CPF closely overlaps with the UPF. Additionally, we will further research and optimize the methods used to determine the main population and reverse population. In the future, the BCRS can also be improved to solve real-world problems.