Introduction

Problem solving for basic education has become a hotspot research problem again in the recent years because of the confluence of the application demand and the stimulation by artificial intelligence (AI) rapid progress [1, 2], in which solving the arithmetic word problems (AWPs) is the most active research problem. The success of “AlphaGo” further enforces the belief that AI will have the ability to solve the exercise problems in an intelligence way like human being does. Besides being the demand technology of building intelligent tutoring systems, algorithms for solving AWPs are useful technologies in fact-checking tasks to validate the veracity of a given claim [3]. In theory, it is still challenging for AI as it cannot properly solve AWPs yet. Now the problem of solving AWPs is complicated and tricky. On the one hand, it seems not to be a difficult research problem because people and even young kids can often solve AWPs with ease. In another hand, as two recent survey papers have also pointed out, so far there are not many satisfactory solvers after over 60 years of efforts [1, 2]. The theoretical significance, its application demand and its research challenge, motivate our interest in developing algorithms for solving AWPs.

The advances in natural language processing and deep learning now provide a plethora of tools for the development of new algorithms for solving AWPs. Based on these advances, the seq2seq (sequence to sequence) deep neural networks of solving AWPs has been developed in the past years [4,5,6,7,8,9,10,11,12,13]. This seq2seq approach solves the problem using single deep neural networks and gives a final answer without intermediate steps. As a result, it cannot provide the intermediate steps of tutoring students as instructors do.

Except the algorithms in the seq2seq approach, most of the existing algorithms for solving AWPs involve two main steps: problem understanding and symbolic solver. Since the two steps run sequentially, the symbolic solver highly depends on the output of problem understanding. Hence, there has been much effort in developing problem understanding. The methods on problem understanding in the literature can be divided into four main families: semantic analysis [14,15,16,17], rule based [18,19,20,21,22,23], machine learning [24,25,26,27], and syntax-semantics models [28,29,30,31,32,33]. A common shortcoming of these four families of algorithms is that they do not have any component to discover implicit knowledge items for solving AWPs. The existing algorithms have a limited ability in solving AWPs because they do not have any effective methods to acquire such implicit knowledge items. Several studies have been involved the investigation of how implicit relations could be acquired [21, 23, 34], but so far it has not been studied yet how to use both explicit knowledge and implicit knowledge to form the complete knowledge body for solving AWPs. In solving AWPs, the explicit knowledge refers to the quantitative relations stated explicitly in the problem text; the implicit knowledge refers to the knowledge indispensable to solve problems added by the students based on their mastered knowledge. As an example, Fig. 1(b) shows how to add a formula “\(perimeter = 2(length+width)\)” to solve the given AWP, which is an implicit relation from the formula database. Hence, the implicit knowledge in this paper differs from the implicit relation triples produced by the existing relation triples as in [35, 36].

Fig. 1
figure 1

The pipeline of the proposed algorithm and the process that it solves the given AWP. The pipeline of the proposed relation-centric algorithm is in (a); the process that the proposed algorithm solves the given AWP is in (b)

Full size image

This paper proposes a three-phase scheme of developing the algorithm for solving AWPs to decompose the task of developing an algorithm for solving AWPs into three phases, namely creating a state-action paradigm, instantiating the paradigm into a relation-centric approach, and implementing a solving algorithm by adopting the relation-centric approach. The state-action paradigm lies on the recognition that any algorithm of solving AWPs is a loop of the state of knowledge expression and the algorithm action of transforming states. This paper instantiates the state-action paradigm into a relation-centric approach using a group of relations as the intermediate state of the solving process. The proposed algorithm in this paper is a relation-centric algorithm for solving AWPs. The proposed approach is able to provide explainable intermediate steps, being the trait required by the intelligent tutoring systems. Following the existing algorithms, there are two main steps in the proposed algorithm: problem understanding and symbolic solver. Figure 1 shows that the pipeline and a process of solving a sample AWP by the proposed algorithm. Problem understanding is an acquirer that can acquire both explicit relations and implicit relations. The success of this acquirer lies in synergizing a relaxed syntax-semantics (S\(^{2}\)) extractor and a neural network miner. The symbolic solver first forms a group of relations by fusing explicit relations and implicit relations. Then it produces a distilled group of relations by discarding unnecessary relations. Next it transforms the distilled group of relations into a system of equations. The symbolic solver finally outputs the values of the unknown for a given problem by solving the system of equations. The conducted experiments evaluate the proposed algorithm on a collection of nine datasets; the experimental results show that the proposed algorithm outperforms the state-of-the-art algorithms on these datasets. To the best of our knowledge, this is the first algorithm which uses both the extractor for acquiring explicit relations and the neural network miner for mining implicit relations separately to solve more AWPs. In summary, this paper has three contributions as follows:

  1. (1)

    It proposes the three-phase scheme of building algorithms for solving AWPs, which consists of building a state-action paradigm, instantiating a relation-centric approach, and implementing a relation-centric algorithm.

  2. (2)

    It proposes the first relation-centric algorithm that can solve both explicit AWPs and implicit AWPs.

  3. (3)

    It creates an acquirer that synergizes a relaxed S\(^{2}\) extractor of acquiring explicit relations and a neural network miner of mining implicit relations.

In the rest of the paper, “Related work” first provides a review of the related work. “State-action paradigm and relation-centric approach” then builds the state-action algorithm paradigm and the relation-centric approach. “A relation-centric algorithm for solving AWPs” presents the proposed algorithm for solving AWPs. “Experiments” presents the algorithm analysis and experimental results. “Conclusions and future work” concludes the paper.

Related work

This section starts with reviewing the solving approaches of the existing algorithms because there is no related work in building the solving algorithm paradigm yet. The existing algorithms for solving AWPs are divided into five approaches according to the different expression forms of the understood state of AWPs. The algorithm proposed in this paper consists in two phases of problem understanding and symbolic solver. Hence, the related work is also about problem understanding and symbolic solver.

The related work in solving approach

Researchers have proposed many algorithms to solve AWPs. Through analyzing the process of solving problems, one can form the following conclusion: solving problems is to present the knowledge in different states and to use actions to transform knowledge expression from a state to another state. For example, some algorithms use a system of equations as the main intermediate state of AWPs. Their main actions are to build the system and solve the system. Then, this paper proposes to mainly use the knowledge expression forms of the main states to define the approaches of solving algorithms. According to these forms, the existing algorithms can be divided into five approaches: (1) two-frame, (2) equation-centric, (3) answer expression, (4) seq2seq, and (5) relation-centric. The concepts and methods of the five approaches will be the base to build the state-action paradigm proposed in this paper. We review the five approaches as follows.

  1. (1)

    Two-frame: Back in 1985, Kintsch et al. [14] proposed a two-frame approach to solve AWPs. This approach uses two types of frames to store the outcome of problem understanding, namely knowledge frames and solution frames. This approach addressed the representation of outcome of problem understanding and the scheme of knowledge inference. It uses the knowledge frames to store the extracted knowledge items by problem understanding; the solution frames to store the inference schemes. It uses sentence templates to extract knowledge from problem text in order to fill abstract knowledge frames. Subsequently, the researchers proposed semantic sentence templates and deep neural networks to extract knowledge items from problem text [11, 15,16,17]. However, the two-frame approach suffers from a couple of limitations. The first one is that the number of sentence templates can become quickly large due to the large variety of expressions for a given semantic meaning. The other one is that there is no uniform way to infer knowledge frames according to solution frames.

  2. (2)

    Equation-centric: Equation-centric approach is to solve AWPs with methods around equations. Since the mathematical tools can solve the system of equations, the main phase of this approach is problem understanding, i.e., how to form such a system of equations. Hence, many papers studied various methods to form system of equations. Some methods acquire equations one by one [18, 37,38,39,40,41]. Some other methods acquire all equations using equations templates. Kushman et al. [24] first proposed machine learning (ML) method to acquire all the equations together. The ML method prepares a pool of equations templates. The trained ML finds out which template is suitable for the given problem followed by matching entities with elements of the equation template. The ML methods was further studied in [25,26,27, 42]. However, both ways have the limitation of acquiring the proper group of equations. The way of acquiring equations one by one, encounters the difficulty in assigning the same variable to the same entity because the same entity may have different appearances in different equations. The way of acquiring equations using equations templates, encounters difficulty in building a pool of equation templates that can achieve high problem accuracy. Another demerit of the equation-centric approach is that most of the algorithms in this approach have a limited scope because they can produce only linear equations [18, 24,25,26,27, 37, 38, 41, 42].

  3. (3)

    Answer Expression: The approach of answer expression is to solve the problem by forming the answer expression from the extracted knowledge items. An answer expression is an expression of numbers and operands; the answer is the result of evaluating this expression with the assumption that a problem requires a single answer. The algorithms in this approach used various methods to extract knowledge items and form the answer expression. Roy et al. [20] first proposed to use quantity schema and multiple classifiers to map problem text to answer expression. Subsequently, some researchers proposed to use unit dependency graph [21], formula templates [22], or declarative rules [23] to extract knowledge items for forming answer expressions. In the recent years, some researchers proposed to use deep reinforcement learning [43] or deep neural networks [44, 45] to form answer expressions. Answer expression is an indispensable state of this approach and the methods to extract knowledge items and form this expression are the corresponding actions. However, such actions cross a big span from input to answer expression so they are complicated. Thus, answer expression carries two drawbacks: (i) it can only solve single unknown problems so far; (ii) it can hardly explain the internal reason or inference of the expression generation.

  4. (4)

    Seq2Seq: The seq2seq approach is to solve the problem using the trained machine to obtain the sequence of answer expression, which assumes that a problem requires a single answer so far. This approach is different from the approach of answer expression lying in that it mainly computes vectors, although both approaches target to acquire answer expressions. It first converts problem text into vector sequence and then uses the trained machine to accomplish a transformation from vector sequence of problem text into vector sequence of answer expression. Some papers call this approach as data-driven approach because this approach needs data to train learning machines [46, 47]. Wang et al. [4] first proposed a seq2seq approach to design algorithms for solving AWPs. Subsequently, researchers proposed more deep neural networks to translate problem text into answer expression [5,6,7,8,9,10, 12, 13, 48]. The seq2seq approach suffers a demerit that the actions taken by deep neural networks are not explainable.

  5. (5)

    Relation-centric: After learning from the above-listed four approaches, Yu et al. [28] proposed a relation-centric approach to solve AWPs and proposed to use S\(^{2}\) method to extract relations from problem text. More researchers paid attention to this approach because it has multiple merits. First, it inherits the merit that the actions are explainable to students because it adopts model-based method. Second, it also demonstrates the advantage of equations because it is easy to convert relations into equations. Third, acquiring relations is easier than acquiring equations. Acquiring equations one by one by S\(^{2}\) method proves to be a much easier task than directly acquiring a batch of equations. The relation-centric approach was successfully applied in understanding plane geometry problems and direct current circuit problems [31,32,33], but it has a limited performance when solving AWPs as it cannot acquire implicit relations yet [29], which we have tried to tackle further in this paper.

In a word, this paper adopts the relation-centric approach to develop an algorithm that can broaden the range of solving arithmetic word problems and output explainable solutions that can provide tutoring service to students. Such an algorithm is also applicable to fact-checking task, which validates the veracity of a given claim [3], because it can output an algorithmic solution and a series of algorithmic actions from one state to another. In contrast, the algorithms of adopting some other approaches, especially seq2seq, do not have such ability because they cannot give understandable intermediate results.

The related work in problem understanding

There are four main methods for problem understanding: template matching, rule searching, machine learning, and S\(^{2}\) model.

The method of template matching uses a pool of templates to extract knowledge items from problem text [14]. A large number of templates are needed because templates are semantic [15]. The rule searching is to search and identify the various scenarios to produce equations. This method also needs a large number of rules because there are many different scenarios [18, 23]. The machine learning method leverages the designed features to search the most probable equation template [24, 25, 27]. This method can hardly explain the internal reason of the equation template selection. Researchers proposed the S\(^{2}\) model method to work against the variety of semantics and scenarios [28, 29]. The S\(^{2}\) model method has overcome the dimension disaster of semantic expressions by increasing the use of syntax patterns and reducing the use of semantic patterns. However, these four methods mainly extract the explicit relations, though they can acquire some implicit relations. Hence, this paper develops a method to acquire more implicit relations.

Here we review the methods involving in acquiring implicit relations. In 2016, two studies attempted to address the problem of implicit relation acquisition. The first study, done in Mitra et al. [22], relies on a machine learning method to find equations for three mathematical situations, i.e., 1) part whole, 2) quantity change, and 3) quantity comparison. Among these three situations, only the first one refers to a type of implicit relations as problem text normally does not explicitly state the relation of part whole. The second study, done in Yu et al. [49], focuses on adding an additional formula into outcome of problem understanding. Such a formula corresponds to an implicit relation, as it essentially is a knowledge point requiring students to add an appropriate formula when they are solving problems. To test how well students master this knowledge point, problem text should not explicitly state it. However, problem text expressions will often provide hints of adding the required formula. Based on this fact, Yu et al. [49] proposed an SVM based method to find additional formulas to be used in solving AWPs. The proposed method is not cutting-edge because it relies on bag-of-words rather than vector features. In another study, Dewappriya et al. [34] proposed an ontology-based unit system to resolve unit conflicts. The system mainly aimed at preventing unit conflict before running the main portion of solving algorithm and thus acted as a preprocessing step.

Learning from the existing methods, this study proposes an algorithm for solving AWPs. The algorithm uses a relaxed S\(^{2}\) method to extract explicit relations and a neural network to acquire implicit relations. More specifically, the proposed algorithm relies on a BERT based neural network to find implicit relations. The phase of problem understanding thus essentially changes to acquiring a group of relations while the symbolic solver conducts an equivalent transform of relations. This is the first algorithm that can solve a large number of AWPs involving both explicit and implicit relations.

The related work in symbolic solver

Researchers put less effort in developing symbolic solvers because it is not difficult to solve the outcome of problem understanding in most cases. For the algorithms of adopting the equation-centric approach, the outputs of their problem understanding are systems of linear equations [18, 24,25,26,27, 37, 38, 41, 42]. Hence, their symbolic solvers are somewhat simplistic because Gaussian elimination can solve such systems. For the algorithms of adopting the approach of answer expression, the outputs of their problem understanding are in various formats of arithmetic expressions so that they do not need any complex symbolic solver [20,21,22,23, 43,44,45]. The algorithms adopting approach of two-frame used the heuristic ways to find answers [11, 14,15,16,17]. The algorithms of adopting the relation-centric approach have a decent symbolic solver [28, 30, 32]. The reason is that the equations produced from relations might not be linear. Hence, Yu et al. [29] proposed a method leveraged on the idea of recursively solving the linear portion of all equations. This paper will continue to use this method to build the symbolic solver.

Fig. 2
figure 2

The state-action paradigm of solving AWPs

Full size image

State-action paradigm and relation-centric approach

This paper proposes a three-phase scheme to develop algorithms for solving AWPs, which is a scheme to design algorithms from abstract to concreteness. This section presents the first two phases. The first phase is to design a solving paradigm. Concretely, it proposes a state-action paradigm for solving AWPs as solving paradigm. The second phase is to define the states of the state-action paradigm to form a relation-centric approach to solving AWPs.

The goal of this paper is to design high performance algorithms for solving AWPs. Through analyzing the algorithms in the literature, the loop of states and actions can explain the process of solving AWPs by algorithms. Hence, this paper proposes a state-action paradigm as depicted in Fig. 2 and uses it as the algorithm paradigm of solving AWPs. In this paradigm, the states are different states of knowledge expression and actions are the algorithm actions to transform from a state to another. This abstract solving paradigm is a simple diagram, but it can guide us to understand what the solving algorithms are doing and what the core issues of solving problems are. It also can explain how we design approaches and algorithms for solving AWPs. More importantly, the approach of solving AWPs can be defined based on the abstract solving paradigm.

Definition 1

(Approach) An approach is an instance of the state-action paradigm by determining the main states of the state-action paradigm and the links to change from a state to another.

“The related work in solving approach” has classified the existing algorithms in the literature into five approaches. We take two approaches as examples to show that all the five approaches conform to Definition 1. The first approach is seq2seq. The algorithms in this approach have two related states: a vector sequence and the sequence of answer expression. Thus, they have three common links. The first link is the encoding step to encode the given problem into a vector sequence. The second link is to transform a vector sequence of problem text into a vector sequence of answer expression. The third link is to evaluate answer expression and output the answer. The second approach is relation-centric. The algorithms in this approach have one common state, which is a group of relations. Thus, they have two common links. The first link is to acquiring a group of relations, being another kind of problem understanding. The second link is to solve the group of relations.

Building a link from one state to another means that researchers have found methods to accomplish this state transformation at least for a corpus of problems. Along this state-action solving paradigm, designing algorithms means to propose methods to implement the links of the adopted approach.

All the states in the state-action solving paradigm are the states equivalent to the given problem in terms of solving AWPs. Among these states, researchers want to acquire an understood state, which is defined as follows.

Definition 2

(Understood State) A state is called an understood state of a given AWP if a symbolic solver can produce the solution from this state without revisiting the given problem.

From Definition 2, all the states except the input state and the vector sequence of problem text in the five approaches are understood states.

Definition 3

(Problem Understanding) Problem understanding is to produce an understood state of AWPs.

Definition 4

(Relation) A relation is an equation expression of quantifiable entity, where a quantifiable entity can be a number, a variable, or a phrase that describes a quantity.

A relation differs from an equation in that its items may be phrases except variables and numbers. In this paper, a relation is actually a quantity relation because all its elements are about quantity.

Proposition 1

Assume that \(\mathcal {C}\) is a corpus of AWPs. Let \(\mathcal {P}\) be an AWP in \(\mathcal {C}\). Then there is a group of relations denoted as Œ\(= \{r_{i}:\;i=1\;to\;k\}\) such that it is an understood state of \(\mathcal {P}\).

A theoretical proof for Proposition 1 is not available so far, but the experimental results in “Experiments” will testify its correctness. Actually, Proposition 1 is the assumption of many existing algorithms for solving AWPs.

We define the relation-centric approach formally because it is a central term of this paper.

Definition 5

(Relation-Centric Approach) A relation-centric approach is an instance of the state-action paradigm such that: 1) it has two links of problem understanding and symbolic solver; 2) the link of problem understanding is to produce a group of relations that is an understood state of a problem; 3) the link of the symbolic solver is to find values of the unknowns in the given problem through transforming the group of relations.

Definition 5 shows that relation acquisition and relation transformation are the main operations of the relation-centric approach. This approach benefit from the fact that relation extraction from text is more tractable than equation extraction.

A relation-centric algorithm for solving AWPs

This section presents a relation-centric algorithm for solving AWPs by implementing the relation-centric approach.

Algorithm outline

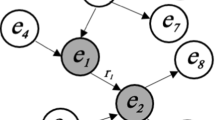
This section instantiates the relation-centric approach into a three-step algorithm to solve AWPs. The first step is to acquire a group of relations. The second step is a symbolic solver, which solves the group of relations. The last step is to output the unknowns with found values and an algorithmic solution, which is a series of actions of acquiring and transforming relations, recorded along the algorithm execution. These three steps constitute the proposed algorithm, which is shown in Algorithm I. The proposed algorithm uses five procedures, namely Procedure I to V, to implement the five tasks of the algorithm. The process of solving problems by Algorithm I is explainable because people can understand all the actions of acquiring and transforming relations. More importantly, this series of actions can instruct students how the algorithm solves the problem. Figure 1(b) shows the process that Algorithm I solves a given AWP to demonstrate how Algorithm I works.

figure a

Acquiring relations of AWPs

This section presents the method details of acquiring relations from AWPs. It comprises two aspects: (1) extracting explicit relations, and (2) acquiring implicit relations.

Definition 6

(Explicit and Implicit Relation) Let \(\mathbb {R}\) be a set of relations that is an understood state of a given AWP. A relation in \(\mathbb {R}\) is an explicit relation if it explicitly states in problem text; otherwise, it is an implicit relation.

Extracting explicit relations using relaxed S\(^{2}\) method

This section designs a relaxed S\(^{2}\) method by enhancing the S\(^{2}\) method. Compared with the original S\(^{2}\) method, the relaxed S\(^{2}\) method relaxes the requirement that each piece of text can match only one S\(^{2}\) model and delays the action of judging whether an extracted relation is used by the coming symbolic solver. Procedure I uses the proposed relaxed S\(^{2}\) method to extract explicit relations. The syntax portions of S\(^{2}\) models are comprised of patterns of POS (part-of-speech) and punctuation while the semantic portions are keyword structures. Procedure I can work only after a pool of S\(^{2}\) models are prepared appropriately for a natural language.

Fig. 3
figure 3

The process of using S\(^{2}\) method to extract explicit relations from a sample AWP

Full size image
figure b

Definition 7

(S\(^{2}\) Model) A syntax-semantics model, shorted as S\(^{2}\) model, is defined as a quadruple \(M = (K,\,P,\, Q;\, R)\), where K represents semantics keyword structures, P represents POS, Q represents the punctuation, and R is the relation as model output. Let \(\Sigma = \{ M_{i} = (K_{i},\, P_{i},\, Q_{i};\, R_{i})\;\vert i =1,2,...,m\}\) denote the set of all the prepared S\(^{2}\) models, called as a pool of S\(^{2}\) models for AWPs.

Definition 8

(Matching Action) A matching action is an action which matches the structure of \(K,\, P,\, Q\) from a quadruple \(M = (K,\, P,\, Q;\, R)\) to a portion of problem text.

After loaded with a pool of S\(^{2}\) models, Procedure I can extract explicit relations from a given input text. To acquire all explicit relations, it is necessary to match all the models in the pool with all potential portions of text. The crucial point of the procedure is to judge whether a model matches a portion of problem text. The outcome of this procedure is a set of explicit relations. Figure 3 uses an example to illustrate how Procedure I extracts explicit relations from AWPs. This whole process is called as an S\(^{2}\) method.

Table 1 The list of eight frequently used models from the pool of S\(^{2}\) models for solving AWPs in English and examples of these eight models extracting explicit relations from problem text
Full size table

When using the S\(^{2}\) method, the main job of model matching is to match the POS change pattern with a portion of text. There are eight types of frequently used POS in S\(^{2}\) models in English: n (nouns), v (verbs), a (adjectives), p (pronouns), m (numerals), c (conjunctions), r (particles), and w (punctuation marks). Each POS type corresponds to one of the twelve universal POS tags from natural languages.

This paper prepares pools of S\(^{2}\) models for Chinese and English respectively. The pools of S\(^{2}\) models for Chinese and for English consists of 220 and 360 S\(^{2}\) models respectively. Table 1 lists eight frequently used S\(^{2}\) models for solving problems in English.

Neural network miner for acquiring implicit relations

This section develops a procedure to acquire the implicit relations from problems. There are two cases of the implicit relations considered in this paper: unit conversion and arithmetic formula. Unit conversion is to add the relations that convert the different units of the same measurement appearing in the same problem. Arithmetic formula targets to add appropriate formula about corresponding scenarios. For example, when a problem appears to a scenario of calculating the area of a rectangular object, the component adds the formula of the rectangle area.

For the unit conversion, Dewappriya et al. [34] considered it as an issue of unit conflict and proposed a procedure to solve it. This paper adopts this procedure and uses it as a prior process to obtain the entire unit conversion relations for each measurement system involved in a given problem without giving the detail of this process.

For the arithmetic formula, the neural network miner can be a useful tool for such types of tasks since it can acquire the hints from the problem text. As it is known, the implicit relation belonging to the arithmetic scenario is highly related with quantity words. Hence, this paper proposes a neural network miner based on quantity to relation attention neural network (QRAN) to mine implicit relations (Procedure II). The procedure consists of three steps:

figure c

The first step is to encode the given problem into a sequence of vectors. A given problem can be tokenized as \(\mathcal {P}=\{w_{i}\}_{i=1}^{n}\), each token \(w_{i}\) can be represented as a word-context feature vector \(v_{i}\) by BERT [50]. Thus, \(\mathcal {P}\) can be denoted by a sequence of vectors as \(\mathcal {V}=\{v_{i}\}_{i=1}^{n}\). The next process is to select the vectors related to quantity, including the numeric words like “100”, “1/2” and the descriptive words like “double”, “half”. Let \(\mathcal {N}\) denote the set of the quantity vectors in the problem, and place \(v_{i}\) into \(\mathcal {N}\) if \(w_{i}\) is a quantity word. Thus, \(\mathcal {N}= \{ q_{i}\}_{i=1}^{k}\) contains all the quantity vectors, where k is the total number of the quantity words in a problem.

The second step is to obtain the goal vector \(v_{g}\) representing implicit relations by adopting the quantity-relation attention mechanism. The concrete computing process is as follows:

$$\begin{aligned}&{\mu }_{i}=\alpha \cdot tanh(W_{r} \cdot [\bar{v},q_{i}] )\; \quad for\;i=1,2,...,k. \end{aligned}$$
(1)
$$\begin{aligned}&{a}_{i}=\frac{exp({\mu }_{i})}{\sum \nolimits _{j=1}^{k} exp({\mu }_{j})} \end{aligned}$$
(2)
$$\begin{aligned}&v_{g}=\mathop {\sum }\limits _{i=1}^{k}{a}_{i}\cdot q_{i} \end{aligned}$$
(3)

where \({\bar{v}}\) is the average vector of the sequence \(\mathcal {V}\), \({\mu }_{i}\) is the relevance score between the whole problem and a quantity related word, \({a}_{i}\) is the attention score of each quantity in a softmax manner, \(\alpha \) and \(W_{r}\) are parameters trained for each specific implicit mathematical relation.

The goal vector \(v_{g}\) can be transformed to a indicator \(\hat{y}\) through a dense layer, judging whether an implicit relation needs to be added. The \(\hat{y}\) is defined as Eq. (4). As \(\hat{y}\) is the predicted value of the implicit relation category, we can get the corresponding relation from the prepared implicit relation knowledge base.

$$\begin{aligned} \hat{y} = \sigma (W_{c} \cdot v_{g} + {\beta }_{c}) \end{aligned}$$
(4)

where \(\sigma \) is the sigmoid function, \(W_{c}\) and \({\beta }_{c}\) are trainable parameters.

A knowledge base \(\mathbb {D}\) consisting of pairs of implicit category with a corresponding formula (abstract relation) is constructed. We assume that the ground truth label of a problem is \(y \in {\mathbb {D}}^{C}\), where \(y_{i} = \{0, 1\}\) denotes whether label i appears in the problem or not. The whole network is trained using the multi-label classification loss as follow

$$\begin{aligned} Loss(y,\hat{y}) = -\frac{1}{C}\mathop {\sum }\limits _{i=1}^{C}[y_{i}log(\hat{y_{i}})+(1-y_{i})log(1-\hat{y_{i}})] \end{aligned}$$
(5)

where C denotes the number of categories of formula (implicit relations).

Fig. 4
figure 4

The architecture of the main part of Procedure II

Full size image

The third step is to instantiate the variables in the formula by connecting the entities in problem text. Each variable in implicit relation are transformed to word vectors through BERT, represented as a vector \({I_{i}}\). And each entity in the problem text obtained in extraction of explicit relation can be represented as a word vector \(E_{j}\) = \(\bar{\{{v}\}}^{l}\), where l is the token length of the word. The cosine similarity \({cos(I_i, E_j)}\) is adopted to calculate the semantic similarity between variable in implicit relation and the entity in text. Once the similarity \({cos(I_i, E_j)}\) get the max value, the i-th variable in abstract relation would be substituted by the j-th entity in problem text. A instantiated implicit relation would be obtained after all the variables connecting to the corresponding entity. For a problem, all the instantiated implicit relations would be added to the output collection \(\Delta \) finally.

Procedure II adds implicit relations to complement the problem understanding relying on the trained QRAN to discover the requiring abstract relations. Figure 4 illustrates an architecture of the main part of Procedure II. The implementation details of QRAN are presented in Appendix A.

Symbolic solver

Symbolic solver takes three steps to transform the group of relations to find the values of unknowns. The first step is to acquire the group of distilled relations (Procedure III). The second step is to build a system of equations (Procedure IV) and the third step solves the system of equations (Procedure V).

Distillation of explicit and implicit relations

Procedure I and II together produce a set of candidate relations from a given problem text. These candidate relations might contain relations that symbolic solver does not use and they might lead the solver to produce wrong results. Hence, a procedure needs to discard as many as possible these unnecessary relations. Procedure III proposes to perform the selection from the set of candidate relations based on global and connection characteristics. The main idea lies in identifying the necessary relations according to their link with problem unknowns. The detailed process is as follows: First, it builds a relation graph, whose nodes are all the candidate relations and whose links indicate whether two relations are relevant. We start to build this graph from the relations that contain the unknowns; add a node for a relation and add links if it has the sharing quantity objects with the built nodes in the graph and it is consistent with nodes in terms of arithmetic formulas. In other words, whether two relations are relevant is equivalent to whether two relations have the sharing quantity objects and they are involved in the same arithmetic formula. Then it identifies the solution graph, which is a partial graph, contains all problem unknowns and all nodes connecting to any unknown, and all the links among these nodes. The relations in the solution graph forms a set of distilled relations.

figure d

Forming a system of equations

To obtain the system of equations for a given problem, we need to list all entities that appear in the distilled relations. Then we assign a variable to each entity. The assigned variables replace all the entities in the distilled relations. Each relation thus turns into an equation and all the relations form a system of equations. The system of equations and the entity-variable table represent the given problem together. The detailed process is given in Procedure IV.

figure e
figure f

Solving the equation system

The system of equations always contain some linear equations, though the whole system may not be a linear system. Gaussian elimination can solve these linear equations. The new linear equations forms when the solution of the linear equations replaces variables. This recurring manner will solve the whole system of equations. The detailed process is shown in Procedure V.

Experiments

This paper prepares nine datasets from authoritative resources and chooses five baseline algorithms as benchmarks. Then it compares the proposed algorithm with the five baseline algorithms on the nine datasets.

Experimental settings

Datasets: An explicit AWP is an AWP such that a group of explicit relations is its understood state; an implicit AWP is an AWP that is not explicit. Thus, each of the datasets can be divided into an explicit set and an implicit set; the explicit set (the implicit set) contains all the explicit problems (the implicit problems). Assume that X is the name of a dataset. Then X:E, X:I and X:3 denote three partial sets of X. X:E denotes the explicit set of X that contains only explicit problems; X:I denotes the implicit set of X that contains only implicit problems; X:3 denotes the special set of X that contains problems whose equivalent relation group needs at least one relation of part whole, time distance, and interest. Table 2 gives a list of sample problems corresponding to the three partial sets X:E, X:I, and X:3. In addition, each dataset has its English and Chinese versions, no matter the language in which its original version is.

Table 2 The list of sample problems corresponding to the three partial sets X:E, X:I, and X:3
Full size table

Table 3 lists the prepared nine datasets: PEP, BNU, and USC are three datasets from textbooks, which include all problems from textbooks for primary students published by People’s Education Press in 2018, by Beijing Normal University in 2018 both in China, and used in California of USA in 2018, respectively. EEP is a dataset that includes all problems from entrance exam papers for high school in 34 provinces of China from 2010 to 2019. M23K, Ape5kT, MAWPS, Dol2K, and Arith are five datasets of AWPs from the generic research community. Math23K is a popular dataset in Chinese. Ape210K is currently the largest dataset in Chinese. M23K is from Math23K by discarding pure numerical problems and special symbol calculation because both baseline algorithms and the proposed algorithm are not designed for such problems. Ape5kT is the test set of Ape210K, which is the test portion of Ape210K in [9]. The baseline algorithm in [9] was tested on Ape5kT, after it used Ape210K as training set. Hence, Ape5kT is chosen as test set instead of Ape210K because the existing algorithms have never been tested on Ape210K. MAWPS, Dol2K, and Arith are another three test datasets used by the baseline algorithms.

Table 3 The prepared nine datasets and their sources
Full size table

Baseline algorithms: The algorithm presented in this paper is denoted as PROPOSED in this section. This paper compares PROPOSED with five baseline algorithms described below. PROPOSED fully compares with the first four of five baseline algorithms on the nine datasets because their implementations are provided by the authors of the papers or prepared by us.

  • MaAlg: MaAlg is an algorithm presented in [15], being the best one among the algorithms of adopting two-frame approach. It improved Kintsch’s algorithm presented in [14] in two aspects. First, the algorithm extends the definition of knowledge frame so that it can solve problems that require multiple steps. Second, it uses more than 1600 sentence templates to extract knowledge from problem text.

  • RoyAlg: Roy et al. [20] proposed an answer expression approach that lies in mapping obtained quantities and operands to an expression. RoyAlg is reported in [23], being a representative algorithm among the multiple algorithms in this approach [20,21,22,23].

  • ZhaoAlg: ZhaoAlg is a seq2seq algorithm proposed in [9]. ZhaoAlg leverages on an open Neural Machine Translation (NMT) tool with a copying mechanism. The largest dataset of AWPs is used to train NMT, however, the trained network is tested only on Ape5kT.

  • LinAlg: LinAlg is another seq2seq algorithm in [12]. It uses a hierarchical structure to enhance the ability to understand math word problems. Unlike the previous seq2seq model that encodes the text into a single vector sequence for decoding [4, 7, 8, 10], this model uses a hierarchical coding structure to encode the contextual semantics of the words in the clauses, the semantic dependencies in the clauses, and the inter-clause relation, respectively. The decoder decodes the vector sequences formed in different levels of hierarchy to enhance the decoder’s attention to different levels of semantic information.

  • ShiAlg: ShiAlg is an equation-centric algorithm in [18] and uses the formal language as its intermediate form. The design of this algorithm requires DOL (abbreviation of dolphin language) as an intermediate language. Given a problem, the algorithm first converts it into its intermediate expression in DOL. Then it derives a system of equations from the DOL expression of problems.

Mandal et al. [44] proposed an another answer expression algorithm. It uses a BiLSTM to classify operations among four basic operations and an irrelevant-information removal unit to identify the relevant quantities to form an expression to solve AWPs. It conducts experiment on AddSub and SingleOp, being two subsets of MAWPS, where all the problems only require a single equation with a single operation to be solved. This paper does not select the algorithm presented in [44] as a baseline because it targets to solve a limited scope of AWPs.

The implementation of the baseline algorithms: This study implements MaAlg, ZhaoAlg, and LinAlg algorithms on our own test platform. Since both ZhaoAlg [9] and LinAlg [12] algorithms are a deep learning model, we set the same parameters as their original papers respectively. For RoyAlg, this study uses the source code provided by [23], taking problems in English as its input. Hence, RoyAlg can run on all the English datasets.

Experimental results

An arithmetic word problem (AWP) is an arithmetic exercise problem in the primary mathematics described in natural language. An algorithm is said that it can solve an AWP if it can output the correct pairs of all the unknowns of the problem and their values after a series of correct transforms.

An algorithm also called as a solver of AWPs if it can solve a decent percentage of AWPs from a dataset.

This paper compares PROPOSED with the baseline algorithms mainly using two evaluation indicators: (i) The first indicator is the correct accuracy, which is the percentage that an algorithm can correctly solve the AWPs from a dataset. So far the most solving algorithms have mainly focused on generating the correct answer and adopted the correct accuracy as the main evaluation indicator. (ii) The second indicator is the number of models and the corresponding correct accuracy. Both MaAlg and ShiAlg use a pool of templates or rules. The number of models or templates is a key indicator when evaluating these algorithms. Hence, PROPOSED also compares with MaAlg and ShiAlg on the number of templates or models because only these two baseline algorithms use templates or models to extract the knowledge from problem text.

PROPOSED compares with the baseline algorithms on the accuracy of solving problems in three cases for each of datasets: (i) on whole dataset; (ii) on explicit problems only; and (iii) on implicit problems only.

PROPOSED emphasizes on its application to learning systems. Hence, it outputs not only the answers of unknowns but also the understandable algorithmic solution. It shows that PROPOSED can output the understandable algorithmic solution that can explain to students how to solve the given AWPs used an example in Fig. 1(b).

Table 4 The analytical comparison on the accuracy of solving problems considering PROPOSED against the four baseline algorithms on the nine datasets
Full size table

Table 4 displays the analytical comparison of accuracy of solving problems between PROPOSED and the four baseline algorithms, namely MaAlg, RoyAlg, ZhaoAlg, and LinAlg, on the nine datasets. The analytical comparison is to find out the performances of the involved algorithms on explicit problems, implicit problems and problems with three types of relations. PROPOSED is tested on both Chinese and English version of every dataset whereas a baseline algorithm is tested on Chinese (English) version of every dataset as it actually did in the reference paper.

In Tables 4 and 5, “–” indicates that the corresponding item is not available; a number in “Size” column/row indicates the number of the problems in the corresponding dataset; a number in “%” column indicates that the percent of problems that the corresponding algorithm can solve on the involved dataset. Table 4 reveals the four important conclusions:

  • First, the component of acquiring implicit relations plays a critical role in enhancing the accuracy of PROPOSED. In accuracy, PROPOSED is at least 6.5% higher than any of four baseline algorithms on the nine datasets. PROPOSED achieves an accuracy of 78.3% on the Chinese version of the union of the nine datasets, whereas LinAlg achieves an accuracy of 71.8%, being the highest accuracy among the four baseline algorithms.

  • Second, PROPOSED has a much better performance in solving implicit problems than the baseline algorithms. It is at least 18.2% higher than any of baseline algorithms on all the implicit subsets of the nine datasets. PROPOSED achieves an accuracy of 81.9% on the union of the Chinese implicit subsets of the nine datasets, whereas LinAlg achieves an accuracy of 63.7%, being the highest accuracy among the four baseline algorithms. On the set of all Chinese implicit problems with three types of relations of the nine datasets, PROPOSED is still at least 13.7% higher than any of baseline algorithms is.

  • Third, PROPOSED has a better performance in solving problems on any particular dataset that even favors the particular algorithm. For example, Arith favors RoyAlg because problems in Arith have only types of the implicit relations discussed by RoyAlg. Hence, RoyAlg achieves an accuracy of 85.5%, being the highest percent among the nine datasets. Even so, PROPOSED is 2.8% higher than RoyAlg on the same dataset in accuracy of solving problems, which achieves an accuracy of 88.3%.

  • Fourth, PROPOSED is just slightly better than LinAlg on the Chinese explicit problems of the nine datasets. Specifically, PROPOSED is 77.3% and LinAlg 74.0% for this accuracy. This can be partially explained by the fact that PROPOSED is even 0.1% lower than LinAlg in solving the problems in M23K:E, being one of nine explicit datasets.

Table 5 The comparison on the accuracy of solving AWPs and the number of models considering PROPOSED against both MaAlg and ShiAlg on the explicit portions of the nine datasets and Dol2K dataset respectively
Full size table

Among the five baseline algorithms, Ma et al. [15] has listed the sentence templates so that this study implements it on our test platform. Hence, PROPOSED can compare with MaAlg on solving explicit problems because the sentence templates can extract only explicit relations. MaAlg claims that it has correctly understood a problem if the frames filled by MaAlg contain all knowledge items needed by symbolic solver, while PROPOSED can understand a problem if it can acquire a group of relations as an understood state. Table 5 shows two parts of comparisons. The first part is that PROPOSED compares with MaAlg on Chinese versions of the nine datasets. The other part is that PROPOSED compares with ShiAlg on English versions of Dol2K dataset. We only implements MaAlg whereas the numbers on ShiAlg in Table 5 are cited from [18].

Table 6 The ablation experiments on the nine datasets of showing the contribution of the relaxed S\(^{2}\) method and QRAN to the accuracy of PROPOSED solving AWPs
Full size table

In Table 5, “1600+m” and “220m” mean that the corresponding algorithms use more than 1600 and 220 models respectively. Table 5 mainly presents the accuracy of solving problems on datasets with the number of used models. The accuracy is in the format of X%. For example, the first accuracy 79.2% means that MaAlg achieves 79.2% when it uses 1600+ models to work on PEP:E dataset in Chinese. Table 5 shows that PROPOSED is 4.9% higher than MaAlg on the accuracy on PEP:E in Chinese under the condition that the number of S\(^{2}\) models used in PROPOSED is only one seventh of the number of sentence templates used in MaAlg. PROPOSED needs a smaller number of models because its models use syntax as much as possible, thus overcoming the variety of semantic expressions. Table 5 also shows that PROPOSED is much better than ShiAlg in both solving accuracy and the number of models. ShiAlg needs 9600 rules because these rules are semantics based.

After we have compared PROPOSED with the baseline algorithms, we conduct an ablation experiment to show the contribution of the relaxed S\(^{2}\) method and QRAN to the accuracy of PROPOSED solving AWPs. Concretely, we investigate how much the relaxed S\(^{2}\) method and QRAN contribute to increase the accuracy of the whole PROPOSED. Table 6 presents the results of this ablation experiment. In Table 6, “Not-Relaxed” means the PROPOSED uses the original S\(^{2}\) method but not the relaxed S\(^{2}\) method; “No-QRAN” means that we run PROPOSED without the function of adding implicit relations; “No-Both” means the PROPOSED does not use either the relaxed S\(^{2}\) method or the function of adding implicit relations.

Table 6 tells three conclusions. The first conclusion is that the relaxed S\(^{2}\) method increases the accuracy of PROPOSED solving AWPs by at least 6.3% at any dataset. The second one is that QRAN increases the accuracy of PROPOSED solving AWPs by from 1.9% to 45.6% on the different datasets. The third one is that the relaxed S\(^{2}\) method and QRAN together increase the accuracy of PROPOSED solving AWPs by from 8.8% to 48.6% on the different datasets.

Discussions on experimental results: For a given dataset, the implicit ratio is the ratio of implicit problems to total problems. The implicit ratio of EEP dataset is 39.7%. We use this ratio as the reference ratio because the problems in EEP dataset are from entrance exam papers. The implicit ratios of M23K, Dol2K, and Arith are 20.8%, 3.7%, and 31.7%, respectively. Implicit ratios of M23K and Dol2K can thus be deemed low, compared with the reference ratio. This discloses the fact that most of the existing algorithms focus on solving explicit problems because they are tested only on the datasets with low implicit ratio. Arith is the only dataset that is used to test the algorithm that can extract some implicit relations. Hence, its implicit ratio is higher than the other datasets, though it is still lower than the reference ratio by 8%. Interestingly, RoyAlg achieved high accuracy, being 73.8% and 85.5% on USC and Arith in English, respectively. However, the accuracies that RoyAlg works on other datasets are lower than 62%. It seems that RoyAlg is sensitive to the problem type.

For the evaluation in the baseline algorithms, an algorithm is said that it can correctly solve an AWP if its output can correctly match to the ground-truth, but they do not check whether all the transforms of producing the correct answers are correct. Thus, we discover the phenomenon that some seq2seq algorithms may give correct answers using wrong answer expressions. Table 7 shows two examples of this phenomenon. In the first example, the algorithm does not figure out the concept of “average speed of round trip”, and mistakenly takes \(n_{3}\) as a multiple of total distance. In the second example, the model does not understand the concept of “half of the book”, and coincidentally takes \(n_{3}\) as a multiple of the number of pages read. Such confusion of mathematical concepts would lead to wrong answers while problem statements might have some changes.

For the task of acquiring implicit relation by neural network miner, this paper has tried other models, such as Word2Vec, GLOVE, and FastText, but we find that the BERT model suits the task. The BERT model can capture the overall semantic differences of the problem text and the semantic differences of entities in different scenarios, thus it achieves better experimental results. For example, when the feature word “rectangle” appears in the problem text, it needs to figure out that the arithmetic scene is about the area or the perimeter. There are some other improved models after the BERT model, such as RoBERTa, GPT3, XLNET, and T5. These models maybe improve the accuracy of our algorithm in acquiring implicit relations. However, the main objective of this paper is to verify the effectiveness of the idea of transforming the complex task of solving AWPs into the smaller task of relation acquisition and transformation. The experimental results demonstrate that the relation-centric solving algorithm has achieved better results using the BERT model. Thus, we have not explored the models proposed after BERT. On the other hand, these models are similar in principle to the BERT model, although they may use some techniques for specific tasks and enhance the training data.

Table 7 Two examples that the seq2seq algorithms have the correct answer through evaluating wrong answer expressions
Full size table

Among the five baseline algorithms, the seq2seq algorithms have claimed the highest performances in terms of answer accuracy. However, this accuracy is not a reliable accuracy because these algorithms have some false positive instances. This paper has given two examples of false positive instances in Table 7. Compared with the five baseline algorithms, the proposed algorithm has three common main advantages. The first one is that it has no false positive instances. The second one is that it broadens the range of solving arithmetic word problems, especially in solving implicit problems, outperforming state-of-the-art algorithms on all nine datasets. The third is that it is explainable because its actions of acquiring and transforming relations are understandable. More importantly, this series of actions can instruct students on how to solve the problem.

Conclusions and future work

This paper has taken the decomposition strategy to tackle the research problem of designing algorithms for solving AWPs. Following this notion, it has innovated a three-phase scheme of designing a high performance algorithm for solving AWPs. This three-phase scheme can break the heavy task of developing algorithms for solving AWPs into three smaller tasks. The first phase is to build a solving algorithm paradigm that summarizes and explains all algorithms for solving AWPs. The second phase is to form relation-centric approach by instantiating the solving algorithm paradigm. The third phase is to instantiate the relation-centric approach by proposing the methods to acquire the relations and to transform relations.

Fig. 5
figure 5

The loss and accuracy graph of the training and validation of QRAN. Variation of accuracy with epochs is in (a); variation of loss with epochs is in (b)

Full size image

The proposed algorithm designed using three-phasescheme has three desired characteristics. The first one is that it is explainable, thanks to the fact that it solves AWPs with explicitly stated rules, models and algorithm actions. It is a very important characteristics that the algorithms output the explainable solution because it is an indispensable characteristics for building the tutoring function. In contrast, ZhaoAlg in [9] and LinAlg in [12] are not explainable because they solve the problems within a pure seq2seq approach. The second one is that the proposed algorithm has a neural network miner dedicated to acquiring implicit relations. Thus, it formed a procedure that synergizing the S\(^{2}\) extractor for extracting explicit relations and the neural network miner for acquiring implicit relations. The last one is that it is a high performance algorithm. It outperforms all the baseline algorithms in terms of the number of used models and accuracy of solving AWPs. In addition to, it outputs an algorithmic solution to show a correct transforming process when it can solve the given AWP.

This paper has four technical contributions. First, it designed and implemented a three-phase scheme of designing solving algorithms. Second, it proposed a state-action algorithm paradigm. Third, it formed the relation-centric approach of solving AWPs. Fourth, it built a procedure of synergizing a relaxed S\(^{2}\) method for extracting explicit relations and a neural network miner for acquiring implicit relations.

Three research areas among many potential ones could be further investigated in the near future. First, it is expected to adopt the three-phase scheme to design more solving algorithms. Second, it is feasible to develop the vector computing procedure to replace the text processing part of S\(^{2}\) method. Third, it is anticipated to develop novel intelligent tutoring systems based on the new solving algorithms, which has been the ultimate motivation of our research.