Convergence and gradient algorithm of a class of neural networks based on the polygonal fuzzy numbers representation

Abstract

As a special case of general fuzzy numbers, the polygonal fuzzy number can describe a fuzzy object by means of an ordered representation of finite real numbers. Different from general fuzzy numbers, the polygonal fuzzy numbers overcome the shortcoming of complex operations based on Zadeh’s traditional expansion principle, and can maintain the closeness of arithmetic operation. Hence, it is feasible to use a polygonal fuzzy number to approximate a general fuzzy number. First, an extension theorem of continuous functions on a real compact set is given according to open set construction theorem. Then using Weierstrass approximation theorem and ordered representation of the polygonal fuzzy numbers, the convergence of a single hidden layer feedforward polygonal fuzzy neural network is proved. Secondly, the gradient vector of the approximation error function and the optimization parameter vector of the network are given by using the ordered representation of polygonal fuzzy numbers, and then the gradient descent algorithm is used to train the optimal parameters of the polygonal fuzzy neural network iteratively. Finally, two simulation examples are given to verify the approximation ability of the network. Simulation result shows that the proposed network and the gradient descent algorithm are effective, and the single hidden layer feedforward network have good abilities in learning and generalization.

Introduction

Artificial neural network has the ability of processing nonlinear information adaptively, and it also can overcome the shortcomings of traditional artificial intelligence methods in intuitive pattern, speech recognition, and unstructured information processing. Therefore, neural networks have been successfully applied in fields of expert system, pattern recognition and intelligent control. In fact, most of the previous study on approximation problems of neural networks stays on the existence of networks, and to realize the construction of network, complex algorithm design and program operation are needed. In 1994, Chen [1] first proposed the approximation problem of system identification using neural network. It was proved that integrable functions on compact set can be approximated by the linear composition of continuous functions of one variable, and a method of identifying dynamic system with the neural network was presented. In 2003, Cao and Xu [2] studied the problem of using a single hidden layer neural network to approximate a continuous function by taking the best polynomial approximation as a measure, and methods of the network construction and approximation speed estimation are proposed. Later, Cao and Zhang et al. [3] gave an algorithm of using neural network to approximate a continuous function in a special distance space. In 2008, Xie et al. [4] proved the existence of single hidden layer neural network interpolation under some certain conditions satisfied for activation function, and a calculation method of connection weights and threshold was given simultaneously. In 2009, Xu and Cao et al. [5] studied the approximation error of using this kind of network interpolation to approximate an objective function. These results greatly expand the further research on the construction method and approximation performance of the single hidden layer neural networks.

As early as 1987, Prof. Kosko first proposed the concept of fuzzy neural network by combining fuzzy set with artificial neural network. And then in 1992, Kosko proved that fuzzy systems can approximate real continuous functions on compact sets with arbitrary precision [6, 7]. In 1992, Wang and Mendel [8] proved that the Gaussian fuzzy logic system is a uniform approximator. Meanwhile, a meaningful issue of “Can fuzzy neural network be used as a tool to approximate fuzzy function?” was presented in [8]. In 1994, Buckley et al. first studied the problem of using fuzzy neural networks to approximate continuous fuzzy functions [9, 10], and then in 1999, aimed at the issue presented in [8], he pointed out that hybrid fuzzy neural networks can constitute universal approximators for fuzzy functions in [11], yet regular fuzzy neural networks do not. In addition, Buckley conjectured that regular fuzzy neural networks have a universal approximation for continuously increasing fuzzy functions. Thereafter, through the systematic research on regular networks, scholars made some important breakthroughs [12,13,14]. These results have important theoretical value for further research on fuzzy reasoning, fuzzy control and image restoration technology. Unfortunately, arithmetic operations involved in the above results are all based on traditional Zadeh’s extension principle, thus these operations are not closed in fuzzy number space. For example, arithmetic operations are not closed even for simple triangular fuzzy numbers and trapezoidal fuzzy numbers. This disadvantage hinders the wide application of fuzzy number theory. Therefore, how to approximately implement the linear arithmetic operation for general fuzzy numbers is a key problem worthy of attention.

In 2002, Liu [15] first proposed the concept of n-symmetric polygonal fuzzy number based on the idea of segmentation, which overcome the difficulty of Zadeh’s extension principle-based arithmetic operation. A polygonal fuzzy neural network (PFNN) model was established initially, and arithmetic operation and fuzzy information processing of n-PFNs were given through the representation of finite ordered real numbers. In 2011, Wang and Li [16] gave an improved concept of n-PFN in the case of equidistant segmentation, and the ordered representation of n-PFN was also proposed. And then the linearization operations of some general fuzzy numbers were realized by transforming general fuzzy numbers into the ordered representation of n-PFNs. In 2012, Baez and Moretti et al. proposed another representation for the polygonal fuzzy numbers and extended it to fuzzy sets on ${{{\mathbb {R}}}^{n}}$. It was proved that fuzzy set family can constitute a complete separable space when given a generalized Hausdorff metric in [17]. In 2014, Wang and Li [18] discussed the universal approximation of a class of PFNN by introducing the concepts of induction operator and K-integral norm. See [19]. In fact, PFNN is a new network system which is based on an artificial neural network and ordered representation of n-PFN. Its main feature is that connection weights and threshold of the network are both n-PFNs. PFNN mainly uses linear operations of n-PFNs to adjust the parameters directly, PFNN has the characteristics of easy implementation and strong approximation ability.

In 2012, He and Wang [20] designed a conjugate gradient algorithm for the PFNN based on the extended the arithmetic operations of PFNs. See [21]. In 2014, Yang and Wang et al. [22] designed a GA-BP hybrid algorithm to optimize parameters of PFNN by combining the genetic algorithm and BP algorithm. In 2016, Li and Li [23] constructed a single input single output PFNN by means of equidistant partition of domain and interpolation function. In 2018, Wang and Suo [24] designed the connection weights and threshold parameters, and proposed the isolation layered algorithm of the multiple input multiple output PFNN. See [25]. In 2021, Wang and Chen [26] further established the neural network model of the T-S fuzzy system by using the ordered representation of n-PFNs, and proposed the TS firefly algorithm of non-homogeneous linear polygonal T-S fuzzy system based on the flight characteristics of fireflies. See [27,28,29,30]. These neural networks constructed by the ordered representation of n-PFNs show the superior performance of PFNN from different aspects.

In 2013, Garg and Sharma [31] first proposed a redundancy allocation problem for multi-objective reliability based on particle swarm optimization (PSO), analyzed the performance of the complex repairable industrial system by using the lambda-tau method of the fuzzy confidence interval, and a hybrid PSO-GA for solving constrained optimization problem was put forward. See [32, 33]. In 2016, Gaxiola and Melin et al. [34] used genetic algorithm and PSO to optimize the type-2 fuzzy inference system, and applied the optimized type-2 fuzzy inference system to estimate the type -2 fuzzy weight of bacpropagation neural network. See Refs. [35,36,37]. Later, Agrawal and Pal et al. did a lot of excellent work by using PSO algorithm and generalized type-2 fuzzy set in [38, 39]. Especially, Khater and Ding et al. studied the adaptive online learning and multivariable time series analysis for a class of recurrent fuzzy neural networks in [40, 41], respectively. In 2019, Hsieh and Jeng [42] utilized locally weighted polynomial regression to propose a single index fuzzy neural network, and used output an activation function and polynomial function to approximate the constructed network. In 2021, Wang and Xiao [43] constructed an interpolation neural network using the step path method and proved that the network has approximation performance. These fuzzy neural networks and their algorithms not only show their advantages in different aspects, but also lay a theoretical foundation for their further wide application.

The main contributions of this paper include two aspects: one is to prove the convergence of single hidden layer feedforward PFNN based on the extension theorem on a compact set, Weierstrass approximation theorem and the ordered representation of n-PFNs; the other is to propose the gradient vector of the approximation error function and the optimization parameter vector of the constructed network through the operation rules of n-PFNs, and utilize the gradient descent algorithm to iteratively train some optimization parameters of PFNN, so as to design an optimization algorithm. These results lay a foundation for the next step to combine with ordinary neural network to show its unique advantage in pattern recognition and information processing. The main innovation is that n-PFNs and its ordered representations are introduced to describe the input and output expressions of a class of fuzzy neural networks, and an optimization algorithm is designed to realize the linearization of this kind of neural networks. This is mainly because the proposed n-PFNs and their operations do not depend on the traditional Zadeh’s extension principle. They not only overcome the complexity of traditional fuzzy number operations, but also realize linearization operations. This is undoubtedly the key to the introduction of n-polygonal fuzzy number. Besides, the backpropagation (BP) algorithm can be designed based on the gradient descent method. It is more suitable for the learning algorithm of a multilayer neural network. Generally, its input and output is a nonlinear mapping relationship, and its information processing ability mainly comes from the multiple combinations of simple nonlinear functions. However, the proposed n-PFNs can not only approximate the general fuzzy number with arbitrary accuracy, but also satisfy the linear operation. Therefore, using the ordered representations of n-PFNs as the input and output of a single hidden layer fuzzy neural network is a linear mapping, which makes the designed algorithm easier to realize the multiple replication ability and information processing ability of nonlinear function than the backpropagation algorithm.

Because the general fuzzy number can not simply achieve the linear operations, it can only rely on Zadeh’s extension principle to carry out quite complex arithmetic operations, which has always been a key problem obstructing the development and application of fuzzy number theory. However, the proposed n-PFNs is not only the generalization of triangular or trapezoidal fuzzy numbers, but also any fuzzy number can be transformed into an n-PFNs by the number of subdivision n, so as to avoid Zadeh’s expansion principle, realize linear operations and maintain the closeness of arithmetic operations. In addition, polygonal fuzzy numbers can be described by finite ordered real numbers (ordered representation), it not only overcomes the complexity of the operation of general fuzzy numbers, but also maintains some excellent properties of the trapezoidal fuzzy numbers, and can approach general fuzzy numbers with arbitrary accuracy. Therefore, they have obvious advantages in fuzzy information processing. This is our main motivation to introduce n-PFNs as a basic tool to adjust parameters of the proposed feedforward PFNN.

The main contents of each section are as follows. In “n-polygonal fuzzy numbers (n-PFNs)”, we review some basic concepts of n-PFNs, polygonal fuzzy value function, single layer feedforward neural network, and so on. Some important lemmas and related arithmetic operations are also given in this section. In “Convergence of the neural network”, based on the continuation theorem of continuous function and Weierstrass approximation theorem, a single hidden layer feedforward polygonal fuzzy neural network model is established, and the convergence of the network is proved. In “Gradient descent algorithm”, a gradient descent algorithm-based parameter vector iteration optimization method is designed to implement the network training. In “Simulation examples”, two simulation examples are given to verify the effectiveness and advantages of the proposed approach. In “Conclusion”, the main works of this paper are summarized.

n-polygonal fuzzy numbers (n-PFNs)

General fuzzy numbers can’t simply carry out linear operations, but can only carry out more complex arithmetic operations by Zadeh’s extension principle, which hinders the development and application of fuzzy number theory. Hence, it is of positive significance to introduce the concept of polygonal fuzzy number and discuss its extended operations. For the sake of consistency in the expression of the whole paper, ${\mathbb {N}}$ indicates natural number set, ${\mathbb {R}}$ is a real number set, ${{F}_{0}}({\mathbb {R}})$ indicates the set of all fuzzy numbers on ${\mathbb {R}}$, where each fuzzy number $A\in {{F}_{0}}({\mathbb {R}})$ satisfies (1)–(2): (1) there is ${{x}_{0}}\in {\mathbb {R}}$ so that $A({{x}_{0}})=1$; (2) for any $\alpha \in (0,1]$, the cut set ${{A}_{\alpha }}$ is a bounded closed interval on ${\mathbb {R}}$.

Basic definition and ordered representation

Definition 1

For a given fuzzy number $A\in {{F}_{0}}({\mathbb {R}})$ and $n\in {\mathbb {N}}$, if the membership function of A has the following form:

$$\begin{aligned} A(x)\!=\!\left\{ \begin{array}{ll} \frac{{1}/{n}}{a_{i}^{1}-a_{i-1}^{1}}\left( x-a_{i-1}^{1}\right) +\frac{i-1}{n}, &{} x\in \left[ a_{i-1}^{1},a_{i}^{1}\right) , \\ &{} i =1,2,\ldots ,n, \\ 1, &{} x\in \left[ a_{n}^{1},a_{n}^{2}\right] , \\ -\frac{{1}/{n}}{a_{i-1}^{2}-a_{i}^{2}}\left( x-a_{i-1}^{2}\right) +\frac{i-1}{n}, &{} x\in \left( a_{i}^{2},a_{i-1}^{2}\right] , \\ &{} i =n,n-1,\ldots ,1, \\ 0, &{} x\in \left( -\infty ,a_{0}^{1}\right) \text {or } \\ &{} x\in \left( a_{0}^{2},+\infty \right) , \end{array}\right. \end{aligned}$$

(1)

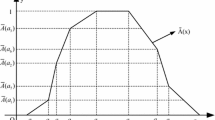
where $a_{0}^{1}\le a_{1}^{1}\le \cdots \le a_{n}^{1}\le a_{n}^{2}\le \cdots \le a_{1}^{2}\le a_{0}^{2}$, then A is called an n-polygonal fuzzy number on ${\mathbb {R}}$, and A is also abbreviated as n-PFN, the $2n+2$ ordered real numbers $\left\{ a_{0}^{1},a_{1}^{1},\ldots ,a_{n}^{1},a_{n}^{2},\ldots ,a_{1}^{2},a_{0}^{2}\right\}$ is called an ordered representation of A, it is expressed as $A\!=\!\left( a_{0}^{1},a_{1}^{1},\ldots ,a_{n}^{1},a_{n}^{2},\ldots ,a_{1}^{2},a_{0}^{2} \right)$. For a geometric explanation of the membership function A(x), see the following Fig. 1.

Fig. 1

The membership function image of an n-PFN A

According to Eq. (1), it can be known that the membership function of A is continuous, and its image consists of straight line segments. As shown in Fig. 1. It is obvious that the support set and the kernel of A are $\text {Supp}A=(a_{0}^{1},a_{0}^{2})$ and $\text {Ker}A=[a_{n}^{1},a_{n}^{2}]$, respectively.

Since the membership function A(x) can be described by $2n+2$ intersections completely, the n-PFN A can be simply represented by the group of intersections. That is $\left( a_{0}^{1},0\right) , \left( a_{1}^{1},\frac{1}{n}\right) , \ldots , \left( a_{n}^{1},\frac{n}{n}\right) , \left( a_{n}^{2},\frac{n}{n}\right) , \ldots ,\left( a_{1}^{2},\frac{1}{n}\right) , \left( a_{0}^{2},0\right) .$

Furthermore, since ordinates of these intersections are determined, the n-PFN can be simply represented by the ordered array of abscissas. Thereby, each n-PFN can be uniquely expressed as an ordered representation of $2n+2$ real numbers. On the contrary, the membership function of an n-PFN can also be obtained directly from the ordered representation of the n-PFN in accordance with (1). See the example below.

Example 1

Let an ordered representation $A= \Big (-3,-2,0, \frac{3}{2},\frac{5}{2},\frac{10}{3},6,7\Big )$, please calculate its corresponding membership function of n-polygonal fuzzy number A (Fig. 2).

In fact, since there are eight real numbers in A, let $2n+2=8$ implies $n=3$, their divided points ${{\lambda }_{1}}=\frac{1}{3}$, ${{\lambda }_{2}}=\frac{2}{3}$. It is not difficult to obtain the inflection point coordinates of 3-polygonal fuzzy number A as

$$\begin{aligned}&\left( -3,0\right) , \left( -2,\frac{1}{3}\right) , \left( 0,\frac{2}{3}\right) , \left( \frac{3}{2},1\right) , \left( \frac{5}{2},1\right) , \left( \frac{10}{3},\frac{2}{3}\right) , \\&\left( 6,\frac{1}{3}\right) , \left( 7,0\right) .\end{aligned}$$

Connecting the adjacent inflection points in order with straight line segments, we can get that the membership function and image of A be expressed as

$$\begin{aligned}A(x)=\left\{ \begin{array}{ll} \frac{x}{3}+1, &{} -3\le x<-2, \\ \frac{x}{6}+\frac{2}{3}, &{} -2\le x<0, \\ \frac{2x}{9}+\frac{2}{3}, &{} 0\le x<\frac{3}{2}, \\ 1, &{} \frac{3}{2}\le x\le \frac{5}{2}, \\ -\frac{2x}{5}+2, &{} \frac{5}{2}<x\le \frac{10}{3}, \\ -\frac{x}{8}+\frac{13}{12}, &{} \frac{10}{3}<x\le 6, \\ -\frac{x}{3}+\frac{7}{3}, &{} 6<x\le 7, \\ 0, &{} \text {Otherwise}. \end{array}\right. \end{aligned}$$

Fig. 2

The membership function image of 3-PFN $Z_{3}(A)$

For ordered representations of n-PFNs, there may be some special cases. For example, if there are $i\in \left\{ 1,2,\ldots ,n \right\}$ and $q\in \left\{ 1,2 \right\}$, and hold $a_{i-1}^{q}=a_{i}^{q}$ for two adjacent intersections, then the corresponding straight line segment of membership function image is vertical. For a more special case of $a_{0}^{1}=a_{1}^{1}=\cdots =a_{n}^{1}=a_{n}^{2}=\cdots =a_{1}^{2}=a_{0}^{2}$, A degenerates to a single point fuzzy number, and its membership function image is a vertical line segment. In general, we assume that the inequality $a_{0}^{1}\le a_{1}^{1}\le \cdots \le a_{n}^{1}\le a_{n}^{2}\le \cdots \le a_{1}^{2}\le a_{0}^{2}$ holds strictly, that is $a_{0}^{1}<a_{1}^{1}<\cdots<a_{n}^{1}<a_{n}^{2}<\cdots<a_{1}^{2}<a_{0}^{2}$. It should be pointed out that this assumption will not affect the subsequent discussion and conclusion.

Let $F_{0}^{tn}({\mathbb {R}})$ be the set of n-PFNs on ${\mathbb {R}}$. Then it is obvious that $F_{0}^{tn}({\mathbb {R}})\subset {{F}_{0}}({\mathbb {R}})$. In particular, when $n=1$, the 1-PFN degenerates into a trapezoid fuzzy number or triangle fuzzy number. For an n-PFN ($n\ge 2$), if its membership function image is regarded as the superposition of n small trapezoids or triangle, then the n-PFN can be seen as a generalization of trapezoid fuzzy numbers or triangle fuzzy number.

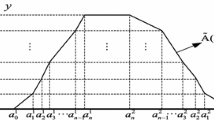
An important significance of introducing the concept of n-PFNs is that a general fuzzy number can be approximately represented by an n-PFN. In fact, for a general fuzzy number, an n-PFN can be determined according to the value of n. The operation can be described by the following Fig. 3, where ${{Z}_{n}}(\cdot )$ denotes the membership function of the determined n-PFN. It is not difficult to see from Fig. 3 that the determined n-PFN mainly depends on abscissas of $2n+2$ points on A(x).

Fig. 3

A general fuzzy number and its approximation of n-PFN

It is obvious that the larger the number n is, the more trapezoids or triangle will be obtained, and then the stronger its ability to approximate the general fuzzy number will be. It is of course, with the increase of n, the complexity of the n-PFN increases.

Arithmetic operations and metric

Definition 2

[15, 16] For a given $n\in {\mathbb {N}}$, if $A,B\in$ $F_{0}^{tn}({\mathbb {R}})$, where $A=\left( a_{0}^{1},a_{1}^{1},\ldots ,a_{n}^{1},a_{n}^{2},\ldots ,a_{1}^{2},a_{0}^{2}\right)$, $B=$ $\left( b_{0}^{1},b_{1}^{1},\ldots ,b_{n}^{1},b_{n}^{2},\ldots ,b_{1}^{2},b_{0}^{2} \right)$, then the corresponding arithmetic operations in $F_{0}^{tn}({\mathbb {R}})$ are defined as follows:

• 1) $A+B=\big (a_{0}^{1}+b_{0}^{1},a_{1}^{1}+b_{1}^{1},\ldots ,a_{n}^{1}+b_{n}^{1},a_{n}^{2}+ b_{n}^{2}, \ldots , a_{1}^{2}+b_{1}^{2},a_{0}^{2}+b_{0}^{2}\big );$

• 2) $A-B=\big (a_{0}^{1}-b_{0}^{2},a_{1}^{1}-b_{1}^{2},\ldots ,a_{n}^{1}-b_{n}^{2},a_{n}^{2}-b_{n}^{1},\ldots ,a_{1}^{2}-b_{1}^{1},a_{0}^{2}-b_{0}^{1}\big );$

• 3) $A\cdot B=\left( c_{0}^{1},c_{1}^{1},\ldots ,c_{n}^{1},c_{n}^{2},\ldots ,c_{1}^{2},c_{0}^{2}\right) ,$ where $c_{i}^{1}=a_{i}^{1}b_{i}^{1}\wedge a_{i}^{1}b_{i}^{2}\wedge a_{i}^{2}b_{i}^{1}\wedge a_{i}^{2}b_{i}^{2}$, $c_{i}^{2}=a_{i}^{1}b_{i}^{1}\vee a_{i}^{1}b_{i}^{2}\vee a_{i}^{2}b_{i}^{1}\vee a_{i}^{2}b_{i}^{2}$, $i=0,1,\ldots ,n$;

• 4) $k\cdot A=\left\{ \begin{array}{llll} \left( ka_{0}^{1},ka_{1}^{1},\ldots ,ka_{n}^{1},ka_{n}^{2},\ldots ,ka_{1}^{2},ka_{0}^{2}\right) , &{} k{>}0, \\ \left( ka_{0}^{2},ka_{1}^{2},\ldots ,ka_{n}^{2},ka_{n}^{1},\ldots ,ka_{1}^{1},ka_{0}^{1}\right) , &{} k{<}0. \end{array}\right.$

From Definition 2, it can be obtained that compared with general fuzzy number space ${{F}_{0}}({\mathbb {R}})$, the arithmetic operations in n-PFN space $F_{0}^{tn}({\mathbb {R}})$ are simple.

Let $\sigma :{\mathbb {R}}\rightarrow {\mathbb {R}}$ be a continuously increasing activation function, $n\in {\mathbb {N}}$, we extend the $\sigma$ as $\sigma : F_{0}^{tn}({\mathbb {R}})\rightarrow F_{0}^{tn}({\mathbb {R}})$. That is to say, if $A=\left( a_{0}^{1},a_{1}^{1},\ldots ,a_{n}^{1},a_{n}^{2},\ldots ,a_{1}^{2},a_{0}^{2}\right) \in F_{0}^{tn}({\mathbb {R}})$, we can define $\sigma (A)=\big (\sigma (a_{0}^{1}),\sigma (a_{1}^{1}),\ldots ,\sigma (a_{n}^{1}),\sigma (a_{n}^{2}),\ldots ,\sigma (a_{1}^{2}),\sigma (a_{0}^{2})\big )\in F_{0}^{tn}({\mathbb {R}})$.

If $n\in {\mathbb {N}}$, the mapping ${{Z}_{n}}:{{F}_{0}}({\mathbb {R}})\rightarrow F_{0}^{tn}({\mathbb {R}})$, then ${{Z}_{n}}$ is called an $n-$polygonal operator. In other words, for any $A\in {{F}_{0}}({\mathbb {R}})$, there is an n-PFN $B\in F_{0}^{tn}({\mathbb {R}})$ such that ${{Z}_{n}}(A)=B$. In general, it is easy to obtain the n-PFN ${{Z}_{n}}(A)$ corresponding to $A\in {{F}_{0}}({\mathbb {R}})$. See Example 2 below.

Definition 3

[45] Let two given fuzzy numbers $A,~B\in {{F}_{0}}({\mathbb {R}})$ and $n\in {\mathbb {N}}$, and their ordered representations are ${{Z}_{n}}(A)=\left( a_{0}^{1},a_{1}^{1},\ldots ,a_{n}^{1}, a_{n}^{2},\ldots ,a_{1}^{2},a_{0}^{2}\right)$, ${{Z}_{n}}(B)=\left( b_{0}^{1},b_{1}^{1},\ldots ,b_{n}^{1},b_{n}^{2},\ldots ,b_{1}^{2},b_{0}^{2}\right)$, define the addition, subtraction and multiplication as follows:

• 1) ${{Z}_{n}}(A)+{{Z}_{n}}(B)=\big (a_{0}^{1}+b_{0}^{1},a_{1}^{1}+b_{1}^{1},\ldots ,a_{n}^{1}+b_{n}^{1},a_{n}^{2}+b_{n}^{2},\ldots ,a_{1}^{2}+b_{1}^{2},a_{0}^{2}+b_{0}^{2}\big );$

• 2) ${{Z}_{n}}(A)-{{Z}_{n}}(B)=\big (a_{0}^{1}-b_{0}^{2},a_{1}^{1}-b_{1}^{2},\ldots ,a_{n}^{1}-b_{n}^{2},a_{n}^{2}-b_{n}^{1},\ldots ,a_{1}^{2}-b_{1}^{1},a_{0}^{2}-b_{0}^{1}\big );$

• 3) ${{Z}_{n}}(A)\cdot {{Z}_{n}}(B)=\left( c_{0}^{1},c_{1}^{1},\ldots ,c_{n}^{1},c_{n}^{2},\ldots ,c_{1}^{2},c_{0}^{2}\right) ,$ where $c_{i}^{1}=a_{i}^{1}b_{i}^{1}\wedge a_{i}^{1}b_{i}^{2}\wedge a_{i}^{2}b_{i}^{1}\wedge a_{i}^{2}b_{i}^{2}$ and $c_{i}^{2}=a_{i}^{1}b_{i}^{1}\vee a_{i}^{1}b_{i}^{2}\vee a_{i}^{2}b_{i}^{1}\vee a_{i}^{2}b_{i}^{2}$, $i=0,1,2,\ldots ,n$;

• 4) $k\cdot {{Z}_{n}}(A)=\left( ka_{0}^{1},ka_{1}^{1},\ldots ,ka_{n}^{1},ka_{n}^{2},\ldots ,ka_{1}^{2},ka_{0}^{2} \right) ,$ where $k>0$.

Proposition 1

[16] Let $A,B\in {{F}_{0}}({\mathbb {R}})$, for a given $n\in {\mathbb {N}}$, then the following properties hold:

• 1) ${{Z}_{n}}(A\pm B)={{Z}_{n}}(A)\pm {{Z}_{n}}(B)$,  ${{Z}_{n}}(A\cdot B)={{Z}_{n}}(A)\cdot {{Z}_{n}}(B);$

• 2) ${{Z}_{n}}\left( {{Z}_{n}}(A)\right) ={{Z}_{n}}(A)$,  ${{Z}_{n}}(k\cdot A)=k\cdot {{Z}_{n}}(A)$, where k can also be regarded as a set $\{k\}$.

Example 2

Let the membership functions of the fuzzy numbers A and B be expressed as

$$\begin{aligned} A(x)= & {} \left\{ \begin{array}{ll} \sqrt{2x+2}-1, &{} -\frac{1}{2} \le x< 1, \\ 1, &{} 1 \le x \le 2, \\ \sqrt{2-\frac{x}{2}}, &{} 2< x \le 4, \\ 0, &{} \text {Otherwise}; \end{array}\right. \\ B(x)= & {} \left\{ \begin{array}{ll} \frac{3x}{x+1}, &{} 0 \le x< \frac{1}{2}, \\ 1, &{} \frac{1}{2} \le x \le 1, \\ \frac{2}{x}-1, &{} 1 < x \le 2, \\ 0, &{} \text {Otherwise}. \end{array}\right. \end{aligned}$$

Obviously, $\text {Supp}A=\left[ -\frac{1}{2},4\right]$, $\text {Ker}A=[1,2]$; $\text {Supp}B=[0,2]$, $\text {Ker}A=\left[ \frac{1}{2},1\right]$.

For example, for the fuzzy number A, if $n=3$, we choose the divided points ${{\lambda }_{1}}={1}/{3}$ and ${{\lambda }_{2}}={2}/{3}$. When $x\in [-{1}/{2},1)$, let $A(x)=\sqrt{2x+2}-1=\frac{1}{3},\frac{2}{3}$, then ${{x}_{1}}=-\frac{1}{9}$ and ${{x}_{2}}=\frac{7}{18}$ can be solved, respectively; when $x\in (2,4]$, let $A(x)=\sqrt{2-\frac{x}{2}}=\frac{1}{3},\frac{2}{3}$, then ${{x}_{3}}=\frac{34}{9}$ and ${{x}_{4}}=\frac{28}{9}$ can be solved, respectively.

Hence, the ordered representation of 3-polygonal fuzzy number ${{Z}_{3}}(A)$ can be obtained as

$$\begin{aligned}{{Z}_{3}}(A)= \left( -\frac{1}{2}, -\frac{1}{9},\frac{7}{18},1,2,\frac{28}{9},\frac{34}{9},4\right) .\end{aligned}$$

Similarly, if $n=4$, we choose the divided points ${{\lambda }_{1}}=\frac{1}{4}$, ${{\lambda }_{2}}=\frac{2}{4}$ and ${{\lambda }_{3}}=\frac{3}{4}$, and let $A(x)=\sqrt{2x+2}-1=\frac{1}{4},\frac{2}{4},\frac{3}{4}$ and $A(x)=\sqrt{2-\frac{x}{2}}=\frac{1}{4},\frac{2}{4},\frac{3}{4}$. It is not difficult to obtain the ordered representation of 4-polygonal fuzzy number ${{Z}_{4}}(A)$ as

$$\begin{aligned}{{Z}_{4}}(A)=\left( -\frac{1}{2},-\frac{7}{32},\frac{1}{8},\frac{17}{32},1,2,\frac{23}{8},\frac{7}{2},\frac{31}{8},4\right) .\end{aligned}$$

Using the same method, we can also easily solve other ordered representations, such as

$$\begin{aligned}{{Z}_{2}}(A)= & {} \left( -\frac{1}{2},\frac{1}{8},1,2,\frac{7}{2},5\right) ,\\ {{Z}_{2}}(B)= & {} \left( 0,\frac{1}{5},\frac{1}{2},1,\frac{4}{3},2\right) ;\\ {{Z}_{3}}(B)= & {} \left( 0,\frac{1}{8},\frac{2}{7},\frac{1}{2},1,\frac{6}{5},\frac{3}{2},2\right) , ~~ \\ {{Z}_{4}}(B)= & {} \left( 0,\frac{1}{11},\frac{1}{5},\frac{1}{3},\frac{1}{2},1,\frac{8}{7},\frac{4}{3},\frac{8}{5},2\right) .\end{aligned}$$

According to the membership functions A(x) or B(x) and their ordered representations, we can easily draw their images as follows (Figs. 4, 5, 6, 7):

Fig. 4

Images of A(x) and ${{Z}_{3}}(A)(x)$ when $n=3$

Fig. 5

Images of B(x) and ${{Z}_{3}}(B)(x)$ when $n=3$

Fig. 6

Images of A(x) and ${{Z}_{4}}(A)(x)$ when $n=4$

Fig. 7

Images of B(x) and ${{Z}_{4}}(B)(x)$ when $n=4$

Clearly, it is not difficult to calculate the analytic expressions of membership function ${{Z}_{n}}(A)(x)$ and ${{Z}_{n}}(B)(x)$. For example, when $n=3$, we have

$$\begin{aligned} {{Z}_{3}}(A)(x)= & {} \left\{ \begin{array}{llll} \frac{6x}{7}+\frac{3}{7}, &{} -\frac{1}{2} \le x< -\frac{1}{9}, \\ \frac{2x}{3}+\frac{11}{27}, &{} -\frac{1}{9} \le x< \frac{7}{18}, \\ \frac{6x}{11}+\frac{5}{11}, &{} \frac{7}{18} \le x< 1, \\ 1, &{} 1 \le x \le 2, \\ -\frac{3x}{10}+\frac{8}{5}, &{} 2< x \le \frac{28}{9}, \\ -\frac{x}{2}+\frac{17}{9}, &{} \frac{28}{9}< x \le \frac{34}{9}, \\ -\frac{3x}{2}+6, &{} \frac{34}{9}< x \le 4, \\ 0, &{} \text {Otherwise}; \end{array} \right. \\ {{Z}_{3}}(B)(x)= & {} \left\{ \begin{array}{llllll} \frac{8x}{3}, &{} 0 \le x< \frac{1}{8}, \\ \frac{56x}{27}+\frac{2}{27}, &{} \frac{1}{8} \le x< \frac{2}{7}, \\ \frac{14x}{9}+\frac{2}{9}, &{} \frac{2}{7} \le x< \frac{1}{2}, \\ 1, &{} \frac{1}{2} \le x \le 1, \\ -\frac{5x}{3}+\frac{8}{3}, &{} 1< x \le \frac{6}{5}, \\ -\frac{10x}{3}+2, &{} \frac{6}{5}< x \le \frac{3}{2}, \\ -\frac{2x}{3}+\frac{4}{3}, &{} \frac{3}{2} < x \le 2, \\ 0, &{} \text {Otherwise}. \end{array}\right. \end{aligned}$$

In addition, utilizing Definition 3 and Proposition 1 we can immediately obtain that

$$\begin{aligned} \left\{ \begin{aligned} {{Z}_{3}}(A+B)&={{Z}_{3}}(A)+{{Z}_{3}}(B)\\&=\left( -\frac{1}{2},\frac{1}{72},\frac{85}{126},\frac{3}{2},3,\frac{194}{45},\frac{95}{18},6 \right) , \\ {{Z}_{3}}(A-B)&={{Z}_{3}}(A)-{{Z}_{3}}(B)\\&=\left( -\frac{5}{2},-\frac{29}{18},-\frac{73}{90},0,\frac{3}{2},\frac{178}{63},\frac{263}{72},5 \right) , \\ {{Z}_{3}}(A\cdot B)&={{Z}_{3}}(A)\cdot {{Z}_{3}}(B)\\&=\left( -1,-\frac{1}{6},\frac{1}{9},\frac{1}{2},2,\frac{56}{15},\frac{17}{3},8 \right) . \end{aligned} \right. \end{aligned}$$

Similarly, when $n=4$ we have

$$\begin{aligned} \left\{ \begin{aligned} {{Z}_{4}}(A+B)&=\left( -\frac{1}{2},-\frac{45}{352},\frac{13}{40},\frac{83}{96},\frac{3}{2},3,\frac{225}{56},\frac{29}{6},\frac{219}{40},6 \right) , \\ {{Z}_{4}}(A-B)&=\left( -\frac{5}{2},-\frac{291}{160},-\frac{29}{24},-\frac{137}{224},0,\frac{3}{2},\frac{51}{24},\frac{33}{10},\frac{333}{88},4 \right) , \\ {{Z}_{4}}(A\cdot B)&=\left( -1,-\frac{7}{20},\frac{1}{40},\frac{17}{96},\frac{1}{2},2,\frac{23}{7},\frac{14}{3},\frac{31}{5},8 \right) . \end{aligned} \right. \end{aligned}$$

In other words, general fuzzy number operations $A\pm B$ and $A\cdot B$ can be approximately expressed as the ordered representations ${{Z}_{n}}(A\pm B)$ and ${{Z}_{n}}(A\cdot B)$, respectively. For example, when $n=3$, we have

$$\begin{aligned} \begin{aligned} A+B&\approx \left( -\frac{1}{2},\frac{1}{72},\frac{85}{126},\frac{3}{2},3,\frac{194}{45},\frac{95}{18},6 \right) , \\ A\cdot B&\approx \left( -1,-\frac{1}{6},\frac{1}{9},\frac{1}{2},2,\frac{56}{15},\frac{17}{3},8 \right) ; \end{aligned} \end{aligned}$$

when $n=4$,

$$\begin{aligned} A\cdot B\approx \left( -1,-\frac{7}{20},\frac{1}{40},\frac{17}{96},\frac{1}{2},2,\frac{23}{7},\frac{14}{3},\frac{31}{5},8 \right) . \end{aligned}$$

Remark 1

With the increase of n value, the approximation ability of ordered representation becomes stronger, but its complexity also increases. Therefore, it is very important to choose the appropriate n according to the actual needs. In addition, it is not difficult to see from the above operations that the proposed arithmetic operation does not rely on the traditional Zadeh’s extension principle, but only relies on the ordered representation given in Definition 3. In fact, these operations not only overcome the complexity of the traditional fuzzy number expansion operation, but also realize the linearization operation. This is undoubtedly the key to the introduction of n-polygonal fuzzy number. Especially, it has important applications in the approximation theory and optimization algorithm of fuzzy neural network.

In addition, $D(A,B)=\mathop {\sup }_{\alpha \in (0,1]}{{d}_{H}}({{A}_{\alpha }},{{B}_{\alpha }})$ is defined as a distance between two fuzzy numbers in [45], where $A,B\in {{F}_{0}}({\mathbb {R}})$, and ${{d}_{H}}$ is a Hausdorff distance. A conclusion is also given that $\left( {{F}_{0}}({\mathbb {R}}),D\right)$ constitutes a complete metric space. According the definition of general fuzzy number cut set, for any $\alpha \in (0,1]$, let ${{A}_{\alpha }}=\left[ a_{\alpha }^{1},a_{\alpha }^{2}\right]$, ${{B}_{\alpha }}=\left[ b_{\alpha }^{1},b_{\alpha }^{2}\right]$, then the distance of fuzzy numbers can be further described as

$$\begin{aligned} D(A,B) = \sup _{\begin{array}{c} \alpha \in (0,1] \end{array}}\left( \left|{a_\alpha ^1 - b_\alpha ^1} \right|\vee \left|{a_\alpha ^2 - b_\alpha ^2} \right|\right) . \end{aligned}$$

(2)

Lemma 1

[15] For a given $n\in {\mathbb {N}}$, if $A,B\in F_{0}^{tn}({\mathbb {R}})$, where $A=\left( a_{0}^{1},a_{1}^{1},\ldots ,a_{n}^{1},a_{n}^{2},\ldots ,a_{1}^{2},a_{0}^{2}\right)$, $B=\big (b_{0}^{1},b_{1}^{1},\ldots ,b_{n}^{1},b_{n}^{2},\ldots ,b_{1}^{2},b_{0}^{2}\big )$, then the distance of n-polygonal fuzzy numbers can be reduced to

$$\begin{aligned} D(A,B) = \sup _{\begin{array}{c} 0\le i\le n \end{array}}\left( \left|{a_i ^1 - b_i ^1} \right|\vee \left|{a_i ^2 - b_i ^2} \right|\right) , \end{aligned}$$

and $A\subset B$ if and only if $b_{i}^{1}\le a_{i}^{1}\le a_{i}^{2}\le b_{i}^{2}$, $i=0,1,\ldots ,n$.

According to Refs. [15, 16], it is not difficult to obtain

$$\begin{aligned}&{{Z}_{n}}(A)(x)\rightarrow A(x)~(n\rightarrow \infty ) \text { if and only if }\\&\quad \underset{n\rightarrow \infty }{\mathop {\lim }}D\left( {{Z}_{n}}(A),A \right) =0. \end{aligned}$$

Remark 2

It is obvious that the arithmetic operations defined in space $F_{0}^{tn}({\mathbb {R}})$ do not depend on Zadeh’s extension principle. More importantly, these arithmetic operations are closed and satisfy properties of linearization operations. This not only overcomes the shortcoming of Zadeh’s extension principle-based arithmetic operations, but also makes the related operations easy and intuitive. This is the key point of introducing the concept of n-PFNs.

Convergence of the neural network

Modeling of single hidden layer neural network

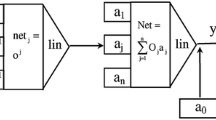
In this work, a single hidden layer feedforward neural network by using an ordered representation and arithmetic operation of n-PFNs will be established. To do this, the topology of the single hidden layer feedforward neural network model is given firstly in the following figure (Fig. 8).

Fig. 8

Topological structure diagram of single hidden layer feedforward neural network

In the network, the input and output neurons are linear, and activation function of hidden layer neurons is nonlinear. In Fig. 8, the X denotes input signal, O denotes output signal, p denotes the total number of neurons in the hidden layer, ${{U}_{j}}$ and ${{V}_{j}}$ are connection weights, and ${{\Theta }_{j}}$ are thresholds of activation function $\sigma (\cdot )$ of the hidden layer neurons, $j=1,2,\ldots ,p$. Then the input output expression of the single hidden layer feedforward neural network has the following form,

$$\begin{aligned} O(X)=\sum \limits _{j=1}^{p}{{{V}_{j}}\cdot \sigma \left( {{U}_{j}}\cdot X+{{\Theta }_{j}}\right) }, \end{aligned}$$

(3)

where $\sigma (\cdot )$ is the activation function of hidden layer neurons.

Remark 3

For a given continuous function f on compact set $K\subset {\mathbb {R}}$, define the norm of f as $\Vert f \Vert ={{\sup }_{x\in K}}|f(x) |$. Let ${{E}_{n}}(f)={{\inf }_{P\in {{\Delta }_{n}}}}\Vert f-P \Vert$, where ${{\Delta }_{n}}$ denotes the set of one variable polynomials of degree n or less, then ${{E}_{n}}(f)$ is called as the best polynomial approximation of f. For the network (3), the following conclusion holds.

Lemma 2

[3] Let $f\in C(K)$, where C(K) is the set of continuous functions on compact set K. If function $\sigma (\cdot )$ has $n+1$-order continuous derivative in ${\mathbb {R}}$, and there is a real number ${{x}_{0}}\in {\mathbb {R}}$ satisfies ${{\sigma }^{(k)}}({{x}_{0}})\ne 0$, $k=0,1,\ldots ,n$, then there must be a single hidden layer feedforward neural network $O(x)=\sum \nolimits _{j=0}^{p}{{{V}_{j}}\cdot \sigma \left( {{U}_{j}}\cdot x+{{\Theta }_{j}} \right) }$ holds $\Vert O-f \Vert \le 2{{E}_{n}}\left( f \right)$, where the number of neurons in hidden layer of the network is $n+1$.

Lemma 3

(Weierstrass approximation theorem) Let $f\in C[a,b]$. Then, for any $\varepsilon >0$, there is a Bernstein polynomial of degree n holds $\left|{{B}_{n}}\left( x \right) -f(x) \right|<\varepsilon$, for arbitrary $x\in [a,b]$, where the Bernstein polynomial has the form as ${{B}_{n}}\left( x \right) =\sum \nolimits _{k=0}^{n}{f(\frac{k}{n})C_{n}^{k}{{x}^{k}}{{\left( 1-x \right) }^{n-k}}}$.

Definition 4

A mapping $F:D\rightarrow F_{0}^{tn}({\mathbb {R}})$ is called an n-polygonal fuzzy valued function, if $F(x)=( f_{0}^{1}(x),f_{1}^{1}(x),\ldots ,f_{n}^{1}(x),f_{n}^{2}(x),\ldots ,f_{1}^{2}(x),f_{0}^{2}(x))\in F_{0}^{tn}({\mathbb {R}})$, for arbitrary $x\in D\subset {\mathbb {R}}$, where $f_{i}^{q}:D\rightarrow {\mathbb {R}}$ are continuous functions, $i=0,1,\ldots ,n$; $q=1,2$. A mapping $F:F_{0}^{tn}({\mathbb {R}})\rightarrow F_{0}^{tn}({\mathbb {R}})$ is called a generalized n-polygonal fuzzy valued function, if

$$\begin{aligned} F(X)= & {} \Big ( f_{0}^{1}(X),f_{1}^{1}(X),\ldots ,f_{n}^{1}(X),f_{n}^{2}(X),\\&\quad \ldots ,f_{1}^{2}(X),f_{0}^{2}(X)\Big ) \in F_{0}^{tn}({\mathbb {R}}), \\ \text { for any }&X\in F_{0}^{tn}({\mathbb {R}}). \end{aligned}$$

Hence, according to Definition 4 an n-PFN can be obtained from a real number or an n-PFN by special mapping.

The main objective of this section is to establish an n-polygonal fuzzy numbers based neural network to approximate an n-polygonal fuzzy valued function or generalized n-polygonal fuzzy valued function. After training, the network output can be used instead of an unknown function output, and then the reconstruction problem of unknown functions can be solved.

Convergence of polygonal fuzzy neural network (PFNN)

In this subsection, the PFNN based single hidden layer feedforward neural network model will be established to approximate a continuous n-polygonal fuzzy valued function or generalized n-polygonal fuzzy valued function. In the network, connection weights ${{U}_{j}}$, ${{V}_{j}}$ and threshold ${{\Theta }_{j}}$ are all n-PFNs, and the activation function of the hidden layer neurons $\sigma (\cdot )$ is continuous and monotonically increasing. Thus this class of networks are called as polygonal fuzzy neural networks. According to the operation characteristics of n-PFNs, the PFNN not only has stronger learning ability and fuzzy information processing ability but also are easy to construct and implement. The topology structure of the PFNN is consistent with Fig. 8.

It should be pointed out that the input of PFNN can be real number or n-PFN. Without losing generality, we only consider the case of network input is real number in the following discussion. When the network input is n-PFN, corresponding conclusion can be deduced similarly.

For the convenience of discussion, we assume that the ordered representation of connection weights and threshold are as follows,

$$\begin{aligned} \left\{ \begin{array}{lllll} {\begin{aligned} {{U}_{j}}&{}=\left( u_{0}^{1}(j),u_{1}^{1}(j),\ldots ,u_{n}^{1}(j),u_{n}^{2}(j),\ldots ,u_{1}^{2}(j),u_{0}^{2}(j) \right) , \\ {{V}_{j}}&{}=\left( v_{0}^{1}(j),v_{1}^{1}(j),\ldots ,v_{n}^{1}(j),v_{n}^{2}(j),\ldots ,v_{1}^{2}(j),v_{0}^{2}(j) \right) , \\ {{\Theta }_{j}}&{}=\Big (\theta _{0}^{1}(j),\theta _{1}^{1}(j),\ldots ,\theta _{n}^{1}(j),\theta _{n}^{2}(j),\ldots ,\theta _{1}^{2}(j),\theta _{0}^{2}(j) \Big ), \\ ~j&{}=1,2,\ldots ,p. \end{aligned}} \end{array} \right. \end{aligned}$$

(4)

Related operations involved in Eq. 3 are subject to Definition 2. In fact, the structure of PFNN is an operation system of addition and multiplication of n-PFNs, and fuzzy information is processed by ordered real numbers.

Definition 5

Let $Q\subset {\mathbb {R}}$, $F:Q\rightarrow F_{0}^{tn}({\mathbb {R}})$ be a continuous n-polygonal fuzzy valued function, and $K\subset Q$ is a compact set. For arbitrary $\varepsilon >0$, there is $p\in {\mathbb {N}}$ and ${{U}_{j}},{{V}_{j}},{{\Theta }_{j}}\in F_{0}^{tn}({\mathbb {R}})$, $j=1,2,\ldots ,p$, such that $D\left( F(x),O(x)\right) <\varepsilon$, for any $x\in K$, where O(x) is the output of a PFNN of the form Eq. (3), then O(x) is said to have approximation to function F(x).

Lemma 4

[15] Let F(x) be a continuous n-polygonal fuzzy valued function on Q, and $Q\subset {\mathbb {R}}$. Then F(x) can be expressed in the form of Eq. (3) if and only if

$$\begin{aligned}&F(x)=\left( F_{0}^{1}(x),F_{1}^{1}(x),\ldots ,F_{n}^{1}(x),F_{n}^{2}(x),\ldots ,F_{1}^{2}(x),F_{0}^{2}(x) \right) , \\&\qquad \qquad \qquad \text { for any }x\in Q, \end{aligned}$$

where $F_{i}^{q}(x)=\sum \nolimits _{j=1}^{p}{v_{i}^{q}(j)\cdot \sigma \left( u_{i}^{q}(j)\cdot x+\theta _{i}^{q}(j) \right) }$, $u_{i}^{q}(j)$, $v_{i}^{q}(j)$ and $\theta _{i}^{q}(j)$ are adjustable parameters, $i=0,1,\ldots ,n$; $q=1,2$.

If the adjustment parameters $u_{i}^{q}(j)$, $v_{i}^{q}(j)$ and $\theta _{i}^{q}(j)$ satisfy the conditions (1)-(4) of Theorem 1 given in [15], by letting $h_{i}^{q}(j)(x)=v_{i}^{q}(j)\cdot \sigma \left( u_{i}^{q}(j)\cdot x+\theta _{i}^{q}(j) \right)$, then $F_{i}^{q}(x)$ can be simplified as $F_{i}^{q}(x)=\sum \nolimits _{j=1}^{p}{h_{i}^{q}(j)(x)}$, and $h_{i}^{q}(j)(x)$ satisfy $h_{i}^{1}(j)(x)\le h_{i+1}^{1}(j)(x)\le h_{i+1}^{2}(j)(x)\le h_{i}^{2}(j)(x)$, $i=0,1,\ldots ,n-1$; $j=1,2,\ldots ,p$.

Theorem 1

Let f(x) be a continuous function on compact set K ($K\subset {\mathbb {R}}$). Then there must be a closed interval $[a,b]\subset {\mathbb {R}}$ and a continuous function ${\hat{f}}(x)$ on [a, b] hold $K\subset [a,b]$ and $f(x)={\hat{f}}(x)$, for arbitrary $x\in K$.

Proof

Because K is a compact set in ${\mathbb {R}}$, then K is bounded. Thus there must be a closed interval [a, b] holds $K\subset [a,b]$.

On the other hand, K is a bounded closed set in ${\mathbb {R}}$, then ${\mathbb {R}}-K$ is an open set. According to construction theorem of open set, there must be a family of disjoint open intervals $\left\{ ({{a}_{n}},{{b}_{n}})\right\}$ ($n=1,2,...$) satisfy ${\mathbb {R}}-K=\bigcup \nolimits _{n=1}^{+\infty }{({{a}_{n}},{{b}_{n}})}$.

According to extension theorem of continuous function on closed set, a continuous function f(x) on compact set K can be extended to a continuous function ${\hat{f}}(x)$ on ${\mathbb {R}}$. And the function ${\hat{f}}(x)$ can be constructed as the following form,

$$\begin{aligned} {\hat{f}}(x)=\left\{ \begin{array}{ll} f(x), &{}~ x\in K, \\ f({{a}_{n}})+\frac{f({{b}_{n}})-f({{a}_{n}})}{({{b}_{n}}-{{a}_{n}})}\cdot (x-{{a}_{n}}), &{}~ x\in ({{a}_{n}},\,{{b}_{n}}), \\ f({{a}_{n}}), &{}~ x\in (-\infty ,{{a}_{n}}), \\ f({{b}_{n}}), &{}~ x\in ({{b}_{n}},+\infty ). \end{array} \right. \end{aligned}$$

It is obvious that the constructed function ${\hat{f}}(x)$ is continuous at endpoints ${{a}_{n}}$ and ${{b}_{n}}$ of each interval. That is, the extended function ${\hat{f}}(x)$ is continuous on ${\mathbb {R}}$, and satisfies ${\hat{f}}(x)=f(x)$, for arbitrary $x\in K$. $\square$

Theorem 2

Let F(x) be a continuous n-polygonal fuzzy valued function on compact set K, $K\subset {\mathbb {R}}$. If monotonically increasing function $\sigma (x)$ has $n+1$-order continuous derivative on ${\mathbb {R}}$, and there is a point ${{x}_{0}}\in {\mathbb {R}}$ satisfies ${{\sigma }^{(k)}}({{x}_{0}})\ne 0$, $k=0,1,\ldots ,n$. Then, for any $\varepsilon >0$, there is a single hidden layer feedforward PFNN of the form (3), such that $D(F(x),O(x))<\varepsilon$, for any $x\in K$, where $O(x)=\left( o_{0}^{1}(x),o_{1}^{1}(x),\ldots ,o_{n}^{1}(x),o_{n}^{2}(x),\ldots ,o_{1}^{2}(x),o_{0}^{2}(x)\right)$, $o_{i}^{q}(x)=\sum \nolimits _{j=1}^{p}{v_{i}^{q}(j)\cdot \sigma \left( u_{i}^{q}(j)\cdot x+\theta _{i}^{q}(j) \right) }$, where $i=0,1,\ldots ,n$; $q=1,2$.

Proof

According to the known conditions and Definition 4, it can be obtained that the continuous n-polygonal fuzzy value function F(x) can be expressed as

$$\begin{aligned} \begin{aligned}&F(x)=\Big (f_{0}^{1}(x),f_{1}^{1}(x),\ldots ,f_{n}^{1}(x),f_{n}^{2}(x),\\&\qquad \qquad \ldots ,f_{1}^{2}(x),f_{0}^{2}(x)\Big )\in F_{0}^{tn}({\mathbb {R}}), \\&\text { for any } x\in K, \end{aligned} \end{aligned}$$

where each $f_{i}^{q}(x)$ are continuous functions on K, $i=0,1,\ldots ,n$; $q=1,2$, and satisfies

$$\begin{aligned}&f_{i}^{1}(x)\le f_{i+1}^{1}(x)\le f_{i+1}^{2}(x)\le f_{i}^{2}(x),\\&i=0,1,2,\cdots ,n-1. \end{aligned}$$

According to Theorem 1, for each continuous function $f_{i}^{q}(x)$ on $K\subset {\mathbb {R}}$, there must be a closed interval $\left[ a_{i}^{q},b_{i}^{q}\right]$ and a continuous function ${\hat{f}}_{i}^{q}(x)$ on $\left[ a_{i}^{q},b_{i}^{q}\right]$, which satisfy $K\subset \left[ a_{i}^{q},b_{i}^{q}\right]$ and ${\hat{f}}_{i}^{q}(x)=f_{i}^{q}(x)$, for any $x\in K$, $i=0,1,\ldots ,n$; $q=1,2$.

As $K\subset \left[ a_{i}^{q},b_{i}^{q}\right]$, $i=0,1,\ldots ,n$; $q=1,2$, then $K\subset \bigcap \nolimits _{i=0}^{n}{\left[ a_{i}^{q},b_{i}^{q}\right] }$, and $\bigcap \nolimits _{i=0}^{n}{\left[ a_{i}^{q},b_{i}^{q}\right] }$ is a nonempty closed interval. Let $[a,b]=\bigcap \nolimits _{i=0}^{n}{\left[ a_{i}^{q},b_{i}^{q}\right] }$, clearly, $K\subset [a,b]$. Since each ${\hat{f}}_{i}^{q}(x)$ is continuous on the compact set [a, b], and the activation function $\sigma (\cdot )$ has $n+1$-order continuous derivative. Form Lemma 2, there must be a single hidden layer feedforward neural network $o_{i}^{q}$ as

$$\begin{aligned}&o_{i}^{q}(x)=\sum \nolimits _{j=1}^{p}{v_{i}^{q}(j)\cdot \sigma \left( u_{i}^{q}(j)\cdot x+\theta _{i}^{q}(j) \right) },\\&~\text {for any } x\in [a,b], \end{aligned}$$

such that

$$\begin{aligned} \left\| {\hat{f}}_{i}^{q}-o_{i}^{q} \right\| \le 2{{E}_{n}}({\hat{f}}_{i}^{q}),~i=0,1,\ldots ,n;~q=1,2. \end{aligned}$$

(5)

where $v_{i}^{q}(j)$ and $u_{i}^{q}(j)$ are connection weights and $\theta _{i}^{q}(j)$ is threshold.

By Lemma 3, each continuous function ${\hat{f}}_{i}^{q}(x)$ on [a, b], for arbitrary $\varepsilon >0$, there must be a Bernstein polynomial ${{B}_{n}}({\hat{f}}_{i}^{q},x)$ satisfies

$$\begin{aligned} \begin{aligned} \left|{\hat{f}}_{i}^{q}(x)-{{B}_{n}}({\hat{f}}_{i}^{q},x) \right|&=\left|{\hat{f}}_{i}^{q}(x)-\sum \limits _{k=0}^{n}{{\hat{f}}_{i}^{q}\left( \tfrac{k}{n} \right) C_{n}^{k}{{x}^{k}}{{\left( 1-x \right) }^{n-k}}} \right|\\&<\varepsilon , \text { for all } x\in [a,b]. \end{aligned} \end{aligned}$$

According to Formula (5), the best polynomial approximation of each expansion function ${\hat{f}}_{i}^{q}(x)$ on [a, b] must satisfy

$$\begin{aligned}\begin{aligned} {{E}_{n}}({\hat{f}}_{i}^{q})&={{\inf }_{P\in {{\Delta }_{n}}}}\left\| {\hat{f}}_{i}^{q}-P \right\| \le \left\| {\hat{f}}_{i}^{q}-{{B}_{n}}({\hat{f}}_{i}^{q}) \right\| \\&=\underset{x\in [a,b]}{\mathop {\sup }}\left|{\hat{f}}_{i}^{q}(x)-{{B}_{n}}({\hat{f}}_{i}^{q},x) \right|<\varepsilon . \end{aligned}\end{aligned}$$

Therefore, for all $x\in [a,b]$, it can be obtained that

$$\begin{aligned} \left\| {\hat{f}}_{i}^{q}-o_{i}^{q} \right\| <2\varepsilon ,~ i=0,1,\ldots ,n;~q=1,2. \end{aligned}$$

And then according to the compact set $K\subset [a,b]$, for any $x\in K$, there must be

$$\begin{aligned} \left|f_{i}^{q}(x)-o_{i}^{q}(x)\right|=\left|{\hat{f}}_{i}^{q}(x)-o_{i}^{q}(x)\right|\le \left|{\hat{f}}_{i}^{q}-o_{i}^{q} \right|<2\varepsilon . \end{aligned}$$

(6)

That is to say,

$$\begin{aligned}&f_{i}^{q}(x)-2\varepsilon<o_{i}^{q}(x)<f_{i}^{q}(x)+2\varepsilon ,\\&~i=0,1,\ldots ,n;~q=1,2. \end{aligned}$$

In particular, when $q=1,2$, it is obvious that

$$\begin{aligned} \begin{aligned}&f_{i}^{1}(x)-2\varepsilon<\underline{o_{i}^{1}(x)<f_{i}^{1}(x)+2\varepsilon },~~\\&\quad \underline{f_{i+1}^{1}(x)-2\varepsilon<o_{i+1}^{1}(x)}<f_{i+1}^{1}(x)+2\varepsilon ; \\&\underline{f_{i}^{2}(x)-2\varepsilon<o_{i}^{2}(x)}<f_{i}^{2}(x)+2\varepsilon , \\&\quad f_{i+1}^{2}(x)-2\varepsilon<\underline{o_{i+1}^{2}(x)<f_{i+1}^{2}(x)+2\varepsilon }. \end{aligned} \end{aligned}$$

According to the above line drawing inequality, is can be easily got that

$$\begin{aligned}\begin{aligned}&o_{i+1}^{1}(x)-o_{i}^{1}(x)>f_{i+1}^{1}(x)-f_{i}^{1}(x)-4\varepsilon ,\\&o_{i+1}^{2}(x)-o_{i}^{2}(x)<f_{i+1}^{2}(x)-f_{i}^{2}(x)+4\varepsilon . \end{aligned}\end{aligned}$$

Form the arbitrariness of $\varepsilon$, for any $x\in K$, we immediately obtain that

$$\begin{aligned} \begin{aligned}&o_{i+1}^{1}(x)-o_{i}^{1}(x)\ge f_{i+1}^{1}(x)-f_{i}^{1}(x)\ge 0, \\&o_{i+1}^{2}(x)-o_{i}^{2}(x)\le f_{i+1}^{2}(x)-f_{i}^{2}(x)\le 0. \end{aligned}\end{aligned}$$

Therefore, we can also obtained that

$$\begin{aligned}&o_{i}^{1}(x)\le o_{i+1}^{1}(x)\le o_{i+1}^{2}(x) \le o_{i}^{2}(x), \\&i=0,1,2,\ldots ,n-1. \end{aligned}$$

Let

$$\begin{aligned} O(x)=\left( o_{0}^{1}(x),o_{1}^{1}(x),\ldots ,o_{n}^{1}(x),o_{n}^{2}(x),\ldots ,o_{1}^{2}(x),o_{0}^{2}(x) \right) , \end{aligned}$$

then O(x) is an ordered representation of n-polygonal fuzzy value function. In other words, there is a single hidden layer feedforward PFNN in the form of Eq. (3), where

$$\begin{aligned}&o_{i}^{q}(x)=\sum \nolimits _{j=1}^{p}{v_{i}^{q}(j)\cdot }{\sigma \left( u_{i}^{q}(j)\cdot x+\theta _{i}^{q}(j) \right) },\\&~i=0,1,\ldots ,n; ~q=1,2. \end{aligned}$$

By Ref. [15], the parameters $u_{i}^{q}(j)$, $v_{i}^{q}(j)$ and $\theta _{i}^{q}(j)$ of each function $o_{i}^{q}(x)$ ($i=0,1,\ldots ,n$; $q=1,2$) can be adjusted appropriately to satisfy the conditions (1)-(4) of Theorem 1 in [15]. If necessary, enough supplementary terms can be added [15, 17, 23].

According to Lemma 1 and Formula (6), it is not difficult to obtain that

$$\begin{aligned} \begin{aligned} D\left( F(x),O(x)\right)&= \underset{0\le i\le n}{\mathop {\sup }}\left( \left|f_{i}^{1}(x)-o_{i}^{1}(x)\right|\vee \left|f_{i}^{2}(x)-o_{i}^{2}(x)\right|\right) \\&< \underset{0\le i\le n}{\mathop {\sup }}(2\varepsilon \vee 2\varepsilon ) = 2\varepsilon . \end{aligned} \end{aligned}$$

Therefore, a single hidden layer feedforward fuzzy neural network (3) can approach the continuous n-polygonal fuzzy value function F(x).

So far, with the help of Weierstrass approximation theorem, the convergence of a single hidden layer feedforward PFNN is proved under the conditions of an activation function satisfies certain conditions, which the network can approximate to a continuous n-polygonal fuzzy valued function is explained. This provides a theoretical basis for further application of the network to mathematical modeling of continuous fuzzy systems. $\square$

Remark 4

In this subsection, an approach for a PFNN to approximate a continuous n-polygonal fuzzy valued function is presented. For a continuous generalized n-polygonal fuzzy valued function, a PFNN can be constructed in the same way. The related operations involved are completely consistent, and only need to expand the network input from real number to n-PFN. This is also the main purpose of this paper to establish a single hidden layer neural network based on the ordered representation of n-polygonal fuzzy numbers.

Gradient descent algorithm

Although the structure of feedforward fuzzy neural network is simple, it shows many advantages in dealing with uncertain problems. It can not only approximate any continuous function and square integrable function with arbitrary accuracy, but also accurately realize any finite training sample set, it is a kind of static nonlinear mapping. However, the feedforward network also has some problems to be solved urgently, such as the optimization of network structure, the design of learning algorithm, the improvement of convergence speed and error accuracy. One of the main reasons for these defects is that the adjustment parameters (fuzzy numbers) of feedforward fuzzy neural network does not meet the linear operation, resulting in that most feedforward networks are learning networks, Due to the lack of certain dynamic behavior, its classification ability and pattern recognition ability are generally weak. In addition, BP algorithm is a local search optimization method. Its weight is gradually adjusted along the direction of local improvement, which usually makes the algorithm fall into local extremum, and the weight converges to a local minimum, and even leads to network training failure, such as many training times, low learning efficiency, slow convergence speed, etc. Therefore, it is an urgent problem to find a basic tool that can better describe fuzzy information and meet linear operations to expand the feedforward fuzzy neural network and backpropagation (BP) network.

At present, no one uses the ordered representation of n-PFNs as a tool to study the approximation of PFNN. Although n-PFN is a special case of general fuzzy number, it can describe fuzzy information with the help of the ordered representation of finite real numbers. Its biggest advantage is that its arithmetic operations avoid the traditional Zadeh’s extension principle and approximately realizes the linearization operations. This is the main motivation for us to introduce the n-PFNs and its ordered representation. Especially, it is of great theoretical significance to utilize the n-PFNs to deal with the input and output of fuzzy information.

However, it is more important to realize the nonlinear operation between the general fuzzy numbers involved in the network. The solution of this problem is not only of great significance to realize the optimization algorithm of the neural network, but also provides a theoretical basis for the soft computing technology and application of the network. In fact, the polygonal fuzzy neural network is a new network which depends on the combination of n-polygonal fuzzy number and artificial neural network. It does not need to implement algorithm through general fuzzy number cut set, but design algorithm using the ordered representation of n-PFNs based linear operations, which can greatly simplify the process of designing and optimizing learning algorithm.

In this subsection, the feedforward PFNN with single hidden layer is studied. In the network, input variable is a real number $x\in {\mathbb {R}}$ or an n-PFN $X=(x_{0}^{1},x_{1}^{1},\ldots ,x_{n}^{1},x_{n}^{2},\ldots ,x_{1}^{2},x_{0}^{2})\in F_{0}^{tn}({\mathbb {R}})$. Input output expression of the single hidden layer feedforward PFNN is as follows:

$$\begin{aligned} O(x)=\sum \limits _{j=1}^{p}{{{V}_{j}}\cdot \sigma \left( {{U}_{j}}\cdot x+{{\Theta }_{j}} \right) }, \end{aligned}$$

(7)

or

$$\begin{aligned} O(X)=\sum \limits _{j=1}^{p}{{{V}_{j}}\cdot \sigma \left( {{U}_{j}}\cdot X+{{\Theta }_{j}} \right) }, \end{aligned}$$

(8)

where the ordered representation of the connection weights and threshold are exactly the same as Eq. (4). The activation function $\sigma$ of hidden layer neurons is monotonically increasing and differentiable everywhere.

To calculate the derivative of error function conveniently, a metric ${{D}_{E}}$ is introduced to describe the distance of n-PFNs. That is, for any $A, B\in F_{0}^{tn}({\mathbb {R}})$, and $A=\left( a_{0}^{1},a_{1}^{1},\ldots ,a_{n}^{1},a_{n}^{2},\ldots ,a_{1}^{2},a_{0}^{2} \right)$ and $B=\big ( b_{0}^{1},b_{1}^{1},\ldots ,b_{n}^{1},b_{n}^{2},\ldots ,b_{1}^{2},b_{0}^{2} \big )$, let

$$\begin{aligned} {{D}_{E}}(A,B)=\sqrt{\sum \limits _{i=0}^{n}{\left( {{\left( a_{i}^{1}-b_{i}^{1} \right) }^{2}}+{{\left( a_{i}^{2}-b_{i}^{2} \right) }^{2}} \right) }}.\end{aligned}$$

Obviously, it is not difficult to verify that ${{D}_{E}}$ is a metric (distance). For the sake of unity in discussion, it is assumed that inputs and outputs of the neural network are all n-PFNs, that is the input space and the output space are all $F_{0}^{tn}({\mathbb {R}})$. It needs to be pointed out that the following discussion is valid when the input space is ${\mathbb {R}}$. In fact, for a real number $x\in {\mathbb {R}}$, if define $X=(x,x,\ldots ,x,x,\ldots ,x,x)\in F_{0}^{tn}({\mathbb {R}})$, then $x\in {\mathbb {R}}$ can be seen as a special case of $X\in F_{0}^{tn}({\mathbb {R}})$. Thus in the following, we only take the input $X\in F_{0}^{tn}({\mathbb {R}})$ as the representative to discuss.

Let $\left( X(k);Y(k) \right)$ be k groups of n-PFNs pattern pairs for neural network (8) training, $k=1,2,\ldots ,K$, where $X(k), Y(k)\in F_{0}^{tn}({\mathbb {R}})$, and X(k) is the input of the k-th pattern pair of the network, and Y(k) is the expected output corresponding to X(k). The output of the network corresponding to input X(k) is denoted by O(k), that is the conditions $O(k)=O\left( X(k)\right)$ are satisfied for the network, $k=1,2,\ldots ,K$. For the convenience of discussion, the network inputs, expected outputs and network output are shown in detail as follows:

$$\begin{aligned}\left\{ \begin{array}{lllll} {\begin{aligned} &{}X(k)=\left( x_{0}^{1}(k),x_{1}^{1}(k),\ldots ,x_{n}^{1}(k),x_{n}^{2}(k),\ldots ,x_{1}^{2}(k),x_{0}^{2}(k) \right) , \\ &{}Y(k)=\left( y_{0}^{1}(k),y_{1}^{1}(k),\ldots ,y_{n}^{1}(k),y_{n}^{2}(k),\ldots ,y_{1}^{2}(k),y_{0}^{2}(k) \right) , \\ &{}O(k)=\Big (o_{0}^{1}(k),\ o_{1}^{1}(k),\ldots ,o_{n}^{1}(k),o_{n}^{2}(k), \ldots ,o_{1}^{2}(k),\ o_{0}^{2}(k) \Big ),\\ &{}k=1,2,\ldots ,K. \end{aligned}}\end{array} \right. \end{aligned}$$

For a single hidden layer feedforward PFNN O(X), the error function is defined as

$$\begin{aligned} \begin{aligned} E\left( O(X)\right)&=\frac{1}{2K}\sum \limits _{k=1}^{K}{{{D}_{E}}{{\left( O(k),Y(k)\right) }^{2}}} \\&=\frac{1}{2K}\sum \limits _{k=1}^{K}{\left( \sum \limits _{i=0}^{n}{\left( {{\left( o_{i}^{1}(k)-y_{i}^{1}(k)\right) }^{2}} +{{\left( o_{i}^{2}(k)-y_{i}^{2}(k)\right) }^{2}}\right) }\right) }. \end{aligned} \end{aligned}$$

(9)

In fact, the structural expression of PFNN shown in Eqs. (7) and (8) are operation systems of the addition and multiplication of n-PFNs. According to the definition of ordered representation, each n-PFN is uniquely determined by $2n+2$ ordered real numbers. Hence, the connection weights ${{U}_{j}}$, ${{V}_{j}}$, and threshold ${{\Theta }_{j}}$ can be adjusted continuously to make the network output close to the expected output. For the unity of expression, the adjustable parameters $u_{i}^{q}(j)$, $v_{i}^{q}(j)$ and $\theta _{i}^{q}(j)$ ($i=0,1,\ldots ,n$; $j=1,2,\ldots ,p$; $q=1,2$) of the networks (7) and (8) are integrated into a high dimensional parameter vector, that is,

$$\begin{aligned}\begin{aligned} W=&\left( u_{0}^{1}(1),u_{1}^{1}(1),\ldots ,u_{n}^{1}(1),u_{n}^{2}(1),\ldots ,u_{1}^{2}(1),u_{0}^{2}(1),\ldots ,\right. \\&~~u_{0}^{1}(p),u_{1}^{1}(p),\ldots ,u_{n}^{1}(p),u_{n}^{2}(p),\ldots ,u_{1}^{2}(p),u_{0}^{2}(p), \\&~~v_{0}^{1}(1),v_{1}^{1}(1),\ldots ,v_{n}^{1}(1),v_{n}^{2}(1),\ldots ,v_{1}^{2}(1),v_{0}^{2}(1),\ldots , \\&~~v_{0}^{1}(p),v_{1}^{1}(p),\ldots ,v_{n}^{1}(p),v_{n}^{2}(p),\ldots ,v_{1}^{2}(p),v_{0}^{2}(p),\\&~~\theta _{0}^{1}(1),\theta _{1}^{1}(1),\ldots ,\theta _{n}^{1}(1),\theta _{n}^{2}(1),\ldots ,\theta _{1}^{2}(1),\theta _{0}^{2}(1),\ldots , \\&~~\theta _{0}^{1}(p),\theta _{1}^{1}(p),\ldots ,\theta _{n}^{1}(p),\theta _{n}^{2}(p),\ldots ,\left. \theta _{1}^{2}(p),\theta _{0}^{2}(p) \right) \\ \triangleq&\left( {{w}_{1}},{{w}_{2}},\ldots ,{{w}_{i}},\ldots ,{{w}_{N}} \right) , \end{aligned}\end{aligned}$$

where $N=3p\left( 2n+2 \right)$. Therefore, the error function W defined in Eq. (8) can be simply expressed as E(W) or $E\left( {{w}_{1}},{{w}_{2}},\ldots ,{{w}_{N}} \right)$.

Lemma 5

[15] Let E(W) be an error function defined by Eq. (8), then the E(W) is differentiable almost everywhere in the high dimensional space ${{{\mathbb {R}}}^{_{N}}}$, and its partial derivatives ${\partial E(W)}/{\partial {{w}_{i}}}$ exist, $i=1,2,\ldots ,N$.

For convenience, denote the gradient vector of error function E(W) as $\nabla E(W)$, that is

$$\begin{aligned}\nabla E(W)=\left( \frac{\partial E(W)}{\partial {{w}_{1}}},\frac{\partial E(W)}{\partial {{w}_{2}}},\ldots ,\frac{\partial E(W)}{\partial {{w}_{N}}} \right) .\end{aligned}$$

In the following, a gradient descent algorithm is used to adjust the parameter vector of PFNN. The algorithm program of n-polygonal fuzzy numbers based single hidden layer feedforward neural network is as follows.

Step 1 Determine the initial value of relevant parameters. Let $t=0$, $\varepsilon >0$, and $W(t)={{W}_{0}}$, where t is the iteration number, $\varepsilon$ is the iteration termination constant, and ${{W}_{0}}$ is the initial value of neural network parameter vector. The number of neurons in the network is p.

Step 2 Calculate the neural network training error $E\left( W(t) \right)$. If the Euclidean norm of $E\left( W(t) \right)$ satisfies $\left\| E\left( W(t) \right) \right\| <\varepsilon$, the iteration turns to Step 6, Otherwise goes to the next step.

Step 3 Update the neural network parameter vector as $W(t+1)=W(t)-\eta \cdot \nabla E\left( W(t) \right)$, where $\eta$ is iteration step size, and $\nabla E\left( W(t) \right)$ is the gradient vector of $E\left( W(t) \right)$.

Step 4 Calculate the neural network connection weights ${{U}_{j}}(t+1)$, ${{V}_{j}}(t+1)$ and threshold ${{\Theta }_{j}}(t+1)$, $j\in \left\{ 1,2,\ldots ,p \right\}$. If ${{U}_{j}}(t+1)$, ${{V}_{j}}(t+1)$ and ${{\Theta }_{j}}(t+1)$ do not belong to $F_{0}^{tn}({\mathbb {R}})$, then by adjusting the order of components to make them n-PFNs.

Step 5 Calculate the Euclidean norm of $E\left( W(t+1) \right)$. If the norm satisfies $\left\| E\left( W(t+1) \right) \right\| <\varepsilon$, the iteration goes to Step 6. Otherwise, let $t=t+1$, and turn to Step 3.

Step 6 Output the parameter vector $W(t+1)$.

In the above algorithm, Step 4 and Step 5 are about the design of adjustment parameters. ${{U}_{j}}(t+1)$, ${{V}_{j}}(t+1)$ and ${{\Theta }_{j}}(t+1)$ represent connection weights and threshold of hidden layer neuron j ($j=1,2,\ldots ,p$) corresponding to step $t+1$. It should be noted that these parameters must satisfy the following inequalities after adjusting element order,

$$\begin{aligned}\left\{ \begin{aligned} {{U}_{j}}(t+1):&~~ u_{0}^{1}(j)(t+1) \le \cdots \le u_{n}^{1}(j)(t+1) \\&~~~~~ \le u_{n}^{2}(j)(t+1) \le \cdots \le u_{0}^{2}(j)(t+1), \\ {{V}_{j}}(t+1):&~~ v_{0}^{1}(j)(t+1)\le \cdots \le v_{n}^{1}(j)(t+1) \\&~~~~~ \le v_{n}^{2}(j)(t+1) \le \cdots \le v_{0}^{2}(j)(t+1), \\ {{\Theta }_{j}}(t+1):&~~ \theta _{0}^{1}(j)(t+1) \le \cdots \le \theta _{n}^{1}(j)(t+1) \\&~~~~~ \le \theta _{n}^{2}(j)(t+1) \le \cdots \le \theta _{0}^{2}(j)(t+1). \end{aligned} \right. \end{aligned}$$

Remark 5

Because only the gradient information is needed, the above-mentioned gradient descent algorithm is easy to implement. Gradient descent algorithm is a common method of neural network training. To improve the efficiency of network training, some other suitable learning algorithms can be chosen, such as the Newton algorithm, quasi-Newton algorithm. In addition, fixed step size is employed in Step 3 of the given iterative algorithm, such as using variable step size can be considered further. The whole work flowchart can be shown in Fig. 9 below.

Fig. 9

Work flowchart of training and testing the PFNN approximator

In the flowchart shown in Fig. 9, it is not difficult to see that the proposed algorithm has a complete working system and operation rule. According to the construction method of the PFNN approximator given in “Gradient descent algorithm”, the structure of the network can be determined by choosing neurons and activation function of them. In addition, by the gradient descent algorithm given in this section, the PFNN approximator can be trained iteratively by using training data, so that we can test the generalization ability of the trained network.

Fig. 10

Training error curve of the PFNN approximator

Table 1 Training inputs ${{x}_{Tr}}(k)$, expected outputs ${{Y}_{Tr}}(k)$, PFNN outputs ${{O}_{Tr}}(k)$, and TNN outputs ${{{O}'}_{Tr}}(k)$

Simulation examples

Because the outputs, connection weights and thresholds of the single hidden layer neural network mentioned above are n-polygonal fuzzy numbers, it is more intuitive and simple to design a learning algorithm on $F_{0}^{tn}({\mathbb {R}})$. Hence, two fuzzy reasoning models which input spaces are ${\mathbb {R}}$ and $F_{0}^{tn}({\mathbb {R}})$ are simulated by using the presented polygonal fuzzy neural networks (PFNNs), respectively. These models can be applied to automatic control of vehicle speed or automatic operation of container crane, etc. Next, we will give two examples in the case of $n=3$ to illustrate the effectiveness of PFNN approximator. To verify the generalization ability of the trained PFNN approximator, we randomly divide the given sample data into two parts: training set and test set, that is, about 70% is used for network training and about 30% for performance testing.

Fig. 11

Training results of the two approximators: PFNN and TNN

For the following two examples, the actual practice is to randomly take 9 of the 13 samples for training and the remaining 4 for testing. In addition, for the sake of showing advantage and effectiveness of the PFNN approximator by comparison, we construct traditional neural network (TNN) based approximator using the same sample data with PFNN approximator. It should be pointed out that since the dimension of the output space ${{{\mathbb {R}}}^{2\times 3+2}}={{{\mathbb {R}}}^{8}}$ is eight, the TNN based approximators must be constructed separately to approach each output. Thus, the structure of the TNN approximator is complex. The details are in the following two examples.

Example 3

Input space is ${\mathbb {R}}$. We want to obtain a PFNN approximator of the form (7). To do this, there are 13 groups of sample pattern pairs $\left( x(m);Y(m) \right)$ be used in network training and performance testing, where x(m) and Y(m) are inputs and expected outputs of the network, respectively, $m=1,2,\ldots ,13$. In fact, these groups of sample pattern pairs come from a 3-polygonal fuzzy valued function F(x), which analytic expression is as follows,

$$\begin{aligned} \begin{aligned} F(x)&= \left( {{x}^{3}},x,{{x}^{{1}/{2}}},{{x}^{{1}/{4}}},{{(x+1)}^{{1}/{4}}},{{(x+1)}^{{1}/{2}}},{{(x+1)}^{{3}/{2}}}, \right. \\&\quad \left. {{(x+1)}^{2}} \right) ,\\&\text {for all}~ x\in [0,1]. \end{aligned} \end{aligned}$$

(10)

After randomly selecting 13 values of variable x in interval (0, 1), i.e. x(m), $m=1,2,\ldots ,13$, then the corresponding 13 values of the 3-polygonal fuzzy valued function F(x) can be obtained according to (10), i.e. Y(m), $m=1,2,\ldots ,13$. By grouping them randomly, we can obtain training set and test set, which are expressed as $\left( {{x}_{Tr}}(k);{{Y}_{Tr}}(k) \right)$ and $\left( {{x}_{Te}}(l);{{Y}_{Te}}(l) \right)$, respectively, $k=1,2,\ldots ,9$, $l=1,2,\ldots ,4$.

Table 2 Test inputs ${{x}_{Te}}(l)$, expected outputs ${{Y}_{Te}}(l)$, PFNN outputs ${{O}_{Te}}(l)$, and TNN outputs ${{{O}'}_{Te}}(l)$

Before network training, we need to determine the structure of the network. The number of neurons and the activation function of these neurons are chosen as $p=5$ and $\sigma (x)=\frac{1}{1+{{e}^{-x}}}$, respectively. The network training parameters are chosen as $\eta =0.5$ and $\varepsilon =0.01$. After doing these, a PFNN approximator can be constructed and trained.

After 3194 iterations, the training process of the PFNN is terminated. Figure 10 shows the change of training error with the increase of iteration times. It can be seen that the training error decreases gradually with the increase of the iteration times.

Remark 6

It should be pointed out that the network training speed is related to the number of neurons p, activation function $\sigma (\cdot )$ and iteration parameters $\eta$, $\varepsilon$, etc. In addition, it can be seen that the training algorithm converges faster in early stage and slower in a later stage. By improving algorithm, the overall convergence efficiency may be improved.

The specific input and expected output data used for the PFNN approximator training is given in Table 1 below (see the second and third columns of the table). The actual output data of the PFNN approximator is shown in the fourth column of Table 1. To give numerical comparison results, outputs of the TNN approximator are shown in the fifth column of Table 1.

In addition, to intuitively show the training performance of the PFNN approximator and the TNN approximator, images of these 3-PFNs are given in Fig. 11.

Clearly, it is not difficult to see from Fig. 11 that the training outputs of the PFNN approximator and the TNN approximator can approach the expected outputs well.

In the following, we will verify the generalization ability of the trained PFNN approximator and compare it with the trained TNN approximators. We input ${{x}_{Te}}(l)$ into the trained PFNN approximator, and then the corresponding test outputs ${{O}_{Te}}(l)$ can be obtained, $l=1,2,\ldots ,4$. See the fourth column of Table 2 for specific data. To compare test results, the expected outputs and the test outputs of the TNN approximator are also given in Table 2, where ${{Y}_{Te}}(l)$ is the expected outputs and ${{{O}'}_{Te}}(l)$ the TNN outputs, $l=1,2,\ldots ,4$.

In addition, in order to intuitively give the comparison of the test results, images of the outputs, that are ${{Y}_{Te}}(l)$, ${{O}_{Te}}(l)$, and ${{{O}'}_{Te}}(l)$, $l=1,2,\ldots ,4$, are shown in Fig. 12.

Fig. 12

Test results of the two approximators: PFNN and TNN

We can see from Fig. 12 that the test outputs of the PFNN approximator and the TNN approximator can approach the expected outputs well.

Next, we will numerically analyze distances between outputs of approximators and expected outputs to verify the performance of the PFNN and TNN. Since these outputs are all 3-PFNs, we use the distance of 3-PFNs given in Lemma 1 for numerical analysis. It is easy to understand that the smaller the distance values, the stronger the approximation ability of the network.

For convenience, let O(m) be outputs of PFNN approximator corresponding to x(m), and ${O}'(m)$ outputs of the TNN approximator, $m=1,2,\ldots ,13$. According to Tables 1 and 2, the distance data shown in Table 3 can be obtained, where $D\left( Y(m),O(m) \right)$ and $D\left( Y(m),{O}'(m) \right)$ are the distances in the sense of Lemma 1, $m=1,2,\ldots ,13$.

Table 3 Distances between outputs of approximators and expected outputs

To compare the performance of the PFNN approximator and the TNN approximator, According to Table 3, the scatter plots of these distance data are given in Fig. 13 as follows:

Fig. 13

Scatter plot of distances

Table 4 Training inputs ${{X}_{Tr}}(k)$, expected outputs ${{Y}_{Tr}}(k)$, PFNN outputs ${{O}_{Tr}}(k)$, and TNN outputs ${{{O}'}_{Tr}}(k)$

Remark 7

It should be pointed out that generally speaking, the approximation effect of the PFNN and the TNN can be further improved by increasing the number of neurons p or decreasing the value of iteration parameter $\varepsilon$, etc.

Example 4

Input space is $F_{0}^{tn}({\mathbb {R}})$. We want to obtain a PFNN approximator of the form (8). To do this, there are 13 groups of sample pattern pairs $\left( X(m);Y(m) \right)$ be used in network training and performance test, where X(m) and Y(m) are inputs and expected outputs of the network, respectively, $m=1,2,\ldots ,13$. In fact, these groups of sample pattern pairs come from a 3-polygonal fuzzy valued function $F:F_{0}^{t3}({\mathbb {R}})\rightarrow F_{0}^{t3}({\mathbb {R}})$, which analytic expression is given as follows. For all $x\in [0,1]$,

$$\begin{aligned} X= & {} \left( {{x}^{3}},x,{{x}^{\frac{1}{2}}},{{x}^{\frac{1}{4}}},{{(x+1)}^{\frac{1}{4}}},{{(x+1)}^{\frac{1}{2}}}, \nonumber \right. \\&\left. {{(x+1)}^{\frac{3}{2}}},{{(x+1)}^{2}} \right) \in F_{0}^{tn}({\mathbb {R}}), \end{aligned}$$

(11)

$$\begin{aligned} F(X)= & {} \left( {{x}^{4}},{{x}^{\frac{3}{2}}},x,{{x}^{\frac{1}{4}}}{{(x+1)}^{\frac{1}{4}}},{{(x+1)}^{\frac{1}{2}}}, \nonumber \right. \\&\left. {{x}^{2}}+x+1,{{(x+1)}^{2}},{{(x+1)}^{3}} \right) . \end{aligned}$$

(12)

After randomly selecting 13 values of variable x in interval (0, 1), then inputs and outputs of sample pattern pairs X(m) and Y(m) can be obtained according to (11) and (12), respectively, $m=1,2,\ldots ,13$. Then after random grouping, there are 9 groups of sample pattern pairs in training set and 4 groups of sample pattern pairs in test set. Let $\left( {{X}_{Tr}}(k);{{Y}_{Tr}}(k)\right)$ represent the training set, and $\left( {{X}_{Te}}(l);{{Y}_{Te}}(l) \right)$ the test set, $k=1,2,\ldots ,9$, $l=1,2,\ldots ,4$.

We determine the structure of the network which has the form of (8) as follows: the number of neurons is $p=4$, and activation function of neurons is $\sigma (x)=\frac{1}{1+{{e}^{-x}}}$. Parameters used for the PFNN training are chosen as $\eta =0.2$ and $\varepsilon =0.1$, respectively. The specific data of input and output used for approximator training is given in Table 4 (See the second and third columns of the table for details).

After 3423 iterations, training process of the PFNN is terminated. Figure 14 shows the change of training error with the increase of iteration times, that is, the training error decreases gradually with the increase of the iteration times.

Fig. 14

Training error curve of the PFNN approximator

From Figs. 10 and 14, it can be seen that the training error decreases gradually with the increase of the number of iterations. Especially in the initial stage of iteration, the error decreases very fast. It shows that the gradient descent algorithm given in “Gradient descent algorithm” is effective.

Similar to Example 3, we use the same training set to construct a TNN approximator and compare its performance with the PFNN approximator. The training outputs of the two approximators are also given in Table 4, where ${{O}_{Tr}}(k)$ for the PFNN approximator and ${{{O}'}_{Tr}}(k)$ for the TNN approximator, $k=1,2,\ldots ,9$.

In addition, to intuitively show the training performance of the two approximators, Fig. 15 gives the images of these outputs. We can see that the training outputs of the PFNN approximator and the TNN approximator approach the expected outputs well.

Fig. 15

Training results of the two approximators: PFNN and TNN

From Figs. 11 and 15, it can be seen that the training outputs of the PFNN approximator are close to the expected outputs. It shows that the proposed methods of PFNN approximator constructing and training in “Convergence of the neural network” and “Gradient descent algorithm” are effective.

Table 5 Test inputs ${{X}_{Te}}(l)$, expected outputs ${{Y}_{Te}}(l)$, PFNN outputs ${{O}_{Te}}(l)$, and TNN outputs ${{{O}'}_{Te}}(l)$

Fig. 16

Test results of the two approximators: PFNN and TNN

Then, we test the generalization ability of the two approximators with the test inputs ${{X}_{Te}}(l)$, $l=1,2,\ldots ,4$, and compare the output results. The test inputs, expected outputs, and the outputs of the two approximators are given in Table 5, where ${{Y}_{Te}}(l)$ are the expected outputs, ${{O}_{Te}}(l)$ the outputs of PFNN approximator, and ${{{O}'}_{Te}}(l)$ the outputs of the TNN approximator, $l=1,2,\ldots ,4$.

According to Table 5, the test results of the PFNN approximator and the TNN approximator are shown in Fig. 16. We can see that the test outputs of the PFNN approximator and the TNN approximator can approach the expected outputs well.

From Figs. 12 and 16, it can be seen that the test outputs of the PFNN approximator are close to the expected outputs, i.e. that the trained PFNN approximator has good generalization ability. This further shows the effectiveness of the proposed PFNN constructing approach.

Let O(m) be outputs of the PFNN approximator corresponding to the input X(m), and ${O}'(m)$ the outputs of the TNN approximator, $m=1,2,\ldots ,13$. According to Tables 4-5, the distance data can be obtained as shown in Table 6, where $D\left( Y(m),O(m) \right)$ and $D\left( Y(m),{O}'(m) \right)$ are the distances in the sense of Lemma 1, $m=1,2,\ldots ,13$.

Table 6 Distances between outputs of approximators and expected outputs

According to Table 6, the scatter plots of the distances $D\left( Y(m),O(m) \right)$ and $D\left( Y(m),{O}'(m) \right)$ are given in Fig. 17 below.

Fig. 17

Scatter plot of distances

From Figs. 13 and 17, we can conclude that after training, the PFNN can achieve the same level of approximation performance with TNN. However, it should be emphasized again that to realize the output of 3-PFNs, the TNN approximator needs eight independent neural networks to output each corresponding component, respectively. So the structure of TNN approximator is more complex. Therefore, in comparison, the PFNN approximator has the advantage of a simple structure.

By analyzing the results of the two simulation examples, we can get that the proposed PFNN approximator construction method and the gradient descent algorithm are effective. From Tables 1, 4 and Figs. 11, 15, it can be known that the proposed method of PFNN approximators constructing and training is effective. Figs. 10 and 14 show that the given gradient descent algorithm has good convergence. In addition, it can be seen from Tables 2, 5 and Figs. 12, 16 that the trained PFNN approximator have good generalization ability. Figs. 11, 12, 15, 16 and Tables 3, 6 indicate that the constructed PFNN approximator has good approximation efficiency. Therefore, the constructed polygonal fuzzy neural network based on ordered representation of n-PFNs has some advantages over the traditional neural network.

Conclusion

As a universal approximator, a neural network has the ability to learn and approximate any unknown continuous function, while fuzzy theory has a unique effect in dealing with problems with uncertainty. Fortunately, the proposed n-PFNs not only satisfies the linear operation, but also can approximately describe the general fuzzy numbers through the ordered representation of finite real numbers. Therefore, selecting n-PFNs as the adjustment parameter of feedforward fuzzy neural network can make the network form a linear mapping, so as to linearize the input and output of the constructed network. A feedforward neural network with a single hidden layer is established by Weierstrass approximation theorem under the ordered representation of n-polygonal fuzzy number. It is proved that the proposed network has the approximation to a continuous n-polygonal fuzzy value function or a generalized n-polygonal fuzzy value function. This provides a theoretical basis for the application of the fuzzy neural network with single hidden layer in a continuous system. A gradient descendent algorithm is designed by using the iterative operations of parameter vectors in n-PFNs space. The effectiveness of the network and training algorithm is verified by simulation examples. A single layer PFNN is established by the ordered representation of n-PFNs, and the method of describing fuzzy information by n-PFNs can be further extended to the construction of other fuzzy neural networks, such as the convolutional neural network and recurrent fuzzy neural network, and then explore and design some intelligent algorithms of these networks. Besides, to improve the efficiency and convergence speed of network training, the n-PFNs can be further considered to be applied to genetic algorithm or particle swarm optimization algorithm, and then the improvement of gradient descent algorithm and variable step-size method are also the focus of the next step research.