Multiobjective multitasking optimization assisted by multidirectional prediction method

Abstract

Multiobjective multitasking optimization (MTO) is an emerging research topic in the field of evolutionary computation, which has attracted extensive attention, and many evolutionary multitasking (EMT) algorithms have been proposed. One of the core issues, designing an efficient transfer strategy, has been scarcely explored. Keeping this in mind, this paper is the first attempt to design an efficient transfer strategy based on multidirectional prediction method. Specifically, the population is divided into multiple classes by the binary clustering method, and the representative point of each class is calculated. Then, an effective prediction direction method is developed to generate multiple prediction directions by representative points. Afterward, a mutation strength adaptation method is proposed according to the improvement degree of each class. Finally, the predictive transferred solutions are generated as transfer knowledge by the prediction directions and mutation strengths. By the above process, a multiobjective EMT algorithm based on multidirectional prediction method is presented. Experiments on two MTO test suits indicate that the proposed algorithm is effective and competitive to other state-of-the-art EMT algorithms.

Introduction

Evolutionary computing is an important research direction in the field of artificial intelligence, and its algorithm, evolutionary algorithm, is a population-based search algorithm. Because of the excellent performance of evolutionary algorithm, it has been applied in diverse fields, such as path planning [1], shop scheduling [2], multi-agent system [3], networks planning [4], bi-level optimization [5], and symbolic regression [6].

Multiobjective multitasking optimization (MTO) [7] is a new research topic in the field of evolutionary computing, which can solve multiple different multiobjective optimization problems (MOPs) simultaneously and improve the quality of the solutions through knowledge transfer. As pioneers, Gupta et al. [8] first proposed a multiobjective evolutionary multitasking (EMT) algorithm named MO-MFEA to tackle MOPs, which can improve the performance of each task through useful knowledge transfer. Thereafter, many multiobjective EMT algorithms have been proposed. According to the way of knowledge transfer, these algorithms can be divided into the following three categories: (1) adaptive knowledge transfer strategy [9,10,11,12]; (2) search space mapping strategy [13,14,15,16,17]; (3) valuable knowledge selection strategy [18,19,20].

The adaptive knowledge transfer strategy is to adaptively control the intensity of knowledge transfer according to the search process. For adaptive knowledge transfer, Bali et al. [9] changed the intensity of knowledge transfer by learning the similarity between tasks, so as to improve the performance of the algorithm. Yang et al. [10] proposed an algorithm to divide decision variables into diversity variables and convergence variables. By increasing the transfer intensity of the diversity variables, the solution distribution on Pareto front (PF) is uniform, and reducing the knowledge transfer on the convergence variables makes the population converge to PF. Zheng et al. [11] defined a capability vector to control the intensity of knowledge transfer for improving the performance of the algorithm. Zhou et al. [12] proposed the MFEA-AKT in which the crossover operators of knowledge transfer are controlled through the evolutionary state.

The search space mapping strategy is to use the learned mapping method to align the distribution in the subspace for reducing the differences between the subpopulations of different tasks. Bali et al. [13] used the linear domain adaptive method to map two tasks to a higher order representation space which is easier to share similarity, to achieve more efficient knowledge transfer. To solve the vehicle routing problem, Feng et al. [14] improved search space mapping and explicit knowledge transfer using automatic encoder to solve the problem of transfer mapping. Ding et al. [15] implemented an EMT algorithm to solve expensive optimization problems, which can promote knowledge transfer between optimization problems with different optimal locations and different number of decision variables. Liang et al. [16] introduced an algorithm called MOMFEA-SADE which builds the transfer matrix based on the subspace alignment strategy. Zhou et al. [17] proposed an algorithm named KAES which designs a kernelized autoencoding to capture nonlinearity between problems in pursuit of efficient knowledge transfer across domains.

The valuable knowledge selection strategy can find the valuable solutions to improve the efficiency of positive transfer. Feng et al. [18] proposed an algorithm named EMEA which adopts the nondominated solutions in each task as valuable knowledge to transfer, whereas this algorithm was only applicable to solve highly related tasks. Lin et al. [19] selected the new transferred solutions near the positive transferred solutions, and this method can improve the efficiency of positive knowledge transfer. In addition, Lin et al. [20] introduced an EMT algorithm according to incremental learning. In this paper, the Naive Bayes classifier finds the valuable areas through the positive transferred solutions, and selects the new transferred solutions in these areas.

The efficient knowledge transfer strategy can significantly improve the convergence speed and the quality of the solutions. Different from the previous work, this paper designs a new transfer strategy, i.e., the transfer strategy based on multidirectional prediction method. First, according to the method of binary clustering, multiple representative points are generated for the population, and the population is divided into multiple classes. Second, the prediction direction of each class is generated based on the representative points. Then the adaptive mutation strength is designed for each class according to the degree of population improvement. Finally, the predictive transferred solutions are generated by prediction directions and mutation strengths. Based on the above facts, this paper proposes a multiobjective EMT algorithm with multidirectional prediction method (EMT-MPM). The main contributions are listed as follows:

• 1. This paper is the first attempt to design an efficient transfer strategy by multidirectional prediction method.

• 2. An effective prediction direction generation method is developed to generate multiple prediction directions.

• 3. A mutation strength adaptation method is proposed to flexibly control the range of transfer.

• 4. The performance of EMT-MPM is investigated on two MTO test suits. Compared with the state-of-the-art EMT algorithms, the experimental results indicate that EMT-MPM is effective and competitive.

The rest of this paper is arranged as follows. The next section gives the related work and research motivation. The subsequent section presents the details of EMT-MPM followed by which the experimental results are presented. The final section concludes this paper and proposes several future works.

Related work

MTO problem

MTO [7] has attracted more and more attention in EMT community. MTOs aim to solve multiple different MOPs simultaneously for better solutions through knowledge transfer between tasks. Generally, an MTO problem with K tasks can be defined as follows:

$$\begin{aligned} \begin{array}{l} {\mathrm{Minimize:}}\left\{ \begin{array}{l} {F_1}({{\varvec{x}}_1}) = (f_1^1({{\varvec{x}}_1}), \cdots , f_1^{{m_1}}({{\varvec{x}}_1}))\\ {F_2}({{\varvec{x}}_2}) = (f_2^1({{\varvec{x}}_2}), \cdots , f_2^{{m_2}}({{\varvec{x}}_2}))\\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} \vdots \\ {F_j}({{\varvec{x}}_j}) = (f_j^1({{\varvec{x}}_j}), \cdots , f_j^{{m_j}}({{\varvec{x}}_j}))\\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} \vdots \\ {F_K}({{\varvec{x}}_K}) = (f_K^1({{\varvec{x}}_K}), \cdots , f_K^{{m_K}}({{\varvec{x}}_K})) \end{array} \right. \\ \\ {} {} {} {} {} {\mathrm{subject}}{} {} {} {} {\mathrm{to}}{} {} {} {} {} {{{{\varvec{x}}}}_j} \in {\Omega ^{{d_j}}},{} {} {} {} {} {} {} j = 1, 2, \cdots , K, \end{array} \end{aligned}$$

(1)

where ${F_j}$ denotes the jth multiobjective task which consists of $m_j$ objective functions; ${\varvec{x}}_j$ represents the solution in the jth task; ${\Omega ^{{d_j}}}$ denotes the search space of jth task whose dimension is $d_j$.

Prediction-based methods

Many prediction-based methods have been proposed to solve dynamic multiobjective optimization problems, which can be classified into three categories, namely, individual-based prediction [21], population-based prediction [22,23,24,25], and multidirectional prediction [26].

• 1. Individual-based prediction (INBP): The movement trajectory of each individual in the population is predicted.

• 2. Population-based prediction (POBP): One single prediction model is established for the trajectory of the entire population.

• 3. Multidirectional prediction (MULP): The population is divided into several subpopulations by clustering method, and several prediction models are established for the subpopulations.

In INBP, Zhou et al. [21] proposed an individual-based prediction method, which used individual historical information to predict the possible positions of each individual. By contrast, a population-based prediction method, named POBP, was proposed in [22], where only one single prediction model was employed for predicting the whole population. Inspired by the work in [22], some population-based prediction methods have been proposed. For example, Jiang et al. [23] presented a steady-state and generational evolutionary algorithm, which predicted the evolution direction by the center points of two adjacent moments. Peng et al. [24] introduced a method based on central point prediction combined with memory strategy for dynamic multiobjective optimization. Wu et al. [25] implemented a directed search strategy based on the center points of Pareto set. This strategy used the center point and linear time series model to predict the population movement direction and its vertical direction, and then obtained the predicted new position. In MULP, Rong et al. [26] proposed a dynamic multiobjective evolutionary algorithms based on multidirectional prediction method, which established several prediction models for the subpopulations.

Motivation

Although many transfer strategies such as adaptive knowledge transfer strategy [9,10,11,12], search space mapping strategy [13,14,15,16,17], and valuable knowledge selection strategy [18,19,20] have been applied to MTO, there is no literature that attempts to transfer solutions to promising regions through the prediction method. The core of MTO is to improve the convergence speed and the quality of the solutions through the transferred solutions between tasks. In other words, the transferred solutions are used to guide the evolution of the current task. Therefore, transferring the solutions to promising regions can improve the convergence speed and the quality of the solutions.

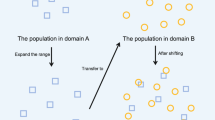
As an illustrative example, Fig. 1 shows the results of transferred solutions with both the general transfer strategy and the prediction-based transfer strategy. In Fig. 1, the pink rectangle represents the true PF of the task, the blue circle represents the current population, the green triangle represents the transferred solutions obtained by the general transfer strategy, and the red pentacle represents the transferred solutions obtained by the prediction-based transfer strategy. It can be observed that the transferred solutions obtained by the prediction-based transfer strategy are closer to the true PF, which indicates that the prediction method can transfer the solutions to more promising regions. Therefore, it is a very significant research problem to transfer the solutions to the promising region using the prediction method. In this paper, we are the first attempt to design an efficient knowledge transfer strategy based on multidirectional prediction method.

Fig. 1

The transferred solutions obtained by transfer strategy and prediction-based transfer strategy on CILS-task2

Proposed algorithm

This section presents the transfer strategy based on multidirectional prediction method. Moreover, the main framework of EMT-MPM is given. Finally, the complexity of EMT-MPM is analyzed.

Transfer strategy based on multidirectional prediction method

The transfer strategy based on multidirectional prediction method is proposed. First, the adaptive clustering method is used to divide the population into M classes. The distribution mean of each class is used as the representative point, where the number of representative points is M. Second, according to two successive generations of representative points, the evolutionary direction of each class is generated by constructing a natural gradient. Thirdly, the mutation strength of each class is calculated based on the relative improvement of two successive generations. Finally, the transferred solutions are divided into the nearest class, and the predictive transferred solutions are generated by the prediction directions and mutation strengths.

Generation representative points

The binary clustering method [26] and weighted sum method are introduced to generate representative points. First, according to binary clustering method, the center point of the population and all m extreme solutions¹ of the PF are selected and stored in the class center set $\varvec{C}$. The center point of the g generation population ${\varvec{P}_g}$ is calculated as follows:

$$\begin{aligned} {{\bar{{\varvec{x}}}}^g} = \frac{1}{N}\sum \limits _{i = 1}^N {{{\varvec{x}}}_i^g}, \end{aligned}$$

(2)

where N is the population size; ${{\varvec{x}}_i^g}$ is the ith solution of the g generation population. The mth extreme solution ${\varvec{p}_m}$ is

$$\begin{aligned} {\varvec{p}_m} = \arg \mathop {\min }\limits _{{\varvec{x}}_i^g \in {} {} {\varvec{P}_g}} {f_m}({\varvec{x}}_i^g), \end{aligned}$$

(3)

where ${f_m}$ is the mth objective function of the task; ${\varvec{P}_g}$ is the g generation population. Second, the center point of the population and m extreme solutions are used as the initial class centers, and the Euclidean distances between the solutions of the population and $m+1$ class centers are calculated. If $M > m + 1$, the farthest point in each class from the class center is the candidate class center, and this distance is defined as the class radius. Moreover, the class with the largest radius is selected, and the candidate class center of this class is used as the new center point. The process is repeated until the population is divided into M classes. Finally, the distribution mean of each class is used as the representative point by the weighted sum method and is calculated as follows:

$$\begin{aligned} {\bar{{\varvec{x}}}}_i^g = \sum \limits _{j = 1}^{N_i^g} {{w_j^g}} {\varvec{x}}_j^g, \end{aligned}$$

(4)

where $N_i^g$ is the number of the solutions in generation g of i-th class; ${\varvec{x}}_j^g$ is the j-th solution in ith class; ${w_j^g}$ is a weight and can be defined as follows:

$$\begin{aligned} {w_j^g} = \frac{{\ln ({N_i^g} + \frac{1}{2}) - \ln {R_j^g}}}{{\sum \nolimits _{k = 1}^{{N_i^g}} {(\ln ({N_i^g} + \frac{1}{2}) - \ln {R_k^g})} }},{} {} {} {} 1 \le j \le {N_i^g}, \end{aligned}$$

(5)

where $R_j^g$ is the ranking of solution ${\varvec{x}}_j^g$ in ith class, and the calculation method is

$$\begin{aligned} {R_j^g} = N_i^g - j + 1, \end{aligned}$$

(6)

where j is the number of layers for solution ${\varvec{x}}_j^g$ in the nondominated sorting of the ith class. For instance, for a nondominated solution ${\varvec{x}}_j^g$, j is equal to 1. According to Eq. (5), a better solution can get more weight, and the method of weight calculation emphasizes the top ranked solutions. In addition, it is clear that there is $\sum \nolimits _{j = 1}^{{N_i^g}} {{w_j^g}} = 1$. Specifically, the corresponding algorithm flow is shown in Algorithm 1.

Fig. 2

Schematic diagram of class centers selection process

Figure 2 depicts the process of selecting four class centers from fifteen solutions. First, the center point of the population and two extreme solutions are obtained by Eqs. 2 and 3, respectively. Second, the other solutions in the population are assigned to three classes, Class 1, Class 2, and Class 3 according to the Euclidean distance from the class center points A, B, and ${{\bar{{\varvec{x}}}}^g}$. Because points C, D, and E are the solutions farthest from the class center among the three classes, respectively, and the distance from C to the class center A is farther than that from D to ${{\bar{\varvec{x}}}^g}$ and E to B. Therefore, C is chosen as the new class center point. Thirdly, the solutions in Class 1 are divided into two classes based on the distance from A and C. Finally, four class centers are selected, and the population is divided into four classes.

Generation prediction directions

A multidirectional prediction method is proposed to predict the corresponding evolutionary direction of each class. Suppose ${\bar{{\varvec{X}}}}^{g - 1} = \{ {\bar{\varvec{x}}}_1^{g - 1}, {\bar{\varvec{x}}}_2^{g - 1}, \cdots , {\bar{\varvec{x}}}_M^{g - 1}\}$ and ${\bar{\varvec{X}}}^g = \{ {\bar{\varvec{x}}}_1^g, {\bar{\varvec{x}}}_2^g, \cdots , {{\bar{x}}}_M^g\}$ are class representative points of generation $g-1$ and generation g, respectively. First, for any representative point ${\bar{\varvec{x}}}_i^g$ in ${{\bar{\varvec{X}}}^{g}}$, the nearest representative point ${\bar{\varvec{x}}}_i^{g-1}$ in ${{\bar{\varvec{X}}}^{g-1}}$ is selected as the parent of ${\bar{\varvec{x}}}_i^g$. Second, the natural gradient²$\Delta {} {{\varvec{x}}}_i^g$ in ith class is constructed and is expressed as

$$\begin{aligned} \Delta {} {{\varvec{x}}}_i^g ={} {} {\bar{{\varvec{x}}}}_i^{g} - {} {} {} {\bar{{\varvec{x}}}}_i^{g-1}, \end{aligned}$$

(7)

where ${{\bar{\varvec{x}}}_i^{g-1}}$ and ${{\bar{\varvec{x}}}_i^{g}}$ are the representative points of generation $g-1$ and generation g in i-th class. Finally, the prediction direction ${{\hat{\Delta }}} {} {} {{\varvec{x}}}_i^g$ is defined as follows:

$$\begin{aligned} {{\hat{\Delta }}} {} {} {{\varvec{x}}}_i^g = (1 - {c_p}) {\hat{\Delta }} {} {} {{\varvec{x}}}_i^{g-1} + {c_p}\Delta {} {} {{\varvec{x}}}_i^{g} \end{aligned}$$

(8)

where $c_p$ is a parameter that controls the weight of the historical prediction direction; ${{\hat{\Delta }}} {} {} {{\varvec{x}}}_i^{g-1}$ is the prediction direction of generation ${g - 1}$ in ith class; $\Delta {} {} {{\varvec{x}}}_i^{g}$ is the natural gradient of generation g in ith class. Clearly, ${{\hat{\Delta }}} {} {} {{\varvec{x}}}_i^{g}$ is a weighted combination of the historical prediction direction ${{\hat{\Delta }}} {} {} {{\varvec{x}}}_i^{g-1}$ and the current natural gradient $\Delta {} {} {{\varvec{x}}}_i^{g}$. Thus, ${{\hat{\Delta }}} {} {} {{\varvec{x}}}_i^{g}$ is a weighted combination of all the historical natural gradients and is similar to the evolution path in [29]. According to Eqs. (7) and (8), the calculation of the prediction direction for each representative point is independent of each other, and its value can be determined by the corresponding representative point and its historical representative point. Moreover, these prediction directions are complementary to each other. By predicting the evolutionary direction of each representative point, multiple prediction directions can work together to more accurately predict the promising directions.

Fig. 3

Example for multidirectional prediction method

Figure 3 is an example to explain multidirectional prediction method. First, the population is divided into seven classes by the adaptive clustering method, and seven representative points are generated. Second, the evolutionary direction are generated according to current and historical representation points. Finally, the promising directions are predicted by seven evolutionary directions.

Calculation mutation strengths

The mutation strength is calculated to control the step size of transferred solutions. First, the concept of hypervolume (HV) [30] is introduced to compare the solution of multiobjective optimization. As shown in Fig. 4, this is an example to illustrate the concept of HV. The red dot represents the reference point. The green, blue, and yellow matrices represent the HV of points A, B, and C, respectively. Specifically, the larger HV indicates the better quality of the solution. Second, the relative improvement $\Delta _\mathrm{improv}^{i,g}$ of generation g in i-th class is defined as follows:

$$\begin{aligned} \Delta _\mathrm{improv}^{i,g} = \frac{{\sum \nolimits _{i = 1}^{N_i^g} {HV({{\varvec{x}}}_i^g)} - \sum \nolimits _{i = 1}^{N_i^{g - 1}} {HV({{\varvec{x}}}_i^{g - 1})} }}{{\sum \nolimits _{i = 1}^{N_i^{g - 1}} {HV({{\varvec{x}}}_i^{g - 1})} }}, \end{aligned}$$

(9)

where ${N_i^g}$ and ${N_i^{g - 1}}$ represent the number of the solutions in generation g and generation $g-1$ of i-th class, respectively; ${HV({{\varvec{x}}}_i^{g})}$ and ${HV({{\varvec{x}}}_i^{g - 1})}$ denote the HV of solutions ${{\varvec{x}}}_i^g$ and ${{\varvec{x}}}_i^{g-1}$ in the objective space, respectively. Finally, the mutation strength $\sigma _i^{g}$ is calculated

$$\begin{aligned} \sigma _i^{g} = \sigma _i^{g-1} \exp \left[ \frac{1}{{{d_\sigma }}}(\frac{{\Delta _\mathrm{improv}^{i,g}}}{{\Delta _\mathrm{improv}^{i,g - 1}}} - 1)\right] , \end{aligned}$$

(10)

where ${d_\sigma }$ is a damping factor, and ${d_\sigma } \ge 1$; $\Delta _\mathrm{improv}^{i,g}$ and $\Delta _\mathrm{improv}^{i,{g-1}}$ are the relative improvements of generation g and generation $g-1$ in i-th class; for initial mutation strength, $\sigma _i^0 = 1$. If the relative improvement in i-th class is greater, the greater mutation strength can be obtained. Moreover, the mutation strength of each class is independent of each other and can be adaptively controlled.

Fig. 4

Example for understanding the hypervolume

Selection strategy of transferred solutions

Since the valuable knowledge selection strategy [19] has an excellent performance in multiobjective EMT algorithms, the transferred strategy uses it to generate transferred solutions. Specifically, transferred solutions are randomly selected from each task in the first generation. When the generation $g > 1$, transferred solutions are selected according to the solutions which achieved the positive transfer in generation $g - 1$. A transferred solution achieves positive transfer if it is nondominated in its target task. Afterwards, in the original task of this positive transferred solution, its several closest solutions will be the transferred solutions since these solutions are more likely to achieve positive transfer. Therefore, the transferred solutions are selected near the positive transferred solutions, and these solutions are more valuable.

The details of the selection strategy of transferred solutions are given in Algorithm 2. The transferred solutions are selected according to the solutions which achieved the positive transfer in generation $g > 1$. If there is no positive transferred solution in $g - 1$ generation, the nondominated solutions (line 2) are selected as the transferred solutions in g generation. Otherwise, the transferred solutions (line 4) are selected near the positive transferred solutions in g generation.

Generation predictive transferred solutions

The predictive transferred solutions in each class are generated based on the prediction directions and mutation strengths. Meanwhile, to improve the performance, a Gaussian perturbation related to the mutation strength is introduced. To be specific, the predictive transferred solution ${\hat{\varvec{t}}}_j^{g}$ in ith class is calculated as follows:

$$\begin{aligned} \hat{\varvec{t}}_j^{g} = {\varvec{t}}_j^{g} + \sigma _i^{g}{{\hat{\Delta }}} {} {} {{\varvec{x}}}_i^{g}+{{\varvec{\gamma }} ^g}, \end{aligned}$$

(11)

where ${\varvec{t}}_j^{g}$ is the i-th transferred solutions in the g generation; $\sigma _i^{g}$ and ${{\hat{\Delta }}} {} {} {{\varvec{x}}}_i^{g}$ are the prediction direction and mutation strength in the g generation of i-th class, respectively; ${\varvec{\gamma }^g}$ is a Gaussian perturbation, and ${\varvec{\gamma }^g} \sim {{\mathcal {N}}}(\varvec{0},{\varvec{\sigma } ^{g}})$. The calculation method of ${\varvec{\sigma } ^{g}}$ is

$$\begin{aligned} {\varvec{\sigma }^{g}} = \frac{1}{M}\sum \limits _{i = 1}^M {\left| {{\hat{\Delta }} {} {} {\varvec{x}}_i^{g}} \right| }, \end{aligned}$$

(12)

where M is the number of classes; ${{\hat{\Delta }}} {} {} {{\varvec{x}}}_i^{g}$ is the mutation strength in the g generation of i-th class.

Algorithm 3 presents the framework of transfer strategy based on multidirectional prediction method. First, two successive generations of representative points are calculated using adaptive clustering method (lines 1–2). Second, the prediction direction and mutation strength of each class are calculated (lines 4–5). Finally, the predictive transferred solutions are obtained by combining the prediction directions with mutation strengths (line 9).

Basic workflow of the proposed method

The basic workflow of transfer strategy based on multidirectional prediction method is shown in Fig. 5. In this paper, multidirectional prediction method is combined with the selection strategy of transferred solutions to generate the predictive transferred solutions as useful information to transfer from one task to another task. Multidirectional prediction method can make use of the evolutionary directions of the population. The transferred solutions are valuable solutions selected by selection strategy. Therefore, the predictive transferred solutions make use of both the information of evolutionary directions and transferred solutions, and they are used as useful information. The generation process of predictive transferred solutions is as follows. First, the multidirectional prediction method uses the binary clustering method and weighted sum method to generate representative points. Then the prediction directions and mutation strengths are generated according to the representative points. Second, a selection strategy of transferred solutions is utilized to obtain the transferred solutions. Thirdly, the predictive transferred solutions are calculated by transferred solutions, prediction directions, mutation strengths, and Gaussian perturbation. Finally, the predictive transferred solutions are transferred between tasks as transfer knowledge.

Fig. 5

The workflow of transfer strategy based on multidirectional prediction method

Main framework

The main framework of EMT-MPM is summarized in Algorithm 4. First, the initial population of the K tasks is generated in the unified search space [7] for effectively transferring knowledge across tasks. The unified space is ${[0,1]^D}$, where $D = \max \{ {D_i}\}$ and ${D_i}$ is the decision space dimensionality of $T_i$. Then the initial populations of the K tasks are generated, and each solution in the K populations is evaluated by the corresponding optimization task (lines 1-2). Second, the predictive transferred solutions of the K tasks are selected through the transfer strategy based on multidirectional prediction method (line 5). Suppose $L_k$ and $U_k$ are the lower and upper boundaries of $T_k$, respectively. The formula of transferring a solution ${\hat{\varvec{t}}}_j^{g}$ from $T_i$ to $T_k$, denoted as ${\hat{\varvec{t}'}}_j^g$, is shown as follows:

$$\begin{aligned} {\hat{\varvec{t}'}}_j^g = \frac{{\hat{\varvec{t}}_j^g - {L_i}}}{{{U_i} - {L_i}}}({U_k} - {L_k}) + {L_k}, \end{aligned}$$

(13)

where $L_i$ and $U_i$ are the lower and upper boundaries of $T_i$, respectively. When ${D_k} \ne {D_i}$, this formula can be modified according to the strategy proposed in [15]. To further improve the performance of knowledge transfer, the predictive transferred solution ${\hat{\varvec{t}'}}_j^g$ is multiplied by a distributed factor $\xi$ with a probability p to obtain the new predictive transferred solution ${\hat{\varvec{t}''}}_j^g$ (lines 7–9) and is defined as follows:

$$\begin{aligned} {\hat{\varvec{t}''}}_j^g = \xi {} {} {\hat{\varvec{t}'}}_j^g, \end{aligned}$$

(14)

where $\xi$ is a distributed factor, and $\xi \sim U(0,2)$. By the distributed factor, the new predictive transferred solution can explore a large range and find the promising regions. Finally, the environmental selection is implemented on population $\varvec{P}_i^g \cup {{\hat{\varvec{T}}}''_g} \cup {\varvec{O}}_i^g$ to select N best solutions, and the new populations $\varvec{P}_i^{g + 1}$ are generated (line 14).

Complexity analysis

For the convenience of the analysis, it is assumed that the number of tasks in Algorithm 4 is set to K. The population size for each task is set to N. The number of decision variables and objectives are set to n and m, respectively. $\lambda$ is the number of transferred solutions. M is the number of representative points. From lines 1–2 in Algorithm 4, the population initialization and the evaluation of solutions in K tasks are performed, and the computational complexity of this process is $O(K{N^2}m)$. In line 5 of Algorithm 4, the predictive transferred populations of K tasks are obtained by Algorithm 3. First, M representative points in K tasks are generated, and its computational complexity is O(KNM). Second, the computational complexity of M prediction directions in K tasks is O(KNM). Thirdly, the computational complexity of the mutation strengths and the predictive transferred solutions are $O(KN{m^2})$ and $O(K\lambda )$, respectively. From lines 12-14, the algorithm mainly performs nondominated sorting and environment selection, and its computational complexity is $O(K{N^2}m)$. In summary, the worst computational complexity of the proposed algorithm is $O(K{N^2}m)$ or O(KNM) or $O(KN{m^2})$, whichever is larger.

Remarks

For the transfer strategy based on multidirectional prediction method, four comments are made.

• 1. Compared with the multidirectional prediction method in dynamic multiobjective optimization [26], the proposed multidirectional prediction method has the following four differences. First, the proposed method introduces the weighted sum method to calculate the representative points, and these representative points have better objective function values. This is because the solution with the better objective function value has greater weight. Second, when calculating the prediction directions, the proposed method makes use of representative points of two successive generations and historical prediction direction at the same time. In comparison with the multidirectional prediction method in dynamic multiobjective optimization, the proposed method can obtain the promising prediction directions. Thirdly, the multidirectional prediction method in dynamic multiobjective optimization uses a fixed mutation strength. By contrast, the proposed method can adaptively control the mutation strength according to the improvement degree of each class. Fourth, the predictive transferred solutions generated by the proposed method are to help the target task as transfer knowledge. However, the prediction solutions generated by the multidirectional prediction method in dynamic multiobjective optimization are used as a new initial population.

• 2. The binary clustering method is used to generate M class centers. Compared with the traditional K-means clustering method, the binary clustering method only needs to reclassify a corresponding class after getting the new class center, but does not need to classify all the individuals. This greatly reduces the computational complexity in the process of generating the class center point. Moreover, when generating the prediction direction, the weight of the current and historical directions can be flexibly controlled by the parameter $c_p$.

• 3. HV indicator is introduced into MTO to define the improvement degree of solution. Then the algorithm adaptively controls the mutation strength by the improvement degree of each class. Moreover, different mutation strengths are set for different classes, which ensures that each class can flexibly control according to its own evolutionary state.

• 4. Each class generates the predictive transferred solutions by the prediction directions, mutation strengths, and Gaussian perturbation. Then the predictive transferred solutions generated in each class can transfer to promising regions. In addition, Gaussian perturbation mainly guarantees the validity and diversity of the predictive transferred solutions.

Experimental studies

In this section, NSGA-II [31], MO-MFEA [7], EMEA [18], MOMFEA-SADE [16], EMT/ET [19], MO-MFEA-II [9], TMO-MFEA [10], EMTIL [20], and EMT-PD [32] are used to compare with EMT-MPM on two MTO test suits. Moreover, the performance of EMT-MPM is analyzed in depth. Finally, the following points will be demonstrated.

• 1. EMT-MPM can significantly outperform NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, EMT/ET, MO-MFEA-II, TMO-MFEA, EMTIL, and EMT-PD.

• 2. The transfer strategy based on multidirectional prediction method in EMT-MPM can transfer the solutions to the promising regions and significantly improve the performance of the algorithm.

Table 1 Average value and standard deviation of IGD for NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, EMT/ET, and EMT-MPM on the first test suit

Table 2 Average value and standard deviation of IGD for MO-MFEA-II, TMO-MFEA, EMTIL, EMT-PD, and EMT-MPM on the first test suit

Test problems and performance metric

The two test suits are used to demonstrate the performance of EMT-MPM. The CEC 2017 MTO benchmarks [33] are used as the first test suit which contains nine MTO problems. The second test suit named CPLX contains ten complex benchmark problems, which is presented for WCCI 2020 Competition on Evolutionary Multitasking Optimization [34].

In this paper, the inverted generational distance (IGD) [35] is used to evaluate the performance of all comparison algorithms. IGD measures the average of the minimum distance between the solutions of the real PF and the approximate solution set obtained by the algorithm. Therefore, calculating IGD requires obtaining a set of solutions that are uniformly sampled on the real PF in advance. Let ${\varvec{P}^*}$ be a set of solution sets uniformly sampled on the real PF, and $\varvec{S}$ is the PF approximate solution set obtained by the comparison algorithms. The IGD is calculated as follows:

$$\begin{aligned} IGD(\varvec{S},{\varvec{P}^*}) = \frac{{\sum \nolimits _{{\varvec{x}} \in {\varvec{P}^*}} {dist({\varvec{x}},\varvec{S})} }}{{\left| {{\varvec{P}^*}} \right| }}, \end{aligned}$$

(15)

where ${dist({\varvec{x}}, \varvec{S})}$ is the Euclidean distance between solution ${\varvec{x}} \in {\varvec{P}^*}$ and the nearest solution on $\varvec{S}$; $\left| {{\varvec{P}^*}} \right|$ is the cardinality of the set ${\varvec{P}^*}$. The smaller the IGD value, the better the convergence and diversity of $\varvec{S}$.

Parameter settings

The parameter settings of all algorithms are listed below.

• 1. Population Size: MO-MFEA, MOMFEA-SADE, MO-MFEA-II, TMO-MFEA, and EMT-PD are set to 200, and each population for EMEA, EMT/ET, EMT-MPM, and EMTIL is 100. To be fair, the population size of NSGA-II is 100.

• 2. Maximum number of function evaluations: NSGA-II is set to 50000, and all other algorithms are set to 100000.

• 3. Independent number of runs: All algorithms are set to 20.

• 4. Random mating probability (rmp): MO-MFEA, MOMFEA-SADE, and EMT-PD are set to 0.3. MO-MFEA-II is set as either 0.9, 0.6, or 0.3. TMO-MFEA is set to 1 and 0.3 for diversity variable and convergence variable, respectively.

• 5. Operator of generating offspring: For NSGA-II, MO-MFEA, EMEA, EMT/ET, MO-MFEA-II, TMO-MFEA, EMTIL, EMT-PD, and EMT-MPM, simulated binary crossover (SBX) [36] and polynomial mutation (PM) [37] are adopted. The parameter settings of SBX and PM for the seven algorithms are ${p_c} = 0.9$, ${p_m} = 1/{D_\mathrm{max}}$, ${\eta _c} = 20$, and ${\eta _m} = 15$, where $D_\mathrm{max}$ is the largest dimension of all tasks. For MOMFEA-SADE, DE operators are used. The crossover rate CR is set to 0.6, and the scale factor F takes 0.5.

• 6. Number ($\lambda$) of transferred solutions: For EMEA, EMT/ET, EMTIL, and EMT-MPM, $\lambda$ is set to 10, 8, 10, and 8, respectively.

• 7. Other parameters: $M=6$, $c_p=0.7$, $d_\sigma =2$, and $p=0.5$, since they can obtain the best performance on the experiments.

Results and statistical analysis

Comparison of NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, EMT/ET, MO-MFEA-II, TMO-MFEA, EMTIL, EMT-PD, and EMT-MPM on the first test suit

The first test suit is utilized to verify the performance of EMT-MPM. The experimental results obtained by all algorithms over 20 runs are shown in Tables 1 and 2, respectively. The symbols “$+$”, “$\approx$”, and “−” represent that EMT-MPM is better, similar or worse than the compared algorithms, respectively. In addition, the best result of every task is marked in bold.

Table 1 gives the average value and standard deviation of IGD for NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, EMT/ET, and EMT-MPM on the first test suit. The performance of NSGA-II is significantly worse than the five multiobjective EMT algorithms, which shows the effectiveness of knowledge transfer between different tasks. Moreover, the performance of EMT-MPM is significantly superior to MO-MFEA, EMEA, MOMFEA-SADE, and EMT/ET, which benefits from the proposed multidirectional prediction method. In addition, Table 2 shows the average value and standard deviation of IGD for MO-MFEA-II, TMO-MFEA, EMTIL, EMT-PD, and EMT-MPM on the first test suit. As shown in Table 2, EMT-MPM surpasses MO-MFEA-II, TMO-MFEA, EMTIL, and EMT-PD on 18, 18, 18, and 17 tasks, respectively. This indicates that the proposed multidirectional prediction method can obtain more promising transferred solutions. Furthermore, this paper conducts Friedman’s test [38] on six compared algorithms based on the first test suit to IGD. Table 3 presents the test results that EMT-MPM has the best ranking to IGD, sequentially followed by EMT/ET, MOMFEA-SADE, EMT-PD, EMEA, EMTIL, TMO-MFEA, MO-MFEA-II, MO-MFEA, and NSGA-II.

In summary, the experimental results show that EMT-MPM has the best performance except for CILS-T1, NIHS-T1, and NILS-T1. This is because the transfer strategy based on multidirectional prediction method can transfer solutions to promising regions by prediction directions and mutation strengths. Moreover, the validity and diversity of predictive transferred solutions can be improved by Gaussian perturbation. Therefore, the predictive transferred solutions can guide the current task to accelerate evolution and improve the quality of the solutions.

Comparison of NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, EMT/ET, and EMT-MPM on the second test suit

Table 4 shows the experiment results by six compared algorithms on the second test suit. As shown in Table 4, EMT-MPM surpasses NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, and EMT/ET on 20, 20, 18, 18, and 17 tasks, respectively. As a comparison, EMT-MPM is surpassed by NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, and EMT/ET on 0, 0, 2, 2, and 3 tasks, respectively. This indicates that EMT-MPM can achieve excellent performance on the second test suit. What’s more, Friedman’s test on six compared algorithms based on the second test suit to IGD is conducted. Table 5 shows that EMT-MPM obtains the best ranking, which indicates that the multidirectional prediction method is effective for MTO problems.

Table 3 Results obtained for NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, EMT/ET, MO-MFEA-II, TMO-MFEA, EMTIL, EMT-PD, and EMT-MPM by the Friedman’s test on the first test suit to IGD

Table 4 Average value and standard deviation of IGD for NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, EMT/ET, and EMT-MPM on the second test suit

Analysis of the convergence trends of the algorithms

As shown in Fig. 6, the convergence trends of NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, EMT/ET, and EMT-MPM on three representative problems of the first test suit is illustrated. The lines in Fig. 6 represent the average IGD values of the six compared algorithms. The convergence speed of NSGA-II is the slowest in most problems, which indicates that the transferred knowledge between tasks is useful. Moreover, the convergence speed of EMT-MPM is significantly faster than the other five compared algorithms, which illustrates that the proposed transfer strategy based on multidirectional prediction method can significantly improve the performance of the algorithm. This phenomenon also shows that EMT-MPM can transfer more valuable knowledge. In conclusion, the performance of EMT-MPM is significantly better than other algorithms. Therefore, the proposed multidirectional prediction method is an efficient method for MTO.

Effectiveness of the proposed method

The proposed transfer strategy based on multidirectional prediction method mainly includes prediction direction, mutation strength, and Gaussian perturbation. First, to verify the effectiveness of the prediction direction, only the natural gradient is used as the prediction direction. This algorithm is constructed, namely EMT-NG. Second, the mutation strength is set as 1 to verify its effectiveness, and the corresponding algorithm is defined as EMT-NMS. Thirdly, the Gaussian perturbation in the EMT-MPM algorithm is removed, which is defined as EMT-NGP. Finally, EMT-NG, EMT-NMS, EMT-NGP, and EMT-MPM are run 20 times on the first test suit.

Table 5 Results obtained for NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, EMT/ET, and EMT-MPM by the Friedman’s test on the second test suit to IGD

Fig. 6

The convergence trends of NSGA-II, MO-MFEA, EMEA, MOMFEA-SADE, EMT/ET, and EMT-MPM over 20 times on three representative problems of the first test suit

Table 6 Average value and standard deviation of IGD for EMT-NG, EMT-NMS, EMT-NGP, and EMT-MPM on the first test suit

Table 7 Average value and standard deviation of IGD for $M =4$, $M = 5$, $M = 6$, $M =7$, and $M =8$ on the first test suit

Table 6 gives the average value and standard deviation of IGD values obtain by four multiobjective EMT algorithms. EMT-MPM surpasses EMT-NG, EMT-NMS, and EMT-NGP on 18, 16, and 16 tasks, respectively. In contrast, EMT-MPM is surpassed by EMT-NG, EMT-NMS, and EMT-NGP on 0, 2, and 2 tasks, respectively. Therefore, the experimental results indicate that each part of the proposed multidirectional prediction method is effective.

Parameter sensitivity analysis

In EMT-MPM, M controls the number of representative points. To analyze the effect of M, the experiments are conducted on the first test suit. M is set as 4, 5, 6, 7, and 8, respectively. Table 7 shows the experimental results by EMT-MPM with different M. When $M = 6$, EMT-MPM has the best performance. In addition, EMT-MPM has the worst performance when $M = 4$. This is because too few representative points lead to too few promising directions. When $M > 6$, the performance of EMT-MPM decreases gradually. When the number of representative points is too large, there will be too few points in each class, resulting in inaccurate prediction directions.

Conclusion

In this paper, a multiobjective EMT algorithm based on multidirectional prediction method is presented. First, the binary clustering method is used to generate multiple classes and corresponding representative points. Second, two successive generations of representative points are used to generate the prediction direction for each class. Then the mutation strength is adaptively controlled according to the improvement degree of each class. Thirdly, each class generates the predictive transferred solutions by the prediction directions and mutation strengths. Finally, EMT-MPM is compared with one multiobjective algorithm and four multiobjective EMT algorithms on two MTO test suits. Experimental results demonstrate that EMT-MPM achieves excellent performance.

For future work, some new prediction methods such as support vector regression predictor and adaptive multilevel prediction can be introduced to MTO. Then it is also an interesting idea to combine prediction method with subspace alignment technique. Moreover, it is very meaningful to extend the proposed EMT-MPM algorithm to the practical application.