Introduction

The multi-objective optimization problem (MOP) [1,2,3] can be written as:

$$\begin{aligned}&\mathrm{minimize} \quad {\mathbf {f}}({\mathbf {x}}) = (f_1({\mathbf {x}}),\ldots ,f_m({\mathbf {x}}))^\intercal ,\nonumber \\&\text {s.t.} \quad {\mathbf {x}}\in \Omega , \end{aligned}$$
(1)

where \(\Omega \subset R^n\) is an n-dimensional closed subset called the decision space, \({\mathbf {x}} = (x_1,\ldots ,x_n)^\intercal \) is a decision vector, and \({\mathbf {f}}({\mathbf {x}}) = (f_1({\mathbf {x}}),\ldots ,f_m({\mathbf {x}}))^\intercal \) is the corresponding objective vector.

Given two solutions \({\mathbf {x}}^1\) and \({\mathbf {x}}^2\), \({\mathbf {x}}^1\) is said to Pareto-dominate \({\mathbf {x}}^2\) if \(\forall i \in {1,\ldots ,m}: f_i({\mathbf {x}}^1) \le f_i({\mathbf {x}}^2)\) and \(\exists i\in {1,\ldots ,m}:f_i({\mathbf {x}}^1) < f_i({\mathbf {x}}^2)\). A solution \({\mathbf {x}}^{*}\) is said to be Pareto optimal, if there is no solution that Pareto dominates it. The set of all Pareto optimal solutions is called the Pareto set (PS). The mapping of the PS in the objective space is called the Pareto front (PF). Multi-objective evolutionary algorithms (MOEAs) aim at yielding a set of uniformly distributed solutions to approximate the PF.

Fig. 1
figure 1

Illustrations of a DRS from three different views

Full size image

Many MOEAs (e.g., NSGA-II [4], SPEA2 [5] and PAES [6]) have been developed based on the Pareto-dominance criterion. However, recent studies reveal that these Pareto-dominance-based MOEAs may be hindered by dominance resistant solutions (DRSs) [7,8,9,10]. DRSs are located on some boundaries of the objective space, which can hardly be dominated by other solutions but is far away from the PF. As shown in Fig. 1, point B is a DRS located on the boundary parallel to the \(f_3\) axis. It can see that B is significantly inferior to the solutions on the PF. But it can only be dominated by the solutions on the line AB (red line in Fig. 1). Note that the probability of finding these solutions with evolutionary algorithms is very small. As a result, DRSs are always treated as non-dominated solutions and survive in the population. If the size of these boundaries is much larger than that of the PF (as in Fig. 1 where the area of each rectangular boundary region is much larger than that of the triangular PF), the most obtained solutions will be DRSs. In other words, Pareto-dominance-based MOEAs will be misled to approximate those boundaries instead of approximating the PF.

Since DRSs are often encountered in multi-objective optimization, it is imperative to enable MOEAs to eliminate DRSs from the current population [7]. Very recently, several algorithms have been demonstrated to be effective in eliminating DRSs. As a relaxed form of the Pareto-dominance criterion, the \(\epsilon \)-dominance criterion [11] is considered to be one of the most useful coping strategies. The \(\epsilon \)-dominance-based MOEAs allow each solution to have a larger dominating region, thereby a DRS has a larger probability of being dominated by a solution on the PF. Besides, a modified NSGA-II (denoted as mNSGA-II) has also demonstrated the ability to eliminate DRSs [12]. In addition, [7, 12] have indicated that some decomposition-based MOEAs (e.g., MOEA/D-PBI [13] and MOEA/D-Gen [14]) are capable of getting rid of DRSs.

This paper argues that these MOEAs capable of eliminating DRSs may in turn suffer from missing some boundary solutions of the PF. These algorithms can hardly distinguish boundary solutions of an extremely convex PF (ECPF) from DRSs. To demonstrate it, we propose a new multi-objective optimization test problem with the ECPF and DRSs. Using this test problem with 3, 5, 8, and 10 variables, we investigate the performance of six representative MOEAs in terms of boundary solutions preservation and DRS elimination. Our experimental results indicate that there is a dilemma between eliminating DRSs and preserving boundary solutions of the ECPF.

The remainder of this paper is organized as follows: “MOEAs for DRS elimination” introduce some MOEAs capable of eliminating DRSs. In “Dilemma between DRS elimination and boundary solutions preservation”, an example is given to illustrate the dilemma between boundary solutions preservation and DRS elimination. In “Scalable MOP with the ECPF and DRSs”, we propose a scalable test problem. “Experimental study” presents experimental results of six representative MOEAs on the proposed test problem. Finally, we conclude this paper in “Conclusion”.

MOEAs for DRS elimination

This section introduces and verifies the DRS eliminating capabilities of five MOEAs from three different categories, namely \(\epsilon \)-MOEA [11] and mNSGA-II [12] (dominance-based MOEAs), MOEA/D-PBI [13] and MOEA/D-Gen [14] (decomposition-based MOEAs) and SMS-EMOA [15] (indicator-based MOEA).

\(\epsilon \)-MOEA: The \(\epsilon \)-dominance criterion is used in \(\epsilon \)-MOEA and it can be written as follows. Let \(\mathbf {\epsilon } = (\epsilon _1,\ldots ,\epsilon _m)^\intercal \) and (\(\epsilon _i > 0\)) for \(i=1,\ldots ,m\), a solution \({\mathbf {x}}^1\) is said to \(\epsilon \)-dominate another solution \({\mathbf {x}}^2\), if \(f_i({\mathbf {x}}^1)-\epsilon _i \le f_i({\mathbf {x}}^2)\) for all \(i = 1,\ldots ,m\), and \(f_j({\mathbf {x}}^1)-\epsilon _j < f_j({\mathbf {x}}^2)\) for at least one \(j \in \{1,\ldots ,m\}\). The \(\epsilon \)-dominance criterion lets each solution have a larger dominating area, thereby increasing the probability of DRSs being dominated by Pareto optimal solutions.

mNSGA-II: As reported in [16], the modification of the objective values of each solution can decrease the negative effect of DRSs. The modified objective value is defined as:

$$\begin{aligned} u_i({\mathbf {x}})=(1-\alpha )f_i({\mathbf {x}})+\frac{\alpha }{m}\sum _{j=1}^{m}f_j({\mathbf {x}}), \quad i=1,\ldots ,m, \end{aligned}$$
(2)

where \(\alpha \) is a non-negative real number (\(0 \le \alpha \le 1\)). A property of DRS is that it is near-optimal on some objectives but very poor on other objectives. When evaluating one objective value for a solution, mNSGA-II also takes the other objectives values into account. Therefore, the fitness values of DRSs are decreased significantly. However, the performance of mNSGA-II is greatly affected by the value of \(\alpha \).

MOEA/D-PBI and MOEA/D-Gen: The decomposition-based MOEA converts an MOP into a set of single-objective sub-problems and optimizes them simultaneously. Different aggregation functions are adopted in MOEA/D-PBI and MOEA/D-Gen. The sub-problem in MOEA/D-PBI is defined as:

$$\begin{aligned} \text {minimize}\ g^{\mathrm{pbi}}({\mathbf {x}}\vert {\mathbf {w}},{\mathbf {z}}^*) = d_1 + \theta d_2, \end{aligned}$$
(3)

where \(d_1 =\frac{\left| ({\mathbf {f}}({\mathbf {x}})-{\mathbf {z}}^*)^\intercal {\mathbf {w}}\right| }{\Vert {\mathbf {w}}\Vert _2}\) and \(d_2 = \Vert {\mathbf {f}}({\mathbf {x}})-({\mathbf {z}}^*+d_1\frac{{\mathbf {w}}}{\Vert {\mathbf {w}}\Vert _2})\Vert _2\); \({\mathbf {w}}=(w_{1},\ldots ,w_{m})^{\intercal }\) is a weight vector that satisfies \(w_{i}\ge 0\) for all \(i=1,\ldots ,m\) and \(\sum _{i=1}^{m}w_{i}=1\); \({\mathbf {z}}^{*} = (z^{*}_1,\ldots ,z^{*}_m)^\intercal \) is the ideal point, i.e., \(z^{*}_i = \mathop {\min }\{{f_{i}}({\mathbf {x}})|{\mathbf {x}}\in \Omega \}\); \(\theta \) is a positive parameter. The subproblem in MOEA/D-Gen is defined as:

(4)

where \(\delta \) and \(\rho \) are two small positive parameters; \({\mathbf {w}}\) is a weight vector; \({\mathbf {z}}^{*}\) is the ideal point. The sub-problem’s contour line in MOEA/D-PBI and MOEA/D-Gen can be flexibly changed by adjusting their corresponding parameters [17]. Thus, both MOEA/D-PBI and MOEA/D-Gen can decrease the negative effect of DRSs.

SMS-EMOA: SMS-EMOA is one of the most popular indicator-based MOEAs. It compares each solution’s hypervolume contribution in environmental selection. The DRS is located on the boundary of the objective space and often has a very small hypervolume contribution. Therefore, the solutions on the PF rather than DRSs tend to be preserved in SMS-EMOA. However, the calculation of SMS-EMOA is very time-consuming, especially for many-objective problems.

Experimental settings and performance metrics

To illustrate the DRS eliminating capabilities of the five MOEAs, we compare their performance with NSGA-II on the three-objective mDTLZ1-4 [7]. The three-objective mDTLZ problem’s objective space has three hardly dominated boundaries (HDBs) where DRSs are located on. The number of decision variables of each mDTLZ problem is set to 10.

The population size of each algorithm is set to 190. Each algorithm is terminated after 100,000 function evaluations and conducted 30 independent runs. The simulated binary crossover [18] and the polynomial mutation operators are adopted for new solution generation. According to the relevant references [7, 12, 13], \(\theta \) in MOEA/D-PBI is set to 5, \(\rho \) in MOEA/D-Gen is set to 0.01, \(\epsilon \) in \(\epsilon \)-MOEA is set to 0.06, and \(\alpha \) in mNSGA-II is set to 0.1. The reference point in SMS-EMOA is set to \({\mathbf {f}}^{\mathrm{max}} + \sigma \), where \({\mathbf {f}}^{\mathrm{max}}=(f_1^{\mathrm{max}},\ldots ,f_m^{\mathrm{max}})\), and \(f_i^{\mathrm{max}}\) for \(i\in \{1,\ldots ,m\}\) is the maximum value of the current population in terms of the i-th objective.

In this paper, the IGD [19, 20] and HV [21] metrics are used to evaluate the performance of the obtained solution sets. Given that \(P^*\) is a set of uniformly distributed solutions along the PF and P is the set of obtained approximate objective vectors, the IGD metric value is calculated as:

$$\begin{aligned} \mathrm{IGD}(P^*,P) = \frac{\sum _{{\mathbf {v}}\in P^*}d({\mathbf {v}},P)}{\vert P^*\vert } , \end{aligned}$$
(5)

where \(d({\mathbf {v}},P)\) is the minimum Euclidean distance between the objective vector \({\mathbf {v}}\) and the approximate set P.

For the approximate set S in the decision space, the HV metric is defined as:

$$\begin{aligned} \mathrm{HV}(S) = \mathrm{VOL}\Big (\mathop {\cup }\limits _{{\mathbf {x}}\in S}[f_1({\mathbf {x}}),z_1^*]\times \cdots \times [f_m({\mathbf {x}}),z_m^*]\Big ), \end{aligned}$$
(6)

where \({\mathbf {z}}^* = (z_1^*,\ldots ,z_m^*)^\intercal \) is a reference point, and \(\mathrm{VOL}\) is the Lebesgue measure. \({\mathbf {z}}^*\) is set to \((1.1,1.1,1.1)^\intercal \) in this section.

Table 1 IGD values of the six algorithms on three-objective mDTLZ test problems
Full size table
Table 2 HV values of the six algorithms on three-objective mDTLZ test problems
Full size table
Fig. 2
figure 2

Plots of the final solutions with the median IGD-metric values found by the six MOEAs on three-objectives mDTLZ1

Full size image

Experimental results on the three-objective mDTLZ1-4

The IGD and HV metric values obtained by the six MOEAs are shown in Tables 1 and 2. Moreover, Fig. 2 plots the objective vectors which have the median IGD metric values among each algorithm’s 30 runs on mDTLZ1. We can see from Fig. 2 that NSGA-II is misled by DRSs and fails to approximate the PF of mDTLZ1. In contrast, the objective vectors achieved by the other five algorithms are mostly on the PF. The results in Tables 1 and 2 also indicate that the five MOEAs can significantly outperform NSGA-II on mDTLZ1-4. Among the five MOEAs, SMS-EMOA yields the best performance. The objective vectors achieved by SMS-EMOA have a very good distribution. For \(\epsilon \)-MOEA and mNSGA-II, the obtained objective vectors are not as evenly distributed as those yielded by SMS-EMOA. Although the majority of the objective vectors achieved by MOEA/D-PBI and MOEA/D-Gen are located on the PF, they still keep some undesirable DRSs.

Overall, NSGA-II cannot deal with DRSs and its performance severely degraded on the four MOPs. The other five MOEAs are capable of eliminating DRSs and most of the non-dominated objective vectors they gained are around the PF.

Fig. 3
figure 3

Illustration of the boundary solutions of the ECPF

Full size image

Dilemma between DRS elimination and boundary solutions preservation

In this paper, we argue that these MOEAs with DRS eliminating strategies may in turn miss some boundary solutions of the ECPF. The preservation of the ECPF’s boundary solutions is very important in many real-world applications (e.g., the agile satellite mission planning [22] and the search-based software engineering [23]). These boundary solutions could be the best candidates when the decision-maker is biased towards one or multiple objectives. However, the MOEAs with DRS eliminating strategies may fail to obtain these boundary solutions. Figure 3 gives an example of a two-objective MOP with the ECPF. Points A, B and C are three solutions on the ECPF. B and C are two boundary solutions. The areas Pareto-dominated and \(\epsilon \)-dominated by B are shown with the black dash line and the blue dot-dash line, respectively. It can be seen that A cannot be Pareto-dominated by B, but it is \(\epsilon \)-dominated by B. It means that the boundary solutions of the ECPF can easily be \(\epsilon \)-dominated by the other Pareto-optimal solutions so that they are unlikely to be retained by \(\epsilon \)-dominance based MOEAs.

Fig. 4
figure 4

Plots of the solutions obtained by the six MOEAs on an example MOP with the ECPF

Full size image

To illustrate their poor performance in boundary solutions preservation, we propose a new two-objective test problem with the ECPF. The test problem is formulated as:

$$\begin{aligned} \text {minimize}\ \left\{ \begin{array}{ll} f_1({\mathbf {x}}) = (0.5-x_1+x_2)^4, \\ f_2({\mathbf {x}}) = (0.5+x_1-x_2)^4, \end{array} \right. \end{aligned}$$
(7)

where \(\mathbf{x }=(x_1,x_2)^\intercal \in [0,0.5]^2\). The PF of this problem is \(f_1^{\frac{1}{4}}(\mathbf{x })+f_2^{\frac{1}{4}}(\mathbf{x })=1\), where \(0\le f_i(\mathbf{x })\le 1\), \(i=1,2\). The six MOEAs (i.e., \(\epsilon \)-MOEA, mNSGA-II, MOEA/D-PBI, NSGA-II, MOEA/D-Gen and SMS-EMOA) are conducted on this problem. The parameter settings of these algorithms are kept the same as in “MOEAs for DRS elimination”.

Each algorithm is performed only once on the test problem, as very similar results appear in their multiple independent runs. Figure 4 shows the objective vectors obtained by each algorithm. It can be seen that \(\epsilon \)-MOEA, mNSGA-II, MOEA/D-PBI and MOEA/D-Gen can only yield the objective vectors around the center of the ECPF. None of the obtained objective vectors is located on the boundaries of the ECPF. SMS-EMOA can obtain the boundary solutions of the ECPF. However, the number of solutions obtained by SMS-EMOA around the two boundary solutions is tremendously different from that achieved by NSGA-II. These results reveal that the boundary solutions of the ECPF are easily missed by these MOEAs with DRS eliminating strategies. In other words, there is a dilemma between DRS elimination and boundary solutions preservation.

Scalable MOP with the ECPF and DRSs

To demonstrate the dilemma between DRS elimination and boundary solutions preservation, we propose a new scalable MOP with the ECPF and HDBs (denoted as MOP-CH). In MOP-CH, the decision vector \({\mathbf {x}} = (x_1,\ldots ,x_{n})^\intercal \in [0,1]^n\) is divided into two independent parts: \({\mathbf {x}}_{\mathbf {I}} = (x_1,\ldots ,x_{m-1})^\intercal \) and \({\mathbf {x}}_\mathbf {II} = (x_m,\ldots ,x_n)^\intercal \), where \({\mathbf {x}}_{\mathbf {I}}\) are position variables and \({\mathbf {x}}_\mathbf {II}\) are distance variables. Then the m-objective MOP-CH can be written as:

$$\begin{aligned}&{\mathrm{minimize}}\ f_k({\mathbf {x}})\nonumber \\&\quad =(1-h_k^p({\mathbf {x}}_{\mathbf {I}}))(1+g_k({\mathbf {x}}_{\mathbf {II}})), \quad {\mathrm{for}}\ k = 1,\ldots ,m,\nonumber \\ \end{aligned}$$
(8)

where p (\(0<p<1\)) is a parameter that determines the curvature of the convex PF. The smaller p is, the more convex of the PF. In this paper, p is set to 0.25.

The position functions in MOP-CH are defined as:

$$\begin{aligned} h_k({\mathbf {x}}_{\mathbf {I}}) = \left\{ \begin{array}{ll} 1-x_1,&{}\quad k=1, \\ (1-x_k)\prod _{i=1}^{k-1}x_i,&{}\quad k=2,\ldots ,m-1, \\ \prod _{i=1}^{m-1}x_i,&{}\quad k=m. \end{array} \right. \end{aligned}$$
(9)

The distance functions in MOP-CH are given as:

$$\begin{aligned} g_k({\mathbf {x}}_{\mathbf {II}}) = 100\left( \vert \phi _k \vert + \sum \limits _{i\in \phi _k}((x_i-0.5)^2)-\cos \big (20\pi (x_i-0.5))\right) ,\nonumber \\ \end{aligned}$$
(10)

where \(\phi _k = \lbrace m-1+k,2m-1+k,\ldots ,\lfloor \frac{n+1-k}{m}\rfloor m-1+k\rbrace \) for \(k = 1,\ldots ,m\).

Let \({\mathbf {y}}^*\) = (\(y_1^*,\ldots ,y_m^*\)) be a Pareto optimal solution in the objective space. Then the PF of MOP-CH can be written as:

$$\begin{aligned} \sum \limits _{i=1}^m (y_i^*-1)^4=1, \end{aligned}$$
(11)

where \(0\le y_i^*\le 1\) for \(i=1,\ldots ,m\). The PF and HDBs of the three-objective MOP-CH are shown in Fig. 5.

Fig. 5
figure 5

Illustrations of the PF and the HDBs of the three-objective MOP-CH from different views

Full size image

Experimental study

Experience Results on MOP-CH

Table 3 HV values obtained by the six MOEAs on MOP-CH
Full size table
Fig. 6
figure 6

Obtained solution set with the median HV value in the 30 runs of each algorithm on the three-objective MOP-CH

Full size image

Using MOP-CH with various numbers of objective functions, we investigate the performance of the six MOEAs in terms of boundary solutions preservation and DRS elimination. The parameter settings are the same as in “MOEAs for DRS elimination”.

Experimental results are shown in Table 3, where the best results are highlighted in bold. On the three-objective MOP-CH, it can be seen that NSGA-II performs worst since it has the lowest HV mean value among the six algorithms. The decomposition-based MOEAs (i.e., MOEA/D-PBI and MOEA/D-Gen) and the dominance-based MOEAs (i.e., \(\epsilon \)-MOEA and mNSGA-II) perform better than NSGA-II. However, none of them performs as well as SMS-EMOA. On the many-objective problems, NSGA-II is still the worst one as it cannot cope with DRSs. The decomposition-based MOEAs (i.e., MOEA/D-PBI and MOEA/D-Gen) outperform the dominance-based MOEAs (i.e., \(\epsilon \)-MOEA and mNSGA-II). MOEA/D-PBI achieves the best performance on the MOP-CH with 5, 8, 10 objective functions. SMS-EMOA is not performed on the many-objective problems. The time required for its hypervolume contribution calculation is unaffordable.

Fig. 7
figure 7

Solution sets obtained by MOEA/D-PBI with different \(\theta \) on the three-objective MOP-CH

Full size image
Fig. 8
figure 8

Solution sets obtained by MOEA/D-Gen with different \(\rho \) on the three-objective MOP-CH

Full size image
Fig. 9
figure 9

Solution sets obtained by \(\epsilon \)-MOEA with different \(\epsilon \) on the three-objective MOP-CH

Full size image
Fig. 10
figure 10

Solution sets obtained by mNSGA-II with different \(\alpha \) on the three-objective MOP-CH

Full size image
Fig. 11
figure 11

Solution sets obtained by SMS-EMOA with different \(\sigma \) on the three-objective MOP-CH

Full size image

Figure 6 presents the obtained solution set with the median HV value in the 30 runs of each algorithm on the three-objective MOP-CH. It can be seen from Fig. 6a that NSGA-II suffers from DRSs and fail to approximate the PF. Figure 6b shows that MOEA/D-PBI gains many solutions around the center of the PF. However, it misses many solutions around the three corners of the PF. Figure 6c indicates that the solution set yielded by MOEA/D-Gen approximates the PF well, whereas several DRSs also exist in the set. In Fig. 6d, we can find that \(\epsilon \)-MOEA keeps quite a number of DRSs. As shown in Fig. 6e, no DRS is in the solution set obtained by mNSGA-II. However, almost all solutions are around the center of the PF. Figure 6f reveals that the best approximation set is obtained by SMS-EMOA. However, many solutions are not obtained around the boundary of the PF. All in all, we can see that all the examined six MOEAs miss the boundary solution while some MOEAs cannot eliminate the DRS perfectly.

Parameter analysis

According to [12, 24], the performance of the MOEAs may be affected by the parameters. Therefore, the parameter analysis is conducted on MOEA/D-PBI, MOEA/D-Gen, \(\epsilon \)-MOEA, mNSGA-II and SMS-EMOA. Figures 7, 8, 9, 10 and 11 show the solutions obtained by these algorithms, respectively.

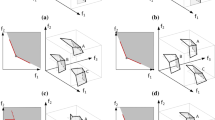
Figure 7 shows the solution sets obtained by MOEA/D-PBI with \(\theta \) = 2, 10 and 15 on the three-objective MOP-CH. With the increase of \(\theta \), the distribution of the obtained solutions becomes wider, and more boundary solutions are preserved. Nevertheless, the number of DRSs increases at the same time. In Fig. 7b, c, we can see that more DRSs are retained while gaining more boundary solutions of the ECPF. This indicates that MOEA/D-PBI with a large value of \(\theta \) may misjudge the merits of the DRS and the boundary solution of the ECPF, and preserve DRSs instead of boundary solutions.

This figure presents the solution sets obtained by mNSGA-II with \(\alpha = 0.001, 0.01\) and 0.2 on the three-objective MOP-CH. Similar to \(\epsilon \)-MOEA when \(\alpha \) is very small, the convergence of mNSGA-II is severely deteriorated by DRSs. With the increase of \(\alpha \), DRSs in the obtained solution sets become less, and more solutions are located over the PF. However, when the value of \(\alpha \) is too large, all solutions are around the center of the PF. mNSGA-II also suffers from the dilemma between the DRS elimination and the boundary solutions preservation.

Figure 8 presents the solution sets obtained by MOEA/D-Gen with \(\rho \) = 0.05, 0.005 and 0.0001 on the three-objective MOP-CH. By decreasing the value of \(\rho \), MOEA/D-Gen can get more widely distributed solutions over the PF. However, the PF is not approximated well even when a very small value is used in MOEA/D-Gen. Besides, it is noteworthy that DRSs are not eliminated completely by MOEA/D-Gen with any of the three \(\rho \) settings. This indicates that MOEA/D-Gen is also caught in the dilemma between the DRS elimination and the boundary solution preservation.

Figure 9 shows the solution sets obtained by \(\epsilon \)-MOEA with \(\epsilon \) = 0.01, 0.05 and 0.1 on the three-objective MOP-CH. The number of the obtained solutions by \(\epsilon \)-MOEA is related to the value of \(\epsilon \). The larger the value of \(\epsilon \), the less the number of the obtained solutions. It can be seen that the DRSs can be eliminated from the solution set by increasing the value of \(\epsilon \), which leads to the severe decrease in the number of obtained solutions as shown in Fig. 9c. Moreover, almost all of these solutions are located around the center of the PF. Boundary solutions of the PF are missing.

As shown in Fig. 6f, when \(\sigma = 1,\) most of the obtained solutions are located around the center of the PF. Here we test SMS-EMOA with \(\sigma = 3, 5\) and 10 on the three-objective MOP-CH. Figure 11 presents the obtained solutions in the objective space with each parameter setting. When \(\sigma = 10,\) many obtained solutions are located on the boundaries of the PF. In the case of \(\sigma = 3,\) SMS-EMOA cannot find some boundary solutions of the PF. SMS-EMOA with \(\sigma = 5\) achieves the best performance on the three-objective MOP-CH. From these result, we can conclude that the value of \(\sigma \) can affect the distribution of the obtained solutions. A large \(\sigma \) benefits SMS-EMOA to achieve more boundary solutions, while a small \(\sigma \) promotes SMS-EMOA to obtain more solutions around the centre of the PF. Only by setting \(\sigma \) very carefully can SMS-EMOA obtain approximate solutions with the perfect distribution.

Based on the above mentioned results, it can be concluded that the performance of these MOEAs is very sensitive to their parameters. All the algorithms except for SMS-EMOA are trapped in the dilemma between the DRS elimination and the boundary solution preservation. SMS-EMOA has a different type of dilemma in terms of the population uniformity. Moreover, SMS-EMOA is hindered by its huge calculation time on the many-objective MOPs. The experimental results also reveal that it is hard for the MOEA to distinguish between DRSs and boundary solutions of the ECPF.

Conclusion

In this paper, we have explained how DRSs degrade the performance of MOEAs and how five MOEAs can eliminate DRSs. Then, we have discussed the dilemma between the DRS elimination and the boundary solution preservation. We have used a two-objective MOP as an example to illustrate such a dilemma. In addition, we have proposed a new MOP (named as MOP-CH) with the ECPF and DRSs. Six representative MOEAs have been applied to the proposed problem to examine their performance in terms of eliminating DRSs and preserving boundary solutions of the ECPF. Our experimental results have shown that NSGA-II suffers from DRSs and fails to approximate the PF. The MOEAs with DRS eliminating strategies are caught in the dilemma between the DRS elimination and the boundary solution preservation. The results have also shown that the hypervolume-based MOEA is most promising in getting rid of such a dilemma. However, its calculation time will be a heavy burden when the MOP has many objective functions. Furthermore, when the PF shape is irregular, it is challenging for SMS-EMOA to get uniformly distributed solutions (including boundary solutions).

In the future, we will study how to distinguish between DRSs and boundary solutions of the ECPF and how to balance between the DRS elimination and the boundary solution preservation. More test problems with DRSs and various types of ECPFs will be developed as well.