Introduction

A control chart is an important tool of statistical process control for maintaining and improving the quality of the product to compete in the market [1]. An efficient control chart is one, which quickly indicates any special cause of variation in the process so that the engineers can take immediate action to remove the fault and avoid the burden of rework and defective items. This objective can only be achieved if we have complete, crisp, and authentic information/data about the manufacturing unit under study. Life testing experiments are very common in the statistical process control literature when a random sample of items is selected and put on testing for possible failure [2]. The sudden death testing is repeatedly applied by many parts manufacturers with the objective of reduced time of test, see [3]. In this technique, a sample of items is first spread in \(g\) groups with each group having \(r\) items. Sudden death testing in groups is preferred over the single tester as it reduces the testing cost of the product. Sudden death testing technique has been explored by many quality control researchers including [3,4,5,6]. It is common to use the Weibull distribution for modeling lifetime phenomena. The density function of the Weibull distribution is typically written as

$$ P\left( x \right) = \frac{m}{\lambda } \left( {\frac{x}{\lambda }} \right)^{m - 1} {\text{exp}}\left[ { - \left( {\frac{x}{\lambda }} \right)^{m} } \right]; > 0,\;m\; {\text{and}}\;\lambda > 0 $$
(1)

where \(\lambda\) and \(m\) are the scale and shape parameters, respectively. When the shape parameter is one, then this distribution tends to form the exponential distribution. The Weibull distribution has been explored by many quality control researchers including [7] developed life-testing sampling plan for the two-parameter Weibull distribution, [8] developed bootstrap control chart for Weibull percentiles, [3] developed a variables sampling plans for Weibull distributed lifetimes under sudden death testing, [9] given progressively censored reliability sampling plans for the Weibull distribution, [10] suggested a group acceptance sampling plan for truncated life test having Weibull distribution, [11] developed acceptance sampling plans for multi-stage process based on a time-truncated test for Weibull distribution.

Average run length (ARL) is a traditionally used technique in the literature of the control charts for evaluating the efficiency of the proposed control chart [1]. It is defined as the average number of samples when the process is in control until the process falsely shows an out-of-control signal and is denoted by \({\mathrm{ARL}}_{0}\), see [12]. To keep the level of \({\mathrm{ARL}}_{0}\) at an acceptable level, it should be large enough. Another characteristic of ARL is used for the out-of-control process which should be smaller enough for the efficient control chart scheme and is denoted by \({\mathrm{ARL}}_{1}\). ARL for the evaluation of a better control chart scheme has been used by many authors including [13,14,15,16,17,18,19,20,21,22,23,24].

In practice, however, the observations about the manufacturing process are imprecise, incomplete, uncertain, or fuzzy [25]. Fuzzy-based control charts are applied in industry for the monitoring of the process when some observations/parameters are unknown or imprecise. The traditional control chart based on the assumption that all observations should be determined cannot be applied for the process monitoring when some values are fuzzy. Several authors contributed in this area by designing a fuzzy control chart for various situations, see for example, [26,27,28,29,30,31,32,33,34, 35]. More details can be seen in [36].

[37] developed the notion of neutrosophic statistics (NS) using the idea of neutrosophic logic was given by Smarandache [38]. The difference between fuzzy logic and neutrosophic logic can be seen in [39]. [40,41,42] discussed neutrosophic logic in a variety of fields. The neutrosophic statistics is applied when the data in hand are uncertain, imprecise, and indeterminate. The neutrosophic statistics is more informative than classical statistics. The neutrosophic statistics gives the information about the measure of indeterminacy. In addition, it gives the estimated values in the indeterminate intervals which are required in uncertain environment, see [37]. Several authors studied the neutrosophic statistics including [43] used the neutrosophic interval statistical numbers for expressions rock joint roughness coefficients, [44] studied the anisotropy for neutrosophic numbers of rock joint roughness using the neutrosophic statistics, [2] proposed a plan for neutrosophic statistics for testing of grouped product using the Weibull distribution, [45] developed the monitoring methodology for process variability using the neutrosophic statistics, [46] developed a sampling plan using the neutrosophic regression estimator. Recently, [47] introduced the NS in the area of statistical quality control. [45, 48, 49] proposed attribute np, X-bar, and variance control charts using NS, respectively. More details on NS-based control charts can be seen in [50, 51].

[2] designed the sudden death sampling plan using the NS. By exploring the literature and to the best of our knowledge, there is no work on the control sudden death control chart for monitoring the process of having incomplete, imprecise, and vague production data. In this paper, we will propose the sudden death control chart for monitoring the reliability when the lifetime of the product follows the Weibull distribution under the uncertainty environment. We will present some necessary measures to evaluate the performance of the proposed control chart under the neutrosophic statistical interval method (NSIM). We hope that the proposed control chart will be more adequate, adequate, and informative than the sudden death chart under classical statistics in an uncertain environment. The rest of the paper is organized as follows: the design of the proposed chart is given in "Design of proposed control chart". The advantages of the proposed chart are given in "Advantages of the proposed control chart". In "Example", an example is given and some concluding remarks are given in the last section.

Design of proposed control chart

Suppose that \(X_{{\text{N}}} = X + uI\); \(I \in \left[ {\text{inf,sup}} \right]\) be a neutrosophic random variable having a variable \(X\) under classical statistics (determinate part) and \(uI\);\( I \in \left[ {\text{inf,sup}} \right]\) is a indeterminate part. Let \(X_{{\text{N}}} \in \left[ {X_{{\text{L}}} ,X_{{\text{U}}} } \right]\) denote the lifetime of a part, where \(X_{{\text{L}}}\) is lower value of indeterminacy interval and \(X_{{\text{U}}}\) be the upper value of the indeterminacy interval, which follows, the neutrosophic Weibull distribution with neutrosophic scale parameter \(\lambda_{{\text{N}}} \in \left[ {\lambda_{{\text{L}}} ,\lambda_{{\text{L}}} } \right]\) and neutrosophic shape parameter \(m_{{\text{N}}} \in \left[ {m_{{\text{L}}} ,m_{{\text{L}}} } \right]\), then the cumulative distribution function can be written as:

$$ F\left( {x_{{\text{N}}} } \right) = 1 - {\text{exp}}\left( { - \left( {\lambda_{{\text{N}}} x_{{\text{N}}} } \right)^{{m_{{\text{N}}} }} } \right);\;m_{{\text{N}}} \in \left[ {m_{{\text{L}}} ,m_{{\text{L}}} } \right],{ }\lambda_{{\text{N}}} \in \left[ {\lambda_{{\text{L}}} ,\lambda_{{\text{L}}} } \right] $$
(2)

The operational procedure of the proposed neutrosophic control chart for monitoring reliability using sudden death testing under Weibull distribution is stated as follows:

Step-1 Select a random sample of size \(n_{{\text{N}}}\);\({ }n_{{\text{N}}} \in \left[ {n_{{\text{L}}} ,n_{{\text{U}}} } \right]\) having neutrosophic numbers from a manufacturing process and distribute \(r_{{\text{N}}}\);\({ }r_{{\text{N}}} \in \left[ {r_{{\text{L}}} ,r_{{\text{U}}} } \right]\) items into \(g_{{\text{N}}}\);\({ }g_{{\text{N}}} \in \left[ {g_{{\text{L}}} ,g_{{\text{U}}} } \right]\) groups having \(n_{{\text{N}}} = r_{{\text{N}}} g_{{\text{N}}}\).

Step-2 Perform sudden death testing and detect \( Y_{iN}\), the time to the first failure from the ith group \(\left( {i = 1,2, \ldots g_{{\text{N}}} } \right)\) and compute the value \(v_{{\text{N}}} = \mathop \sum \nolimits_{i = 1}^{{g_{{\text{N}}} }} Y_{{i{\text{N}}}}^{{m_{{\text{N}}} }}\);\( v_{{\text{N}}} \in \left[ {v_{{\text{L}}} ,v_{{\text{U}}} } \right]\) and convert it to \(v_{{\text{N}}}^{*} = v_{{\text{N}}}^{{1/3}}\); \( v_{{\text{N}}}^{*} \in \left[ {v_{{\text{L}}}^{*} {,}v_{{\text{U}}}^{*} } \right]\).

Step-3 Plot \(v_{N}^{*}\) on the control chart. Declare the process in-control if \({\text{LCL}}_{{\text{N}}}^{{1/3}} \;{ < }\;v_{{\text{N}}}^{*} \;{ < }\;{\text{UCL}}_{{\text{N}}}^{{1/3}}\). If \(v_{{\text{N}}}^{*} \le {\text{LCL}}_{{\text{N}}}^{{1/3}} {\text{or }}v_{{\text{N}}}^{*} \ge {\text{UCL}}_{{\text{N}}}^{{1/3}}\), then declare the process out-of-control. Two control limits, namely \({\text{LCL}}_{{\text{N}}}^{{1/3}}\);\( {\text{LCL}}_{{\text{N}}}^{{1/3}} \in \left[ {{\text{LCL}}_{{\text{L}}}^{{1/3}} {,}\;{\text{LCL}}_{{\text{U}}}^{{1/3}} } \right]\) and \({\text{UCL}}_{{\text{N}}}^{{1/3}}\);\( {\text{UCL}}_{{\text{N}}}^{{1/3}} \in \left[ {{\text{UCL}}_{{\text{L}}}^{{1/3}} {,}\;{\text{UCL}}_{{\text{U}}}^{{1/3}} } \right]\), for the proposed control chart have been constructed.

Following Jun et al. [3], the quantity \(v_{{\text{N}}} \in \left[ {v_{{\text{L}}} ,v_{{\text{U}}} } \right]\) follows the neutrosophic Weibull distribution with shape parameter \(g_{{\text{N}}} \in \left[ {g_{{\text{L}}} ,g_{{\text{U}}} } \right]\) and scale parameter \(r_{{\text{N}}} \lambda_{{\text{N}}}^{{m_{{\text{N}}} }}\). For developing symmetric Shewhart-type control limits, we must transform \(v_{{\text{N}}} \in \left[ {v_{{\text{L}}} ,v_{{\text{U}}} } \right]\) into a random variable having a neutrosophic symmetric distribution. [52] mentioned that transformation of \(v_{{\text{N}}}^{*} = v_{{\text{N}}}^{{1/3}}\) leads to an approximately neutrosophic normal distribution with neutrosophic mean

$$ \mu_{{{\text{v}}^{*} {\text{N}}}} = \frac{{\left( {r_{{\text{N}}} \lambda_{{\text{N}}}^{{m_{{\text{N}}} }} } \right)^{1/3} {\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }1/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}};\,\, \mu_{{{\text{v}}^{*} {\text{N}}}} \in \left[ {\mu_{{{\text{v}}^{*} {\text{L}}}} ,\mu_{{{\text{v}}^{*} {\text{U}}}} } \right] $$
(3)

And neutrosophic variance

$$ \sigma_{{{\text{v}}^{*} {\text{N}}}}^{{2}} = \frac{{\left( {r_{{\text{N}}} \lambda_{{\text{N}}}^{{m_{{\text{N}}} }} } \right)^{2/3} {\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} - \left( {\mu_{{{\text{v}}^{*} {\text{N}}}} } \right)^{2} ;\,\,\sigma_{{{\text{v}}^{*} {\text{N}}}}^{{2}} \in \left[ {\sigma_{{{\text{v}}^{*} {\text{L}}}}^{{2}} ,\sigma_{{{\text{v}}^{*} {\text{U}}}}^{{2}} } \right] $$
(4)

where \({\Gamma }_{{\text{N}}} \left( x \right)\) denotes the neutrosophic gamma function.

Therefore, the control limits for the proposed control chart are given as:

$$ {\text{LCL}}_{{\text{N}}} = \frac{{\left( {r_{{\text{N}}} \lambda_{{{\text{0N}}}}^{{m_{{\text{N}}} }} } \right)^{1/3} \Gamma \left( {g_{{\text{N}}} + 1/3} \right)}}{{\Gamma_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} - k_{{\text{N}}} \sqrt {\frac{{\left( {r_{{\text{N}}} \lambda_{{\text{N}}}^{{m_{{\text{N}}} }} } \right)^{2/3} \Gamma_{{\text{N}}} \left( {g_{{\text{N}}} + 2/3} \right)}}{{\Gamma_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} - \left( {\mu_{{{\text{v}}^{*} {\text{N}}}} } \right)^{2} } $$
(5)
$$ \begin{aligned} {\text{LCL}}_{{\text{N}}}^{{1/3}} &= r_{{\text{N}}} \lambda_{{{\text{0N}}}}^{{m_{{\text{N}}} }} \left\{ \frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }1/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}}\right.\\ &\quad\left.- k_{{\text{N}}} \sqrt {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} - \left( {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}}} \right)^{2} } \right\} \end{aligned} $$
(6)
$$ {\text{UCL}}_{{\text{N}}} = \frac{{\left( {r_{{\text{N}}} \lambda_{{{\text{0N}}}}^{{m_{{\text{N}}} }} } \right)^{1/3} {\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} + 1/3} \right)}}{{\Gamma_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} + k_{{\text{N}}} \sqrt {\frac{{\left( {r_{{\text{N}}} \lambda_{{\text{N}}}^{{m_{{\text{N}}} }} } \right)^{2/3} \Gamma_{{\text{N}}} \left( {g_{{\text{N}}} + 2/3} \right)}}{{\Gamma_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} - \left( {\mu_{{{\text{v}}^{*} {\text{N}}}} } \right)^{2} } $$
(7)
$$ \begin{aligned} {\text{UCL}}_{{\text{N}}}^{{1/3}} &= r_{{\text{N}}} \lambda_{{{\text{0N}}}}^{{m_{{\text{N}}} }} \left\{ \frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }1/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} \right.\\ &\quad\left.+ k_{{\text{N}}} \sqrt {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} - \left( {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}}} \right)^{2} } \right\} \end{aligned} $$
(8)

Note here that \(k_{{\text{N}}} \in \left[ {k_{{\text{L}}} ,k_{{\text{U}}} } \right]\) is neutrosophic control limits coefficient and \(\lambda_{{{\text{0N}}}}\) is the neutrosophic scale parameter of the in-control process.

For the proposed control chart, the process is declared to be out-of-control if \(v_{{\text{N}}}^{*} \left\langle {{\text{LCL}}_{{\text{N}}}^{{1/3}} {\text{or }}v_{{\text{N}}}^{*} } \right\rangle {\text{UCL}}_{{\text{N}}}^{{1/3}}\). Therefore, the probability that the process is declared as out-of-control when the process is actually in-control is given as follows:

$$ P_{{{\text{outN}}}}^{0} = P{ }\left\{ {{ }v_{{\text{N}}}^{*} { }\left\langle { {\text{LCL}}_{{\text{N}}}^{{1/3}} } \right|\lambda_{{0{\text{N}}}} } \right\} + P \left\{ {v_{{\text{N}}}^{*} { } > {\text{UCL}}_{{\text{N}}}^{{1/3}} |\lambda_{{0{\text{N}}}} } \right\} $$
(9)

where

$$ P \left\{ {{ }v_{{\text{N}}}^{*} { }\; < \;{\text{ LCL}}_{{\text{N}}}^{{1/3}} {|}\lambda_{{0{\text{N}}}} } \right\} = P\left\{ {2r_{{\text{N}}} \lambda_{{\text{N}}}^{{m_{{\text{N}}} }} v_{{\text{N}}}^{*} \left\langle {2r_{{\text{N}}} \lambda_{{\text{N}}}^{{m_{{\text{N}}} }} {\text{LCL}}_{{\text{N}}}^{{1/3}} } \right|\lambda_{{0{\text{N}}}} } \right\} $$

or

$$ \begin{aligned} &P{ }\left\{ {{ }v_{{\text{N}}}^{*} { } < {\text{LCL}}_{{\text{N}}}^{{1/3}} {|}\lambda_{{0{\text{N}}}} } \right\} = G_{{{\text{2gN}}}} \left( 2\left( {r_{{\text{N}}} \lambda_{{0{\text{N}}}}^{{m_{{\text{N}}} }} } \right)^{2} \left\{ \frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }1/3} \right)}}{{{\Gamma }\left( {g_{{\text{N}}} } \right)}}\right.\right.\\ &\quad\left.\left.- k_{{\text{N}}} \sqrt {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} - \left( {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}}} \right)^{2} } \right\} \right) \end{aligned} $$

and

$$ \begin{aligned} &P \left\{ { v_{{\text{N}}}^{*} { } > {\text{ UCL}}_{{\text{N}}}^{{1/3}} {|}\lambda_{{0{\text{N}}}} } \right\} = 1 - G_{{{\text{2gN}}}} \left( 2\left( {r_{{\text{N}}} \lambda_{{{\text{0N}}}}^{{m_{{\text{N}}} }} } \right)^{2} \left\{ \frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }1/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}}\right.\right.\\ &\quad\left.\left.+ k_{{\text{N}}} \sqrt {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} - \left( {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}}} \right)^{2} } \right\} \right) \end{aligned} $$

So, the average run length (ARL) using the neutrosophic statistical interval method (NSIM) is known as the neutrosophic average run length (NARL) is denoted by \(ARL_{N}\) which was introduced by [45] as follows:

$$ {\text{ARL}}_{{{\text{0N}}}} = \frac{1}{{P_{{{\text{outN}}}}^{{0}} }}; {\text{ARL}}_{{{\text{0N}}}} \in\,\, \left[ {{\text{ARL}}_{{{\text{0L}}}} {,}\;\;{\text{ARL}}_{{{\text{0U}}}} } \right] $$
(10)

When the process faces a shift, then the NARL is denoted by \(ARL_{1N}\), then

$$ P_{{{\text{out}}1{\text{N}}}}^{0} = { }P{ }\left\{ {{ }v_{{\text{N}}}^{*} \left\langle {{\text{LCL}}_{{\text{N}}}^{{1/3}} { }} \right|\lambda_{{1{\text{N}}}} = c\lambda_{{0{\text{N}}}} } \right\} + P \left\{ {v_{{\text{N}}}^{*} > {\text{UCL}}^{3} |\lambda_{{1{\text{N}}}} = c\lambda_{{0{\text{N}}}} } \right\} $$
(11)

where

$$ P{ }\left\{ {{ }v_{{\text{N}}}^{*} { } < {\text{LCL}}_{N}^{1/3} {|}\lambda_{{0{\text{N}}}} } \right\} = P\left\{ {2r_{{\text{N}}} \lambda_{1}^{m} v\left\langle {2r\lambda_{1}^{m} {\text{LCL}}_{{\text{N}}}^{{1/3}} } \right|\lambda_{{1{\text{N}}}} } \right\} $$

or

$$ \begin{aligned} &{\text{P }}\left\{ {{ }v_{{\text{N}}}^{*} { } < {\text{LCL}}_{{\text{N}}}^{{1/3}} {|}\lambda_{{1{\text{N}}}} } \right\} = G_{{{\text{2gN}}}} \left( 2c^{{m_{{\text{N}}} }} r_{{\text{N}}}^{{2}} {\uplambda }_{{0{\text{N}}}}^{{2m_{{\text{N}}} }} \left\{ \frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }1/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}}\right.\right.\\ &\quad\left.\left.- k_{{\text{N}}} \sqrt {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} - \left( {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}}} \right)^{2} } \right\} \right) \end{aligned} $$

and

$$ \begin{aligned} &P \left\{ { v_{{\text{N}}}^{*} { } > {\text{UCL}}^{3} {|}\lambda_{1} } \right\} = 1 - G_{{{\text{2gN}}}} \left( 2c^{{m_{{\text{N}}} }} r_{{\text{N}}}^{{2}} \lambda_{{0{\text{N}}}}^{{2m_{{\text{N}}} }} \left\{ \frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }1/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}}\right.\right.\\ &\quad\left.\left.+ k_{N} \sqrt {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}} - \left( {\frac{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} { } + { }2/3} \right)}}{{{\Gamma }_{{\text{N}}} \left( {g_{{\text{N}}} } \right)}}} \right)^{2} } \right\} \right) \end{aligned} $$

Therefore, the neutrosophic average run length for the shifted process is given by

$$ {\text{ARL}}_{{{\text{1N}}}} = \frac{1}{{{\text{P }}\left\{ {{ }v_{{\text{N}}}^{*} \left\langle {{\text{LCL}}_{{\text{N}}}^{{1/3}} } \right|\lambda_{{{\text{1N}}}} = c\lambda_{{0{\text{N}}}} } \right\} + P \left\{ {v_{{\text{N}}}^{*} > {\text{UCL}}^{3} |\lambda_{{1{\text{N}}}} = c\lambda_{{0{\text{N}}}} } \right\}}};{\text{ ARL}}_{{{\text{1N}}}} \in \left[ {{\text{ARL}}_{{{\text{1L}}}} {\text{,ARL}}_{{{\text{1U}}}} } \right] $$
(12)

Let \(d_{{{\text{0N}}}} \in \left[ {d_{{{\text{0L}}}} ,d_{{{\text{0U}}}} } \right]\) denotes the specified NARL. The values of \(k_{{\text{N}}} \in \left[ {k_{{\text{L}}} ,k_{{\text{U}}} } \right]\) will be determined such that \({\text{ARL}}_{{{\text{0N}}}} \in \left[ {{\text{ARL}}_{{{\text{0L}}}} {\text{,ARL}}_{{{\text{0U}}}} } \right]\) should be very close to \(d_{{{\text{0N}}}} \in \left[ {d_{{{\text{0L}}}} ,d_{{{\text{0U}}}} } \right]\). The values of \({\text{ARL}}_{{{\text{1N}}}} \in \left[ {{\text{ARL}}_{{{\text{1L}}}} {\text{,ARL}}_{{{\text{1U}}}} } \right]\) for various values of \(m_{{\text{N}}} \in \left[ {m_{{\text{L}}} ,m_{{\text{L}}} } \right]\) \(r_{{\text{N}}} \in \left[ {5,5} \right]\),\({ }\lambda_{{\text{N}}} \in \left[ {\lambda_{{\text{L}}} ,\lambda_{{\text{L}}} } \right]\) and \(d_{{{\text{0N}}}} \in \left[ {d_{{{\text{0L}}}} ,d_{{{\text{0U}}}} } \right]\) are determined and are shown in Tables 1, 2, 3 and 4. From Tables 1, 2, 3 and 4, we note the following trend in neutrosophic parameters.

  1. 1.

    For all other the same neutrosophic parameters, the values of \({\text{ARL}}_{{{\text{1N}}}} \in \left[ {{\text{ARL}}_{{{\text{1L}}}} {\text{,ARL}}_{{{\text{1U}}}} } \right]\) increase when \(\lambda_{{\text{N}}} \in \left[ {\lambda_{{\text{L}}} ,\lambda_{{\text{L}}} } \right]\) increases from \(\lambda_{{\text{N}}} \in \left[ {0.5,0.5} \right]\) to \(\lambda_{{\text{N}}} \in \left[ {1,1} \right]\).

  2. 2.

    For all other the same neutrosophic parameters, the values of \({\text{ARL}}_{{{\text{1N}}}} \in \left[ {{\text{ARL}}_{{{\text{1L}}}} {\text{,ARL}}_{{{\text{1U}}}} } \right]\) decrease when \(\lambda_{{\text{N}}} \in \left[ {\lambda_{{\text{L}}} ,\lambda_{{\text{L}}} } \right]\) increases from \(\lambda_{{\text{N}}} \in \left[ {1.5,1.5} \right]\) to \(\lambda_{{\text{N}}} \in \left[ {2.0,2.0} \right]\).

  3. 3.

    From the above observations, we note the increasing the trend in \({\text{ARL}}_{{{\text{1N}}}} \in \left[ {{\text{ARL}}_{{{\text{1L}}}} {\text{,ARL}}_{{{\text{1U}}}} } \right]\) when \(\lambda_{{\text{N}}} \in \left[ {\lambda_{{\text{L}}} ,\lambda_{{\text{L}}} } \right] \le 1\) and decreasing trend when \(\lambda_{{\text{N}}} \in \left[ {\lambda_{{\text{L}}} ,\lambda_{{\text{L}}} } \right] > 1\).

  4. 4.

    From these Tables 1, 2, 3 and 4, it can be seen that the value of ARLN decreases as the shifts from 1.0 to 6.0 increases.

Table 1 The values of NARL when \(r_{{\text{N}}} \in \left[ {5,5} \right]\), \(m_{{\text{N}}} \in \left[ {2,2.1} \right]\) and various \( {\text{ARL}}_{{{\text{1N}}}}\)
Full size table
Table 2 The values of NARL when \(r_{{\text{N}}} \in \left[ {5,5} \right]\), \(m_{{\text{N}}} \in \left[ {0.85,0.95} \right]\) and various \( {\text{ARL}}_{{{\text{1N}}}}\)
Full size table
Table 3 The values of NARL when \(r_{{\text{N}}} \in \left[ {5,5} \right]\), \(m_{{\text{N}}} \in \left[ {1.45,1.55} \right]\) and various \({\text{ ARL}}_{{{\text{1N}}}}\)
Full size table
Table 4 The values of NARL when \(r_{{\text{N}}} \in \left[ {5, 5} \right]\), \(m_{{\text{N}}} \in \left[ {2.1,2.3} \right]\) and various \( {\text{ARL}}_{{{\text{1N}}}}\)
Full size table

The following algorithm is used to find the values of \(k_{{\text{N}}} \in \left[ {k_{{\text{L}}} ,k_{{\text{U}}} } \right]\) and \({\text{ARL}}_{{{\text{1N}}}} \in \left[ {{\text{ARL}}_{{{\text{1L}}}} {\text{,ARL}}_{{{\text{1U}}}} } \right]\).

Step-1: determine the suitable range of \(k_{{\text{N}}} \in \left[ {k_{{\text{L}}} ,k_{{\text{U}}} } \right]\) and prefix the values of \(d_{{{\text{0N}}}} \in \left[ {d_{{{\text{0L}}}} ,d_{{{\text{0U}}}} } \right]\), \(m_{{\text{N}}} \in \left[ {m_{{\text{L}}} ,m_{{\text{L}}} } \right]\) and \(\lambda_{{\text{N}}} \in \left[ {\lambda_{{\text{L}}} ,\lambda_{{\text{L}}} } \right]\).

Step-2: Determine the values \(k_{{\text{N}}} \in \left[ {k_{{\text{L}}} ,k_{{\text{U}}} } \right]\) such that \({\text{ARL}}_{{{\text{0N}}}} \ge d_{{{\text{0N}}}}\). During the simulation, we note that several combinations are available which satisfy the given condition. Select those values of \(k_{{\text{N}}} \in \left[ {k_{{\text{L}}} ,k_{{\text{U}}} } \right]\), where \({\text{ARL}}_{{{\text{0N}}}} \in \left[ {{\text{ARL}}_{{{\text{0L}}}} {\text{,ARL}}_{{{\text{0U}}}} } \right]\) is very close to \(d_{0N} \in \left[ {d_{0L} ,d_{0U} } \right]\).

Step-3: Using the selected values of \(k_{{\text{N}}} \in \left[ {k_{{\text{L}}} {,}k_{{\text{U}}} } \right]\), determine the values of \({\text{ARL}}_{{{\text{1N}}}} \in \left[ {{\text{ARL}}_{{{\text{1L}}}} {\text{,ARL}}_{{{\text{1U}}}} } \right]\) for various \(c\).

Advantages of the proposed control chart

In this section, we will discuss the advantages of the proposed control chart under neutrosophic statistics over the existing control chart under classical statistics proposed by [53]. [43, 44] mentioned that a method which provides the output in indeterminate interval under uncertainty is known as the most an effective and adequate method. To compare the proposed chart with [53], we will fix the same values of the control chart parameters. The values of NARL of the proposed control chart and [53] chart are shown in Table 5 for various values of control chart parameters.

Table 5 The comparison in NARL
Full size table

From Table 5, it can be noted that all values of [53] chart are within the indeterminacy interval of the proposed control chart. The NARL values of the proposed control chart become the same as in [53] if no uncertain observation is recorded in the data. For example, when \(c\) = 1.1 and \( \lambda_{{\text{N}}} \in \left[ {2,2} \right]\), the indeterminacy interval of NARL for the proposed chart is from 172nd sample to the 317th sample. It means that one can expect that the proposed control chart indicates that on average, the process will be shifted between 172nd to 317th samples. On the other hand, [53] indicates that the first out-of-control will be detected at the 317th sample. From this study, it can be seen that the proposed chart gives smaller values of NARL as compared to the existing chart. In addition, from this comparison, it is clear that the proposed control chart gives the results in indeterminate interval; therefore, it is flexible, informative, and adequate and concurs with the theory of [43, 44]. Hence, the proposed control chart under neutrosophic statistics is a better alternative of [53] chart under classical statistics when there is Neutrosophy in the data.

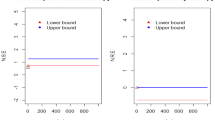
Now, we present the efficiency of the proposed control chart over [53] using the simulated data. Using the neutrosophic Weibull distribution, the neutrosophic data were generated in which the first 20 observations belong to the in-control process while the next 20 observations from the shifted process with \(c\) = 2.0. Now according to Table 3, \({\text{ARL}}_{{{\text{1N}}}} \in \left[ {55.21,12.02} \right]\) when \( k_{{\text{N}}} \in \left[ {2.981687,3.86765} \right]\),\(\lambda_{{\text{N}}} \in \left[ {0.45,0.55} \right], g_{{\text{N}}} \in \left[ {2,4} \right]\) and \(m_{{\text{N}}} \in \left[ {1.45,1.55} \right]\). According to the proposed chart, it can be expected a shift between 55th sample and 12th sample. The values of statistic \(v_{{\text{N}}}^{*} \in \left[ {v_{{\text{L}}}^{*} ,v_{{\text{U}}}^{*} } \right]\) are plotted in Fig. 1 for the proposed chart and in Fig. 2 for [53] chart under classical statistics. We note from Fig. 1 that the 29th sample is at the neutrosophic lower limit which indicates that the process has shifted. From the figure, it can be seen that all plotting values are within the control limits and do not show any shift in the process. From Figs. 1, 2, it is clear that the proposed control chart detects a shift in the process at the 29th sample while the existing control chart indicates that the process is an in-control state. Figure 2 also shows several values of \(v_{{\text{N}}}^{*} \in \left[ {v_{{\text{L}}}^{*} ,v_{{\text{U}}}^{*} } \right]\) within the indeterminacy interval. From this comparison, it is quite clear that the proposed chart has the ability to detect a shift in the process.

Fig. 1
figure 1

The proposed chart for the simulated data

Full size image
Fig. 2
figure 2

[53] chart for the simulated data

Full size image

Example

Suppose that a ball bearing company is interested to apply the proposed control chart for the monitoring of the ball bearing reliability. The company found that the reliability data follow the neutrosophic Weibull distribution with \({m}_{\mathrm{N}}\epsilon [\mathrm{2.1,2.3}]\) and \({\lambda }_{\mathrm{N}}\epsilon [\mathrm{0.55,0.65}]\). For this experiment, let \({r}_{\mathrm{N}}\epsilon \left[5,5\right]\) and \({\mathrm{ARL}}_{1\mathrm{N}}\epsilon \left[370,370\right]\). For these parameters, \({g}_{\mathrm{N}}\epsilon \left[4,4\right]\) from Table 4. The experimenter will select a random sample of 20 balls and distribute them into 4-subgroup size. During the experiment, it is found that the reliability values of ball bearing are neutrosophic numbers rather than the exact numbers. Therefore, the monitoring of the process will be done using the proposed control chart. The neutrosophic data are shown in Table 6.

Table 6 The \(m_{\rm N} = \left[ {2.1,2.3} \right]\), \(\lambda_{\rm N} = \left[ {0.55,0.65} \right]\) in-control process data generated from Weibull distribution
Full size table

The values of statistic \({v}_{\mathrm{N}}^{*}\epsilon \left[{v}_{\mathrm{L}}^{*},{v}_{\mathrm{U}}^{*}\right]\) are plotted in Fig. 3 for the proposed control chart and in Fig. 4 for the existing control chart proposed by [53] under classical statistics. From Figs. 3, 4, we note that the proposed control chart provides the values in indeterminacy interval rather than the exact values. In addition, the proposed control chart shows that three plotting statistics are near the control limit which should be a problem in the process.

Fig. 3
figure 3

The proposed chart for ball bearing data

Full size image
Fig. 4
figure 4

The existing chart for the ball bearing data

Full size image

Conclusion

In this article, a neutrosophic control chart for monitoring the reliability using sudden death testing under Weibull distribution has been presented. The NSIM has been used for the required measures to apply the proposed control chart. A simulation study was made to show the comparative efficiency of the proposed chart for the uncertainty environment. From the comparative study, it was noted that the proposed chart is efficient than the existing chart. In addition, on comparing the proposed chart, it can be observed that it is adequate, more flexible, and more efficient for use in an uncertain environment. In nutshell, the proposed chart is a valuable addition in the toolkit of the quality control personnel when there are unclear, uncertain, vague, or fuzzy observations in the sample. The proposed chart can be extended for the cost models or some other sampling schemes as future research.