Introduction

The processing and application of the original high-dimensional data are very challenging. To address this problem, many data dimensionality reduction methods were applied to solve image retrieval image indexing [1, 2] and image classification [3]. To achieve a satisfactory subspace from dimensionality reduction, most of the studies mainly consider how to discover an effective low-dimensional representation from the original data. A common scheme is to dig out the geometrical structure information of the original data, which can lead to a more discriminative representation.

In the past decades, several dimensionality reduction techniques were presented such as principal components analysis (PCA) [4] and non-negative matrix factorization (NMF) [5], which can learn an effective subspace for classification and clustering. NMF decomposes an original non-negative matrix into two non-negative matrices, such that their product approximates to the original data matrix. The non-negative property is consistent with the humans perception, which is more meaningful in image representation. Due to the satisfactory performance of NMF, some extensions [6,7,8,9,10,11,12,13,14,15,16,17,18,19] were proposed and utilized to improve the clustering effect.

Traditional NMF is an unsupervised method and cannot be designed for clustering specially. To achieve the better clustering effect, some constraints (i.e., label propagation, manifold learning, pairwise constraint, etc.) were considered to constrain the subspace, which can learn a more effective parts-based representation. When the original data are heavily corrupted, NMF fails to achieve clustering. This is because its loss function is more sensitive to outliers and noise. Therefore, some researchers [6,7,8,9,10,11,12] proposed some other loss functions to try better matrix factorization. Gao et al. [9] presented a capped norm as the loss function and an outlier threshold to reduce outliers. However, there is no theory to adjust the threshold. Recently, Guan et al. [12] proposed the Truncated Cauchy loss (CauchyNMF) as the loss function and the three-sigma-rule to filter outliers. Although CauchyNMF learns a better subspace from the original data space contaminated by outliers and noise than other NMF methods, it leads to an unsatisfactory subspace when the outliers cannot follow the Gaussian distribution.

After dimensionality reduction by non-negative matrix factorization, the parts-based representation composed of real numbers will take much more time in clustering. Recently, data-dependent hashing methods [20,21,22,23,24,25,26,27,28] were put forward to learn the latent features of training data and achieved effective binary codes from different hash functions. It is obvious that a subspace composed of binary codes (\(-1\) and 1 or 0 and 1) can reduce the clustering time. However, the traditional NMF cannot learn a parts-based representation composed of binary codes.

In this paper, based on data-dependent hashing methods, non-negative matrix factorization, and manifold learning, a novel dimensionality reduction method is presented to learn a subspace composed of binary codes from the original data space. Our achievements are as follows:

  • A robust non-negative matrix factorization framework was proposed to remove outliers in the subspace. Moreover, the learned subspace composed of binary codes obeys the geometrical assumption of the original data.

  • Our problem can be formulated as a mixed integer optimization problem. We transform it into several subproblems and elegantly solve these subproblems.

  • Extensive experiments prove that our method can learn a subspace composed of binary codes from the dataset corrupted by Salt and Pepper noise and Contiguous Occlusion. Moreover, the clustering performance from the subspace can demonstrate that our method can achieve the better clustering effect than other dimensionality reduction methods.

Related works

Non-negative matrix factorization and its extensions

Supposed that any image can be represented by a vector \(x_i \in R^m\) and the matrix \(V=[x_1,\ldots ,x_n]\) denotes an original image space composed of n images. NMF can be utilized to discover two low-dimensional matrices \(W \in R^{m \times r}\) and \(H \in R^{r \times n}\), such that their product can best approximate to V, where r is a factorization rank and \(r<<\min \{m,n\}\). Generally, NMF can be mathematically formulated as follows:

$$\begin{aligned}&\min _{W,H} \quad \mathrm{{Loss}} (V,WH) \nonumber \\&\mathrm{{s.t.}} \quad W \ge 0, H \ge 0, \end{aligned}$$
(1)

where the function Loss is to measure the error between V and WH. The usual loss function can be \(L_1\) norm, \(L_{2,1}\) norm, or the Frobenius norm. Guan et al. [12] put forward a Truncated Cauchy loss to reduce outliers (CauchyNMF), which can be written by the following form:

$$\begin{aligned} \min _{W \ge 0,H \ge 0} F(W,H)=\sum _{i=1}^m\sum _{j=1}^n g\left( \frac{(V-WH)_{ij}}{\gamma }\right) , \end{aligned}$$
(2)

where \(g(x)= {\left\{ \begin{array}{ll} \ln (1+x), &{}0 \le x \le \sigma \\ \ln (1+\sigma ) , &{} x>\sigma . \end{array}\right. }\) The scale parameter \(\sigma \) can be computed by three-sigma-rule, and the truncation parameter \(\gamma \) can be achieved by the Nagy algorithm [12]. Most of NMF variants utilize various loss function to handle outliers, but these approaches cannot remove outliers in the subspace. To address this problem, a novel robust NMF framework was put forward as follows:

$$\begin{aligned} \begin{aligned}&\min _{W,H,E} \quad \mathrm{{Loss}} (M,WH,E)+\lambda \Omega (E,W,H)\\&\mathrm{{s.t.}} \quad W \ge 0, H \ge 0, \end{aligned} \end{aligned}$$
(3)

where M is the original data matrix contaminated by outliers, E is an error matrix, \(\lambda \) is a hyper-parameter, and \(\Omega \) is the constraint term. Based on problem (3), Zhang et al. [11] proposed the following robust NMF problem:

$$\begin{aligned} \begin{aligned}&\min _{W,H,E} \parallel M-WH-E\parallel _F^2+\lambda \parallel E \parallel _M\\&\mathrm{{s.t.}} \quad W \ge 0, H \ge 0, \end{aligned} \end{aligned}$$
(4)

where \(\parallel E \parallel _M=\sum _{ij}|e_{ij}|\).

Data-dependent hashing methods

Assumed that an image sample is expressed by the vector \(v \in R^m\) and the original data space is showed by the matrix \(V=[v_i,\cdots ,v_n] \in R^{m \times n}\) . Data-dependent hashing methods expect to find a binary code matrix \(B \in \{-1,1\}^{L\times n}\), which can maintain the semantic similarities of the data space. Usually, each column of B is L-bit codes for each v, where \(L<<m\).

To make full use of the label information of the original data, Shen et al. [25] put forwarded a supervised discrete hashing framework, which can generate binary codes with satisfactory linear classification. Supposed that an original data matrix \(V=[v_1,\ldots ,v_n] \in R^{m \times n}\), a label matrix \(Y \in \{0,1\}^{c\times n}\), a binary code matrix \(B \in \{0,1\}^{L\times n}\), \(W \in R^{L \times c}\), and \(P\in R^{m \times L}\). SDH are able to sum up by:

$$\begin{aligned} \begin{aligned} \min _{W,B,P} \quad&\parallel Y-W^TB\parallel _F^2 +\lambda \parallel W \parallel _F^2\\&+\mu \parallel B-P^T \phi (V) \parallel _F^2 \\ \mathrm {s.t.} \quad&B \in \{0,1\}^{L\times n}, \end{aligned} \end{aligned}$$
(5)

where \(\phi (\cdot )\) is the RBF kernel mapping, \(\mu \) and \(\lambda \) are penalty parameters. For the purpose of solving problem (5), we can optimize the following three subproblems:

$$\begin{aligned} \min _{W} \quad \parallel Y-W^TB\parallel _F^2 +\lambda \parallel W \parallel _F^2 \end{aligned}$$
(6)

and

$$\begin{aligned} \begin{aligned} \min _{W,B,P} \quad&\parallel Y-W^TB\parallel _F^2+\mu \parallel B-P^T \phi (V) \parallel _F^2 \\ \mathrm {s.t.} \quad&B \in \{0,1\}^{L\times n} \end{aligned} \end{aligned}$$
(7)

and

$$\begin{aligned} \parallel B-P^T \phi (V) \parallel _F^2, \end{aligned}$$
(8)

until the stop condition is satisfied. Thus, we are able to obtain the local optimal solution of problem (5).

In response to this problem (6), we have:

$$\begin{aligned} W=(BB^T+\lambda )^{-1}BY^T. \end{aligned}$$
(9)

In response to this problem (7), we make the following assumptions:

  • \(z^T\) is the lth row of B and \(B^{\prime }\) is the matrix of B not including z.

  • \(q^T\) is the lth row of \(WY+\mu P^T \phi (V)\) and \(Q^{\prime }\) is the matrix of Q not including q.

  • \(v^T\) is the lth row of W and \(W^{\prime }\) is the matrix of W not including v.

We can safely come to the conclusion that:

$$\begin{aligned} z=\mathrm{{sign}}(q-{B^{\prime }}^TW^{\prime }v). \end{aligned}$$
(10)

With regard to problem (8), the solution is:

$$\begin{aligned} P=(\phi (V){\phi (V)}^T)^{-1}\phi (V)B^T. \end{aligned}$$
(11)

Consequently, it is easy to search the local optimal solution of the problem (5) using (9), (10), and (11).

Problem formulation

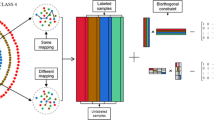
When the original data are destroyed by outliers and noise, existing NMF methods have the following shortcomings: (1) They are unable to learn an effective and powerful subspace from the original data space. (2) The parts-based representation is unable to retain the geometrical structure information of the original data. (3) These NMF methods are unable to learn a subspace with binary codes.

For problem (4), Zhang et al. [11] assumed that the outliers of the error matrix E are very sparse. Yet, the abnormal position of the original data is ignored. Supposed that we become aware of some outlier locations. For an image space \(M\in R^{m\times n}\), a weighted graph S marks the location of outliers by the following equation:

$$\begin{aligned} S_{ij}= {\left\{ \begin{array}{ll} 0, &{}\text {if}\, M_{ij}\,\text {is an outlier}, \\ 1, &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$
(12)

Hence, we rewrite the constraint on E as follows:

$$\begin{aligned} \parallel E\otimes S \parallel _F^2. \end{aligned}$$
(13)

To obtain the geometric information in subspace, manifold regularization can be used to establish the relation between the original data space and the subspace. Therefore, a common used method called manifold learning [29] is as follows:

$$\begin{aligned} \mathrm{tr}(H(D-U)H^T), \end{aligned}$$
(14)

where tr is the trace of a matrix, \(U_{jl}=e^{-\frac{\parallel x_j-x_l\parallel ^2}{\sigma }}\) and \(D_{ii}=\sum _j W_{ij}\).

In summary, combining (13), (14), and (4) results in our robust semi-supervised non-negative matrix factorization for binary subspace learning (RSNMF). Given a non-negative data matrix \(V \in R^{m \times n}\) and a factorization r, one hopes to achieve a code matrix \(B \in \{-1,+1\}^{r\times n}\) from V. Our proposed robust semi-supervised non-negative matrix factorization (RSNMF) can be utilized to learn binary codes for clustering. There are three properties as follows:

  • The learned subspace can remove outliers and noise similar to (4).

  • The subspace composed of binary codes can be learned from the data space similar to (5). (5) is a supervised problem; therefore, we delete the first two terms of (5) to be an unsupervised problem.

  • The low-dimensional space composed of binary codes should remain similarity or dissimilarity of the original data space similar to (14).

Combining (4), (5), and (14), our problem can be formulated as follows:

$$\begin{aligned} \begin{aligned}&\min _{W,H,E,B,P} F(W,H,E,B,P) \\&\quad =\,\parallel M-WH-E\parallel _F^2+\lambda \parallel E \otimes S \parallel _F^2 \\&\qquad +\gamma \mathrm{{tr}}(H(D-U)H^T) \\&\qquad +\gamma {\text {tr}}(B (D-U) B^{T})+\alpha \left\| B-PH\right\| _{F}^{2}\\&\mathrm{{s.t.}} \quad W \ge 0, H \ge 0, B \in \{-1,1\}. \end{aligned} \end{aligned}$$
(15)

where \(\lambda \), \(\gamma \), and \(\alpha \) are hyper-parameters.

Optimization scheme

Problem (15) is a non-convex optimization problem. Thus, it is unable to search the global optimal solution. A generic framework for solving problem (15) is the “block-coordinate-descent” method (BCD) [30], in which one block variables are solved in order under relevant constraints and the remaining variables remain fixed. Thus, problem (15) can be converted into several convex problems and solve them in turn until convergence. For (15), we have five block variables W, H, B, P, and E. Thus, BCD is able to optimize the five matrices in turn. Supposed that the kth solution of problem (15) has been realized. The \(k+1\)th solution can be searched by:

$$\begin{aligned} E^{k+1}&={\arg \min }_E \parallel M-W^kH^k-E\parallel _F^2\nonumber \\&\quad +\lambda \parallel E \otimes S \parallel _F^2 \end{aligned}$$
(16)

and

$$\begin{aligned} W^{k+1}&={\arg \min }_W \parallel M-WH^k-E^{k+1}\parallel _F^2\nonumber \\&\quad \mathrm{{s.t.}} \quad W \ge 0 \end{aligned}$$
(17)

and

$$\begin{aligned} \begin{aligned}&H^{k+1}\\&\quad ={\arg \min }_H \parallel M-W^{k+1}H-E^{k+1}\parallel _F^2\\&\qquad +\alpha \left\| B-PH\right\| _{F}^{2}+\gamma \mathrm{{tr}}(H(D-U)H^T)\\&\mathrm{{s.t.}} \quad H \ge 0, \end{aligned} \end{aligned}$$
(18)

and

$$\begin{aligned} P^{k+1} ={\arg \min }_P \parallel B^{k+1}-PH^{k+1}\parallel _{F}^{2} \end{aligned}$$
(19)

and

$$\begin{aligned} \begin{aligned}&B^{k+1}\\&\quad ={\arg \min }_B (\alpha \parallel B^{k+1}-P^{k+1}H^{k+1} \parallel _{F}^{2} \\&\qquad +\gamma \mathrm{{tr}}(B (D-U) B^{T})) \\&\mathrm{{s.t.}} \quad B \in \{-1,1\}^{r\times n}. \end{aligned} \end{aligned}$$
(20)

It is easy to get the solution of problems (4) and (4) as follows:

$$\begin{aligned}&e_{ij} \leftarrow \frac{m_{ij}-(WH)_{ij}}{1+\lambda s_{ij}}. \end{aligned}$$
(21)
$$\begin{aligned}&w_{il} \leftarrow w_{il} \frac{(M{H}^T)_{il}-{(EH^T)}_{il}}{(WHH^T)_{il}}. \end{aligned}$$
(22)

For (18), we can utilize Nesterov’s optimal method [31] to solve it. To save space, we do not introduce this algorithm. For problem (19), we have the optimal solution:

$$\begin{aligned} \begin{aligned} P=BH^T{(HH^T)}^{-1} \end{aligned} \end{aligned}$$
(23)

or

$$\begin{aligned} \begin{aligned} P^T={(HH^T)}^{-1}HB^T, P=(P^T)^T. \end{aligned} \end{aligned}$$
(24)

Using a function RRC in [25], Eq. (24) can be realized . Therefore, the solution of (19) can be realized by:

$$\begin{aligned} \begin{aligned} P&=\mathrm{RRC}(H^T, B^T, 0) \\ P&=P^T. \end{aligned} \end{aligned}$$
(25)

For problem (20), using the discrete cyclic coordinated descent method, we can achieve its local optimal solution. First, problem (20) can be converted into the following form:

$$\begin{aligned} F(B)=(\alpha \left\| B-PH\right\| _{F}^{2}+\beta \mathrm{{tr}}(BKCB^T)), \end{aligned}$$
(26)

where \(K=D-U\) and \(C \in R^{n \times n}\) is an identity matrix. Second, some assumptions are made as follows:

  • z is the kth column of B and \(B^{\prime }\) is the matrix of B excluding z. Thus, \(B=[z \quad B^{\prime }]\).

  • c is the kth column of C and \(C^{\prime }\) is the matrix of C excluding c. Thus, \(C=[c \quad C^{\prime }]\).

  • \(k^T\) is the kth row of K and \(K^{\prime }\) is the matrix of K excluding k. Thus, \(K= \begin{bmatrix} k^T \\ K^{\prime }\end{bmatrix}\)

  • \(Q=PH\). q is the kth column of Q and \(Q^{\prime }\) is the matrix of B excluding q. Thus, \(Q=[q \quad Q^{\prime }]\).

Thirdly, B can be learned column by column. The first term of problem (26) is rewritten as follows:

$$\begin{aligned} \begin{aligned}&\parallel B-PH\parallel _F^2 \\&\quad =\parallel z-q\parallel _F^2+\parallel B^{\prime }-Q^{\prime }\parallel _F^2 \\&\quad =\mathrm{{tr}}((z-q)^T(z-q))+ \mathrm{{const}}\\&\quad =\mathrm{{tr}}(z^Tz-z^Tq-q^Tz+q^Tq)+\mathrm{{const}}\\&\quad =-2\mathrm{{tr}}(q^Tz)+\mathrm{{const}}. \end{aligned} \end{aligned}$$
(27)

Similar to the second term of problem (26), we are able to conclude that:

$$\begin{aligned} \begin{aligned}&\mathrm{{tr}}(BKCB^T)\\&\quad =\mathrm{{tr}}((zk^T+B^{\prime }K^{\prime })(cz^T+C^{\prime }{B^{\prime }}^T))\\&\quad =\mathrm{{tr}}(zk^Tcz^T+zk^TC^{\prime }{B^{\prime }}^T+B^{\prime }K^{\prime }cz^T\\&\qquad +B^{\prime }K^{\prime }C^{\prime }{B^{\prime }}^T) \\&\quad =\mathrm{{tr}}(zk^TC^{\prime }{B^{\prime }}^T)+\mathrm{{tr}}(B^{\prime }K^{\prime }cz^T)+\mathrm{{const}} \\&\quad =2\mathrm{{tr}}(k^TC^{\prime }{B^{\prime }}^Tz)+\mathrm{{const}}.\\ \end{aligned} \end{aligned}$$
(28)

Therefore, problem (20) can be rewritten by:

$$\begin{aligned} \begin{aligned}&\min _{z} \quad \beta \mathrm{{tr}}(k^TC^{\prime }{B^{\prime }}^Tz)-\alpha \mathrm{{tr}}(q^Tz) \\&\quad \mathrm {s.t.} \quad z\in \{-1,1\}^r. \end{aligned} \end{aligned}$$
(29)

This problem brings about the following optimal solution:

$$\begin{aligned} z= \mathrm{{sign}}(\alpha q- \beta B^{\prime }{C^{\prime }}^Tk). \end{aligned}$$
(30)

Obviously, each z can be calculated from the pre-learned \(B^{\prime }\) in advance. Hence, we can implement B before each z is updated. In [25], it is recommended (30) be used to learn the binary code matrix B in t times, where \(t=5\).

Fig. 1
figure 1

Sample images from ORL and YALE

Full size image
figure a

Experimental results

Experiment setup

We compare our proposed method (RSNMF) with NMF [5], RNMF_L1 [9], PCA [4], and CauchyNMF [12] on the clustering performances of two datasets (i.e., ORL and YALE) contaminated by Salt and Pepper noise and Contiguous Occlusion.

Fig. 2
figure 2

Clustering ACs and NMIs on ORL and YALE when the corrupted percentage varies from 0.05 to 0.8 with the step size 0.05

Full size image
Fig. 3
figure 3

Clustering ACs and NMIs on ORL and YALE when the corrupted block size varies from 1 to 24 with the step size 2

Full size image

ORL contains a set of the frontal face images, and these images were established from 1992 to 1994 by Cambridge University. There are 40 various persons, and each person includes 10 images. Each image were taken at different facial expressions, times, and so on. The format of each image is PGM with the size of \(92\times 122\) pixels. We scale down each image to \(32\times 32\) pixels. YALE was constructed by the Center for Computational Vision and Control of Yale University. There are 165 images of 15 persons, and each person contains 11 pictures. Each image was taken by different facial expressions or configurations with the size of \(100 \times 100\) pixels. Some example images from ORL and YALE are presented in Fig. 1.

To verify the clustering ability on the corrupted data, we propose two corruptions including Salt and Pepper noise and Contiguous Occlusion. Salt and Pepper noise is utilized to change a portion of pixel values to be 0–255. The corrupted percentage of pixels is from 0.05 to 0.8 with the step size 0.05. Contiguous Occlusion randomly corrupts a block of each image and the pixels of the block is filled with 255. The corrupted block size is proposed to be 1 to 24 with the step size 2. Supposed that \(r=32\), \(alpha=0.1\), \(\gamma =1e^{-5}\), \(\lambda =100\), and \(iter=200\). We propose Accuracy (AC) and Normalized Mutual Information (NMI) [32] to validate the clustering effect of each algorithm.

Salt and Pepper noise

Figure 2 presents the clustering performance on ORL and YALE when the two datasets are contaminated by Salt and Pepper noise. From these figures, we observe that:

  • For ORL, the best AC and NMI obtained by CauchyNMF are 0.65 and 0.8, respectively. For YALE, the best AC and NMI achieved by CauchyNMF are 0.48 and 0.52, respectively.

  • RSNMF and CauchyNMF have the better ACs and NMIs than other methods. CauchyNMF performs better than RSNMF in the beginning; however, it becomes worse when the corrupted percentage varies.

  • For the smaller corrupted percentage, all methods can not only learn a satisfactory subspace, but also achieve excellent clustering results. When ORL is heavily corrupted (i.e., the corrupted percentage greater than 0.4), only RSNMF remains the satisfactory clustering results.

Contiguous occlusion

Figure 3 presents the clustering performance on ORL and YALE when the two datasets are contaminated by Contiguous Occlusion. From these figures, there are some interesting points as follows:

  • NMF, PCA, and RNMF_L1 achieve satisfactory clustering results when the block size is very small.

  • CauchyNMF achieves the best AC and NMI with the smaller block size (i.e., the block size less than 6). As the block size is greater than 10, CauchyNMF performs worse rapidly.

  • Although RSNMF performs not better than CauchyNMF in the beginning, it remains stable clustering results as the block size increases.

Conclusion

This paper presented a robust semi-supervised non-negative matrix factorization for binary subspace learning (RSNMF) to handle Salt and Pepper noise and Contiguous Occlusion. The clustering performances demonstrate that our method achieves the following advantages. First, RSNMF can learn a more effective and discriminative parts-based representation composed of binary codes from ORL and YALE corrupted by Salt and Pepper noise and Contiguous Occlusion. Second, RSNMF is more robust to outliers than the existing dimensionality reduction methods.