Introduction

The unit cost of each product is a critical performance measure for a factory [12]. Compared with other performance measures such as yield and productivity, the unit cost is special for the following reasons:

  1. 1.

    Since the profit is derived by subtracting the price by the unit cost, a lower unit cost immediately increases the profit.

  2. 2.

    The unit cost is both a direct performance measure and an indirect performance measure. Before production, a reduction in the prices of raw materials is directly reflected in the unit cost of the finished goods. After production, a higher yield results in more output that drives down the unit cost further.

In addition, estimating the unit cost of each product accurately is a prerequisite to determining the profitability of a manufacturer. However, owing to the prevalent “cost down” philosophy, many manufacturers incorrectly expect that the unit cost of a product can be reduced in a linear way. This is a misunderstanding because if a linear cost-down works out, the unit cost will eventually become negative. For this reason, fitting the reduction in the unit cost of a product with a learning process has become a common practice [28].

The motivation for this study is explained as follows. A problem of the existing methods is that they often deal with the logarithmic or log-sigmoid value, rather than the original value, of the unit cost, as shown in Table 1. The reason for such a treatment is to simplify the required computation or to utilize an existing training algorithm. However, in this way, the estimating accuracy or precision with respect to the original value of the unit cost has not truly been optimized. To resolve this problem, a new fuzzy collaborative intelligence (FCI) approach that can deal with the original value of the unit cost is proposed in this study. This is a homogeneous FCI method because all models are built by solving the same, i.e., mathematical programming (MP), problems.

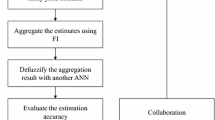
Table 1 Types of the unit-cost value in existing unit cost estimation methods
Full size table

In the proposed new FCI approach, the logarithmic function is approximated with a polynomial function. Then, the two nonlinear programming (NLP) models formulated by Chen [10] are converted into equivalent polynomial programming (PP) models. Subsequently, each expert applies either PP model to estimate the unit cost of a product. Finally, the fuzzy unit cost estimates from the experts are aggregated using the fuzzy intersection (FI)-back propagation network (BPN) approach proposed by Chen and Lin [9]. The effectiveness of the proposed methodology is validated with a real case.

The differences between the proposed methodology and some existing methods are summarized in Table 2, showing the originality of the proposed methodology.

Table 2 The differences between the proposed methodology and some existing methods
Full size table

The contribution of this study is the designing of the PP formulations that can deal with the original value of the unit cost in modeling the uncertain unit cost learning process, which is the first attempt in this field and has great potential of improving the precision and accuracy of estimating the unit cost.

The remainder of this paper is organized as follows. Section 2 is dedicated to the literature review. In Sect. 3, the models and steps of the proposed new FCI approach are detailed. In Sect. 3, a real dynamic random access memory (DRAM) case is adopted to validate the effectiveness of the new FCI approach. Two existing FCI methods are also applied to the real case for a comparison. Finally, in Sect. 4, some conclusions are drawn, from which several directions for future investigation are also given.

Previous work

Some of the related literature on the unit cost estimation is reviewed as follows. Estimating the unit cost of a product is not an easy task in many industries. Cohen et al. [15] analyzed the data of cancellation costs, holding costs, and delay costs of suppliers in a semiconductor equipment supply chain. The collected data indicated that a supplier perceived the cancellation costs to be about two times higher than the delay costs, and the holding costs to be about three times higher than the delay costs. Such perceptions may be misleading and undermine the effectiveness of a unit cost estimation mechanism. The unit cost is determined by yield that is subject to significant uncertainty caused by human intervention. To address this, several studies estimated the unit cost of a product with a fuzzy value. The maximum (minimum) of the fuzzy value indicates the highest (lowest) possible value of the unit cost, which happens when the yield is at the lowest (highest) level [7]. For example, in Wu et al. [30], the quality of raw materials from suppliers was unstable and was modeled with a trapezoidal fuzzy number (TrFN). As a result, the unit cost became a TrFN as well. Based on that, a fuzzy multi-objective programming model was established for supplier selection and risk modeling. Chen [10] modeled the unit cost of a DRAM product with a triangular fuzzy number (TFN). Lee et al. [20] observed that the cost per bit of DRAM has been decreasing at a rapid rate with advances in DRAM processing technologies that scale more DRAM cells into the same die area. Many studies on production planning considered this fact by incorporating in fuzzy unit cost estimates. For example, Vijayan and Kumaran [29] minimized the total inventory costs when the unit costs were estimated with fuzzy numbers. In Zhao et al. [31], the unit cost of each product was modeled as a fuzzy number, based on which the pricing decisions for substitutable products could be made. In addition to modeling uncertain learning processes, fuzzy logic has been extensively applied to designing controllers in a noisy environment [3, 4, 6, 23, 26].

In the past, the application of fuzzy logic to the unit cost estimation did not receive much attention in the manufacturing sector [21]. However, the great potential has been mentioned by studies like Chang et al. [8]. Recently, some studies proposed fuzzy methods, especially FCI methods, to estimate the unit cost of a product. The FCI methods gather several experts that apply fuzzy methods to estimate the unit cost of a product [24]. Then, the fuzzy unit cost estimates from the experts are aggregated [25]. For example, Chen [10] proposed an FCI method in which experts fitted fuzzy linear regression (FLR) equations to estimate the effective cost per die of a semiconductor product. Then, the fuzzy unit cost estimates from the experts were aggregated using the FI-BPN approach. Hsiao et al. [18] applied fuzzy neural network (FNN) and genetic algorithm jointly to estimating the hookup construction cost of a semiconductor fabrication plant. Chen [11] proposed another FCI method in which experts configured FNNs to estimate the unit cost and then a radial basis function (RBF) network was used to aggregate the fuzzy unit cost estimates. Recently, the FCI method proposed by Chen and Chiu [13] used software agents to quicken the collaboration process.

In sum, the existing FCI methods can be divided into expert-based and agent-based types depending on whether real experts or software agents are involved. The advantages and disadvantages of the two types of FCI methods are summarized in Table 3. In addition, an FCI method can be homogeneous if the experts apply the same types of fuzzy methods, or heterogeneous if experts apply different types of fuzzy methods. As a consequence, theoretically, the existing methods can be classified into four categories, as shown in Fig. 1. Most of the existing FCI methods, e.g., Chen [10], Chen [11], and Chen and Chiu [13], fall into the Type I category. The proposed methodology also belongs to the Type I category.

Table 3 Advantages and disadvantages of two types of FCI methods
Full size table
Fig. 1
figure 1

Categories of existing FCI methods

Full size image

The new FCI approach

A fuzzy unit cost learning model

Without loss of generality, all fuzzy variables or parameters in the new FCI approach are given in TFNs that are defined as follows.

Definition 1

(TFN). A TFN \( \tilde{A} = (A_{1} ,\;A_{2} ,\;A_{3} ) \) is a fuzzy number with the following membership function:

$$ \mu_{{\tilde{A}}} (x) = \hbox{min} \left( {\hbox{max} \left( {\frac{{x - A_{1} }}{{A_{2} - A_{1} }},\;0} \right),\;\hbox{max} \left( {\frac{{x - A_{3} }}{{A_{2} - A_{3} }},0} \right)} \right). $$
(1)

A fuzzy unit cost learning model can be described as [13]:

$$ \tilde{C}_{t} = \tilde{C}_{0} {\text{e}}^{{\frac{{\tilde{b}}}{t}}} , $$
(2)

where \( \tilde{C}_{t} = (C_{t1} ,\;C_{t2} ,\;C_{t3} ) \) is the fuzzy unit cost estimate within time period t; \( 0\le \tilde{C}_{t} \); t = 1 ~ T. \( \tilde{C}_{0} = (C_{01} ,\;C_{02} ,\;C_{03} ) \) is the asymptotic (or final) unit cost; \( 0\le \tilde{C}_{ 0} \). \( \tilde{b} = (b_{1} ,\;b_{2} ,\;b_{3} ) \) is the learning constant; \( \tilde{b} \geq 0.\) According to the arithmetic on TFNs [32],

$$ C_{t1} \cong C_{01} {\text{e}}^{{\frac{{b_{1} }}{t}}} , $$
(3)
$$ C_{t2} \cong C_{02} {\text{e}}^{{\frac{{b_{2} }}{t}}} , $$
(4)
$$ C_{t3} \cong C_{03} {\text{e}}^{{\frac{{b_{3} }}{t}}} , $$
(5)

Converting the parameters on both sides of (3)–(5) to their logarithmic values gives:

$$ \ln C_{t1} \cong \ln C_{01} + b_{1} /t, $$
(6)
$$ \ln C_{t2} \cong \ln C_{02} + b_{2} /t, $$
(7)
$$ \ln C_{t3} \cong \ln C_{03} + b_{3} /t, $$
(8)

Chen’s FCI method

Chen [10] proposed an FCI method for DRAM unit cost estimation. In the FCI method, each expert formulates either of the following NLP models to estimate the unit cost of a DRAM product:

(Model NLPI)

$$ {\text{Min}}\;\;Z_{\text{NLPI}} = \sum\limits_{t = 1}^{T} {(\ln C_{t3} - \ln C_{t1} )^{o(k)} } , $$
(9)

subject to

$$ \ln C_{t} \ge \ln C_{t1} + s(k)(\ln C_{t2} - \ln C_{t1} ), $$
(10)
$$ \ln C_{t} \le \ln C_{t3} + s(k)(\ln C_{t2} - \ln C_{t3} ), $$
(11)
$$ \ln C_{t1} = \ln C_{01} + b_{1} /t, $$
(12)
$$ \ln C_{t2} = \ln C_{02} + b_{2} /t, $$
(13)
$$ \ln C_{t3} = \ln C_{03} + b_{3} /t, $$
(14)
$$ \ln C_{01} \le \ln C_{02} \le \ln C_{03} , $$
(15)
$$ 0 \le b_{1} \le b_{2} \le b_{3} , $$
(16)
$$ t = { 1 }\sim T $$

The objective function minimizes the higher-order sum of ranges of the unit cost estimates. Constraints (10) and (11) request that the membership of the actual value in the fuzzy unit cost estimate to be greater than \( s(k) \). Constraints (15) and (16) define the sequence of the three corners of the corresponding TFN.

(Model NLPII)

$$ {\text{Max}}\;\;Z_{\text{NLPII}} = \sqrt[{m(k)}]{{\sum\limits_{t = 1}^{T} {s_{t}^{m(k)} } }}, $$
(17)

subject to:

$$ \sum\limits_{t = 1}^{T} {(\ln C_{t3} - \ln C_{t1} )^{o(k)} \le Td(k)^{o(k)} } , $$
(18)
$$ \ln C_{t} \ge \ln C_{t1} + s_{t} (\ln C_{t2} - \ln C_{t1} ), $$
(19)
$$ \ln C_{t} \le \ln C_{t3} + s_{t} (\ln C_{t2} - \ln C_{t3} ), $$
(20)
$$ \ln C_{t1} = \ln C_{01} + b_{1} /t, $$
(21)
$$ \ln C_{t2} = \ln C_{02} + b_{2} /t, $$
(22)
$$ \ln C_{t3} = \ln C_{03} + b_{3} /t, $$
(23)
$$ \ln C_{01} \le \ln C_{02} \le \ln C_{03} , $$
(24)
$$ 0 \le b_{1} \le b_{2} \le b_{3} , $$
(25)
$$ 0 \le s_{t} \le 1, $$
(26)
$$ t = { 1 }\sim T, $$

where \( o(k) \), \( s(k) \), \( m(k) \), and \( d(k) \) are the optimization parameters specified by expert k; k = 1 ~ K. \( o(k) \), \( m(k) \in Z^{ + } \); \( s(k) \in [0,\;1] \); \( d(k) \ge 0 \). In Model NLPI, The objective function maximizes the generalized mean of the satisfaction levels that are explained below. Constraints (19) and (20) request that the membership of the actual value in the fuzzy unit cost estimate to be greater than \( s_{t} \). Constraints (24) and (25) define the sequences of the three corners of the TFNs.

Definition 2

(The satisfaction level). The satisfaction level (s) is the minimal membership in which an actual value (\( A_{i} \)) belongs to the corresponding fuzzy estimate (\( \tilde{E}_{i} \)):

$$ s = \mathop {\hbox{min} }\limits_{i} \mu_{{\tilde{E}_{i} }} (A_{i} ) $$
(27)

The objective function (17) can be replaced by

$$ {\text{Max}}\;\;Z_{\text{NLPII}}^{'} = \sum\limits_{t = 1}^{T} {s_{t}^{m(k)} } $$
(28)

In Chen’s method, the logarithmic values of parameters were derived instead of their original values to simplify the computation. As a result, the optimization results apply only to the logarithmic values, and not to the original values, of the unit cost.

The new FCI approach

In the new FCI approach, first, a polynomial function is used to approximate the logarithmic function. However, the problem is that it is difficult to approximate the logarithmic function within a wide range with a limited-order polynomial function to a sufficient degree of precision. To resolve this difficulty, the range of the unit cost is determined. For example, if 0.5 ≤ x ≤ 2.5, then

$$ \ln x \cong - 1.9404 + 3.3364x - 1.9411x^{2} + 0.6276x^{3} - 0.0810x^{4} $$
(29)

The absolute error of such an approximation is less than 0.01, as shown in Fig. 2:

Fig. 2
figure 2

Polynomial approximation of the logarithmic function

Full size image
$$ |\ln x - ( - 1.9404 + 3.3364x - 1.9411x^{2} + 0.6276x^{3} - 0.0810x^{4} )| \le 0.01; \, 0. 5\;x\; 2. 5 $$
(30)

The approximation formulae for some other ranges are provided in Table 4.

Table 4 Approximation formulae for some other ranges
Full size table

Substituting (30) into (12) gives:

$$ \begin{aligned} & 3.3364C_{t1} - 1.9411C_{t1}^{2} + 0.6276C_{t1}^{3} - 0.0810C_{t1}^{4} \\ &\quad= 3.3364C_{01} - 1.9411C_{01}^{2} + 0.6276C_{01}^{3} - 0.0810C_{01}^{4} + b_{1} /t. \\ \end{aligned} $$
(31)

Similarly, (13) and (14) can also be approximated as:

$$ \begin{aligned} & 3.3364C_{t2} - 1.9411C_{t2}^{2} + 0.6276C_{t2}^{3} - 0.0810C_{t2}^{4} \\ &\quad= 3.3364C_{02} - 1.9411C_{02}^{2} + 0.6276C_{02}^{3} - 0.0810C_{02}^{4} + b_{2} /t, \\ \end{aligned} $$
(32)
$$ \begin{aligned} & 3.3364C_{t3} - 1.9411C_{t3}^{2} + 0.6276C_{t3}^{3} - 0.0810C_{t3}^{4} \\ &\quad= 3.3364C_{03} - 1.9411C_{03}^{2} + 0.6276C_{03}^{3} - 0.0810C_{03}^{4} + b_{3} /t. \\ \end{aligned} $$
(33)

As a result, the following PP models are built to replace the two NLP models:

(Model PPI)

$$ {\text{Min}}\;\;Z_{\text{PPI}} = \sum\limits_{t = 1}^{T} {(C_{t3} - C_{t1} )^{o(k)} } $$
(34)

subject to:

$$ C_{t} \ge C_{t1} + s(k)(C_{t2} - C_{t1} ), $$
(35)
$$ C_{t} \le C_{t3} + s(k)(C_{t2} - C_{t3} ), $$
(36)
$$ \begin{aligned} & 3.3364C_{t1} - 1.9411C_{t1}^{2} + 0.6276C_{t1}^{3} - 0.0810C_{t1}^{4} \\ &\quad= 3.3364C_{01} - 1.9411C_{01}^{2} + 0.6276C_{01}^{3} - 0.0810C_{01}^{4} + b_{1} /t, \\ \end{aligned} $$
(37)
$$ \begin{aligned} & 3.3364C_{t2} - 1.9411C_{t2}^{2} + 0.6276C_{t2}^{3} - 0.0810C_{t2}^{4} \\ &\quad= 3.3364C_{02} - 1.9411C_{02}^{2} + 0.6276C_{02}^{3} - 0.0810C_{02}^{4} + b_{2} /t, \\ \end{aligned} $$
(38)
$$ \begin{aligned} & 3.3364C_{t3} - 1.9411C_{t3}^{2} + 0.6276C_{t3}^{3} - 0.0810C_{t3}^{4} \\ &\quad= 3.3364C_{03} - 1.9411C_{03}^{2} + 0.6276C_{03}^{3} - 0.0810C_{03}^{4} + b_{3} /t, \\ \end{aligned} $$
(39)
$$ C_{01} \le C_{02} \le C_{03} , $$
(40)
$$ 0 \le b_{1} \le b_{2} \le b_{3} , $$
(41)
$$ t = { 1 }\sim T $$

Compared to model NLP I, the objective function remains unchanged. Only the constraints involving logarithmic terms, i.e., (10)–(15), are replaced with polynomial constraints, i.e., (35)–(40).

(Model PPII)

$$ {\text{Max}}\;\;Z_{\text{PPII}} = \sum\limits_{t = 1}^{T} {s_{t}^{m(k)} } $$
(42)

subject to

$$ \sum\limits_{t = 1}^{T} {(C_{t3} - C_{t1} )^{o(k)} \le Td(k)^{o(k)} } , $$
(43)
$$ C_{t} \ge C_{t1} + s_{t} (C_{t2} - C_{t1} ), $$
(44)
$$ C_{t} \le C_{t3} + s_{t} (C_{t2} - C_{t3} ), $$
(45)
$$ \begin{aligned} & 3.3364C_{t1} - 1.9411C_{t1}^{2} + 0.6276C_{t1}^{3} - 0.0810C_{t1}^{4} \\ &\quad = 3.3364C_{01} - 1.9411C_{01}^{2} + 0.6276C_{01}^{3} - 0.0810C_{01}^{4} + b_{1} /t, \\ \end{aligned} $$
(46)
$$ \begin{aligned} & 3.3364C_{t2} - 1.9411C_{t2}^{2} + 0.6276C_{t2}^{3} - 0.0810C_{t2}^{4} \\ &\quad = 3.3364C_{02} - 1.9411C_{02}^{2} + 0.6276C_{02}^{3} - 0.0810C_{02}^{4} + b_{2} /t, \\ \end{aligned} $$
(47)
$$ \begin{aligned} & 3.3364C_{t3} - 1.9411C_{t3}^{2} + 0.6276C_{t3}^{3} - 0.0810C_{t3}^{4} \\ &\quad = 3.3364C_{03} - 1.9411C_{03}^{2} + 0.6276C_{03}^{3} - 0.0810C_{03}^{4} + b_{3} /t, \\ \end{aligned} $$
(48)
$$ C_{01} \le C_{02} \le C_{03} , $$
(49)
$$ 0 \le b_{1} \le b_{2} \le b_{3} , $$
(50)
$$ 0 \le s_{t} \le 1, $$
(51)
$$ t = { 1 }\sim T $$

The objective function is the same with that of model NLP II, while the constraints involving logarithmic terms, i.e., (18)–(24), are replaced with polynomial constraints, i.e., (43)–(49).

Unlike the two NLP models, the PP models are more tractable because the KKT conditions for the PP problems are also polynomials that can be analytically solved using any mathematics or optimization software [1]. For example, the Lagrangian function for the PPI model is:

$$ \begin{aligned} L_{{\varvec{C}_{\varvec{t}} ,\varvec{\lambda}}} &= \sum\limits_{t = 1}^{T} {(C_{t3} - C_{t1} )^{o(k)} } + \sum\limits_{t = 1}^{T} {\left( {\lambda_{1t} (C_{t1} + s(k)(C_{t2} - C_{t1} ) - C_{t} )} \right)} \\ &\quad + \sum\limits_{t = 1}^{T} {\left( {\lambda_{2t} \left( {C_{t} - C_{t3} - s(k)(C_{t2} - C_{t3} )} \right)} \right)} \\ &\quad + \sum\limits_{t = 1}^{T} {(\mu_{1t} (} 3.3364C_{t1} - 1.9411C_{t1}^{2} + 0.6276C_{t1}^{3} - 0.0810C_{t1}^{4} \\ &\quad - 3.3364C_{01} + 1.9411C_{01}^{2} - 0.6276C_{01}^{3} + 0.0810C_{01}^{4} - b_{1} /t)) \\ &\quad + \sum\limits_{t = 1}^{T} {(\mu_{2t} (} 3.3364C_{t2} - 1.9411C_{t2}^{2} + 0.6276C_{t2}^{3} - 0.0810C_{t2}^{4} \\ &\quad - 3.3364C_{02} + 1.9411C_{02}^{2} - 0.6276C_{02}^{3} + 0.0810C_{02}^{4} - b_{2} /t)) \\ &\quad + \sum\limits_{t = 1}^{T} {(\mu_{3t} (} 3.3364C_{t3} - 1.9411C_{t3}^{2} + 0.6276C_{t3}^{3} - 0.0810C_{t3}^{4} \\ &\quad - 3.3364C_{03} + 1.9411C_{03}^{2} - 0.6276C_{03}^{3} + 0.0810C_{03}^{4} - b_{3} /t)) \\ &\quad + \lambda_{3} (C_{02} - C_{03} ) + \lambda_{4} (C_{01} - C_{02} ) + \lambda_{5} (b_{2} - b_{3} ) + \lambda_{6} (b_{1} - b_{2} ). \\ \end{aligned} $$
(52)

The KKT equations for the PPI model can be derived as:

(Equality constraints for PPI)

$$ \begin{aligned} \frac{\partial L}{{\partial C_{01} }} &= \sum\limits_{t = 1}^{T} {(\mu_{1t} (} - 3.3364 + 3.8822C_{01} \\ &\quad- 1.8828C_{01}^{2} + 0.3240C_{01}^{3} )) + \lambda_{4} = 0, \end{aligned} $$
(53)
$$ \begin{aligned} \frac{\partial L}{{\partial C_{02} }} &= \sum\limits_{t = 1}^{T} {(\mu_{2t} (} - 3.3364 + 3.8822C_{02} \\ &\quad - 1.8828C_{02}^{2} + 0.3240C_{02}^{3} )) + \lambda_{3} - \lambda_{4} = 0, \end{aligned} $$
(54)
$$ \begin{aligned} \frac{\partial L}{{\partial C_{03} }} &= \sum\limits_{t = 1}^{T} {(\mu_{3t} (} - 3.3364 + 3.8822C_{03} \\ &\quad- 1.8828C_{03}^{2} + 0.3240C_{03}^{3} )) - \lambda_{3} = 0, \end{aligned} $$
(55)
$$ \frac{\partial L}{{\partial b_{1} }} = \sum\limits_{t = 1}^{T} {(\mu_{1t} (} - 1/t)) + \lambda_{6} = 0, $$
(56)
$$ \frac{\partial L}{{\partial b_{2} }} = \sum\limits_{t = 1}^{T} {(\mu_{2t} (} - 1/t)) + \lambda_{5} - \lambda_{6} = 0, $$
(57)
$$ \frac{\partial L}{{\partial b_{3} }} = \sum\limits_{t = 1}^{T} {(\mu_{3t} (} - 1/t)) - \lambda_{5} = 0, $$
(58)

(Inequality constraints for PPI)

$$ C_{t} \ge C_{t1} + s(k)(C_{t2} - C_{t1} ), $$
(59)
$$ C_{t} \le C_{t3} + s(k)(C_{t2} - C_{t3} ), $$
(60)
$$ C_{01} - C_{02} \le 0, $$
(61)
$$ C_{02} - C_{03} \le 0, $$
(62)
$$ b_{1} - b_{2} \le 0, $$
(63)
$$ b_{2} - b_{3} \le 0, $$
(64)
$$ \lambda_{1t} ,\;\lambda_{2t} ,\;\lambda_{3} \sim \lambda_{6} ,\;\mu_{1t} \sim \mu_{3t} \ge 0, $$
(65)
$$ t = { 1 }\sim T. $$

Obviously, all these equations or constraints are polynomials.

After estimation, the experts’ fuzzy unit cost estimates are fuzzily intersected to determine the narrowest range of the unit cost:

$$ \mu_{{FI(\tilde{C}_{t} (1),\; \ldots ,\;\tilde{C}_{t} (K))}} (x) = \mathop {\hbox{min} }\limits_{k} (\mu_{{\tilde{C}_{t} (k)}} (x)), $$
(66)

where \( \tilde{C}_{t} (k) \) is the fuzzy unit cost estimate by expert k. Then, a BPN is constructed with the following configuration to derive a single representative value from the fuzzy unit cost estimates:

  1. 1.

    Inputs the normalized values of \( C_{t1} (k) \)–\( C_{t3} (k) \) for each k:

$$ N(C_{t1} (k)) = \frac{{C_{t1} (k) - \mathop {\hbox{min} }\limits_{t} C_{t1} (k)}}{{\mathop {\hbox{max} }\limits_{t} C_{t1} (k) - \mathop {\hbox{min} }\limits_{t} C_{t1} (k)}}, $$
(67)
$$ N(C_{t2} (k)) = \frac{{C_{t2} (k) - \mathop {\hbox{min} }\limits_{t} C_{t2} (k)}}{{\mathop {\hbox{max} }\limits_{t} C_{t2} (k) - \mathop {\hbox{min} }\limits_{t} C_{t2} (k)}}, $$
(68)
$$ N(C_{t3} (k)) = \frac{{C_{t3} (k) - \mathop {\hbox{min} }\limits_{t} C_{t3} (k)}}{{\mathop {\hbox{max} }\limits_{t} C_{t3} (k) - \mathop {\hbox{min} }\limits_{t} C_{t3} (k)}}. $$
(69)

As a result, there are 3 K inputs in total.

  1. 2.

    A single hidden layer with 6 K nodes.

  2. 3.

    Output (\( o_{t} \)) the normalized value of the unit cost estimate. To convert it back to the unnormalized value:

$$ U(o_{t} ) = o_{t} \left(\mathop {\hbox{max} }\limits_{t} C_{t} - \mathop {\hbox{min} }\limits_{t} C_{t} \right) + \mathop {\hbox{min} }\limits_{t} C_{t} , $$
(70)

U(ot) is compared with Ct to evaluate the estimating performance.

  1. 4.

    Training algorithm the Gradient-Descent algorithm [22]. Although the Levenberg–Marquardt algorithm is quick and yields a very small error, it tends to overfit, resulting in a poor generalization for the testing data [16].

Application to a real DRAM case

The real DRAM case discussed by Chen [10] was adopted to illustrate the new FCI approach. As mentioned in Chen and Tsai [14], estimating the unit cost is one of the most critical tasks to a DRAM manufacturer. The real case, shown in Fig. 3, contains the average unit costs of the DRAM product during 10 periods.

Fig. 3
figure 3

A real case

Full size image

Two experts collaborated to estimate the unit cost of the DRAM product using the new FCI approach. Their settings of the parameters were


Expert I: PPI (\( o(1) = 2 \), \( s(1) = 0. 2 5 \))


Expert II: PPII (\( o(2) = 2 \), \( m(2) = 2 \), \( d(2) = 0. 5 0 \))

The data of the first five periods were used to build the PP models. Then, the remaining data were used to evaluate the estimating performance. The fitted unit cost learning models were

$$ \tilde{C}_{t} (1) = (0. 9 9 9 0,\; 1. 4 6 0 2,\; 1. 4 6 0 2){\text{e}}^{{\frac{(0. 5 5 4 7,\;0. 5 5 4 7,\;0. 5 5 4 7)}{t}}} $$
(71)

and

$$ \tilde{C}_{t} (2) = ( 1. 0 8 7 9,\; 1. 4 6 0 2,\; 1. 4 6 0 2){\text{e}}^{{\frac{(0. 5 5 4 7,\;0.554 7,\;0.554 7)}{t}}} , $$
(72)

respectively. The fuzzy unit cost estimates generated by (71) and (72) were fuzzily intersected to determine the narrowest range of the unit cost during each period. The results are shown in Fig. 4.

Fig. 4
figure 4

Determining the narrowest range of the unit cost

Full size image

For a comparison, Chen’s FCI method was also applied to the real case. For a fair comparison, the parameter settings by the experts were not varied. The results are shown in Fig. 5. According to the experimental results,

Fig. 5
figure 5

The narrowest range of the unit cost determined using Chen’s FCI method

Full size image
  1. 1.

    The new FCI approach was more precise than Chen’s FCI method because the average range of the fuzzy unit cost estimates generated using the new FCI was 2% narrower than that generated using Chen’s FCI method.

  2. 2.

    In addition, both methods achieved a hit rate of 80% for the testing data.

  3. 3.

    Another distinction between the two methods was the unit cost at the ninth period. The actual value fell near the border of the fuzzy unit cost estimate generated using the new FCI approach, but was considerably outside that generated using Chen’s method, showing the superiority of the new FCI approach over Chen’s FCI method.

Subsequently, a BPN was constructed to derive the representative value of the unit cost from the fuzzy unit cost estimates. MATLAB 2017a was applied to implement the BPN on a PC with an Intel Core i7-7700 3.6-GHz CPU with 8 GB of RAM. The BPN was considered to be converged if the mean squared error (MSE) became less than 10−4. The maximal number of epochs was set to 1000. The estimation results, i.e., the representative values of the unit cost estimates during the periods, are summarized in Fig. 6. Chen’s method was also applied and the results are shown in Fig. 7.

Fig. 6
figure 6

The representative values during various periods

Full size image
Fig. 7
figure 7

The estimating results using Chen’s method

Full size image

The estimating accuracy was measured in terms of the mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean squared error (RMSE). The performances of the two methods in improving the estimating accuracy are compared in Table 5. Obviously, the new FCI approach surpassed Chen’s FCI method in terms of MAE or MAPE. The performances of the two methods with regard to RMSE were quite close. These results revealed that the estimating accuracy could be truly optimized only if the original value of the unit cost was considered directly.

Table 5 The estimating accuracy achieved by two methods
Full size table

Subsequently, the FCI method proposed by Chen [11] was also applied to the real case for a second comparison, in which two experts constructed two FNNs to estimate the unit cost of the DRAM product with a TFN. The inputs to either FNN were the unit costs within the L previous periods, and the output was the fuzzy unit cost estimate within the current period. All of them were normalized values. The FNNs tried to fit the log-sigmoid value, instead of the original or logarithmic value, of the unit cost. Either expert determined the average satisfaction level on the left-hand side (\( s_{L} (k) \)), the average satisfaction level on the right-hand side (\( s_{R} (k) \)), and the average range of the fuzzy unit cost estimates (\( \psi (k) \)), as summarized in Table 6. The estimation results from the two experts are summarized in Fig. 8.

Table 6 Parameters specified by experts
Full size table
Fig. 8
figure 8

The estimating results by two experts using Chen’s [11] method

Full size image

Subsequently, FI and an RBF were applied to determine the narrowest range and to derive the representative value of the unit cost, respectively. The results are shown in Fig. 9.

Fig. 9
figure 9

The aggregation results

Full size image

The estimating performance using Chen’s [11] method was evaluated as:

Average range = 0.554

Hit rate = 80%

MAE = 0.102

MAPE = 7.4%

RMSE = 0.141

The new FCI approach surpassed Chen’s [11] method in improving the average range, MAE, and MAPE. Conversely, Chen [11] performed slightly better than the new FCI approach with regard to RMSE, which was not unexpected since the FNNs used in Chen’s [11] method aimed to minimize the RMSE.

To ascertain whether the advantage of the new FCI approach over the existing methods was statistically significant, the performances of all methods along each dimension were ranked. Then, the ranks of each method along all dimensions were summed up. The results are shown in Table 7. The proposed methodology surpassed the other methods.

Table 7 A comparison of the performances of various methods along all dimensions
Full size table

The FCI method proposed by Chen and Chiu [13] was based on agents and therefore was not compared in this study.

Subsequently, the new FCI approach was applied to another case to further elaborate its effectiveness. The second case contained the unit cost data of a DRAM product within 12 periods that are shown in Fig. 10. The collected data were cut in half for model building and testing. Two experts collaborated to estimate the unit cost of the product. The models chosen by the two experts were

Fig. 10
figure 10

The unit cost data of another case

Full size image

Expert I: PPII (\( o(1) = 3 \), \( m(1) = 2 \), \( d(1) = 0. 64 \))

Expert II: PPI (\( o(2) = 2 \), \( s(2) = 0. 3 3 \))

The solving of the PP problems led to the following fuzzy unit cost learning models:

$$ \tilde{C}_{t} (1) = ( 1. 0 1 8 0,\; 1. 2 9 6 1,\; 1. 5 5 7 2){\text{e}}^{{\frac{(0. 8 4 9 9,\;0. 8 4 9 9,\;0. 8 4 9 9)}{t}}} , $$
(73)
$$ \tilde{C}_{t} (2) = ( 1. 2 3 6 8,\; 1. 3 9 8 5,\; 1. 6 6 6 4){\text{e}}^{{\frac{(0. 4 7 7 0,\;0. 4 7 7 0,\;0. 4 7 7 0)}{t}}} , $$
(74)

The unit cost estimates by the two experts were aggregated using the FI-BPN approach. The aggregation results were compared with actual values in Fig. 11. The estimation performance was evaluated as follows:

Fig. 11
figure 11

The aggregation results

Full size image

MAE = 0.049

MAPE = 3.6%

MAPE = 0.056

The average range = 0.405

which showed a very good fit that supported the effectiveness of the new FCI approach.

Conclusions

Reducing the unit cost of each product is a goal that is pursued by every factory. However, the results of cost reduction actions are often overestimated, resulting in unreliable and misleading unit cost estimates that undermine financial or production planning. To resolve this problem and to enhance the effectiveness of unit cost estimation, a new FCI approach is proposed in this study. The new FCI approach is novel because it handles the original value, rather than the logarithmic or log-sigmoid value, of the unit cost directly, unlike existing methods. Such a treatment is believed to be a viable way to truly optimize the precision or accuracy of the unit cost estimation.

The proposed new FCI approach and two existing methods were applied to a real DRAM case, from which the following observations were made:

  1. 1.

    The estimating precision, measured in terms of the average range for the testing data using the new FCI approach, was 2% better than that using Chen’s [10] method, and 20% better than that using Chen’s [11] method, respectively.

  2. 2.

    The new FCI approach also outperformed the two existing methods in improving the estimating accuracy, especially with regard to MAE and MAPE.

In future research, the treatments taken in this study can be applied to modify other FCI methods. The new FCI approach should also be applied to other types of products or learning processes in other fields, such as productivity learning [2], energy efficiency learning [17], etc., to further elaborate on its effectiveness. These learning processes are often subject to uncertainty. The application of the proposed methodology is able to deal with such uncertainty and model the learning process precisely. Further, there are various types of learning curve models, such as log-linear and non-log-linear learning curve models [19]. The proposed methodology can be modified to be suitable for modeling other types of learning curve models.