Skip to main content

Advertisement

SpringerLink
Log in

Combining Pumping Flowrate Maximization from Polluted Aquifers with Cost Minimization

  • Original Article
  • Published:
Environmental Processes Aims and scope Submit manuscript

Abstract

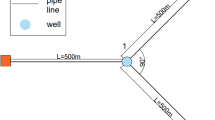
In this paper, we present a methodology for optimal management of aquifers affected by non-conservative pollutants, by means of application examples. Our multi-criteria approach takes into account: a) Maximization of safe total flowrate from a system of wells; and b) Minimization of pumping cost or of pipe network construction cost. As a preliminary step, we have studied maximization of the total safe well flowrate, without cost restrictions, in order to calculate an upper flowrate bound for all application examples. Then, we have solved two sets of minimization problems, using one of the aforementioned cost criteria in the respective objective function and different values of the required total safe well flowrate as a constraint in all of them. In this way, we have derived a set of Pareto optimal solutions for each problem. We have used the method of genetic algorithms as optimization technique and a moving point code for the simulation of advective pollutant transport. Our paper includes also: a) a discussion of relevant technical details, i.e., moving point arrival at production wells and structure of the penalty function, which is used in the genetic algorithm code; and b) a comparison of the results of the two sets of examples, which shows that the optimal well layouts are rather similar for large total safe flowrate values, while they are quite different for small ones.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  • Anders R, Chrysikopoulos CV (2005) Virus fate and transport during artificial recharge with recycled water. Water Resour Res 41(10):W10415. https://doi.org/10.1029/2004WR003419

    Article  Google Scholar 

  • Bauer-Gottwein P, Schneider R, Davidsen C (2016) Optimizing wellfield operation in a variable power price regime. Groundwater 54:92–103

    Article  Google Scholar 

  • Bauser G, Franssen H-JH, Stauffer F, Kaiser H-P, Kuhlmann U, Kinzelbach W (2012) A comparison study of two different control criteria for the real-time management of urban groundwater works. J Environ Manag 105:21–29

    Article  Google Scholar 

  • Dorini GF, Thordarson FÖ, Bauer-Gottwein P, Madsen H, Rosbjerg D, Madsen H (2012) A convex programming framework for optimal and bounded suboptimal well field management. Water Resour Res 48:W06525. https://doi.org/10.1029/2011WR010987

    Article  Google Scholar 

  • Etsias G (2016) Optimization of groundwater resources management in polluted aquifers. Master thesis, Dept. of Civil Engineering, Aristotle University of Thessaloniki, Greece

  • Heydari F, Saghafian B, Delavar M (2016) Coupled quantity-quality simulation-optimization model for conjunctive surface-groundwater use. Water Resour Manag 30(12):4381–4397

    Article  Google Scholar 

  • Holland JH (1975) Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor

    Google Scholar 

  • Karamagiola E, Katsifarakis KL (2007) An approximate solution to convective-dispersive mass transport in aquifers. In: Proc. CEMEPE 2007, Skiathos, Greece, pp 2627–2632

  • Katsifarakis KL, Karpouzos DK (2012) Genetic algorithms and water resources management: an established, yet evolving, relationship. In: Katsifarakis KL (ed) Hydrology, hydraulics and water resources management: a heuristic optimisation approach. WIT Press, Southampton, pp 7–37

  • Katsifarakis KL, Latinopoulos P (1995) Efficient particle tracking through internal field boundaries in zoned and fractured aquifers. In: Wrobel LC and Latinopoulos P (eds) Water pollution III: modelling, measuring and prediction, Proc 3rd Int. Conf. WATER POLLUTION 95 (Porto Carras, Greece). Computational Mechanics Publications, Southampton, pp 41–48

  • Katsifarakis KL, Latinopoulos P, Petala Z (1999) Application of a BEM and moving point code to the study of pumped coastal aquifers. In: Brebbia CA, Power H (eds) Boundary elements XXI. WIT Press, Southampton, pp 639–647

  • Katsifarakis KL, Mouti M, Ntrogkouli K (2009) Optimization of groundwater resources management in polluted aquifers. Global Nest 11(3):283–290

    Google Scholar 

  • Ketabchi H, Ataie-Ashtiani B (2015) Evolutionary algorithms for the optimal management of coastal groundwater: a comparative study toward future challenges. J Hydrol 520:193–213

    Article  Google Scholar 

  • Khadem M, Afshar MH (2015) A hybridized GA with LP-LP model for the management of confined groundwater. Groundwater 53(3):485–492

    Article  Google Scholar 

  • Kontos YN (2013) Optimal management of fractured coastal aquifers with pollution problems. PhD thesis, Dept. of Civil Engineering, Aristotle University of Thessaloniki, Greece (in Greek)

  • Kontos YN, Katsifarakis KL (2012) Optimization of management of polluted fractured aquifers using genetic algorithms. European Water 40:31–42

    Google Scholar 

  • Mani A, Tsai FT, Kao S-C, Naz BS, Ashfaq M, Rastogi D (2016) Conjunctive management of surface and groundwater resources under projected future climate change scenarios. J Hydrol 540:397–411

    Article  Google Scholar 

  • Matiaki MC, Siarkos I, Katsifarakis KL (2016) Numerical modeling of groundwater flow to delineate spring protection zones. The case of Krokos aquifer, Greece. Desalin Water Treat 57(25):11572–11581

    Article  Google Scholar 

  • Nicklow J, Reed P, Savic D, Dessalegne T, Harrell L, Chan-Hilton A, Karamouz M, Minsker B, Ostfeld A, Singh A, Zechman E (2010) State of the art for genetic algorithms and beyond in water resources planning and management. J Water Resour Plan Manag 136(4):412–432

    Article  Google Scholar 

  • Ogata A, Banks RB (1961) A solution of the differential equation of longitudinal dispersion in porous media. Prof. paper 411-A, U.S. Geological Survey

  • Sidiropoulos E, Tolikas P (2008) Genetic algorithms and cellular automata in aquifer management. Appl Math Model 32(4):617–640

    Article  Google Scholar 

  • Singh A, Panda SN (2013) Optimization and simulation modelling for managing the problems of water resources. Water Resour Manag 27(9):3421–3431

    Article  Google Scholar 

  • Sreekanth J, Datta B (2011) Coupled simulation-optimization model for coastal aquifer management using genetic programming-based ensemble surrogate models and multiple-realization optimization. Water Resour Res 47(4). https://doi.org/10.1029/2010WR009683

  • Staboultzidis A-G, Dokou Z, Karatzas GP (2017) Capture zone delineation and protection area mapping in the aquifer of Agia, Crete, Greece. Environ Process. https://doi.org/10.1007/s40710-017-0221-3

  • Stampouli A (2016) Optimal management of polluted aquifers aiming at maximization of safe total flowrate and minimization of network construction cost. Master thesis, Dept. of Civil Engineering, Aristotle Univesity of Thessaloniki, Greece (in Greek)

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Aristotle University of Thessaloniki, 54124, Thessaloniki, Greece

    G. Etsias & K. L. Katsifarakis

Authors
  1. G. Etsias
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. L. Katsifarakis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to K. L. Katsifarakis.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Etsias, G., Katsifarakis, K.L. Combining Pumping Flowrate Maximization from Polluted Aquifers with Cost Minimization. Environ. Process. 4, 991–1012 (2017). https://doi.org/10.1007/s40710-017-0264-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40710-017-0264-5

Keywords

Search

Navigation