Abstract
The Kunwari River Basin (KRB) needs effective management of water resources for sustainable agriculture and flood hazard mitigation. The Soil and Water Assessment Tool (SWAT), a semi distributed physically based model, was chosen and set up in the KRB for hydrologic modeling. SWAT-CUP (SWAT-Calibration and Uncertainty Programs) was used for model calibration, sensitivity and uncertainty analysis, following the Sequential Uncertainty Fitting (SUFI-2) technique. The model calibration was performed for the period (1987–1999), with initial 3 years of warm up (1987–89); then, the model was validated for the subsequent 6 years of data (2000–2005). To assess the competence of model calibration and uncertainty, two indices, the p-factor (observations bracketed by the prediction uncertainty) and the r-factor (achievement of small uncertainty band), were taken into account. The results of SWAT simulations indicated that during the calibration the p-factor and the r-factor were reported as 0.82 and 0.76, respectively, while during the validation the p-factor and the r-factor were obtained as 0.71 and 0.72, respectively. After a rigorous calibration and validation, the goodness of fit was further assessed through the use of the coefficient of determination (R2) and the Nash–Sutcliffe efficiency (NS) between the observed and the final simulated values. The results indicated that R2 and NS were 0.77 and 0.74, respectively, during the calibration. The validation also indicated a satisfactory performance with R2 of 0.71 and NS of 0.69. The results would be useful to the hydrological community, water resources managers involved in agricultural water management and soil conservation, as well as to those involved in mitigating natural hazards such as droughts and floods.
Similar content being viewed by others
1 Introduction
Water resources management problems involve complex processes from the surface and subsurface level to their interface regimes (Sophocleous 2002; Srivastava et al. 2013b). The hydrogeologic characteristics within the watershed system are heterogeneous in nature with respect to time and space (Blöschl and Sivapalan 1995; Strayer et al. 2003), making water resources management very challenging. Distributed hydrological watershed models are very useful and effective tools in water resources management (Patel and Srivastava 2013, 2014), particularly in assessing the impacts, effects and influence of land use/land cover and climate change on water resources (Narsimlu et al. 2013; Patel et al. 2012; Srivastava et al. 2008, 2013a). Several other applications, for example hydrological impact of forest fires, have also been assessed for runoff prediction and water balance using the SWAT model (Batelis and Nalbantis 2014).
Among semi-distributed hydrological models, SWAT model was originally developed for prediction of discharge from ungauged basins (Arnold et al. 1998). SWAT model with a spatial database has been successfully used to simulate flows, sediment, and nutrient loadings of a watershed (Rosenthal and Hoffman 1999). SWAT has been extensively used in many countries worldwide for discharge prediction as well as for soil and water conservation (Patel and Srivastava 2013; Spruill et al. 2000; Zhang et al. 2010). Fiseha et al. (2014) have applied SWAT for the study of the hydrological responses to climate change in the Upper Tiber River basin using bias corrected daily Regional Climate Model (RCM) outputs. Srinivasan et al. (2010) have evaluated the SWAT model performance for hydrologic budget and crop yield simulations in Upper Mississippi River Basin without calibration (ungauged basin). Gosain et al. (2006) have applied SWAT for hydrological modeling of 12 major river basins in India, namely the Ganga, the Cavery, the Krishna, the Godavari and the Mahanadi, among others. Spruill et al. (2000) have calibrated and validated SWAT model in a small experimental watershed in Kentucky, USA and stated that monthly flows were predicted more accurately. Arnold and Allen (1996) have successfully validated surface runoff, groundwater flow, groundwater recharge parameters in three Illinois watersheds. Further, Santhi et al. (2006) have performed an extensive validation of SWAT over two watersheds in Texas (USA).
Now a days, evaluation of parameter uncertainty has gained popularity in sciences, including hydrological sciences (Beck 1987; Beven and Binley 1992; Yatheendradas et al. 2008), biosciences (Blower and Dowlatabadi 1994), atmospheric sciences (Derwent and Hov 1988), and structural sciences (Adelman and Haftka 1986). In the present study, a hydrological modeling procedure was carried out using SWAT model to quantify water balance and to estimate the dynamics of hydrology. Model calibration and validation have been evaluated through sensitivity analysis (SA) and uncertainty analysis (UA) (Blasone et al. 2008; Srivastava et al. 2013d; Wagener and Wheater 2006; Zheng and Keller 2007). The technique of model calibration is a challenging and rigorous process, which depends on the number of input parameters, model complexity as well as iterations (Vanrolleghem et al. 2003). SA and UA are essential processes to reduce the uncertainties imposed by the variations of model parameters and structure (Gupta et al. 2006; Srivastava et al. 2013c; Wagener and Gupta 2005). Recently developed calibration and uncertainty analysis techniques for watershed models include: MCMC (Markov Chain Monte Carlo) method (Vrugt et al. 2008), GLUE (Generalized Likelihood Uncertainty Estimation) (Beven and Binley 1992), ParaSol (Parameter Solution) (Yang et al. 2008), and SUFI-2 (Sequential Uncertainty Fitting) (Abbaspour et al. 2004). These techniques (GLUE, Parasol, SUFI-2 and MCMC) have been linked to SWAT model through SWAT-CUP algorithm (Abbaspour et al. 2007), and enable SA and UA of model parameters as well as structure (Rostamian et al. 2008). Studies on model calibration and UA have emphasized and confirmed that SWAT model is an effective tool in managing water resources (Tang et al. 2012). Abbaspour et al. (2004) and Yang et al. (2008) applied the SUFI-2 technique for evaluation of SWAT model. The SUFI-2 technique needs a minimum number of model simulations to attain a high-quality calibration and uncertainty results (Yang et al. 2008).
With this background, the main objective of this study was to simulate the streamflow of the Kunwari River Basin (KRB) using SWAT model integrated with model calibration and uncertainty analysis by means of SUFI-2 algorithm and to evaluate its applicability for KRB. This modeling study also provides support to water resource managers in effectively planning and managing agricultural water resources, soil erosion, as well as natural disasters.
2 Materials and Methods
2.1 Study Area
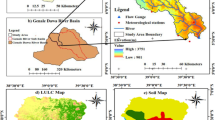
Kunwari River (also spelled as Kuwari or Kwari River) is a river flowing in Morena and Bhind district provinces of Madhya Pradesh State in Central India. KRB is a sub-basin of Sind River Basin, located between latitudes 24° 58′ 18″ N to 27° 02′ 58″ N and longitudes 76° 45′ 40″ E to 79° 31′ 45″ E (Fig. 1). It is mainly an agricultural watershed with a drainage area of 6821 km2. The altitude varies from 100 m asl in the southwest part to 467 m asl in the northeast part, with a mean of 222 m asl and a standard deviation of 76 m. Major crops in this area are wheat, sorghum, soya bean, gram, mustard, rice, sunflower and millet. Most of the annual precipitation falls during the monsoon period, i.e., from June to September, ranging from 750 to 1400 mm. Maximum temperature in April and May ranges from 38 to 44 °C, whereas the minimum temperature occurs during the months of December and January ranging from 7 to 13 °C.
2.2 Datasets
SWAT was used in this study to derive the parameters that have control on the hydrologic processes of the KRB. Topography, land use, soil, weather and hydrology databases were collected from different sources/agencies and are listed in Table 1. The detailed land use/land cover map is provided in Fig. 2, and the areas of each land use type and classification system are shown in detail in Table 2. The details of all the datasets used in this study are summarized in the following sections.
Land use/land cover map of Kunwari River Basin (refer to Table 2 for legend)
2.2.1 Land Use/Land Cover and Soil Properties
The land use/land cover (LULC) dataset is used to understand the hydrological processes and governing system (Singh et al. 2014; Srivastava et al. 2012). Crop specific digital layers for the preparation of LULC map have been obtained from the National Remote Sensing Centre (NRSC), Hyderabad, India. The main land uses in the KRB have been classified as agriculture (52.47 %), followed by wasteland/brusland (22.93 %), barren land (10.53 %), deciduous forest (4.35 %), grassland/rangelands (3.67 %), water bodies (0.41 %) and urban with medium density (0.35 %). Another important layer for understanding hydrological response is soil type and texture (Paudel et al. 2014; Srivastava et al. 2014). The major soil groups are alluvial soils mixed in red and black. The colours of these soils are pale yellow to yellowish brown in Bhind and parts of Morena district. The surface texture varies from sandy loam to loam, clay loam and even to clay. The alleviation of finer particles ensures fine texture of the middle horizons. Soils are neutral to alkaline in soil reaction.
2.2.2 Digital Elevation Model (DEM)
The Digital Elevation Model (DEM) helps in understanding the flow behavior and flow pattern. Further, it also plays an important role in fast and slow runoff processes (Patel et al. 2013; Wagener and Wheater 2006; Yadav et al. 2013). In this study, 90 m × 90 m SRTM digital layer (DEM) was obtained from the USGS (http://srtm.usgs.gov/) and has been used as SWAT input for watershed delineations and topographic parameterization (Fig. 1). The KRB has been divided into 20 sub-basins and 271 Hydrological Response Units (HRUs) based on uniform soil, land use and slope with a threshold area of 15,000 ha. The two reservoirs have been identified on the main stream of the KRB and used with the Arc SWAT interface.
2.3 SWAT-CUP Model
SWAT is a semi-distributed, watershed scale, continuous time model that operates on a daily time series and evaluates the land management practices impacts on water, sediment and agricultural chemical yields in unguaged basins (Arnold et al. 1998). This model is capable of uninterrupted simulation over a long period of time. SWAT can simulate flows (surface and subsurface), sediment, pesticide and nutrient movement through the hydrologic cycle of the watershed system. The hydrologic processes within the model comprise infiltration, percolation, evaporation, plant uptake, lateral flows and groundwater flows including snowfall and snowmelt (Neitsch et al. 2005). The Modified SCS (Soil Conservation Service) curve number (CN) method is used for the estimation of surface runoff volume (Mishra and Singh 2003). Lateral flow is simulated by kinematic storage model and return flow is estimated by creating a shallow aquifer (Arnold et al. 1998). Channel flood routing is predicted by the Muskingum method and transmission losses, evaporation, return flow etc., are adjusted for estimation of outflow from a channel (Baymani-Nezhad and Han 2013). The water balance Eq. (1), which governs the hydrological components of SWAT model (Neitsch et al. 2005), is as follows
where: SW t is the final soil water content (mm); SW 0 is the initial soil water content on day i (mm); R day is the amount of precipitation on day i (mm); Q surf is the amount of surface runoff on day i (mm); E a is the amount of evapotranspiration (ET) on day i (mm); W seep is the amount of water entering the vadose zone from the soil profile on day i (mm); Q gw is the amount of return flow on day i (mm).
The process of SWAT automatic calibration includes uncertain model parameters, model simulations and extraction of output results (Bekele and Nicklow 2007; Eckhardt and Arnold 2001). The major components of the model include weather, hydrology, soil erosion, soil temperature and land management practices (Arnold and Allen 1996). SWAT divides the basin into sub-basins with chosen threshold area and joined by the stream network. Further, these sub-basins are divided into HRUs with unique attributes of land cover, slope and soils (Patel and Srivastava 2013). These HRUs are non-spatially distributed and account for diversity in SWAT model. HRU demarcation can reduce the SWAT runs by lumping similar soil and land use areas into a single unit (Neitsch et al. 2005).
2.4 SUFI-2 Algorithm
SWAT-CUP is specially developed by Abbaspour et al. (2007) to interface with the SWAT model. Any calibration/uncertainty or sensitivity program can easily be linked to SWAT model by using this generic interface. In this study, the SUFI-2 algorithm was used to investigate sensitivity and uncertainty in streamflow prediction. A multiple regression system with Latin hypercube samples by means of objective function values was used in calculating the responsive parameter sensitivities, with the detailed method specified by Yang et al. (2008). Different ways of formulating an objective function may lead to different results (Legates and McCabe 1999).
Several objective functions have been used for estimating model performance, which include the Root Mean Square Error (RMSE), the absolute difference, the logarithm of differences, the R2, the Chi-square and the Nash-Sutcliffe Efficiency (NS). Several objective functions have been utilized to reduce the non-uniqueness problem in the model characterization (Duan et al. 2006). The average changes in the objective functions were estimated based on the consequential changes and sensitivity of each parameter, referred to here as the relative sensitivities. It provides partial information about the sensitivity of the objective function and is based on linear approximation of the model parameters. Further, to estimate the level of significance between the datasets, a t-test was applied to identify the relative significance of each parameter. The t-test and the p-values were used to provide a measure and the significance of the sensitivity, respectively. The larger absolute values are more sensitive than the lower ones, while a value closer to zero has more significance. Robustness of the SUFI-2 algorithm was tested through the SA with and without observations.
2.5 Performance Indices
Four parameters have been used for evaluation of model performance, namely R2, NS, p-factor and r-factor. The R2 and NS were used as a likelihood measure for the rainfall runoff model (SWAT model) following the SUFI-2 approach between the observed and predicted streamflow. The NS (Nash and Sutcliffe 1970) was calculated using the following Eq. (2):
where: x i are the ground-based measurements; y i are the model predicted data; and \( \overline{x} \) is the mean of the ground-based measurements.
The p-factor (percentage of measured data bracketed by the 95 % prediction boundary), often referred to as 95PPU, was used to quantify all the uncertainties associated with the SWAT model. The Latin hypercube sampling method was employed for 95PPU and for obtaining the final cumulative distribution of the model outputs. These are calculated at the level of 2.5 and 97.5 % prediction limit. During the initialisation of model parameters, SUFI-2 assumes a large parameter uncertainty and then decreases this uncertainty through the p-factor and the r-factor performance statistics. The range of the p-factor varies from 0 to 1, with values close to 1 indicating a very high model performance and efficiency, while the r-factor is the average width of the 95PPU band divided by the standard deviation of the measured variable and varies in the range 0–1 (Abbaspour et al. 2007; Yang et al. 2008). The p- and r-factors are closely related to each other, which indicates that a larger p-factor can be achieved only at the expense of a higher r-factor. After balancing these two factors, and at an acceptable value of the r- and p-factors, the calibrated parameter ranges can be generated. The r-factor is given by Eq. (3) (Yang et al. 2008):
where: \( {y}_{t_i,97.5\%}^M \) and \( {y}_{t_i,2.5\%}^M \) are the upper and lower boundaries of the 95UB; and σ obs is the standard deviation of the observed data.
3 Results and Discussion
3.1 Evaluation of Hydro-meteorological Datasets
The comparisons among the time series of rainfall, ET, and streamflow demonstrate a high temporal consistency with seasons and follow a strong seasonal cycle, peaking normally from July to September. Typically, a very high rainfall and streamflow occurs during the period of September. The periods of August-September have witnessed the maximum rainfall intensities, which was connected with some moderately high-duration storms. The period of March-April was slightly drier compared to other months, as suggested by high ET and low rainfall. The period May-August witnessed a progressive drying of the soil because of rising temperature, which leads to high evaporation. The low discharge is obtained in the period from November to January due to lesser rainfall (Fig. 3). The behavior of ET indicates that quite lower values were obtained during the winter season, however, after the mid of April, a gradual increase can be seen in the graph. Increasing ET during the summer was attributed to high solar radiation and temperature, which lead to development of high soil moisture deficit. The study indicates that in this catchment the rainfall and discharge are very responsive to each other with similar pattern over the entire study period. Some higher ET values, also obtained during the period July to September, could be due to strong influence by net radiation and temperature.
The Mann-Kendall trend analysis was applied on weather datasets to find out the existing trends in rainfall, ET and streamflow. Figure 3 shows the mean monthly observed data with the highest and lowest values of streamflow, ET and rainfall. If the probability (p’) is less than the significant value (0.05) of α (alpha) then the Null hypothesis (Ho) is rejected, which means that there is a trend in the time series and suggests that the results are statistically significant. Further, if the p’-value is more than the significant value of α, then the Ho is accepted, which means that there is no trend in the times series which indicates insignificant results. If the p’-value is less than 10 % or 0.01 then the trend is significant and if this value is more than 0.01 then the trend is insignificant. The Mann-Kendall Score (S) values with negative sign indicate a decreasing trend whereas values with positive sign show an increasing trend. According to the values in Table 3, rainfall has shown an increasing trend in the months of January, April, May, June and December, while in the other months it shows a decreasing trend. Overall, the annual trend for the rainfall is decreasing with time. Similarly for streamflow, the monthly and annual trends were found decreasing with time. In case of discharge, the decreasing trend was observed for the months of February, August, September and December.
3.2 Model Initialization
In defining HRUs, the minor land use/land cover, slope and soil types were ignored by setting a threshold of 10 %, to avoid unnecessary large number of HRUs in the analysis (Neitsch et al. 2005). SWAT has been calibrated for monthly streamflow by comparing with the observed streamflow at the Bhind gauge station located near the outlet of KRB. The model was run for a period of 18 years (1987–2005) by considering the first 3 years as warm up time of the model. The period 1990–1999 was used for calibration (see Fig. 4a), whereas the remaining 6 years of the dataset, i.e., 2000–2005, were employed for validating the model (see Fig. 4b). The SWAT-CUP (calibration and uncertainty programs) have been applied for model sensitivity, calibration and uncertainty analysis.
In this work, we have provided a rigorous calibration based on sensitivity analysis of model parameters (Abbaspour et al. 2007), following the SWAT-CUP documentation (Neitsch et al. 2005). For calibration of SWAT model, a total of 18 SWAT parameters were selected for model calibration and uncertainty analysis for streamflow prediction based on earlier studies and SWAT documentation (Neitsch et al. 2002).
3.3 Model Calibration and Sensitivity Analysis
Dotty plots were used here to depict the sensitivity of the model parameters used for the calibration of SWAT (Fig. 5). These are the results of model run with NS as an objective function during calibration. The dotty plot conditioned in SUFI-2, and all these sampled parameter sets were taken as behavioral samples with the NS threshold value of 0.5. When a sharp and clear peak is observed for the parameter, it can be treated as parameter with highest likelihood. Similarly, the insensitive parameters were obtained by diffused peak represented by cumulative distributions, which in turn indicate that parameter was less skilled in discharge prediction in KRB. The SA of model parameters indicated that some lower performances may be caused by structural inadequacies in model components. The results indicate that, most of the observations with different parameters are bracketed by the 95PPU (for NS value 0.6 to 0.8), signifying that SUFI-2 is capable of capturing the model behavior. The SWAT simulations results look satisfactory for the prediction of discharge, and the final parameter ranges were the best solution obtained for the KRB. Most of the observed values during the calibration and validation were within the boundaries of 95PPU, which indicates that SWAT model uncertainties were falling within the permissible limits. Hence, this calibrated model can be used for different applications, such as impact on streamflow in KRB of climate change, water resources planning and management, and LULC changes.
Table 4 presents the summary and details of the parameters being applied for sensitivity analysis. The results of SA have confirmed that all the 18 sensitive parameters are considered to be applicable to surface runoff, groundwater, channel routing, snow processes, and soil properties. A number of SWAT model parameters were used in model calibration, which include CN2, ALPHA_BF, GWQMN, ESCO, CH_K2, CH_N2, REVAPMN, SOL_AWC, HRU_SLP, SOL_K, SOL_BD, SLSUBBSN, GW_REVAP, EPCO, GW_DELAY, SFTMP, ALPHA_BNK and OV_N. Additional details about these parameters are provided in Table 4. In this study, the result of global sensitivity analysis with the t-test indicates that the most sensitive parameters are ALPHA_BNK, ESCO followed by CH_K2 and CN2.
3.4 Uncertainty in Streamflow Prediction
The performance indices for the model parameters were derived using a window size of monthly time steps and are shown in Table 5. The calibration results (Fig. 4a) revealed that the observed peak values in years 1992 and 1995, and during validation in 2003, were not falling under 95PPU band. This may be due to the reason that the SWAT model is unable to simulate extreme events and under predicts the large flows in KRB (Tolson and Shoemaker 2007). It is concluded from Fig. 4a–b that the key information regarding the model parameters emerged during the wet periods only. During the calibration period from 1990 to 1999, the p-factor was 0.82 and the r-factor was 0.76, and through the validation from 2000 to 2005 they were obtained as 0.71 and 0.72, respectively (Table 5). The percentage of observed data being bracketed by 95PPU during calibration was 82 % and during validation 76 %, which indicates a good performance of the model (Fig. 4). The reduction in 95PPU (p-factor) from 0.82 to 0.71 during validation (Fig. 4b) indicates the uncertainties in input driving variables such as rainfall. Careful examination of calibration and validation results showed that the observed data is not falling under 95PPU band at the base flow part. This may be due to the limitation of SWAT model for simulating groundwater flow (Rostamian et al. 2008). The parameter uncertainties were acceptable, when the parameter ranges of the p-factor and the r-factor reach the desired limits. Further, goodness of fit can be quantified by the R2 and NS (Nash and Sutcliffe 1970) between the observed and the final simulated data. According to Nash and Sutcliffe (1970), when the NS value is greater than 0.75, the simulation results are good, and when NS is greater than 0.36, the simulation results are satisfactory. For the results during the calibration period, the values of R2 and NS obtained were 0.77 and 0.74, respectively, while during validation the R2 and NS values obtained were 0.71 and 0.69, respectively, which indicates that the model can be accepted for KRB. The probable reasons for some low performance at some parts of the model could be attributed to rainfall, which was measured at only one gauge station. For such a large area generally one gauge station is not sufficient. Hence, this can be considered as a major limitation of this study.
4 Conclusions
For hydrological prediction, such as discharge, a careful model calibration is required for an efficient result. For a good modeling practice, it is required to report the uncertainties in the model prediction along with the results. In this study, SWAT model was applied in the KRB to simulate streamflow in the period 1987 to 2005 by following a rigorous calibration and validation analysis using the SUFI-2 technique. SUFI-2 is a popular algorithm which estimates the sensitivity and uncertainty of a hydrological model. Thus, it is beneficial in communicating fairly accurate results to the end-users and in obtaining persuasive model predictions. The outcomes of the sensitivity and uncertainty analysis using SWAT and SUFI-2 indicate that the model is appropriate for streamflow prediction in the KRB. The results of this study indicate that the SWAT-CUP is useful in forecasting flow and estimating underlying uncertainties and related assumptions in the field of water resources. Based on the final results of calibration and validation, the model has closely simulated the observed streamflow. The results of this study would be practical in agricultural water management and soil and water conservation, as well as in mitigating natural hazards such as drought and flood. This calibrated model can be used in further assessment of climate change and land use/land cover impact assessment on water resources. It is suggested in future studies, to use more uncertainty techniques in model calibration, sensitivity and uncertainty analysis.
References
Abbaspour K, Johnson C, van Genuchten MT (2004) Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J 3:1340–1352
Abbaspour K, Vejdani M, Haghighat S (2007) SWAT-CUP calibration and uncertainty programs for SWAT. In: MODSIM 2007 International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand, 2007
Adelman HM, Haftka RT (1986) Sensitivity analysis of discrete structural systems. AIAA J 24(5):823–832. doi:10.2514/3.48671
Arnold J, Allen P (1996) Estimating hydrologic budgets for three Illinois watersheds. J Hydrol 176:57–77
Arnold JG, Srinivasan R, Muttiah RS, Williams JR (1998) Large area hydrologic modeling and assessment - part I: model development. J Am Water Resour Assoc 34:73–89
Batelis SC, Nalbantis I (2014) Potential effects of forest fires on streamflow in the Enipeas river basin, Thessaly, Greece. Environ Process 1(1):73–85. doi:10.1007/s40710-014-z
Baymani-Nezhad M, Han D (2013) Hydrological modeling using effective rainfall routed by the Muskingum method (ERM). J Hydroinf 15(4):1437–1455, 10.2166/hydro.2013.007
Beck M (1987) Water quality modeling: a review of the analysis of uncertainty. Water Resour Res 23:1393–1442
Bekele EG, Nicklow JW (2007) Multi-objective automatic calibration of SWAT using NSGA-II. J Hydrol 341:165–176
Beven K, Binley A (1992) The future of distributed models: model calibration and uncertainty prediction. Hydrol Process 6:279–298
Blasone R-S, Madsen H, Rosbjerg D (2008) Uncertainty assessment of integrated distributed hydrological models using GLUE with Markov chain Monte Carlo sampling. J Hydrol 353:18–32
Blöschl G, Sivapalan M (1995) Scale issues in hydrological modelling: a review. Hydrol Process 9:251–290
Blower S, Dowlatabadi H (1994) Sensitivity and uncertainty analysis of complex models of disease transmission: an HIV model, as an example. International Statistical Review/Revue Internationale de Statistique:229–243
Derwent R, Hov Ø (1988) Application of sensitivity and uncertainty analysis techniques to a photochemical ozone model. J Geophys Res 93:5185–5199
Duan Q, Schaake J, Andreassian V, Franks S, Goteti G, Gupta HV, Gusev YM, Habets F, Hall A, Hay L, Hogue T, Huang M, Leavesley G, Liang X, Nasonova ON, Noilhan J, Oudin L, Sorooshian S, Wagener T, Wood EF (2006) Model parameter estimation experiment (MOPEX): an overview of science strategy and major results from the second and third workshops. J Hydrol 320:3–17
Eckhardt K, Arnold J (2001) Automatic calibration of a distributed catchment model. J Hydrol 251:103–109
Fiseha B, Setegn S, Melesse A, Volpi E, Fiori A (2014) Impact of climate change on the hydrology of upper Tiber River Basin using bias corrected regional climate model. Water Resour Manag 28:1327–1343
Gosain A, Rao S, Basuray D (2006) Climate change impact assessment on hydrology of Indian river basins. Curr Sci 90:346–353
Gupta HV, Beven KJ, Wagener T (2006) Model calibration and uncertainty estimation. Encycl Hydrol Sci 11:131
Legates DR, McCabe GJ (1999) Evaluating the use of “goodness of fit” measures in hydrologic and hydroclimatic model validation. Water Resour Res 35:233–241
Mishra SK, Singh V (2003) Soil conservation service curve number (SCS-CN) methodology. Vol 42. Springer 516p
Narsimlu B, Gosain AK, Chahar BR (2013) Assessment of future climate change impacts on water resources of upper Sind river basin, India using SWAT model. Water Resour Manag 27:3647–3662. doi:10.1007/s11269-013-0371-7
Nash JE, Sutcliffe J (1970) River flow forecasting through conceptual models: part I—a discussion of principles. J Hydrol 10:282–290
Neitsch SL, Arnold JG, Kiniry J, Srinivasan R, Williams JR (2002) Soil and water assessment tool user manual. Texas Water Resources Institute, College Station, TWRI Report TR-192
Neitsch SL, Arnold J, Kiniry J, Williams J, King K (2005) Soil and water assessment tool theoretical documentation version 2005 Texas, USA
Patel D, Srivastava P (2013) Flood hazards mitigation analysis using remote sensing and GIS: correspondence with town planning scheme. Water Resour Manag 27:2353–2368. doi:10.1007/s11269-013-0291-6
Patel DP, Srivastava PK (2014) Application of geo-spatial technique for flood inundation mapping of low lying areas. In: Remote Sensing Applications in Environmental Research. Springer, pp 113–130
Patel DP, Dholakia MB, Naresh N, Srivastava PK (2012) Water harvesting structure positioning by using geo-visualization concept and prioritization of mini-watersheds through morphometric analysis in the Lower Tapi Basin. J Indian Soc Remote Sens 40:299–312
Patel DP, Gajjar CA, Srivastava PK (2013) Prioritization of Malesari mini-watersheds through morphometric analysis: a remote sensing and GIS perspective. Environ Earth Sci 69:2643–2656
Paudel D, Krishna Thakur J, Kumar Singh S, Srivastava PK (2014) Soil characterization based on land cover heterogeneity over a tropical landscape: an integrated approach using earth observation datasets. Geocarto Int:1–55
Rosenthal W, Hoffman D (1999) Hydrologic modelings/GIS as an aid in locating monitoring sites. Trans ASAE 42:1591–1598
Rostamian R, Jaleh A, Afyuni M, Mousavi SF, Heidarpour M, Jalalian A, Abbaspour KC (2008) Application of a SWAT model for estimating runoff and sediment in two mountainous basins in central Iran. Hydrol Sci J 53:977–988
Santhi C, Srinivasan R, Arnold JG, Williams J (2006) A modeling approach to evaluate the impacts of water quality management plans implemented in a watershed in Texas. Environ Model Softw 21:1141–1157
Singh S, Srivastava P, Gupta M, Thakur J, Mukherjee S (2014) Appraisal of land use/land cover of mangrove forest ecosystem using support vector machine. Environ Earth Sci 71:2245–2255. doi:10.1007/s12665-013-2628-0
Sophocleous M (2002) Interactions between groundwater and surface water: the state of the science. Hydrogeol J 10:52–67
Spruill C, Workman S, Taraba J (2000) Simulation of daily and monthly stream discharge from small watersheds using the SWAT model. Trans ASAE 43:1431–1439
Srinivasan R, Zhang X, Arnold J (2010) SWAT ungauged: hydrological budget and crop yield predictions in the Upper Mississippi River Basin. Trans ASABE 53:1533–1546
Srivastava P, Mukherjee S, Gupta M (2008) Groundwater quality assessment and its relation to land use/land cover using remote sensing and GIS. Proceedings of International Groundwater Conference on Groundwater Use - Efficiency and Sustainability: Groundwater and Drinking Water Issues, Jaipur, India:19–22
Srivastava PK, Han D, Ramirez MR, Bray M, Islam T (2012) Selection of classification techniques for land use/land cover change investigation. Adv Space Res 50:1250–1265
Srivastava PK, Han D, Ramirez MR, Islam T (2013a) Appraisal of SMOS soil moisture at a catchment scale in a temperate maritime climate. J Hydrol 498:292–304
Srivastava PK, Han D, Ramirez MR, Islam T (2013b) Machine learning techniques for downscaling SMOS satellite soil moisture using MODIS land surface temperature for hydrological application. Water Resour Manag 27:3127–3144
Srivastava PK, Han D, Rico-Ramirez MA, Al-Shrafany D, Islam T (2013c) Data fusion techniques for improving soil moisture deficit using SMOS satellite and WRF-NOH land surface model. Water Resour Manag 27:5069–5087
Srivastava PK, Han D, Rico-Ramirez MA, Islam T (2013d) Sensitivity and uncertainty analysis of mesoscale model downscaled hydro-meteorological variables for discharge prediction. Hydrol Process. doi:10.1002/hyp.9946
Srivastava PK, Han D, Rico-Ramirez MA, O’Neill P, Islam T, Gupta M (2014) Assessment of SMOS soil moisture retrieval parameters using tau–omega algorithms for soil moisture deficit estimation. J Hydrol 519(Part A):574–587. doi:10.1016/j.jhydrol.2014.07.056
Strayer DL, Ewing HA, Bigelow S (2003) What kind of spatial and temporal details are required in models of heterogeneous systems? Oikos 102:654–662
Tang J, Yang W, Z-y L, J-m B, Liu C (2012) Simulation on the inflow of agricultural non-point sources pollution in Dahuofang reservoir catchment of Liao river. J Jilin Univ 42:1462–1468
Tolson BA, Shoemaker CA (2007) Cannonsville reservoir watershed SWAT2000 model development, calibration and validation. J Hydrol 337:68–86
Vanrolleghem PA et al (2003) A comprehensive model calibration procedure for activated sludge models. Proc Water Environ Fed 2003:210–237
Vrugt JA, Ter Braak CJ, Clark MP, Hyman JM, Robinson BA (2008) Treatment of input uncertainty in hydrologic modeling: doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour Res 44
Wagener T, Gupta HV (2005) Model identification for hydrological forecasting under uncertainty. Stoch Env Res Risk A 19:378–387
Wagener T, Wheater HS (2006) Parameter estimation and regionalization for continuous rainfall-runoff models including uncertainty. J Hydrol 320:132–154
Yadav SK, Singh SK, Gupta M, Srivastava PK (2013) Morphometric analysis of Upper Tons basin from Northern Foreland of Peninsular India using CARTSAT satellite and GIS. Geocarto Int :1–38
Yang J, Reichert P, Abbaspour K, Xia J, Yang H (2008) Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J Hydrol 358:1–23
Yatheendradas S, Wagener T, Gupta H, Unkrich C, Goodrich D, Schaffner M, Stewart A (2008) Understanding uncertainty in distributed flash flood forecasting for semiarid regions. Water Resour Res 44:W05S19
Zhang X, Srinivasan R, Liew MV (2010) On the use of multi‐algorithm, genetically adaptive multi-objective method for multi-site calibration of the SWAT model. Hydrol Process 24:955–969
Zheng Y, Keller AA (2007) Uncertainty assessment in watershed-scale water quality modeling and management: 1. Framework and application of generalized likelihood uncertainty estimation (GLUE) approach. Water Resour Res 43: doi:10.1029/2006WR005345
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Narsimlu, B., Gosain, A.K., Chahar, B.R. et al. SWAT Model Calibration and Uncertainty Analysis for Streamflow Prediction in the Kunwari River Basin, India, Using Sequential Uncertainty Fitting. Environ. Process. 2, 79–95 (2015). https://doi.org/10.1007/s40710-015-0064-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40710-015-0064-8