1 Introduction

Nepal is endowed with approximately 6,000 rivers that drain about 222 billion m3 of water annually into the sea (Sharma and Awal 2013). The perennial nature of rivers and the steep topography provide a great potential to tap this resource for hydropower generation. It is no surprise that Nepal relies heavily on hydroelectric projects, especially run-of-the-river (R-o-R) facilities, for electricity generation. The theoretical power generation potential was estimated to be 83,500 MW in 1966, out of which 42,000 MW is technically and economically feasible to be produced (Jha 2010). In reality, Nepal has so far managed to generate only 665.11 MW, which is less than 1 % of what is economically feasible, and 2 % of the total energy consumption in the country. Despite harboring a huge hydropower potential, Nepal has not been able to meet its own domestic demand for electricity with its resources. As a result, the country is currently going through a severe energy crisis. Consequently, each year, power cuts are increasing at an alarming rate. The power outage was around 12 h/day in 2009–10 and 2010–11, and steeply rose to 14 h/day in 2011–12 (Sharma and Awal 2013). The hydropower production reaches its full installed capacity during the monsoon period but declines to 16.66 % of the installed capacity during the dry months (Paudyal and Shrestha 2010). The discrepancy in power production arises due to the RoR type of the hydropower, where power production is guided by river discharge, which is generally high during the monsoon and low during the rest of the months.

In order to alleviate the magnitude of power outage and to promote the hydropower sector, the Government of Nepal first developed a policy plan in 2008 in order to generate 10,000 MW in 10 years (2010–2020) and 25,000 MW in 20 years (2010–2030) (Pradhan 2009). Following this, a significant number of hydroelectric projects are under construction and many are in the pipeline. Some of these new projects are modeled on storage-type hydropower plants (e.g., Budhi Gandaki, Kali Gadaki II, Upper Seti, Nalsyaugad, Tamor). Some of the ambitious projects, such as Chisapani-Karnali (10,800 MW), Pancheswor (6480 MW), Budhi Gandaki (600 MW), and Sapta Koshi High Dam (3600 MW) are facing uncertainty due to financial and political crisis gripping the country at present.

The hydropower projects in Nepal are conceived taking into consideration only the short-term hydro-meteorological data, thus neglecting the impacts of climate change on hydropower generation and its impact on power plant operation in the future. Recent studies have pointed to an increase in temperature over the years, with remarkable warming at high altitudes (Bhutiyani et al. 2010). While the global average temperature increased by approximately 0.75 °C in the last century (IPCC 2007), the Himalayan region of Nepal witnessed an increase of 0.15 °C to 0.6 °C per decade in the last three decades. Similarly, there has been a significant change in precipitation (volume and pattern) as well. The precipitation data observed at 80 stations show a decreasing trend for most of the areas in southern and western Nepal. In contrast, the hilly and mountainous regions of western Nepal and north-eastern Nepal are experiencing an increase in precipitation as per the recorded data. Climate change affects different aspects of local hydrology, such as the magnitude and pattern of water availability in rivers, and water quality, which ultimately have an effect on the operation of reservoirs and hydropower production. The assessment of how climate change impacts water resources, would, therefore, be crucial for sustainability of any long-term water resources utilization projects. There exists only limited knowledge about the impact of climate change on water resources in the hills and mountains of Nepal (Sharma and Shakya 2006). It is important to understand climate change scenarios in terms of variation in temperature, precipitation and river flow for efficient planning of hydropower and obtaining maximum power generation capacity (Pathak 2010). Considering the changes brought about by climate change in Nepal, a clear understanding of climatic variability and change is very important for the development and management of the hydropower sector in the long run.

The Kulekhani-I is the only reservoir-type hydroelectric power station in Nepal with an installed capacity of 60 MW, with two units of 30 MW each. But, this powerhouse was designed to be only a peaking power station that acts as an emergency standby station during peak load. The expected annual energy generation capacity of this plant is 165 GWH as primary energy and 46 GWH as secondary energy, contributing with about 7 % to the Integrated Nepal Power System (INPS).

This study investigates the potential impact of climate change on the hydrology of the Kulekhani watershed, and assesses its consequences on the hydropower production of Kulekhani hydropower project. Climate change scenarios are developed based on outputs of selected global circulation models (GCMs); the impact of climate change on hydrology of the watershed and change in future powerproduction are analyzed.

2 Study Area and Data Description

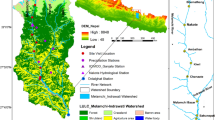
This study was carried out in Kulekhani watershed and the Kulekhani hydropower project, which lies in the Bagmati River Basin (BRB) of Nepal. With a total area of about 125 km2, the watershed extends approximately between 27°30′00″N and 27°40′46″N latitude and 85°1′41″ E and 85°13′56″ E longitude. It is located about 50 km southwest of the capital city Kathmandu (Ghimire 2004) with an altitude varying from 1534 to 2621masl at the peak of Simbhanjyang.

The climate of Kulekhani watershed varies from subtropical atlower elevations to temperate at higher elevations. The watershed experiences four distinct seasons: pre-monsoon (March to May), monsoon (June to September), post-monsoon (October to November) and winter (December to February). The warm temperate humid zone is found between 1500 and 2000 masl and the cool temperate humid zone lies above 2000 masl. The average annual precipitation over the watershed is about 1500 mm. May to September is the wettest period whereas the winter is a distinctively dry period. The average temperature in the warm temperate humid zone is 15 °C to 20 °C and in the cool temperate humid zone 10 °C to 15 °C (Ghimire 2004).

Two different watersheds are part of this hydropower project: the Kulekhani watershed, which is one of the tributaries of Bagmati River, and the Upper Rapti watershed. The dam is located in the Kulekhani watershed whereas the powerhouse (an underground type) is located in the Upper Rapti watershed at an altitude of 900 masl, and is connected with the reservoir by a headrace tunnel of 6 km in length and a penstock pipe of 1.3 km. The water for power generation is released into the Mandu River, one of the tributaries of Rapti, through a tail race tunnel 1 km in length.

Kulekhani watershed is further divided into six major sub-watersheds (Fig. 1), all of which contribute inflows into the 7-km long Kulekhani reservoir, a 114-m high rock fill dam that supplies water for hydropower generation downstream. The natural runoff of the Kulekhani river at the dam site is as low as 2.1 m3/s in the dry months and 6.2 m3/s in the wet months. Therefore, the runoff during the wet months is stored in the reservoir to ensure power generation during the dry months. The total storage capacity of Kulekhani reservoir is 85.3 million m3 (MCM). Of this capacity, 12.0 MCM is allocated to dead storage and the remaining capacity 73.3MCM becomes live storage. This project was designed for an expected life time of 100 years with an expected annual sedimentation rate of 700 m3/km2/year (Nippon Koei Co. Ltd. 1983). The rule curve of this hydropower projectwas designed by Nippon Koei Co. Ltd in Nippon Koei Co. Ltd 1983 based on the existing facilities and energy demand. The rule curve stipulates a higher release from the reservoir in the dry months and a lower release at the beginning of the wet months.

Fig. 1
figure 1

Location map of the Kulekhani watershed showing three rainfall stations and discharge gauging station

Full size image

Daily rainfall data were collected from Nepal’s Department of Hydrology and Meteorology (DHM). In addition, the daily rainfall data of three nearby stations (Thankot, Chisapani and Daman), which have the longest available data, were collected for different available time periods. Maximum and minimum temperature data collected from DHM was available only for the Daman station. The daily discharge data required for calibration and validation of the hydrological model were collected for Kulekhani discharge gauging station for the period 1973–1977. The monthly reservoir level data required to calculate the power generation of the hydropower were collected for the period 1998–2011 and the monthly electricity generation data were collected for the period 1982–2009 (Table 1).

Table 1 Summary of hydro-meteorological and other relevant data used in the study
Full size table

3 Materials and Methods

Future climate data from for the SRES A2 and B2 scenarios in the HadCM3 model were used from 2010 to 2099 (CCCSN 2012). The A2 scenario describes a very heterogeneous world with regionally oriented economic development, and an average surface warming of 2–5.4 °C, whereas the B2 scenario portrays a heterogeneous world with local solutions and environmental sustainability, where the expected rise in the surface warming is 1.4–3.8 °C (Nakicenovic et al. 2000). The observed precipitation and temperature data for the baseline period and downscaled GCM data for baseline and future periods were used as the input for the hydrological model HEC-HMS ver. 3.5 in order to estimate river discharge. The simulated river discharge time series were then input in the reservoir simulation model, Hec-ResSim, to estimate the change in the reservoir levels and power generation in future periods. The overall methodology applied in this study is presented in Fig. 2.

Fig. 2
figure 2

Flowchart illustrating the methodological framework

Full size image

3.1 Prediction of Future Climate Scenarios

3.1.1 Selection of GCM

In this study, we chose the climate data derived from the HadCM3 GCM, a coupled atmospheric–ocean general circulation model (CCCSN 2012), as suggested by Babel et al. (2013) and Shrestha et al. (2013). Based on the result of statistical performance analysis of five GCMs (CCSR/NIES, CGCM3, CSIRO, ECHAM4 and HadCM3) carried out by Babel et al. (2013), the HadCM3 model has been considered as the most suitable GCM to project the future climate of Bagmati River Basin (BRB). The HadCM3 performed comparatively better than other GCMs, presenting a higher value of coefficient of determination (R2), lower root mean square error (RMSE) and standard deviation (SD), making it statistically the most reliable GCM in simulating present-day climate in the BRB. The statistical analysis was carried out to simulate temperature and precipitation in the BRB and for comparison of the results with the observed climatic variables gathered from monthly average data from 1990 to 2005. Since, some of the GCMs provide data starting from 1990 and only the monthly average data are publicly accessible from most of the GCMs, the monthly average data for the period 1990–2005 was used in statistical analysis.

3.1.2 Downscaling of GCM Data

The downscaling of temperature and precipitation is done using the Statistical DownScaling Model (SDSM) (Wilby et al. 2002) by regressing the observed data obtained from National Centers for Environmental Prediction (NCEP) reanalysis data and GCM outputs from HadCM3 for the A2 and B2 scenarios. The SDSM model was applied in precipitation and temperature data from the three meteorological stations located in the study area (Fig. 1), in order to project the future precipitation and temperature for three future periods: 2010–2039, 2040–2069 and 2070–2099. The monthly calibration of SDSM for each station is done by developing a relationship between large-scale screened predictor variables and the observed data. The unconditional option was used for temperature whereas the conditional option was used for calibrating precipitation. The list of predictors and predictands (local scale surface variables) used for the calibration is shown in Table 2. As the predictors vary from station to station, the calibration was done separately for each station (Daman, Chisapani and Thankot). The observed historical data for the time period 1961–1990 is used for calibration of precipitation for all three stations, and the data of the time period 1971–2000 is used for calibrating the temperature of the Daman station. The period 2001–2005 was chosen for validating the temperature results, while the period 1991–2000 was used for validating the precipitation results. Next, statistical analysis was carried out to compare the mean daily, maximum monthly and standard deviation values of the observed and the simulated data.

Table 2 Summary of selected predictor variables and their respective predictands
Full size table

3.1.3 Predicting Future River Discharge

In order to simulate river discharge, the semi-distributed hydrologic modeling system HEC-HMS version 3.5, developed by the United States Army Corps of Engineers (USACE-HEC 2006), was used. The overall model setup consists of two components, HEC-GeoHMS and HEC-HMS, which simulate surface runoff based on precipitation data. The watershed model was developed in HEC-GeoHMS and later imported to the HEC-HMS watershed model in this study.

3.2 Hydrological Modelling

3.2.1 Watershed Delineation

Delineation of the watershed and development of stream network was performed using HEC-GeoHMS in ArcGIS 10. Basic parameters such as watershed area, centroid of each sub-watershed, slope, channel length, longest discharge path, and gage weight, which are required to calculate other parameters of the hydrological model, were derived from watershed delineation. The input data required for this process is the digital elevation model (DEM). The DEM preprocessing in this study was done by using ArcHydro tool. The 30 m resolution DEM of Bagmati Basin was downloaded from ERSDAC website (http://www.gdem.aster.ersdac.or.jp/).

3.2.2 HEC-HMS Model Setup and its Performance Evaluation

The HEC-HMS 3.5 model was used to simulate the precipitation runoff processes of the watershed. The areas sub-basins, stream network, and other basin properties were generated using HEC-GeoHMS and were later imported to HEC-HMS model. The basin model was developed using deficit and constant loss method, Clark unit hydrograph, constant monthly base flow and lag methods. After completing the basin model, the meteorological model was developed using Thiessen polygon gage weight, created using HEC-Geo HMS. Thiessen polygons were constructed based on the rainfall gage point and basin polygon. The Thiessen polygon gage weights for sub-basin were based on three different precipitation stations (i.e., Daman, Thankot, Chisapani). The basin average precipitation at each sub-basin was calculated according to Thiessen polygon weights. The model generates the runoff from precipitation taking into consideration the topography, soil and landuse characteristics, as well as the climatic variables like evapotranspiration, after which water availability in the watershed at present and in predicted future climate scenarios was projected. Clark’s unit hydrograph model was used in the study for each sub-watershed. The unit hydrograph in this method is developed using the two parameters, time of concentration (tc) and storage coefficient (R). The time of concentration is defined as the time water takes to travel from the farthermost point in the watershed to the watershed outlet (Sabol 1988). HEC-GeoHMS is used for the calculation of the longest discharge path. The average slope of each sub-watershed and tc were calculated using Kirpich’s formula (Kirpich 1940). Both tc and R depend on the topography of the watershed and are in the range 0.1–500 h and 0–150 h, respectively. tc and R were determined using the following equations (1) and (2), respectively:

$$ {t}_{\mathrm{c}}=\frac{0.0195{(L)}^{0.77}}{S^{0.385}} $$
(1)

where L is the length of the longest discharge path (m), S the slope of the watershed, and t c is the time of concentration (min).

The approximation of the storage coefficient was made using the following relation derived by Graf et al. (1982):

$$ {\frac{R}{R+t}}_c=\beta $$
(2)

where β is the coefficient whose value is assumed to be 0.75 for mountainous regions.

The calibration was done to estimate some of the parameter used in model of HEC-HMS which cannot be estimated by observation or measurement of channel or watershed characteristics. Calibration improves the performance of the model. The HEC-HMS rainfall-runoff model in the study was calibrated and validated by comparing the observed daily flow recorded at the inlet of the Kulekhani reservoir with the flow simulated by the model. The model calibration was done using three-year data (1973–1975) and the model was validated with the data for 1977 as discharge data were available till 1978; these were recorded for the design of Kulekhani hydropower project. The performance of the calibrated and validated model was checked using three statistical indices: the coefficient of determination (R2), the percentage volume error (PVE), and the Nash-Sutcliffe efficiency (NSE), which are defined as follows.

The coefficient of determination (R2) gives the proportion of the variance (fluctuation) of one variable that is predictable from the other variable. The value of R2 varies from 0 (poorest result) to 1 (best result), with higher values indicating less error and, typically, values greater than 0.5 considered acceptable.

$$ {R}^2=\frac{{\displaystyle \sum \Big({Q}_0-\overline{Q_0}}\Big)-\left({Q}_S-{\overline{Q}}_S\right)}{\sqrt{{\displaystyle \sum \Big({Q}_0-\overline{Q_0}}\Big){}^2-{\left({Q}_S-{\overline{Q}}_S\right)}^2}} $$
(3)

where Q0 is observed discharge, \( \overline{Q_0} \) is average observed value, QS is simulated discharge and \( \overline{Q_s} \) is average simulated value.

The Percentage Volume Error (PVE) is the ratio of difference between the calibrated volume (Vc) and the observed volume (V0) to the observed volume, as presented in Equation (4). It is expressed as a percentage and as a lower value of PVE to indicate a good fit between the computed and observed data:

$$ PVE=\frac{V_{\mathrm{c}}-{V}_0}{V_0} $$
(4)

The Nash–Sutcliffe Efficiency (NSE) (Nash & Sutcliffe Nash and Sutcliffe 1970) is widely used and isa highly reliable method to evaluate the analytical power of hydrological models. It is given by the equation:

$$ NSE=1-\frac{{\displaystyle \sum_1^t{\left({Q}_0-{Q}_C\right)}^2}}{{\displaystyle \sum_1^t\Big(}{Q}_0-{\overline{Q}}_0\Big){}^2} $$
(5)

where Q0, \( \overline{Q_0} \) and Q C are observed discharge, average observed discharge and computed discharge, respectively.

The value of NSE ranges between 0 and 1. A value of 1 indicates a perfect fit and 0 a poor fit. NSE values between 0.50 and 0.95 point to a good simulation result (Andersen et al. 2001).

3.3 Simulating Reservoir Operation

HEC-ResSim (USACE 2007), developed by the Hydrologic Engineering Center of the US Army Corps of Engineers, was used to simulate the reservoir operation. For making release decisions, the original real-time rule-curve is used in the model to meet operating requirements for power generation, flood control, water supply, environmental release, and other demands. The model simulates reservoir operations by taking into account all the physical and hydraulic characteristics of a reservoir.

HEC-ResSim consists of three sets of modules - watershed setup, reservoir network, and simulation - that provide access to specific types of data within a watershed. The watershed is digitally represented in the watershed setup module using different tools such as stream alignment tool, reservoir tool, diversion tool, etc. In reservoir network module, different inputs are provided to describe the physical and operational systems of the reservoir. Finally, the simulation module is used to construct and model the simulation and review the results. The reservoir in this study was simulated for three different future time periods and climatic conditions.

4 Results and Discussion

4.1 Performance of SDSM

Table 3 provides values for both R2 and RMSE for assessing model performance for monthly minimum and maximum temperature for Daman station and precipitation for Daman, Chisapani and Thankot. The R2values above 0.5 and RMSE less than 1.22 °C were accepted to calibrate and validate the SDSM model for downscaling temperature. In a similar way for downscaling the precipitation, the SDSM model was calibrated and validated with acceptance of R2 valuesexceeding 0.5 and RMSE below 18.23 mm.

Table 3 Performance of SDSM during calibration and validation period
Full size table

4.2 Projection of Future Temperature

The projected relative change in the mean of both maximum and minimum temperature at Daman station for three time periods 2010–2039, 2040–2069 and 2070–2099 (2020s, 2050s, and 2080s, respectively) for both A2 and B2 scenarios with respect to base period 1971–2000 is shown in Fig. 3. Our analysis shows that maximum temperature keeps increasing every month except for January, July and August. Similarly, minimum temperature also increases every month except for the month of January. The results show that the highest increase in maximum temperature is 1.5 °C and 1.1 °C for the A2 and B2 scenarios, respectively, for 2080s. Monthly analysis indicates that the highest rise of mean maximum temperature takes place in November and a decreasing trend of this variable is seen in January and August, for both scenarios A2 and B2. Similarly, the highest rise in minimum temperature is observed to be 2.4 °C and 1.6 °C for A2 and for B2 scenarios, respectively, for 2080s. The mean minimum temperature will rise highest in October and drops lowest in January for both A2 and B2 scenarios.

Fig. 3
figure 3

Line graph showing the monthly average temperature and bar graph showing the relativechange in temperature with respect to baseline period a) for maximum temperature and b) for minimum temperature

Full size image

4.3 Projection of Future Precipitation

The monthly projected precipitation for the three future time periods 2020s, 2050s and 2080s relative to the baseline period (1980s) does not indicate any fixed trend for both A2 and B2 scenarios. However, the projected precipitation showed both spatial and temporal variation. The relative changes are calculated by deducting the precipitation of baseline period from the projected precipitation, as presented in Table 4. A decrease in annual precipitation is observed for the Daman and Thankot stations, while it increases at the Chisapani station, for both A2 and B2 scenarios. During the wet months (May to September), a decrease in average precipitation for all the watersheds is observed in June and August by almost 5 % and 2 %, respectively, for both A2 and B2 scenarios (Fig. 4). An irregular change in precipitation was observed for both scenarios. However, the average annual watershed precipitation decreasesfor all three time periods in the A2 scenariobut varies over future time periods. It decreases for 2020s and 2080s, with some increase in 2050s (Fig. 4).

Table 4 Percentage change in annual precipitation for different station relative to baseline period (1980s) for A2 and B2 scenarios
Full size table
Fig. 4
figure 4

Bar graph showing relative change in basin average monthly precipitation for the future periods with baseline period (1980s) and line graph showing the basin average monthly precipitation for baseline period for a) A2 scenario and b) B2 scenario

Full size image

4.4 Calibration and Validation of the HEC-HMS

During the calibration, it was found that the storage coefficient, the initial deficit, and the constant loss parameters are more important in adjusting water balance, whereas the time of concentration, the lag time and the storage coefficient play an important role in determining the time to peak. The R2 and NSE values were 0.81, 0.59 for calibration, and 0.75 and 0.58 for the validation period, respectively. The water volume was overestimated by 0.09 % during the calibration period and underestimated by 9 % during the validation period. The peak discharges and base flows closely matched during calibration and validation, especially with regard to the number of peak events and the magnitude of the peak. However, the time to peak did not fit perfectly with the observed data and some overestimation of peak discharge can be observed (Fig. 5). Thus, it is established that the model is capable of simulating the discharge in the Kulekhani River with good precision. This calibrated and validated model was then used for simulating discharge in baseline and future periods.

Fig. 5
figure 5

Comparison of observed and simulated flow at Kulekhani discharge gauging station for calibration period (1Jan1973- 31Dec1975) and validation period (1Jan1977- 31Dec1977)

Full size image

4.5 Climate Change Impact Assessment and Analysis of River Discharge

4.5.1 Impact on Monthly Average River Discharge

The changes in monthly average discharge (as a percentage) for future time periods for both A2 and B2 scenarios against the baseline period are presented in Table 5. In the A2 scenario, the discharge was found to be decreased for two wet months (June and August) while it was found to be increased for May, July and September. During the dry period (October to April) except for November, March and April the discharge was found to increase throughout the year. The changes varied from −29.3 % in November to 53.7 % in December (2050s). The result suggests the possibility of decreased discharge in the A2 scenario in the wet months. However, the discharge seems to be increasing in the dry months as per predictions for the future.

Table 5 Percentage changes in monthly average flow in future for A2 and B2 scenarios with respect to base period of Kulekhani discharge gauging station (1980s)
Full size table

In the B2 scenario, the wet months (May –September) witnessed a decrease in discharge in June and August whereas the discharge increased in May, July and September. In the dry months, the discharge increased in all the months (October to April) except for November and April. The average monthly discharge for three future time periods for both A2 and B2 scenarios are plotted to understand the change in discharge against the base period (Fig. 6). A small amount of decrease in monthly discharge was predicted for June and August in the future for both scenarios, whereas a significant increase in discharge can be noticed in some months (February, March, October) in the B2 scenario and also in December in both scenarios. However, the overall pattern of discharge throughout the year remained the same with maximum flow in July for the base period and all three future time periods (Fig. 6a). A decrease in average flow during the monsoon months (June, August) in future time periods indicates a significant reduction in reservoir storage as compared to the baseline period. Similar results, indicating a possibility of decrease in monsoon discharge were obtained by Sharma and Shakya (2006) while conducting a study on the entire Bagmati River Basin.

Fig. 6
figure 6

Monthly projected average flow in Kulekhani discharge gauging station for (a) A2scenario and (b) B2 scenario

Full size image

4.5.2 Flow Duration Curve

A flow-duration curve was prepared with the monthly discharge simulated from HEC-HMS model averaged over 30 years for the baseline period and future time periods for both A2 and B2 scenarios (Fig. 7). The estimated firm energy and secondary energy for each time period are shown in Table 6. The total energy predicted by the model was lower than the energy generated in actual practice, which is due to the limitation of the downscaling model to project the extreme precipitation events, which in fact, play a vital role in reservoir storage. When compared, the total annual energy production of 91.14 GWh in the baseline period is expected to decrease by 3 GWh in 2080s. However, the model predicts an increase in the energy production during 2050s for the A2 scenario. Likewise, the total energy is expected to increase in the future to 96 GWh during the 2080s under the B2 scenario. Most interestingly, it can be observed that the firm energy is diminishing for both scenarios, which clearly indicates a reduction of minimum discharge of the river.

Fig. 7
figure 7

Flow duration curve for base period and future time period of Kulekhani discharge gauging station for (a) A2 scenario and (b) B2 scenario

Full size image
Table 6 Firm energy, secondary energy and total energy according to the flow duration curve for different time periods under A2 and B2 scenario
Full size table

4.6 Reservoir Simulation Using HEC-ResSim

4.6.1 Hydrological, Physical and Operational Data

Reservoir inflow data is one of the major inputs of HEC-ResSim model. Daily river discharge data predicted by HEC-HMS for both A2 and B2 scenarios in all the three time periods were used for this study. The elevation-area-storage curve, and the type and capacity of each outlet were used as the physical reservoir data with power characteristics such as installed capacity (60 MW), total head loss of 2 m, overall efficiency of 85 % and average tail water elevation of 916 masl, retrieved from the design report of the Kulekhani I hydropower plant. Three major water management pool levels were considered, namely, inactive zone, the conservation zone and the flood control zone.

4.6.2 Climate Change Impact on Reservoir Water Level and Energy Generation

HEC-ResSim simulations are performed under sevendifferent operatingtime settings. In the first six settings, the power plant was operated for the same time period throughout the year. The operating times established are 3 h/d, 4 h/d, 6 h/d, 8 h/d, 10 h/d and 12 h/d. In the last setting, the power plant was operated for different time periods in dry and wet months: 10 h/d for dry months and 3 h/d for wet months. The changes in total annual power generation, monthly power generation, and water levels against the base period were computed for 2020s, 2050s and 2080s for both A2 and B2 scenarios.

4.6.3 Water Level in the Reservoir

Change in water level in the reservoir with different operating times for both scenarios is shown in Fig. 8. A similar curve for reservoir water level can be seen for all the future time periods in both A2 and B2 scenarios. All the simulations were performed following the same rule curve as shown in Fig. 8. We can observe that, for operation times 3, 4, 6, and 7 h/d, the reservoir level does not meet the lowest level given by the rule curve. However, when the plant is operated for 10 h/d in dry months and 3 h/d in wet months, the reservoir level faithfully follows the rule curve during the dry months. However, the inflows to the reservoir in the wet season in not enough to maintain the reservoir level to follow the rule curve during the wet season. Thus, operating the reservoir more on dry months and less during wet months can help in storing the water for dry months as targeted. It can be concluded that the operating time period of 3 h/d for wet months and 10 h/d for dry months is the best operating time period from which maximum energy can be generated for all future time frames and climate scenarios.

Fig. 8
figure 8

Change in water level in reservoir during power generation for different operating time, climate scenario and future timeframe with respect to rule curve

Full size image

4.7 Future Energy Generation

The total annual energy generated under different simulation conditions are shown in Table 7. When the simulations were performed assuming constant operating time period of 3 and 4 h/d, respectively, throughout the year, an almost uniform level of energy of 4 GWh and 6 GWh was generated for each month. When the operating time period was increased to 6 h/d and more, with full reservoir at the beginning of the year, the energy generation declined. The decrease in energy generation is because of no possibility of refilling of the reservoir for the next year as the inflow in the wet season is not sufficient for storage while fulfilling the demand of the required hours of operation. When the power plant is operated for 8, 10 and 12 h/d, a maximum of up to 19 GWh is generated for the first few months from January to May but for the remaining months, the energy generation declines to as low as 4 GWh. The release of water from reservoir to the power plant under this scenario is almost the same at the early months of the year, and the generation is high, but for the remaining months, the inflow is not sufficient to follow the existing rule curve.

Table 7 Annual total energy generation by the power plant for future timeframes with A2 and B2 scenarios for different reservoir operation times and their percentage change (% ch.) as compared with baseline average annual energy generation
Full size table

In the last operation setting, the power plant is operated for different time periods in wet and dry months. In dry months, it is operated for 10 h/d and in wet months for 3 h/d. Under this scenario, the energy generated in May to November (wet months) is far less than that generated in the dry period. While comparing the future monthly energy generation at 8 different cases of assumed operating time period, the maximum monthly energy was generated in the month of February in B2 scenario of 2050s which is 24.09 GWh. This energy was generated while running hydropower for uniform time period of 10 h/d throughout the year. Similarly, the minimum monthly energy was generated in month of June in A2 scenarios of both 2020s and 2080s, which is 4.4 GWh. This was generated while running hydropower for 3 h/d throughout the year.

The total annual power generation for different operating time periods in 2020s, 2050s and 2080s under scenarios A2 and B2 is presented in Table 7. In addition, the percentage change in power generation is calculated against the total annual power generation of 143 GWh in the baseline period (1982–2009). While comparing all the cases, the maximum energy is generated when the plant is operated for 10 h/d in the dry months and 3 h/d in the wet months. Compared to the baseline energy generation, the average energy generation may decrease by at least 30 % in both A2 and B2 scenarios in the future. The least reduction in power generation (8–13 %), when compared to the baseline scenario, is observed when the reservoir is operated for 10 h/d in the dry months and 3 h/d in the wet months. The maximum total annual energy generated in this case is 131.23 GWh for B2 in 2050s, while the minimum total energy generated is 125 GWh for A2 in 2080s.

5 Conclusions

The main objective of this study was to assess the impact of climate change on water resources in the Kulekhani watershed and its impact on hydropower generation in the Kulekhani Hydropower project in Nepal. We have downscaled future precipitation and temperature data from HadCM3 GCM, and subsequently, used that data as input to simulate river discharge in the Kulekhani River for baseline and future periods. This discharge was then used to simulate the energy production for different hours of operation of power plant per day for wet and dry months.

The maximum and minimum temperatures were found to increase for most months under both A2 and B2 scenarios. The highest rise in minimum temperature was more than that for maximum temperature, which indicates that the watershed is also increasingly warmed. Precipitation was found to increase in Chisapani station and decrease in Daman and Thankot stations.

The change in river discharge under both scenarios did not show any fixed trend. Future runoff in the watershed decreases for two months (June and August) during the wet months, and for most months during the dry month period, the discharge increases under both scenarios. HEC-ResSim model was used to simulate the hydropower production under different operating times under future climate scenarios. Assuming a hydropower operation time of 7 h/d during the baseline period (1982–2009), the average power production may decrease by at least 30 % under both A2 and B2 scenarios in the future. However, the maximum energy generation was observed when the reservoir is operated for 10 h/d in the dry months and 4 h/d in the wet months, reducing the power generation only by 8–13 % compared to the baseline period.

The rule curve of Kulekhani hydropower was developed in 1982 when the country was not facing any power outage problem and also there was not much of a gap between electricity demand and supply. Therefore, operating the reservoir following the same rule curve becomes difficult to match the water release in all months in the future. Therefore, revising the rule curve of the Kulekhani hydropower is essential to maintain or increase the power production under climate change scenarios in the Kulekhani watershed.