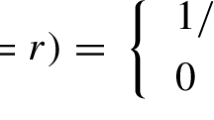Sato–Tate distributions of twists of the Fermat and the Klein quartics

Abstract

We determine the limiting distribution of the normalized Euler factors of an abelian threefold A defined over a number field k when A is ${\overline{\mathbb Q}}$-isogenous to the cube of a CM elliptic curve defined over k. As an application, we classify the Sato–Tate distributions of the Jacobians of twists of the Fermat and Klein quartics, obtaining 54 and 23, respectively, and 60 in total. We encounter a new phenomenon not visible in dimensions 1 or 2: the limiting distribution of the normalized Euler factors is not determined by the limiting distributions of their coefficients.

1 Introduction

Let A be an abelian variety of dimension $g\ge 1$ defined over a number field k. For a prime $\ell$, let $V_\ell (A):=\mathbb Q\otimes \varprojlim _n\!\!\! A[\ell ^n]$ be the (rational) $\ell$-adic Tate module of A, and let

$$\begin{aligned} \varrho _{A}:G_k\rightarrow {\text {Aut}}(V_\ell (A)) \end{aligned}$$

be the $\ell$-adic representation arising from the action of the absolute Galois group $G_k$ on $V_\ell (A)$. Let $\mathfrak {p}$ be a prime of k (a nonzero prime ideal of the ring of integers ${\mathcal O}_k$) not lying above the rational prime $\ell$. The L-polynomial of A at the prime $\mathfrak {p}$ is defined by

$$\begin{aligned} L_\mathfrak {p}(A,T):=\det (1-\varrho _A({\text {Frob}}_\mathfrak {p})T;\,V_\ell (A)^{I_\mathfrak {p}})\in \mathbb Z[T], \end{aligned}$$

where ${\text {Frob}}_\mathfrak {p}$ denotes a Frobenius element at $\mathfrak {p}$ and $I_\mathfrak {p}$ is the inertia subgroup at $\mathfrak {p}$; it does not depend on the choice of $\ell$. Let S be a finite set of primes of k that includes all primes of bad reduction for A and all primes lying above $\ell$. For $\mathfrak {p}\not \in S$ the polynomial $L_\mathfrak {p}(A,T)$ has degree 2g and coincides with the numerator of the zeta function of the reduction of A modulo $\mathfrak {p}$. The L-function of A is defined as the analytic continuation of the Euler product

$$\begin{aligned} L(A,s):=\prod _\mathfrak {p}L_\mathfrak {p}(A,N(\mathfrak {p})^{-s})^{-1}, \end{aligned}$$

where $N(\mathfrak {p}):=[{\mathcal O}_k\!:\!\mathfrak {p}]$ is the (absolute) norm of $\mathfrak {p}$. The normalized L-polynomial of A at $\mathfrak {p}$ is the monic polynomial $\overline{L}_\mathfrak {p}(A,T):=L_ \mathfrak {p}(A,N(\mathfrak {p})^{-1/2}T)\in \mathbb R[T]$; its roots come in complex conjugate pairs and lie on the unit circle, as shown by Weil in [36].

As constructed by Serre in [26], the Sato–Tate group $\mathrm {ST}(A)$ is a compact real Lie subgroup of $\mathrm {USp}(2g)$, defined up to conjugacy in $\mathrm {GL}_{2g}(\mathbb C)$, that comes equipped with a map that assigns to each prime $\mathfrak {p}\not \in S$ a semisimple conjugacy class $s(\mathfrak {p})$ of $\mathrm {ST}(A)$ for which

$$\begin{aligned} \det (1-s(\mathfrak {p})T)=\overline{L}_\mathfrak {p}(A,T). \end{aligned}$$

Let $\mu$ be the pushforward of the Haar measure of $\mathrm {ST}(A)$ to its set of conjugacy classes X, and let $\{s(\mathfrak {p})\}_\mathfrak {p}$ denote the sequence of conjugacy classes $s(\mathfrak {p})$ arranged in an order compatible with the partial ordering of primes $\mathfrak {p}$ by norm. The generalized Sato–Tate conjecture predicts that:

• (ST) The sequence $\{s(\mathfrak {p})\}_\mathfrak {p}$ is equidistributed on X with respect to the measure $\mu$.

This conjecture has been proved for abelian varieties of dimension one (elliptic curves) over a totally real [15] or CM number field [1], and in several special cases for abelian varieties of higher dimension, including abelian varieties with potential CM [19].

For each $s\in X$, we write $\det (1-sT)=:\sum _{j=0}^{2g} a_jT^j$, and define

$$\begin{aligned} I_j:=\left[ -\left( {\begin{array}{c}2g\\ j\end{array}}\right) ,\left( {\begin{array}{c}2g\\ j\end{array}}\right) \right] \,,\qquad \text {and}\qquad I:=\prod _{j=1}^g I_j. \end{aligned}$$

For $0\le j \le 2g$ we have $a_j\in I_j$ and $a_j=a_{2g-j}$ for $0 \le j\le 2g$, since the eigenvalues of any conjugacy class of $\mathrm {USp}(2g)$ come in complex conjugate pairs on the unit circle. Consider the maps

$$\begin{aligned} \Phi :X {\longrightarrow } I,\qquad \Phi _j:=X {\mathop {\longrightarrow }\limits ^{\Phi }} I {\mathop {\longrightarrow }\limits ^{\varpi _j}} I_j, \end{aligned}$$

where $\Phi$ is defined by $\Phi (s)=(a_1,\dots ,a_g)$ and $\varpi _j$ is the projection to the jth component. Let $\mu _I$ (resp. $\mu _{I_j}$) denote the projection of the measure $\mu$ by the map $\Phi$ (resp. $\Phi _j$). We will call $\mu _I$ the joint coefficient measure and the set of measures $\{\mu _{I_j}\}_j$, the independent coefficient measures.

The measures $\mu _I$ and $\mu _{I_j}$ are, respectively, determined by their moments

$$\begin{aligned} \mathrm {M }_{n_1,\dots ,n_g}[\mu _I]:=\int _I a_1^{n_1}\cdots a_g^{n_g}\mu _I(a_1,\dots ,a_g),\qquad \mathrm {M }_{n}[\mu _{I_j}]:=\int _{I_j} a_j^{n}\mu _{I_j}(a_j), \end{aligned}$$

(1.1)

for $n_1,\dots ,n_g\ge 0$ and $n\ge 0$. We denote by $a_j(A)(\mathfrak {p})$, or simply $a_j(\mathfrak {p})$, the jth coefficient $\Phi _j(s(\mathfrak {p}))$ of the normalized L-polynomial, and by $a(A)(\mathfrak {p})$, or simply $a(\mathfrak {p})$, the g-tuple $\Phi (s(\mathfrak {p}))$ of coefficients of the normalized L-polynomial. We can now consider the following successively weaker versions of the generalized Sato–Tate conjecture:

(ST${}^\prime$):

The sequence $\{a(\mathfrak {p})\}_\mathfrak {p}$ is equidistributed on I with respect to $\mu _I$.

(ST${}^{\prime \prime }$):

The sequences $\{a_j(\mathfrak {p})\}_\mathfrak {p}$ are equidistributed on $I_j$ with respect to $\mu _{I_j}$, for $1\le j \le g$.

Let $\pi (x)$ count the number of primes $\mathfrak {p}\not \in S$ for which $N(\mathfrak {p})\le x$. If we define

$$\begin{aligned} \mathrm {M }_{n_1,\dots ,n_g}[a]{:=}\lim _{x\rightarrow \infty } \frac{1}{\pi (x)}\!\!\sum _{N(\mathfrak {p})\le x}\!\! a_1(\mathfrak {p})^{n_1} \cdots a_g(\mathfrak {p})^{n_g}, \quad \mathrm {M }_n[a_j]{:=}\lim _{x\rightarrow \infty } \frac{1}{\pi (x)}\!\!\sum _{N(\mathfrak {p})\le x}\!\! a_j(\mathfrak {p})^{n},\nonumber \\ \end{aligned}$$

(1.2)

then (ST${}^\prime$) holds if and only if $\mathrm {M }_{n_1,\dots ,n_g}[\mu _I]=\mathrm {M }_{n_1,\dots ,n_g}[a]$ for every $n_1,\dots ,n_g\ge 0$, while (ST${}^{\prime \prime }$) holds if and only if $\mathrm {M }_{n}[\mu _{I_j}]=\mathrm {M }_n[a_j]$ for every $n\ge 0$ and $1\le j\le g$.

Let $A'$ be an abelian variety defined over a number field $k'$ also of dimension g, and let $X'$, $\mu '$, $\mu _I'$, $\mu _{I_j}'$ be the data associated with $A'$ corresponding to X, $\mu$, $\mu _I$, $\mu _{I_j}$, respectively. The following implications are immediate:

$$\begin{aligned} \mathrm {ST}(A)=\mathrm {ST}(A') \quad \Rightarrow \quad \mu _I=\mu _I'\quad \Rightarrow \quad \{\mu _{I_j}\}_j=\{\mu _{I_j}'\}_j. \end{aligned}$$

(1.3)

The classification of Sato–Tate groups of elliptic curves and abelian surfaces together with the explicit computation of their Haar measures implies that for $g\le 2$ the converses of the implications in (1.3) both hold; see [10]. In this article, we show that for $g=3$, there are cases in which the converse of the second implication of (1.3) fails to hold.¹

Main result. In this article, we obtain the counterexamples alluded to in the previous paragraph by searching among abelian threefolds defined over a number field that are ${\overline{\mathbb Q}}$-isogenous to the cube of an elliptic curve with complex multiplication (CM). More precisely, we obtain a complete classification of the Sato–Tate groups, the joint coefficient measures, and the independent coefficient measures of the Jacobians of twists of the Fermat and the Klein quartics (which are both ${\overline{\mathbb Q}}$-isogenous to the cube of a CM elliptic curve). The Fermat and Klein quartics are, respectively, given by the equations

$$\begin{aligned} \tilde{C}^0_1:x^4+y^4+z^4=0, \qquad \tilde{C}^0_7:x^3y+y^3z+z^3x=0, \end{aligned}$$

(1.4)

and they have the two largest automorphism groups among all genus 3 curves, of sizes 96 and 168, respectively. Our main result is summarized in the following theorem.

Theorem 1

The following hold:

• (i) There are 54 distinct Sato–Tate groups of twists of the Fermat quartic. These give rise to 54 (resp. 48) distinct joint (resp. independent) coefficient measures.

• (ii) There are 23 distinct Sato–Tate groups of twists of the Klein quartic. These give rise to 23 (resp. 22) distinct joint (resp. independent) coefficient measures.

• (iii) There are 60 distinct Sato–Tate groups of twists of the Fermat or the Klein quartics. These give rise to 60 (resp. 54) distinct joint (resp. independent) coefficient measures.

One motivation for our work is a desire to extend the classification of Sato–Tate groups that is known for dimensions $g\le 2$ to dimension 3. Of the 52 Sato–Tate groups that arise for abelian surfaces (see [10, Table 10] for a list), 32 can be realized as the Sato–Tate group of the Jacobian of a twist of one of the two genus 2 curves with the largest automorphism groups, as shown in [12]; these groups were the most difficult to treat in [10] and notably include cases missing from the candidate list of trace distributions identified in [21, Table 13]. While the classification of Sato–Tate groups in dimension 3 remains open, the 60 Sato–Tate groups identified in Theorem 1 and explicitly described in Sect. 3.3 are likely to include many of the most delicate cases and represent significant progress toward this goal.

Overview of the paper. This article can be viewed as a genus 3 analog of [12], where the Sato–Tate groups of the Jacobians of twists of the curves $y^2=x^5-x$ and $y^2=x^6+1$ were computed. However, there are two important differences in the techniques we use here; these are highlighted in the paragraphs below that outline our approach. We also note [13], where the Sato–Tate groups of the Jacobians of certain twists of the genus 3 curves $y^2=x^7-x$ and $y^2=x^8+1$ are computed, and [2], where the Sato–Tate groups of the Jacobians of twists of the curve $y^2=x^8-14x^4+1$ are determined. Like the Fermat and Klein quartics we consider here, these three curves represent extremal points in the moduli space of genus 3 curves, but they are all hyperelliptic, and their automorphism groups are smaller (of order 24, 32, 48, respectively).

As noted above, the Sato–Tate conjecture is known for abelian varieties that are ${\overline{\mathbb Q}}$-isogenous to a product of CM abelian varieties [19, Cor. 15]. It follows that we can determine the set of independent coefficient measures $\{\mu _{I_j}\}_j$ by computing the sequences $\{\mathrm {M }_n[a_j]\}_{j,n}$, and similarly for $\mu _I$ and the sequences $\{M_{n_1,\ldots ,n_g}[a]\}_{n_1,\ldots ,n_g}$. Closed formulas for these sequences are determined in Sect. 2 in the more general setting of abelian threefolds defined over a number field k that are ${\overline{\mathbb Q}}$-isogenous to the cube of an elliptic curve defined over k; see Proposition 2.2 and Corollary 2.4. This analysis closely follows the techniques developed in [12, §3].

In Sect. 3, we specialize to the case of Jacobians of twists of the Fermat and Klein quartics. In Sect. 3.2, we obtain a complete list of possibilities for $\{\mathrm {M }_n[a_j]\}_{j,n}$: there are 48 in the Fermat case, 22 in the Klein case, and 54 when combined; see Corollary 3.12. We also compute lower bounds on the number of possibilities for $\{\mathrm {M }_{n_1,n_2,n_3}[a]\}_{n_1,n_2,n_3}$ by computing the number of possibilities for the first several terms (up to a certain conveniently chosen bound) of this sequence. These lower bounds are 54 in the Fermat case, 23 in the Klein case, and 60 when combined; see Proposition 3.13.

The first main difference with [12] arises in Sect. 3.3, where we compute the Sato–Tate groups of the twists of the Fermat and Klein quartics using the results of [3]. Such an analysis would have been redundant in [12], since a complete classification of Sato–Tate groups of abelian surfaces was already available from [10]. We show that there are at most 54 in the Fermat case, and at most 23 in the Klein case; see Corollaries 3.23 and 3.26. Combining the implications in (1.3) together with the lower bounds of Sect. 3.2 and upper bounds of Sect. 3.3 yields Theorem 1.

The second main difference with [12] arises in Sect. 3.4, where we provide explicit equations of twists of the Fermat and Klein quartics that realize each of the possible Sato–Tate groups. Here, the computational search used in [12] is replaced by techniques developed in [22, 23] that involve the resolution of certain Galois embedding problems, and a moduli interpretation of certain twists $X_E(7)$ of the Klein quartic as twists of the modular curve X(7), following [14]. In order to apply the latter approach, which also plays a key role in [25], we obtain a computationally effective description of the minimal field over which the automorphisms of $X_E(7)$ are defined (see Propositions 3.34 and 3.35), a result that may have other applications.

Finally, in Sect. 3.5, we give an algorithm for the efficient computation of the L-polynomials of twists of the Fermat and Klein quartics. This algorithm combines an average polynomial-time for computing Hasse–Witt matrices of smooth plane quartics [18] with a result specific to our setting that allows us to easily derive the full L-polynomial at $\mathfrak {p}$ from the Frobenius trace using the splitting behavior of $\mathfrak {p}$ in certain extensions; see Proposition 3.38. Our theoretical results do not depend on this algorithm, but it played a crucial role in our work by allowing us to check our computations and may be of independent interest.

Notation. Throughout this paper, k denotes a number field contained in a fixed algebraic closure $\overline{\mathbb Q}$ of $\mathbb Q$. All the field extensions of k, we consider are algebraic and assumed to lie in ${\overline{\mathbb Q}}$. We denote by $G_k$ the absolute Galois group $\mathrm {Gal}({\overline{\mathbb Q}}/k)$. For an algebraic variety X defined over k and a field extension L / k, write $X_L$ for the algebraic variety defined over L obtained from X by base change from k to L. For abelian varieties A and B defined over k, we write $A\sim B$ if there is an isogeny from A to B that is defined over k. We use $M^\mathrm {T}$ to denote the transpose of a matrix M. We label the isomorphism class ID$(H)=\langle n, m\rangle$ of a finite group H according to the Small Groups Library [4], in which n is the order of H and m distinguishes the isomorphism class of H from all other isomorphism classes of groups of order n.

2 Equidistribution results for cubes of CM elliptic curves

Let A be an abelian variety over k of dimension 3 such that $A_{\overline{\mathbb Q}}\sim E_{\overline{\mathbb Q}}^3$, where E is an elliptic curve defined over k with complex multiplication (CM) by an imaginary quadratic field M. Let L / k be the minimal extension over which all the homomorphisms from $E_{\overline{\mathbb Q}}$ to $A_{\overline{\mathbb Q}}$ are defined. We note that $kM\subseteq L$, and we have ${\text {Hom}}(E_{\overline{\mathbb Q}},A_{\overline{\mathbb Q}})\simeq {\text {Hom}}(E_{L} ,A_{L} )$ and $A_{L}\, {\sim }\, E_{L} ^3$.

Let $\sigma$ and $\overline{\sigma }$ denote the two embeddings of M into ${\overline{\mathbb Q}}$. Consider

where the tensor product is taken via the embedding $\sigma :M\hookrightarrow {\overline{\mathbb Q}}$. Letting $\mathrm {Gal}(L/kM)$ act trivially on ${\overline{\mathbb Q}}$, it acquires the structure of a $\overline{\mathbb Q}[\mathrm {Gal}(L/kM)]$-module of dimension 3 (resp. 9) over ${\overline{\mathbb Q}}$, and similarly for $\overline{\sigma }$.

Definition 2.1

Let $\theta :=\theta _{M,\sigma }(E,A)$ (resp. $\theta _{M,\sigma }(A)$) denote the representation afforded by the module ${\text {Hom}}(E_{L} ,A_{L} )\otimes _{M,\sigma }{\overline{\mathbb Q}}$ (resp. ${\text {End}}(A_{L} )\otimes _{M,\sigma }{\overline{\mathbb Q}}$), and let us similarly define $\overline{\theta }:=\theta _{M,\overline{\sigma }}(E,A)$ and $\theta _{M,\overline{\sigma }}(A)$. Let $\theta _\mathbb Q:=\theta _\mathbb Q(E,A)$ (resp. $\theta _\mathbb Q(A)$) denote the representation afforded by the $\mathbb Q[\mathrm {Gal}({L} /k)]$-module ${\text {Hom}}(E_{L},A_{L})\otimes \mathbb Q$ (resp. ${\text {End}}(A_L)\otimes \mathbb Q$).

For each $\tau \in \mathrm {Gal}({L} /kM)$, we write

$$\begin{aligned} \det (1-\theta (\tau )T)=1+a_1(\theta )(\tau )T+a_2(\theta )(\tau )T^2+a_3(\theta )(\tau )T^3, \end{aligned}$$

so that $a_1(\theta )=-{\text {Tr}}\theta$ and $a_3(\theta )=-\det (\theta )$.

Fix a subextension F / kM of L / kM, and let S be the set of primes of F for which $A_F$ or $E_F$ has bad reduction. Note that by [27, Thm. 4.1] the set S contains the primes of F ramified in L. For $z\in M$, write $|z|:=\sqrt{\sigma (z)\cdot \overline{\sigma }(z)}$. For $\mathfrak {p}\not \in S$, there exists $\alpha (\mathfrak {p})\in M$, such that $|\alpha (\mathfrak {p})|=N(\mathfrak {p})^{1/2}$ and

$$\begin{aligned} a_1(E_F)(\mathfrak {p})=-\frac{\sigma (\alpha (\mathfrak {p}))+\overline{\sigma }(\alpha (\mathfrak {p}))}{N(\mathfrak {p})^{1/2}}\,. \end{aligned}$$

(2.1)

Proposition 2.2

Let A be an abelian variety of dimension 3 defined over k with $A_L\sim E_L^3$, where E is an elliptic curve defined over k with CM by the imaginary quadratic field M. Suppose that $a_3(\theta )(\tau )$ is rational for every $\tau \in G:=\mathrm {Gal}(L/kM)$. Then, for $i=1,2,3$, the sequence $a_i(A_{kM})$ is equidistributed on $I_i=\left[ -\left( {\begin{array}{c}2g\\ i\end{array}}\right) ,\left( {\begin{array}{c}2g\\ i\end{array}}\right) \right]$ with respect to a measure that is continuous up to a finite number of points and therefore uniquely determined by its moments. For $n\ge 1$, we have $\mathrm {M }_{2n-1}[a_1(A_{kM})]=\mathrm {M }_{2n-1}[a_3(A_{kM})]=0$ and:

$$\begin{aligned} \begin{array}{lll} \mathrm {M }_{2n}[a_1(A_{kM})] &{} = &{}\frac{1}{|G|}\sum _{\tau \in G}|a_1(\theta )(\tau )|^{2n} \left( {\begin{array}{c}2n\\ n\end{array}}\right) ,\\ \mathrm {M }_n[ a_2(A_{kM})] &{} = &{}\frac{1}{|G|}\sum _{\tau \in G}\sum _{i=0}^{n}\left( {\begin{array}{c}n\\ i\end{array}}\right) \left( {\begin{array}{c}2i\\ i\end{array}}\right) |a_2(\theta )(\tau )|^i \left( |a_1(\theta )(\tau )|^2-2\cdot |a_2(\theta )(\tau )|\right) ^{n-i},\\ \mathrm {M }_{2n}[a_3(A_{kM})] &{}= &{} \frac{1}{|G|}\left( \sum _{\tau \in G}\sum _{i=0}^{n}\left( {\begin{array}{c}2n\\ 2i\end{array}}\right) \sum _{j=0}^{2i}\sum _{k=0}^{n-i}\left( {\begin{array}{c}2i\\ j\end{array}}\right) (r_1(\tau )-3)^{2i-j}\right. \\ &{}&{} \,\,\,\,\,\,\,\,\,\,\,\left. \cdot r_2(\tau )^{2n-2i}\left( {\begin{array}{c}n-i\\ k\end{array}}\right) 4^k(-1)^{n-i-k}\left( {\begin{array}{c}2j+2n-2k\\ j+n-k\end{array}}\right) \right) . \end{array} \end{aligned}$$

Here, $r_1(\tau )$ and $r_2(\tau )$ are the real and imaginary parts of $a_3(\theta )(\tau )a_2(\theta )(\tau )\overline{a}_1(\theta )(\tau )$, respectively.

Proof

The proof follows the steps of [12, §3.3]. Define

$$\begin{aligned} V_\sigma (A)=V_\ell (A_{kM})\otimes _{M\otimes \mathbb Q_\ell }{\overline{\mathbb Q}}_\ell , \end{aligned}$$

where the tensor product is taken relative to the map of $\mathbb Q_\ell$-algebras $M\otimes \mathbb Q_\ell \rightarrow {\overline{\mathbb Q}}_\ell$ induced by $\sigma$; similarly define $V_{\overline{\sigma }}(A)$, $V_{\sigma }(E)$, and $V_{\overline{\sigma }}(E)$. We then have isomorphisms of $\overline{\mathbb Q}_\ell [G_{kM}]$-modules

$$\begin{aligned} V_\ell (A_{kM})\simeq V_\sigma (A)\oplus V_{\overline{\sigma }}(A),\qquad V_\ell (E_{kM})\simeq V_\sigma (E)\oplus V_{\overline{\sigma }}(E). \end{aligned}$$

It follows from Theorem 3.1 in [9] that

$$\begin{aligned} V_\sigma (A)\simeq \theta _{M,\sigma }(E,A)\otimes V_\sigma (E),\qquad V_{\overline{\sigma }}(A)\simeq \theta _{M,\overline{\sigma }}(E,A)\otimes V_{\overline{\sigma }}(E). \end{aligned}$$

We thus have an isomorphism of $\overline{\mathbb Q}_\ell [G_{kM}]$-modules

$$\begin{aligned} V_\ell (A_{kM})\simeq \bigl (\theta _{M,\sigma }(E,A)\otimes V_\sigma (E)\bigr )\,\oplus \,\bigl (\theta _{M,\overline{\sigma }}(E,A)\otimes V_{\overline{\sigma }}(E)\bigr ). \end{aligned}$$

(2.2)

For each prime $\mathfrak {p}\not \in S$, let us define

$$\begin{aligned} \alpha _1(\mathfrak {p}):=\frac{\sigma (\alpha (\mathfrak {p}))}{N(\mathfrak {p})^{1/2}},\qquad \overline{\alpha }_1(\mathfrak {p}):=\frac{\overline{\sigma }(\alpha (\mathfrak {p}))}{N(\mathfrak {p})^{1/2}}, \end{aligned}$$

where $\sigma (\alpha (\mathfrak {p}))$, as in equation (2.1), gives the action of ${\text {Frob}}_\mathfrak {p}$ on $V_\sigma (E)$. It follows from (2.2) that

$$\begin{aligned} \begin{array}{l} a_1(A_{kM})(\mathfrak {p})=a_1(\mathfrak {p})\alpha _1(\mathfrak {p})+\overline{a}_1(\mathfrak {p})\overline{\alpha }_1(\mathfrak {p}),\\ a_2(A_{kM})(\mathfrak {p})= a_2(\mathfrak {p}) \alpha _1(\mathfrak {p})^2+\overline{a}_2(\theta )\overline{\alpha }_1(\mathfrak {p})^2+ a_1(\mathfrak {p})\overline{a}_1(\mathfrak {p}) ,\\ a_3(A_{kM})(\mathfrak {p})= a_3(\mathfrak {p})\alpha _1(\mathfrak {p}) ^3+\overline{a}_3(\mathfrak {p})\overline{\alpha }_1(\mathfrak {p})^3+\overline{a}_1(\mathfrak {p})a_2(\mathfrak {p})\alpha _1(\mathfrak {p})+a_1(\mathfrak {p})\overline{a}_2(\mathfrak {p})\overline{\alpha }_1(\mathfrak {p}), \end{array} \end{aligned}$$

(2.3)

where to simplify notation we write $a_i(\mathfrak p):=a_i(\theta )({\text {Frob}}_\mathfrak p)$ and $\overline{a}_i(\mathfrak p):=a_i(\overline{\theta })({\text {Frob}}_\mathfrak p)$. Let $r_1(\mathfrak {p})$ and $r_2(\mathfrak {p})$ denote the real and imaginary parts of $a_3(\mathfrak {p})a_2(\mathfrak {p})\overline{a}_1(\mathfrak {p})$, respectively. We have $a_3(\mathfrak {p})^2=1$, since $a_3(\mathfrak {p})$ is a rational root of unity, and we can rewrite the above expressions as

$$\begin{aligned} \begin{array}{lll} a_1(A_{kM})(\mathfrak {p})&{}=&{}|a_1(\mathfrak {p})|\left( z_1(\mathfrak {p})\alpha _1(\mathfrak {p})+\overline{z}_1(\mathfrak {p})\overline{\alpha }_1(\mathfrak {p})\right) ,\\ a_2(A_{kM})(\mathfrak {p})&{}= &{}|a_2(\mathfrak {p})|\left( z_2(\mathfrak {p})\alpha _1(\mathfrak {p})+\overline{z}_2(\mathfrak {p})\overline{\alpha }_1(\mathfrak {p})\right) ^2-2|a_2(\mathfrak {p})|+|a_1(\mathfrak {p})|^2,\\ a_3(A_{kM})(\mathfrak {p})&{}= &{}a_3(\mathfrak {p})\big (\left( \alpha _1(\mathfrak {p})+\overline{\alpha }_1(\mathfrak {p})\right) ^3+(r_1(\mathfrak {p})-3)\left( \alpha _1(\mathfrak {p})+\overline{\alpha }_1(\mathfrak {p})\right) \\ &{}&{}\pm r_2(\mathfrak {p})\sqrt{4-(\alpha _1(\mathfrak {p})+\overline{\alpha }_1(\mathfrak {p}))^2}\big ), \end{array} \end{aligned}$$

where

$$\begin{aligned} z_1(\mathfrak {p})=\frac{a_1(\mathfrak {p})}{|a_1(\mathfrak {p})|},\quad z_2(\mathfrak {p})=\left( \frac{a_2(\mathfrak {p})}{|a_2(\mathfrak {p})|}\right) ^ {1/2} \in \mathrm {U}(1). \end{aligned}$$

Let $\alpha _1$ denote the sequence $\{\alpha _1(\mathfrak {p}_i)\}_{i\ge 1}$ and, for each conjugacy class c of $\mathrm {Gal}(L/kM)$, let $\alpha _{1,c}$ denote the subsequence of $\alpha _1$ obtained by restricting to primes $\mathfrak {p}$ of $\not \in S$ such that ${\text {Frob}}_\mathfrak {p}=c$. By the translation invariance of the Haar measure and [12, Prop. 3.6], for $z\in \mathrm {U}(1)$ and $i\ge 1$ we have

$$\begin{aligned} \mathrm {M }_i[z\alpha _{1,c}+\overline{z}\, \overline{\alpha }_{1,c}]=\mathrm {M }_i[\alpha _{1,c}+\overline{\alpha }_{1,c}]= {\left\{ \begin{array}{ll} \left( {\begin{array}{c}i\\ i/2\end{array}}\right) &{} \text {if }i\text { is even,}\\ 0 &{} \text {if }i\text { is odd}. \end{array}\right. } \end{aligned}$$

(2.4)

The formulas for $\mathrm {M }_{2n}[a_1(A_{kM})]$, $\mathrm {M }_n[a_2(A_{kM})]$, $\mathrm {M }_{2n}[a_3(A_{kM})]$ follow immediately from (2.4) and the Chebotarev Density Theorem (see [12, Prop. 3.10] for a detailed explanation of a similar calculation).$\square$

Remark 2.3

In the statement of the proposition, we included the hypothesis that $a_3(\theta )$ is rational, which is satisfied for Jacobians of twists of the Fermat and Klein curves (see Section 3.1), because this makes the formulas considerably simpler. This hypothesis is not strictly necessary; one can similarly derive a more general formula without it.

Corollary 2.4

Let A be an abelian variety of dimension 3 defined over k with $A_L \,{\sim }\, E_L^3$, where E is an elliptic curve defined over k with CM by the quadratic imaginary field M, with $k\ne kM$. Suppose that $a_3(\theta )(\tau )$ is rational for $\tau \in G:=\mathrm {Gal}(L/kM)$. Then, for $i=1,2,3$, the sequence $a_i(A_{k})$ is equidistributed on $I_i=\left[ -\left( {\begin{array}{c}2g\\ i\end{array}}\right) ,\left( {\begin{array}{c}2g\\ i\end{array}}\right) \right]$ with respect to a measure that is continuous up to a finite number of points and therefore uniquely determined by its moments. For $n\ge 1$, we have $\mathrm {M }_{2n-1}[a_1(A_{k})]=\mathrm {M }_{2n-1}[a_3(A_{k})]=0$ and:

$$\begin{aligned} \begin{array}{lll} \mathrm {M }_{2n}[ a_1(A_{k})] &{} = &{}\frac{1}{2|G|}\sum _{\tau \in G}|a_1(\theta )(\tau )|^{2n} \left( {\begin{array}{c}2n\\ n\end{array}}\right) ,\\ \mathrm {M }_n[a_2(A_{k})] &{} = &{}\frac{1}{2|G|}\Bigl (\sum _{\tau \in G}\sum _{i=0}^{n}\left( {\begin{array}{c}n\\ i\end{array}}\right) \left( {\begin{array}{c}2i\\ i\end{array}}\right) |a_2(\theta )(\tau )|^i \left( |a_1(\theta )(\tau )|^2-2\cdot |a_2(\theta )(\tau )|\right) ^{n-i}\\ &{} &{} +\ \overline{o}(2)3^n+\overline{o}(4)(-1)^n+\overline{o}(8)+\overline{o}(12)2^ n\Bigr ),\\ \mathrm {M }_{2n}[a_3(A_{k})] &{}= &{} \frac{1}{2|G|}\Bigl (\sum _{\tau \in G}\sum _{i=0}^{n}\left( {\begin{array}{c}2n\\ 2i\end{array}}\right) \sum _{j=0}^{2i}\sum _{k=0}^{n-i}\left( {\begin{array}{c}2i\\ j\end{array}}\right) \cdot (r_1(\tau )-3)^{2i-j}\\ &{}&{} \cdot \ r_2(\tau )^{2n-2i}\left( {\begin{array}{c}n-i\\ k\end{array}}\right) 4^k(-1)^{n-i-k}\left( {\begin{array}{c}2j+2n-2k\\ j+n-k\end{array}}\right) \Bigr ). \end{array} \end{aligned}$$

Here, $\overline{o}(n)$ denotes the number of elements in $\mathrm {Gal}(L/k)$ not in G of order n, and $r_1(\tau )$ and $r_2(\tau )$ are the real and imaginary parts of $a_3(\theta )(\tau )a_2(\theta )(\tau )\overline{a}_1(\theta )(\tau )$, respectively.

Proof

For primes of k that split in kM, we invoke Proposition 2.2. Let N be such that $\tau ^N= 1$ for every $\tau \in \mathrm {Gal}(L/k)\setminus G$ (the present proof shows a posteriori that one can take $N=24$, but for the moment it is enough to know that such an N exists). For primes $\mathfrak {p}$ of k that are inert in kM, we will restrict our analysis to those also satisfy:

• (a) $\mathfrak {p}$ has absolute residue degree 1, that is, $N(\mathfrak {p})=p$ is prime.

• (b) $\mathfrak {p}$ is of good reduction for both A and E.

• (c) $\mathbb Q(\sqrt{p})\cap \mathbb Q(\zeta _{4N})=\mathbb Q$, where $\zeta _{4N}$ is a primitive 4Nth root of unity.

These conditions exclude only a density zero set of primes and thus do not affect the computation of moments.

Now define $D(T,\tau ):=\det (1-\theta _{\mathbb Q}(E,A)(\tau )T)$ for $\tau \in \mathrm {Gal}(L/k)\setminus G$, and let $\mathfrak {p}$ be such that ${\text {Frob}}_\mathfrak {p}=\tau$. In the course of the proof of [12, Cor. 3.12], it is shown that:

• (i) The polynomial $\overline{L}_\mathfrak {p}(A,T)$ divides the Rankin–Selberg polynomial $\overline{L}_\mathfrak {p}(E,\theta _\mathbb Q(E,A),T)$.

• (ii) The roots of $D(T,\tau )$ are quotients of roots of $\overline{L}_\mathfrak {p}(A,T)$ and $\overline{L}_\mathfrak {p}(E,T)$.

Since $\overline{L}_\mathfrak {p}(E,T)=1+T^2$ and the roots of $D(T,\tau )$ are Nth roots of unity, it follows from (i) that the roots of $\overline{L}_\mathfrak {p}(A,T)$ are 4Nth roots of unity. In particular, $a_1(A)(\mathfrak {p})$, $a_2(A)(\mathfrak {p})$, $a_3(A)(\mathfrak {p}) \in \mathbb Z[\zeta _{4N}]$. But (a) implies that

$$\begin{aligned} \sqrt{p} \cdot a_1(A)(\mathfrak {p}) \in \mathbb Z, \qquad p\cdot a_2(A)(\mathfrak {p}) \in \mathbb Z,\qquad p\sqrt{p} \cdot a_3(A)(\mathfrak {p}) \in \mathbb Z, \end{aligned}$$

(2.5)

which combined with (c) implies $a_1(A)(\mathfrak {p})=a_3(A)(\mathfrak {p})=0$. This yields the desired moment formulas for $a_1(A_k)$ and $a_3(A_k)$, leaving only $a_2(A_k)$ to consider.

From (2.5), we see that $\overline{L}(A,T)$ has rational coefficients. Both $\overline{L}_\mathfrak {p}(E,T)$ and $D(T,\tau )$ have integer coefficients, hence so does $\overline{L}_\mathfrak {p}(E,\theta _\mathbb Q(E,A),T)$. Moreover, $\overline{L}_\mathfrak {p}(E,\theta _\mathbb Q(E,A),T)$ is also primitive, which by (i) and Gauss’ Lemma implies that $\overline{L}(A,T)$ has integer coefficients. The Weil bounds then imply (see [20, Prop. 4], for example) that the polynomial $\overline{L}_{\mathfrak {p}}(A,T)$ has the form

$$\begin{aligned} 1+aT^2+aT^4+T^6=:P_a(T), \end{aligned}$$

(2.6)

form some $a\in \{-1,0,1,2,3\}$. To compute the moments of $a_2(A_k)$, it remains only to determine how often each value of a occurs as $\tau$ ranges over G. We have

$$\begin{aligned} \begin{array}{l} P_{-1}(T)=(1-T)^2(1+T)^2(1+T^2),\\ P_{0}(T)=(1+T^2)(1-T^2+T^4),\\ P_{1}(T)=(1+T^2)(1+T^4),\\ P_{2}(T)=(1-T+T^2)(1+T+T^2)(1+T^2),\\ P_{3}(T)=(1+T^2)^3.\\ \end{array} \end{aligned}$$

(2.7)

The integer ${\text {ord}}(\tau )$ is even and then condition (ii) and the specific shape of the $P_a(T)$ imply that the only possible orders of $\tau$ are 2, 4, 6, 8, 12. If ${\text {ord}}(\tau )=2$, then all the roots of $\overline{L}_\mathfrak {p}(E,\theta _\mathbb Q(E,A),T)$ are of order 4. By (i), so are the roots of $P_a(T)$, and (2.7) implies that $a=3$.

If ${\text {ord}}(\tau )=4$, then all the roots of $\overline{L}_\mathfrak {p}(E,\theta _\mathbb Q(E,A),T)$ are of order dividing 4. Thus so are the roots of $P_a(T)$, which leaves the two possibilities $a=-1$ or $a=3$. But (ii) implies that the latter is not possible: if $a=3$, then the roots of $D(T,\tau )$ would all be of order dividing 2 and this contradicts the fact that $\tau$ has order 4. Thus $a=-1$.

If ${\text {ord}}(\tau )=6$, then by (ii) we have $a\not =-1,1,3$ (otherwise the order of $\tau$ would not be divisible by 3). If $a=2$, then again by (ii) the polynomial $D(T,\tau )$ would have a root of order at least 12, which is impossible for ${\text {ord}}(\tau )=6$. Thus $a=0$.

If ${\text {ord}}(\tau )=8$, then $\overline{L}_\mathfrak {p}(E,\theta _\mathbb Q(E,A),T)$ has at least 8 roots of order 8 and thus $P_a(T)$ has at least a root of order 8. Thus $a=1$.

If ${\text {ord}}(\tau )=12$, then by (ii) we have $a\not =-1,1,3$ (otherwise the order of $\tau$ would not be divisible by 3). If $a=0$, then again by (ii) the polynomial $D(T,\tau )$ would only have roots of orders 1, 2, 3 or 6, which is incompatible for ${\text {ord}}(\tau )=12$. Thus, $a=2$.$\square$

3 The Fermat and Klein quartics

The Fermat and the Klein quartics admit models over $\mathbb Q$ given by the equations $\tilde{C}^0_1$ and $\tilde{C}^0_7$ of (1.4), respectively. The Jacobian of $\tilde{C}^0_1$ is $\mathbb Q$-isogenous to the cube of an elliptic curve defined over $\mathbb Q$ (see Proposition 3.1), but this is not true for $\tilde{C}^0_7$, which leads us to choose a different model for the Klein quartic. Let us define $C^0_1:=\tilde{C}^0_1$ and

$$\begin{aligned} C^0_7:x^4+ & {} y^4+z^4+6(xy^3+yz^3+zx^3)-3(x^2y^2+y^2z^2+z^2x^2)\\+ & {} 3xyz(x+y+z)=0. \end{aligned}$$

The model $C^0_7$ is taken from [7, (1.22)], and its Jacobian is $\mathbb Q$-isogenous to the cube of an elliptic curve defined over $\mathbb Q$, as we will prove below. One can explicitly verify that the curve $C^0_7$ is ${\overline{\mathbb Q}}$-isomorphic to the Klein quartic by using (3.3) below to show that

$$\begin{aligned} \text {ID}({\text {Aut}}((C^0_7)_{\mathbb Q(\sqrt{-7})}))=\langle 168, 42\rangle . \end{aligned}$$

One similarly verifies that $C_1^0$ is ${\overline{\mathbb Q}}$-isomorphic to the Fermat quartic by using (3.2) below to show

$$\begin{aligned} \text {ID}({\text {Aut}}((C^0_1)_{\mathbb Q(i)}))\simeq \langle 96,64\rangle . \end{aligned}$$

Let $E^0_1$ and $E^0 _7$ be the elliptic curves over $\mathbb Q$ given by the equations

$$\begin{aligned} E^0_1:y^2z=x^3+xz^2, \qquad E^0_7:y^2z = x^3 - 1715xz^2 + 33614z^3, \end{aligned}$$

(3.1)

with Cremona labels 64a4 and 49a3, respectively. We note that $j(E^0_1)=2^6\cdot 3^3$ and $j(E^0_7)=-3^3\cdot 5^3$, thus $E^0_1$ has CM by the ring of integers of $\mathbb Q(i)$, and $E^0_7$ has CM by the ring of integers of $\mathbb Q(\sqrt{-7})$. For future reference, let us fix some notation. The automorphisms

$$\begin{aligned} {\left\{ \begin{array}{ll} s_1([x:y:z])=[z:x:y],\\ t_1([x:y:z])=[-y:x:z],\\ u_1([x:y:z])=[ix:y:z] \end{array}\right. } \end{aligned}$$

(3.2)

generate ${\text {Aut}}((C^0_1)_{\overline{\mathbb Q}})$, whereas the automorphisms

$$\begin{aligned} {\left\{ \begin{array}{ll} s_7([x:y:z])=[y : z : x],\\ t_7([x:y:z])=[-3x-6y+2z :-6x+2y-3z : 2x-3y-6z],\\ u_7([x:y:z])=[-2x+ay-z : a x-y+(1-a)z :-x+(1-a)y-(1+a)z], \end{array}\right. } \end{aligned}$$

(3.3)

with

$$\begin{aligned} a:=\frac{-1+\sqrt{-7}}{2}=\zeta _7+\zeta _7^2+\zeta _7^4, \end{aligned}$$

generate ${\text {Aut}}((C^0_7)_{\overline{\mathbb Q}})$.

Proposition 3.1

For $d=1$ or 7, the Jacobian of $C^0_d$ is $\mathbb Q$-isogenous to the cube of $E_d^0$.

Proof

For $d=1$, we have a nonconstant map $\varphi _1:C^0_1\rightarrow E^0_1$, given by

$$\begin{aligned} \varphi _1([x: y: z])=[-x^3zy : x^2 z^3: z x y^3]. \end{aligned}$$

Thus there exists an abelian surface B defined over $\mathbb Q$ with ${\text {Jac}}(C^0_1)\sim B\times E^0_1$. Suppose that $E^0_1$ was not a $\mathbb Q$-factor of B. Then, the subgroup $\langle s_1,t_1\rangle \subseteq {\text {Aut}}(C^0_1)$, isomorphic to the symmetric group on 4 letters ${\mathrm {S}_4}$, would inject into $({\text {End}}({\text {Jac}}(C^0_1))\otimes \mathbb C)^\times$. There are two options for this $\mathbb C$-algebra: it is either $\mathrm {GL}_1(\mathbb C)^r$ or $\mathrm {GL}_2(\mathbb C)\times \mathrm {GL}_1(\mathbb C)^ s$, with $r,s\in \mathbb Z_{\ge 0}$. In either case, we reach a contradiction with the fact that ${\mathrm {S}_4}$ has no faithful representations whose irreducible constituents have degrees at most 2. Thus, $E^0_1$ is a $\mathbb Q$-factor of B and ${\text {Jac}}(C_1^0)\sim (E^0_1)^2\times E$, where E is an elliptic curve defined over $\mathbb Q$. Applying the previous argument again shows $E\sim E^0_1$, so ${\text {Jac}}(C_1^0)\sim (E^0_1)^3$.

For $d=7$, we have a nonconstant map $\varphi _7:C^0_7\rightarrow E^0_7$, given by

$$\begin{aligned}&\varphi _7([x:y:z])\\&\quad =\left[ -7(x+y+z)(3x-y-9z) : 2^2\cdot 7^2 (-x^2-3xy-xz+2z^2) : (x+y+z)^2\right] , \end{aligned}$$

thus ${\text {Jac}}(C^0_7)\sim B\times E^0_7$ for some abelian surface B defined over $\mathbb Q$. Since ${\mathrm {S}_4}$ is contained in ${\text {Aut}}((C^0_7)_M)\simeq \mathrm {PSL}_2(\mathbb F_7)$, where $M=\mathbb Q(\sqrt{-7})$, we may reproduce the argument above to show that ${\text {Jac}}(C_7^0)_M\sim (E^0_7)^3_M$. It follows that

$$\begin{aligned} {\text {Jac}}(C_7^0)\sim E \times E'\times E''. \end{aligned}$$

where E, $E'$, and $E''$ are either $E^0_7$ or $E^0_7\otimes \chi$, where $\chi$ is the quadratic character of M. But $E^0_7\otimes \chi \sim E^0_7$, since $E^0_7$ has CM by M, and the result follows.$\square$

Remark 3.2

To simplify notation, for the remainder of this article d is either 1 or 7, and we write $C^0$ for $C^0_ d$, $E^0$ for $E^0_d$, M for $\mathbb Q(\sqrt{-d})$, and s, t, u for $s_d$, $t_d$, $u_d$. When d is not specified, it means we are considering both values of d simultaneously.

3.1 Twists

Let C be a k-twist² of $C^0$, a curve defined over k that is ${\overline{\mathbb Q}}$-isomorphic to $C^0$. The set of k-twists of $C^0$, up to k-isomorphism, is in one-to-one correspondence with $H^1(G_k,{\text {Aut}}(C^0_M))$. Given an isomorphism $\phi :C_{\overline{\mathbb Q}}\overset{\sim }{\rightarrow } C^0_{\overline{\mathbb Q}}$, the 1-cocycle defined by $\xi (\sigma ):=\phi ({}^\sigma \phi )^{-1}$, for $\sigma \in G_k$, is a representative of the cohomology class corresponding to C.

Let K / k (resp. L / k) denote the minimal extension over which all endomorphisms of ${\text {Jac}}(C)_{\overline{\mathbb Q}}$ (resp. all homomorphisms from ${\text {Jac}}(C)_{\overline{\mathbb Q}}$ to $E^0_{\overline{\mathbb Q}}$) are defined. Let $\tilde{K}/k$ (resp. $\tilde{L}/k$) denote the minimal extension over which all automorphisms of $C_{\overline{\mathbb Q}}$ (resp. all isomorphisms from $C_{\overline{\mathbb Q}}$ to $C^0_{\overline{\mathbb Q}}$) are defined.

Lemma 3.3

We have the following inclusions and equalities of fields:

$$\begin{aligned} M\subseteq \tilde{K}=K \subseteq \tilde{L}=L. \end{aligned}$$

Proof

The inclusion $M\subseteq \tilde{K}$ follows from the fact that ${\text {Tr}}(A_u)\in M\setminus \mathbb Q$, where $A_u$ is as in (3.12) and (3.13). From the proof of Proposition 3.1, we know that ${\text {Jac}}(C)_{\tilde{K}}\sim E^3$, where E is an elliptic curve defined over $\tilde{K}$ with CM by M. This implies $K=\tilde{K} M$ and $L=\tilde{L}M$, as in the proof of [12, Lem. 4.2].$\square$

We now associate with $C^0$ a finite group $G^0$ that will play a key role in the rest of the article.

Definition 3.4

Let $G_{C^0}:={\text {Aut}}(C^0_{M})\rtimes \mathrm {Gal}(M/\mathbb Q)$, where $\mathrm {Gal}(M/\mathbb Q)$ acts on ${\text {Aut}}(C^0_{M})$ in the obvious way (coefficient-wise action on rational maps). It is straightforward to verify that

$$\begin{aligned} \text {ID}(G_{C^0_1})=\langle 192, 956\rangle ,\qquad \text {ID}(G_{C^0_7})=\langle 336, 208\rangle . \end{aligned}$$

(3.4)

We remark that $G_{C^0_7}\simeq \mathrm {PGL}(\mathbb F_7)$.

As in [12, §4.2], we have a monomorphism of groups

$$\begin{aligned} \lambda _\phi :\mathrm {Gal}(L/k)=\mathrm {Gal}(\tilde{L}/k)\rightarrow G_{C^0},\qquad \lambda _\phi (\sigma )=(\xi (\sigma ),\pi (\sigma )), \end{aligned}$$

where $\pi :\mathrm {Gal}(L/k)\rightarrow \mathrm {Gal}(M/\mathbb Q)$ is the natural projection (which by Lemma 3.3 is well defined). For each $\alpha \in {\text {Aut}}(C^0_M)$, let $\tilde{\alpha }$ denote its image by the embedding ${\text {Aut}}(C^0_M)\hookrightarrow {\text {End}}((E^0_M)^3)$. The 3-dimensional representation

$$\begin{aligned} \theta _{E^0,C^0}:{\text {Aut}}(C^0_M)\rightarrow {\text {Aut}}_{\overline{\mathbb Q}}( {\text {Hom}}(E^0_M,{\text {Jac}}(C^0_M))\otimes _{M,\sigma }{\overline{\mathbb Q}}), \end{aligned}$$

defined by $\theta _{E^0,C^0}(\alpha )(\psi ):=\tilde{\alpha }\circ \psi$ satisfies

$$\begin{aligned} \theta _{E^0,C^0}\circ {\text {Res}}^{k}_{kM}\lambda _\phi \simeq \theta _{M,\sigma }(E^0,{\text {Jac}}(C)), \end{aligned}$$

(3.5)

where ${\text {Res}}^{k}_{kM}\lambda _\phi$ denotes the restriction of $\lambda _\phi$ from $\mathrm {Gal}(L/k)$ to $\mathrm {Gal}(L/kM)$.

Lemma 3.5

Let C be a twist of $C^0$. Then:

$$\begin{aligned} {\text {Tr}}\theta _{E^0,C^0}={\left\{ \begin{array}{ll} \chi _8 &{}\text { if }C^0=C^0_1 \quad \mathrm{(see\,Table\,3a),}\\ \chi _3 &{}\text { if }C^0=C^0_7 \quad \mathrm{(see\,Table\,3b).} \end{array}\right. } \end{aligned}$$

Proof

In the proof of Lemma 3.18, we will construct an explicit embedding

$$\begin{aligned} {\text {Aut}}(C^0_M)\hookrightarrow {\text {End}}((E^0_M)^3)\otimes \mathbb Q,\qquad \alpha \mapsto \tilde{\alpha }. \end{aligned}$$

Fix the basis $B=\{{\text {id}}\times 0\times 0, 0\times {\text {id}}\times 0,0\times 0\times {\text {id}}\}$ for ${\text {Hom}}(E_M^0,{\text {Jac}}(C_M^0))$. In this basis, with the above embedding the representation $\theta _{E^0,C^0}$ is given by

$$\begin{aligned} \theta _{E^0,C^0}(s)=A_s^{-1},\quad \theta _{E^0,C^0}(t)=A_t^{-1},\quad \theta _{E^0,C^0}(u)=A_u^{-1}, \end{aligned}$$

where $A_s$, $A_t$, and $A_u$ are as in (3.12) and (3.13). The lemma follows.$\square$

Remark 3.6

Observe that since $\det (\theta _{E^0,C^0})$ is a rational character of ${\text {Aut}}(C^0_M)$, by (3.5) so is $a_3(\theta )=\det \theta _{M,\sigma }(E^0,{\text {Jac}}(C))$. Thus, Corollary 2.4 can be used to compute the moments of $a_i({\text {Jac}}(C))$ for $i=1,2,3$.

Proposition 3.7

The fields K and L coincide.³

Proof

Note that L / K is the minimal extension over which an isomorphism between $E^0_{\overline{\mathbb Q}}$ and $E_{\overline{\mathbb Q}}$ is defined. It follows that $L=K(\gamma ^{\nicefrac {1}{n}})$ for some $\gamma \in K$, with $n=4$ for $d=1$ and $n=2$ for $d=7$; see [28, Prop. X.5.4]. In either case, $\mathrm {Gal}(L/K)$ is cyclic of order dividing 4 (note that $\mathbb Q(\zeta _n)\subseteq K$). Suppose that $L\not =K$, let $\omega$ denote the element in $\mathrm {Gal}(L/K)$ of order 2, and write $K^0=L^{\langle \omega \rangle }$. Fix an isomorphism $\psi _1:E^0_L\rightarrow E_L$ and an isogeny $\psi _2:(E_{K^0})^3 \rightarrow {\text {Jac}}(C)_{K^0}$. For $i=1,2,3$, let $\iota _i:E_{K^0}\rightarrow (E_{K^0})^3$ denote the natural injection to the ith factor. Then, $\{\psi _2\circ \iota _i\circ \psi _1\}_{i=1,2,3}$ constitute a basis of the ${\overline{\mathbb Q}}[\mathrm {Gal}(L/M)]$-module ${\text {Hom}}(E^0_L,{\text {Jac}}(C)_L)\otimes _{M,\sigma }{\overline{\mathbb Q}}$. Since ${}^{\omega }\psi _1=-\psi _1$, ${}^{\omega }\psi _2=\psi _2$, and ${}^{\omega }\iota _i=\iota _i$, we have ${{\mathrm{Trace}}}\theta _{M,\sigma }(E^0,{\text {Jac}}(C))(\omega )=-3$. But this contradicts (3.5), because there is no $\alpha$ in ${\text {Aut}}(C^0_M)$ for which ${{\mathrm{Trace}}}\theta _{E^0,C^0}(\alpha )=-3$.$\square$

Remark 3.8

By Proposition 3.7, and the identities (2.3) and (3.5), the independent and joint coefficient measures of ${\text {Jac}}(C)$ depend only on the conjugacy class of $\lambda _\phi (\mathrm {Gal}(K/k))$ in $G_{C^0}$. In Proposition 3.22, we will see that this also applies to the Sato–Tate group of ${\text {Jac}}(C)$. For this reason, henceforth, subgroups $H\subseteq G_{C^0}$ will be considered only up to conjugacy.

Definition 3.9

Let $G_0:={\text {Aut}}(C_M^0)\times \langle 1\rangle \subseteq G_{C^0}$, and for subgroups $H\subseteq G_{C^0}$, let $H_0:=H \cap \mathrm {G}_0$. We may view $H_0$ as a subgroup of ${\text {Aut}}(C_M^0)\simeq G_0$ whenever it is convenient to do so.

Noting that $[G_{C^0}:G_0]=2$, for any subgroup H of $G_{C^0}$ there are two possibilities:

(c$_1$):

$H\subseteq G_0$, in which case $[H:H_0]=1$;

(c$_2$):

$H\not \subseteq G_0$, in which case $[H:H_0]=2$.

Remark 3.10

We make the following observations regarding $H\subseteq G_{C^0}$ and cases (c$_1$) and (c$_2$):

• (i) In Sect. 3.4, we will show that for each subgroup $H\subseteq G_{C^0}$, there is a twist C of $C^0$ such that $H=\lambda _\phi (\mathrm {Gal}(K/k))$. From the definition of $\lambda _\phi$, we must then have $H_0=\lambda _\phi (\mathrm {Gal}(K/kM))$. The case (c$_1$) corresponds to $kM = k$, and the case (c$_2$) corresponds to $k\not = kM$.

• (ii) There are 83 subgroups $H \subseteq G_{C^0_1}$ up to conjugacy, of which 24 correspond to case (c$_1$) and 59 correspond to case (c$_2$). In Table 4 we list the subgroups in case (c$_2$). For any subgroup H in case (c$_1$), there exists a subgroup $H'$ in case (c$_2$) such that $H'_0=H$; thus the subgroups in case (c$_1$) can be recovered from Table 4 by looking at the column for $H_0$.

• (iii) There are 23 subgroups $H \subseteq G_{C^0_7}$ up to conjugacy, of which 12 correspond to case (c$_1$) and  11 correspond to case (c$_2$). For all but 3 exceptional subgroups H in case (c$_1$), there exists a subgroup $H'$ in case (c$_2$) such that $H'_0=H$. In Table 5, we list the subgroups in case (c$_2$) as well as the 3 exceptional subgroups, which appear in rows #3, #8, and #12 of Table 5. As in (ii), the non-exceptional subgroups in case (c$_1$) can be recovered from Table 5 by looking at the column for $H_0$, which for the exceptional groups is equal to H.

• (iv) The subgroups $H\subseteq G_{C^0}$ in Tables 4 and 5 are presented as follows. First, generators of $H_0\subseteq G_0\simeq {\text {Aut}}(C^0_M)$ are given in terms of the generators s, t, u for ${\text {Aut}}(C^0_M)$ listed in (3.2) and (3.3). For the 3 exceptional subgroups of Table 5 we necessarily have $H=H_0$, and for the others, H is identified by listing an element $h\in {\text {Aut}}(C^0_M)$ such that

  $$\begin{aligned} H=H_0\cup H_0\cdot (h,\tau ) \subseteq G_{C^0}, \end{aligned}$$

  (3.6)

  where $\tau$ is the generator of $\mathrm {Gal}(M/\mathbb Q)$.

3.2 Moment sequences

We continue with the notation of Sect. 3.1. If C is a k-twist of $C^0$, we define the joint and independent coefficient moment sequences

$$\begin{aligned} \mathrm {M }_\mathrm{joint}(C):=\{\mathrm {M }_{n_1,n_2,n_3}[a(C)]\}_{n_1,n_2,n_3},\qquad \mathrm {M }_\mathrm{indep}(C):=\{\mathrm {M }_n[a_i(C)]\}_{j,n}, \end{aligned}$$

where a(C) and $a_j(C)$ denote $a({\text {Jac}}(C))$ and $a_j({\text {Jac}}(C))$, respectively, as defined in Sect. 1; recall that these moment sequences are defined by and uniquely determine corresponding measures $\mu _I$ and $\mu _{I_j}$, respectively.

Using Lemma 3.5 and (3.5), we can apply Corollary 2.4 to compute the moments $\mathrm {M }_n[a_j(C)]$ for any n, and as explained in Sect. 3.2.2, it is easy to compute $M_{n_1,n_2,n_3}[a(C)]$ for any particular values of $n_1,n_2,n_3$. Magma scripts [6] to perform these computations are available at [11], which we note depend only on the pairs $(H,H_0)$ (or just $H_0$ when $k=kM$) listed in Tables 4 and 5, and are otherwise independent of the choice of C.

3.2.1 Independent coefficient moment sequences

We now show that for any twist of the Fermat or Klein quartic, each of the independent coefficient moment sequences (and hence the corresponding measures) is determined by the first several moments.

Proposition 3.11

Let C and $C'$ be k-twists of $C^0$. For each $i=1,2,3$ there exists a positive integer $N_i$ such that if

$$\begin{aligned} \mathrm {M }_{n}[a_i(C)]=\mathrm {M }_{n}[a_i(C')] \quad \text {for } 1 \le n \le N_i \end{aligned}$$

then in fact

$$\begin{aligned} \mathrm {M }_{n}[a_i(C)]=\mathrm {M }_{n}[a_i(C')] \quad \text {for all } n \ge 1. \end{aligned}$$

Moreover, one can take $N_1=6$, $N_2=6$, $N_3=10$.

Proof

For the sake of brevity, we assume $k\not =kM$ (the case $k=kM$ is analogous and easier). It follows from Corollary 2.4 that, for $i=1,2,3$, the sequence $\{\mathrm {M }_{n}[a_i(C)]\}_{n\ge 0}$ is determined by $|a_1(C)|$, $|a_2(C)|$, $a_3(C) a_2(C)\bar{a}_1(C)$, and $\bar{o}(2)$, $\bar{o}(4)$, $\bar{o}(8)$ (note that $G_{C_1^0}$ and $G_{C_7^0}$ contain no elements of order 12, so we ignore the $\bar{o}(12)$ term in the formula for $\mathrm {M }_n[a_2(C)]$). We consider the Fermat and Klein cases separately.

For the Fermat case, with the notation for conjugacy classes as in Table 3a, let $x_1$ (resp. $x_2$, $x_3$, $x_4$, $x_5$) denote the proportion of elements in $\mathrm {Gal}(L/k)$ lying in the conjugacy class 1a (resp. $2a \cup 2b \cup 4c \cup 4d$, 3a, $4a \cup 4b$, $8a\cup 8b$); note that by Lemma 3.5, we are interested in the representation with character $\chi _8$ listed in Table 3a, which motivates this partitioning of conjugacy classes.

Let $y_1$ (resp. $y_2$, $y_3$) denote the proportion of elements in $\mathrm {Gal}(L/k)$ which do not lie in $\mathrm {Gal}(L/kM)$ and have order 2 (resp. 4, 8). Applying Corollary 2.4, one finds that for $n\ge 1$ we have

$$\begin{aligned} \mathrm {M }_{2n}[a_1(C)]=x_1\cdot 9^n\left( {\begin{array}{c}2n\\ n\end{array}}\right) +(x_2+x_5)\left( {\begin{array}{c}2n\\ n\end{array}}\right) +x_4(-1)^n\left( {\begin{array}{c}2n\\ n\end{array}}\right) . \end{aligned}$$

(3.7)

Evaluating (3.7) at $n=1,2,3$ yields an invertible linear system in $x_1$, $x_2+x_5$, $x_4$ of dimension 3. The moments $\mathrm {M }_{2n}[a_1(C)]$ for $n=1,2,3$ thus determine $x_1$, $x_2+x_5$, $x_4$ and therefore determine all the $\mathrm {M }_{2n}[a_1(C)]$.

For $\mathrm {M }_n[a_2(C)]$, one similarly obtains an invertible linear system in $x_1$, $x_2+x_5$, $x_4$, $y_1$, $y_2$, $y_3$ of dimension 6, and it follows that the moments $\mathrm {M }_n[a_2(C)]$ for $n\le 6$ determine all the $\mathrm {M }_{n}[a_2(C)]$.

For $\mathrm {M }_{2n}[a_3(C)]$, one obtains an invertible linear system in $x_1$, $x_2$, $x_3$, $x_4$, $x_5$ of dimension 5, and it follows that the moments $\mathrm {M }_{2n}[a_2(C)]$ for $n\le 5$ determine all the $\mathrm {M }_{2n}[a_3(C)]$.

In the Klein case one proceeds analogously. With the notation of Table 3b, let $x_1$ (resp. $x_2$, $x_3$, $x_4$) denote the proportion of elements in $\mathrm {Gal}(L/k)$ lying in the conjugacy class 1a (resp. $2a \cup 4a$, 3a, $7a\cup 7b$), and let $y_1$, $y_2$, $y_3$ be as in the Fermat case. Now $x_1$, $x_2$, $x_4$ determine $\mathrm {M }_n[a_1(C)]$; $x_1$, $x_2$, $x_4$ and $y_1$, $y_2$, $y_3$ determine $\mathrm {M }_{n}[a_2(C)]$; and $x_1$, $x_2$, $x_3$, $x_4$ determine $\mathrm {M }_{n}[a_3(C)]$. These proportions are, as before, determined by the first several moments (never more than are needed in the Fermat case), and the result follows. We spare the reader the lengthy details.$\square$

With Proposition 3.11 in hand we can completely determine the moment sequences $\mathrm {M }_n[a_i(C)]$ that arise among k-twists C of $C^0$ by computing the moments $\mathrm {M }_n[a_i(C)]$ for $n\le N_i$ for the 59 pairs $(H,H_0)$ listed in Table 4 in the case $C^0=C^0_1$, and for the 14 pairs $(H,H_0)$ listed in Table 5 (as described in Remark 3.10). Note that each pair $(H,H_0)$ with $H\ne H_0$ gives rise to two moments sequences $\mathrm {M }_n[a_i(C)]$ for each i, one with $k\ne kM$ and one with $k=kM$.

After doing so, one finds that in fact Proposition 3.11 remains true with $N_2=4$ and $N_3=4$. The value of $N_1$ cannot be improved, but one also finds that the sequences $\mathrm {M }_n[a_2(C)]$ and $\mathrm {M }_n[a_3(C)]$ together determine the sequence $\mathrm {M }_n[a_1(C)]$, and in fact just two well-chosen moments suffice.

Corollary 3.12

There are 48 (resp. 22) independent coefficient measures among twists of $C^0_1$ (resp. $C^0_7$). In total, there are 54 independent coefficient measures among twists C of either $C_1^0$ or $C_7^0$, each of which is uniquely distinguished by the moments $\mathrm {M }_3[a_2(C)]$ and $\mathrm {M }_4[a_3(C)]$.

The moments $\mathrm {M }_3[a_2(C)]$ and $\mathrm {M }_4[a_3(C)]$ correspond to the joint moments $\mathrm {M }_{0,3,0}[a(C)]$ and $\mathrm {M }_{0,0,4}[a(C)]$ whose values are listed in Table 6 for each of the 60 distinct joint coefficient moment measures obtained in the next section (this includes all the independent coefficient measures).

3.2.2 Joint coefficient moments

Instead of giving closed formulas for $\mathrm {M }_{n_1,n_2,n_3}[a(C)]$, analogous to those derived for $\mathrm {M }_n[a_j(C)]$ in Corollary 2.4, let us explain how to compute $\mathrm {M }_{n_1,n_2,n_3}[a(C)]$ for specific values of $n_1,n_2,n_3$ (this will suffice for our purposes). Suppose $k\not = kM$ (the other case is similar). By (2.3), we may naturally regard the quantity

$$\begin{aligned} a_1(C)^{n_1}a_2(C)^{n_2}a_3(C)^{n_3} \end{aligned}$$

(3.8)

as an element of the formal polynomial ring ${\overline{\mathbb Q}}[\alpha _1,\bar{\alpha }_1]/(\alpha _1 \bar{\alpha }_1-1)$. The moment $\mathrm {M }_{n_1,n_2,n_3}[a(C)]$ is simply the constant term of (3.8). For $N\ge 0$ and each pair $(H,H_0)$ in Tables 4 and 5, one can then compute truncated joint moment sequences

$$\begin{aligned} \mathrm {M }_\mathrm{joint}^{\le N}(C):=\{\mathrm {M }_{n_1,n_2,n_3}[a(C)]:n_1,n_2,n_3\ge 0,\ n_1+n_2+n_3\le N\}. \end{aligned}$$

By explicitly computing $\mathrm {M }_\mathrm{joint}^{\le 4}(C)$ for all the pairs $(H,H_0)$ listed in Tables 4 and 5, we obtain the following proposition.

Proposition 3.13

There are at least 54 (resp. 23) joint coefficient measures (and hence Sato–Tate groups) of twists of the Fermat (resp. Klein) quartic, and at least 60 in total. These 60 joint coefficient measures are listed in Table 6, in which each is uniquely distinguished by the three moments $\mathrm {M }_{1,0,1}[a(C)]$, $\mathrm {M }_{0,3,0}[a(C)]$, and $\mathrm {M }_{2,0,2}[a(C)]$.

Computing $\mathrm {M }_\mathrm{joint}^{\le N}(C)$ with $N=5,6,7,8,$ does not increase any of the lower bounds in Proposition 3.13, leading one to believe they are tight. We will prove this in the next section, but an affirmative answer to the following question would make it easy to directly verify such a claim.

Question 3.14

Recall the setting of the first paragraph of Sect. 1. In particular, A is an abelian variety defined over a number field k of dimension $g\ge 1$, and $\mu _I$ is the measure induced on I. By [10, Prop. 3.2] and [10, Rem. 3.3], one expects a finite list of possibilities for the Sato–Tate group of A. One thus expects a finite number of possibilities for the sequence $\{\mathrm {M }_{n_1,\dots ,n_g}[\mu _I]\}_{n_1,\dots ,n_g}$. In particular, one expects that there exists $N_g\ge 1$, depending only on g, such that for any abelian variety $A'$ defined over a number field $k'$, if

$$\begin{aligned} \{\mathrm {M }_{n_1,\dots ,n_g}[\mu _I]\}_{n_1,\dots ,n_g}=\{\mathrm {M }_{n_1,\dots ,n_g}[\mu _I']\}_{n_1,\dots ,n_g} \end{aligned}$$

(3.9)

for all $n_1+\dots +n_g\le N_g$, then (3.9) holds for all $n_1,\dots ,n_g\ge 0$. Is there an explicit and effectively computable upper bound for $N_g$?

Lacking an answer to Question, 3.14, in order to determine the exact number of distinct joint coefficient measures, we take a different approach. In the next section, we will classify the possible Sato–Tate groups of twists of the Fermat and Klein quartics. This classification yields an upper bound that coincides with the lower bound of Proposition 3.13.

Table 6 also lists $z_1=[z_{1,0}]$, $z_2=[z_{2,-1},z_{2,0},z_{2,1},z_{2,2},z_{2,3}]$, and $z_3=[z_{3,0}]$, where $z_{i,j}$ denotes the density of the set of primes $\mathfrak {p}$ for which $a_i(C)(\mathfrak {p})=j$. For these, we record the following lemma.

Lemma 3.15

Let C be a k-twist of $C^0$ and let $H_0:=\lambda _\phi (\mathrm {Gal}(K/kM))$. Then,

$$\begin{aligned} z_1({\text {Jac}}(C))= & {} {\left\{ \begin{array}{ll} \frac{o(3)}{|H_0|} &{} \text { if }M\subseteq k, \\ \frac{1}{2}+\frac{o(3)}{2|H_0|} &{} \text { if }M\not \subseteq k, \end{array}\right. } \qquad z_3({\text {Jac}}(C))={\left\{ \begin{array}{ll} 0 &{} \text { if }M\subseteq k, \\ \frac{1}{2} &{} \text { if }M\not \subseteq k, \end{array}\right. } \\ z_2({\text {Jac}}(C))= & {} {\left\{ \begin{array}{ll} \frac{1}{|H_0|}[0,o(3),0,0,0] &{} \text { if }M\subseteq k, \\ \frac{1}{2|H_0|}[\bar{o}(4),o(3)+\bar{o}(6),\bar{o}(8),0,\bar{o}(2)] &{} \text { if }M\not \subseteq k. \end{array}\right. } \end{aligned}$$

Here, $\bar{o} (n)$ is as in Corollary 2.4 and o(n) denotes the number of elements of order n in $H_0$.

Proof

The formula for $z_1$ is immediate from (2.3) and the study of the polynomial (2.6) in the proof of Corollary 2.4, together from the fact that $\tau \in \mathrm {Gal}(L/k)$ satisfies $a_1(\theta )(\tau )=0$ if and only if $\tau$ has order 3 (as can be seen from Table 3).

The formula for $z_2$ follows from a similar reasoning, once one observes that again $a_2(\theta )(\tau )=0$ if and only if $\tau$ has order 3, and the discussion of the end of Corollary 2.4. Note also that, as $G_{C^0}$ contains no elements of order 12, we have $\bar{o}(12)=0$.

For $z_3$, it suffices to note that $a_3(\tau )$ does not vanish.$\square$

3.3 Sato–Tate groups

In this section, for any twist C of $C^0$, we explicitly construct $\mathrm {ST}({\text {Jac}}(C))$, which to simplify notation we denote by $\mathrm {ST}(C)$. The first step is to compute a (non-canonical) embedding

$$\begin{aligned} \iota :{\text {Aut}}(C^0_M)\rightarrow \mathrm {USp}(6) \end{aligned}$$

(see [24] for a very similar approach). Let $\Omega ^1(E^0_M)$ (resp. $\Omega ^1(C^0_M)$) denote the M-vector space of regular differentials of $E^0_M$ (resp. $C^0_M$). Define

$$\begin{aligned} \iota _1:{\text {Aut}}(C^0_{M})\rightarrow {\text {Aut}}(\Omega ^1(C^0_{M})),\qquad \iota _1(\alpha )=(\alpha ^*)^{-1}, \end{aligned}$$

where $\alpha ^* :\Omega ^1(C^0_{M}) \rightarrow \Omega ^1(C^0_{M})$ is the map induced by $\alpha$.

Remark 3.16

Let $f(X,Y)=0$ be an affine model of the plane quartic $C^0_M$. Then,

$$\begin{aligned} \left\{ W_1:=X\frac{dX}{f_Y},W_2:=Y\frac{dX}{f_Y},W_3:=\frac{dX}{f_Y}\right\} , \end{aligned}$$

(3.10)

with $f_Y=\frac{\partial f}{\partial Y}$, is a basis of the regular differentials $\Omega ^1(C^0_ M)$. If we denote by $\omega _{i}$ the regular differential of the ith copy of $E^0_M$ in $(E^0_M)^3$, then

$$\begin{aligned} \{\omega _1,\,\omega _2,\,\omega _3 \} \end{aligned}$$

(3.11)

is a basis of the regular differentials $\Omega ^1(E^0_M)^3$.

Consider the isomorphism

$$\begin{aligned} \iota _2:{\text {End}}(\Omega ^1(C^0_M))\rightarrow {\text {End}}(\Omega ^1(E^0_M)^3) \end{aligned}$$

induced by the isomorphism $\Omega ^1(C^0_M) \simeq \Omega ^1(E^0_M)^3$ that sends $W_i$ to $\omega _i$.

Fix an isomorphism $[\,]:M\rightarrow {\text {End}}(E^0_M)\otimes \mathbb Q$ such that for any regular differential $\omega \in \Omega ^1(E^0_M)$, one has $[m]^*(\omega )=m\omega$ for every $m\in M$ (see [29, Chap. II, Prop. 1.1]) and then define

$$\begin{aligned} \iota _3:{\text {End}}(\Omega ^1(E^0_M)^3)\rightarrow {\text {End}}((E^0_M)^3)\otimes \mathbb Q,\qquad \iota _3((m_{jk}))=([m_{jk}]), \end{aligned}$$

where $m_{ij}\in M$. Let $f_1=i$ and let $f_7=a$. For $d=1,7$, let $\gamma _d\in H_1((E^0_d)^{{\text {top}}}_{\mathbb C}, \mathbb Q)$ be such that $\{\gamma _d, [f_d]_*\gamma _d\}$ is a symplectic basis of $H_1((E^0_d)^{{\text {top}}}_{\mathbb C}, \mathbb Q)$ with respect to the cup product, and use this basis to obtain an isomorphism

$$\begin{aligned} \Theta _d:{\text {End}}(H_1((E^0_d)^{{\text {top}}}_{\mathbb C}, \mathbb Q))\rightarrow \mathrm {GSp}_2(\mathbb Q). \end{aligned}$$

Then, define

$$\begin{aligned} \iota _4:{\text {End}}((E^0_d)^3_M)\rightarrow \mathrm {GSp}_6(\mathbb Q),\qquad ([m_{jk}])\rightarrow (\Theta _d([m_{jk}]_*)). \end{aligned}$$

Finally, define the matrices

$$\begin{aligned} I_2=\begin{pmatrix} 1 &{} 0\\ 0&{}1 \end{pmatrix} ,\qquad J_2=\begin{pmatrix} 0 &{} -1\\ 1 &{} 0 \end{pmatrix},\qquad K_2=\begin{pmatrix} 0 &{} -2\\ 1 &{} -1 \end{pmatrix}. \end{aligned}$$

Remark 3.17

From now on, we fix the following notation: denote by $A_3$ the 3-diagonal embedding of a subset A of $\mathrm {GL}_2$ in $\mathrm {GL}_6$. Throughout this section, we consider the general symplectic group $\mathrm {GSp}_6/\mathbb Q$, the symplectic group $\mathrm {Sp}_6/\mathbb Q$, and the unitary symplectic group $\mathrm {USp}(6)$ with respect to the symplectic form given by the 3-diagonal embedding $(J_2)_3$.

Lemma 3.18

The map

$$\begin{aligned} \iota :{\text {Aut}}(C^0_M)\hookrightarrow ^{\iota _1} {\text {End}}(\Omega ^1(C^0_M))\simeq ^{\iota _2}{\text {End}}(\Omega ^1(E^0_M)^3 )\simeq ^{\iota _3}{\text {End}}((E^0_M)^3)\otimes \mathbb Q\hookrightarrow ^{\iota _4}\mathrm {GSp}_6(\mathbb Q) \end{aligned}$$

is a monomorphism of groups that for $C^0=C^0_1$ is explicitly given by

$$\begin{aligned} \iota (s_1)=\begin{pmatrix} 0 &{} 0 &{} I_2\\ I_2 &{} 0 &{} 0\\ 0 &{} I_2 &{} 0 \end{pmatrix} ,\quad \iota (t_1)=\begin{pmatrix} 0 &{} -I_2 &{} 0\\ I_2 &{} 0 &{} 0\\ 0 &{} 0 &{} I_2 \end{pmatrix} ,\quad \iota (u_1)=\begin{pmatrix} -I_2 &{} 0 &{} 0\\ 0 &{} -J_2 &{} 0\\ 0 &{} 0 &{} -J_2 \end{pmatrix} , \end{aligned}$$

and for $C^0=C^0_7$ is explicitly given by $\iota (s_7)=\iota (s_1)^{\mathrm {T}}$ and

$$\begin{aligned} \iota (t_7)=\frac{1}{7}\begin{pmatrix} -3I_2 &{} -6I_2 &{} 2I_2\\ -6I_2 &{} 2I_2 &{} -3I_2\\ 2I_2 &{} -3I_2 &{} -6I_2 \end{pmatrix} ,\,\,\, \iota (u_7)=\frac{1}{7}\begin{pmatrix} -2I_2-4K_2 &{} 3I_2-K_2 &{} -I_2-2K_2\\ 3I_2-K_2 &{} -I_2-2K_2 &{} -2I_2+3K_2\\ -I_2-2K_2 &{} -2I_2+3K_2 &{} -4I_2-K_2 \end{pmatrix} . \end{aligned}$$

Proof

We first consider the case $C^0=C^0_1$. In the basis of (3.10), the elements $s_1^*$, $t_1^*$, and $u_1^*$ of ${\text {End}}(\Omega ^1(C^0_M))$ are given by the matrices

$$\begin{aligned} A_{s_1}=\begin{pmatrix} 0 &{} 1 &{} 0\\ 0 &{} 0 &{}1\\ 1 &{} 0 &{} 0 \end{pmatrix} ,\,\,\, A_{t_1}=\begin{pmatrix} 0 &{} 1 &{} 0\\ -1 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 \end{pmatrix} ,\,\,\, A_{u_1}=\begin{pmatrix} -1 &{} 0 &{} 0\\ 0 &{} i &{} 0\\ 0 &{} 0 &{} i \end{pmatrix} . \end{aligned}$$

(3.12)

Thus, in the basis of (3.11), the elements $\iota _2\iota _1(s_1)$, $\iota _2\iota _1(t_1)$, $\iota _2\iota _1(u_1)$ of ${\text {End}}(\Omega ^1(E^0_M)^3)$ are given by the matrices $A_{s_1}^{-1}$, $A_{t_1}^{-1}$, $A_{u_1}^{-1}$. It is then enough to check that in the basis $\{\gamma _1,[i]_*\gamma _1\}$ we have $\Theta _1(1)=I_2$ and $\Theta _1(i)=J_2$.

We now assume $C^0=C^0_7$. In the basis of (3.10), the matrices associated with $s_7^*$, $t_7^*$, $u_7^*$ are:

$$\begin{aligned} A_{s_7}=\begin{pmatrix} 0 &{} 0 &{} 1\\ 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 \end{pmatrix}, \,\,\, A_{t_7}=\frac{1}{7}\begin{pmatrix} -3 &{} -6 &{} 2\\ -6 &{} 2 &{} -3\\ 2 &{} -3 &{}-6 \end{pmatrix}, \,\,\, A_{u_7}=\frac{1}{7}\begin{pmatrix} 2+4a &{} 4+a &{} 1+2a\\ 4+a &{} 1+2a &{} -5-3a\\ 1+2a &{} -5-3a &{} -3+a \end{pmatrix}. \end{aligned}$$

(3.13)

Thus, in the basis of (3.10), the elements $\iota _2\iota _1(s_7)$, $\iota _2\iota _1(t_7)$, $\iota _2\iota _1(u_7)$ of ${\text {End}}(\Omega ^1_M(E^0_7)^3)$ are given by the matrices $A_{s_7}^{-1}$, $A_{t_7}^{-1}$, $A_{u_7}^{-1}$. It is then enough to check that in the basis $\{\gamma _7,[a]_*\gamma _7\}$ we have $\Theta _7(1)=I_2$ and $\Theta _7(a)=K_2$. But this is clear, since

$$\begin{aligned} \begin{array}{l} {[}a]_{*}(\gamma _{7})=0\cdot \gamma _{7}+1\cdot ([a]_{*}\gamma _7),\\ {[}a]_{*}([a]_{*}\gamma _7)=[a^2]_{*}\gamma _{7}=[-a-2]_{*}\gamma _{7}=-2\cdot \gamma _{7}-1\cdot ([a]_{*}\gamma _7), \end{array} \end{aligned}$$

and this completes the proof.$\square$

Remark 3.19

Note that since ${\text {Aut}}(C^0_M)$ has finite order, the image of $\iota$ is contained in $\mathrm {USp}_6(\mathbb Q)$.

Remark 3.20

It is easy to check that the matrices $\iota (s_1)$, $\iota (t_1)$, $\iota (u_1)$ (resp. $\iota (s_7)$, $\iota (t_7)$, $\iota (u_7)$) are symplectic with respect to $J:=(J_2)_3$.

The following theorem gives an explicit description of the Sato–Tate group of a twist of the Fermat or Klein quartic corresponding to a subgroup H of the group

$$\begin{aligned} G_{C_0}:={\text {Aut}}(C^0_M)\times \mathrm {Gal}(M/\mathbb Q) \end{aligned}$$

associated with $C^0$ (see Definition 3.4).

Theorem 3.21

The following hold:

• (i) The monomorphism of Lemma 3.18 extends to a monomorphism

  $$\begin{aligned} \iota :G_{C^0}\hookrightarrow \mathrm {USp}(6)/\langle -1\rangle \, \end{aligned}$$

  by defining

  $$\begin{aligned} \iota ((1,\tau )):={\left\{ \begin{array}{ll} \frac{1}{\sqrt{2}} \begin{pmatrix} i &{} i\\ i &{} -i \end{pmatrix}_3 &{} \text { if } C^0=C^0_1,\\ \begin{pmatrix} i &{} -i\\ 0 &{} -i \end{pmatrix}_3&\text { if } C^0=C^0_7, \end{array}\right. } \end{aligned}$$

  where $\tau$ denotes the non-trivial element of $\mathrm {Gal}(M/\mathbb Q)$.

• (ii) Let $\phi :C_{\overline{\mathbb Q}}\rightarrow C^ 0_{\overline{\mathbb Q}}$ denote a k-twist of $C^0$ and write $H:=\lambda _\phi (\mathrm {Gal}(K/k))\subseteq G_{C^0}$. The Sato–Tate group of ${\text {Jac}}(C)$ is given by

  $$\begin{aligned} \mathrm {ST}(C)=\mathrm {ST}(E^0,1)_3\cdot \iota (H), \end{aligned}$$

  where

  $$\begin{aligned} \mathrm {ST}(E^0,1)=&\left\{ \begin{pmatrix} \cos (2\pi r) &{} \sin (2\pi r)\\ -\sin (2\pi r) &{} \cos (2\pi r) \end{pmatrix}\,|\, r\in [0,1] \right\} \, \end{aligned}$$

  if $C^0=C^0_1$, and

  $$\begin{aligned} \mathrm {ST}(E^0,1)= \left\{ \begin{pmatrix} \cos (2\pi r)-\frac{1}{\sqrt{7}}\sin (2\pi r) &{} \frac{4}{\sqrt{7}}\sin (2\pi r) \\ -\frac{2}{\sqrt{7}} \sin (2\pi r) &{} \cos (2\pi r)+\frac{1}{\sqrt{7}}\sin (2\pi r) \end{pmatrix}\,|\,r\in [0,1] \right\} \end{aligned}$$

  if $C^0=C^0_7$.

Proof

To prove (i) it is enough to note that $\iota ((1,\tau ))^2=1$ in $\mathrm {USp}(6)/\langle -1\rangle$ and that $\iota ((1,\tau ))$ acts by matrix conjugation on $\iota ({\text {Aut}}(C^0_M))$ as $\tau$ acts by Galois conjugation on ${\text {Aut}}(C^0_M)$. If $C^0= C^0_1$ (resp. $C^0=C^0_7$), the latter is equivalent to

$$\begin{aligned} \iota ((1,\tau ))^{-1} J_2\iota ((1,\tau ))= -J_2,\qquad \big (\, \text {resp. }\iota ((1,\tau ))^{-1} K_2\iota ((1,\tau ))= -I_2-K_2 \,\big ), \end{aligned}$$

which is straightforward to check.

For (ii), we consider only the case $kM\ne k$, since the case $k=kM$ can be easily deduced from the case $kM\ne k$. Recall from [3] that $\mathrm {ST}(E^0)$ is a maximal compact subgroup of the algebraic Sato–Tate group ${\text {AST}}(E^0)\otimes \mathbb C$ attached to $E^0$. Recall that we have ${\text {AST}}(E^0)={\text {L}}(E^0,1)\cup {\text {L}}(E^0,\tau )$, where for $\sigma \in \mathrm {Gal}(kM/k)$ one has

$$\begin{aligned} {\text {L}}(E^0,\sigma ) :=\{\gamma \in \mathrm {Sp}_{2}\,|\,\gamma ^{-1} \alpha \gamma = {}^\sigma \alpha \text{ for } \text{ all } \alpha \in {\text {End}}(E^0_{\overline{\mathbb Q}})\otimes {\mathbb Q}\}. \end{aligned}$$

(3.14)

This induces a decomposition $\mathrm {ST}(E^0)=\mathrm {ST}(E^0,1)\cup \mathrm {ST}(E^0,\tau )$ that can be explicitly determined.

For the case $C^0=C^0_1$, we have

$$\begin{aligned} {\text {L}}(E^0,1)(\mathbb C)&=\{A\in M_2(\mathbb C)|A^\mathrm {T}J_2A=J_2,\, A^{-1}J_2A=J_2 \} \\&=\left\{ \begin{pmatrix} c &{} b \\ -b &{} c \end{pmatrix}\,|\,c,b\in \mathbb C,\,c^2+b^2=1 \right\} . \end{aligned}$$

Thus, a maximal compact subgroup of ${\text {L}}(E^0,1)(\mathbb C)$ is

$$\begin{aligned} \mathrm {ST}(E^0,1) =\left\{ \begin{pmatrix} \cos (2\pi r) &{} \sin (2\pi r) \\ - \sin (2\pi r) &{} \cos (2\pi r) \end{pmatrix}\,|\,r\in [0,1] \right\} . \end{aligned}$$

Analogously,

$$\begin{aligned} {\text {L}}(E^0,\tau )(\mathbb C)&=\{A\in M_2(\mathbb C)|A^\mathrm {T}J_2A=J_2,\, A^{-1}J_2A=-J_2 \} \\&=\left\{ \begin{pmatrix} ic &{} ib \\ ib &{}-i c \end{pmatrix}\,|\,c,b\in \mathbb C,\,c^2+b^2=1 \right\} . \end{aligned}$$

Thus, a maximal compact subgroup of ${\text {L}}(E^0,\tau )(\mathbb C)$ is

$$\begin{aligned} \mathrm {ST}(E^0,\tau ) =\mathrm {ST}(E^0,1)\cdot \frac{1}{\sqrt{2}} \begin{pmatrix} i &{} i \\ i &{}-i \end{pmatrix} . \end{aligned}$$

(3.15)

There is a relation between the algebraic Sato–Tate groups ${\text {AST}}(C)$ and ${\text {AST}}(C^0)$ attached to ${\text {Jac}}(C)$ and ${\text {Jac}}(C^0)$, respectively, given by [12, Lemma 2.3]. If we put $H_0:=\lambda _\phi (\mathrm {Gal}(K/kM))$, this relation implies that

$$\begin{aligned} {\text {AST}}(C)={\text {L}}(E^0,1)_3\cdot \iota (H_0)\cup {\text {L}}(E^0,\tau )_3\cdot \iota ((1,\tau )^{-1}(H\setminus H_0)). \end{aligned}$$

Then, (3.15) implies

$$\begin{aligned} \mathrm {ST}(C)=\mathrm {ST}(E^0,1)_3\big (\iota (H_0) \cup \iota (H\setminus H_0)\big )=\mathrm {ST}(E^0,1)_3\cdot \iota (H). \end{aligned}$$

(3.16)

Note that, even if $\iota (H)$ is only defined as an element of $\mathrm {USp}(6)/\langle -1\rangle$, the product $\mathrm {ST}(E^0,1)_3\cdot \iota (H)$ is well defined inside $\mathrm {USp}(6)$, provided that $-1\in \mathrm {ST}(E^0,1)_3$.

For the case $C^0=C^0_7$, we have

$$\begin{aligned} {\text {L}}(E^0,1)(\mathbb C)&= \{A\in M_2(\mathbb C)|A^{\mathrm {T}} J_{2}A=J_{2},\, A^{-1}K_{2}A=K_{2}\} \\&=\left\{ \begin{pmatrix} c-b &{} 4b \\ -2b &{} c+b \end{pmatrix}\,|\,c,b\in \mathbb C,\,c^2+7b^2=1 \right\} . \end{aligned}$$

Thus, a maximal compact subgroup of ${\text {L}}(E^0,1)(\mathbb C)$ is

$$\begin{aligned} \mathrm {ST}(E^0,1) =\left\{ \begin{pmatrix} \cos (2\pi r)-\frac{1}{\sqrt{7}}\sin (2\pi r) &{} \frac{4}{\sqrt{7}}\sin (2\pi r) \\ -\frac{2}{\sqrt{7}} \sin (2\pi r) &{} \cos (2\pi r)+\frac{1}{\sqrt{7}}\sin (2\pi r) \end{pmatrix}\,|\,r\in [0,1] \right\} . \end{aligned}$$

Analogously,

$$\begin{aligned} \mathrm {ST}(E^0,\tau )&=\{A\in M_2(\mathbb C)|A^\mathrm {T}J_2A=J_2,\, A^{-1}K_2A=-I_2-K_2 \} \\&=\left\{ \begin{pmatrix} ic-ib &{} 4ib \\ \frac{ic}{2}+\frac{3ib}{2} &{} ib-ic \end{pmatrix}\,|\,c,b\in \mathbb C,\,c^2+7b^2=1 \right\} . \end{aligned}$$

Thus, a maximal compact subgroup of ${\text {L}}(E^0,\tau )(\mathbb C)$ is

$$\begin{aligned} \mathrm {ST}(E^0,\tau ) =\mathrm {ST}(E^0,1)\cdot \begin{pmatrix} i &{} -i \\ 0 &{}-i \end{pmatrix} . \end{aligned}$$

We can now apply [12, Lemma 2.3] exactly as in the case $C^0=C^0_1$ to complete the proof.

$\square$

The previous theorem describes the Sato–Tate group of a twist C of $C^0$. Now suppose that C and $C'$ are both twists of $C^0$. The next proposition gives an effective criterion to determine when $\mathrm {ST}(C)$ and $\mathrm {ST}(C')$ coincide. Let $H\subseteq G_{C^0}$ (resp. $H'$) be attached to C (resp. $C'$) as in Remark 3.10.

Proposition 3.22

If H and $H'$ are conjugate in $G_{C^0}$, then $\mathrm {ST}(C)$ and $\mathrm {ST}(C')$ coincide.

Proof

Since the Sato–Tate group is defined only up to conjugacy, is suffices to exhibit $A\in \mathrm {GL}_6(\mathbb C)$ such that $A^{-1}\mathrm {ST}(C)A=\mathrm {ST}(C')$. Let $g\in G_{C^0}$ be such that $H'=g^{-1}H g$. It is straightforward to check that $\iota (G_{C^0})$ normalizes the group $\mathrm {ST}(E^0,1)_3$. In particular, by Theorem 3.21 (ii), we have

$$\begin{aligned} \mathrm {ST}(C')=\mathrm {ST}(E^0,1)_3\iota (H')=\iota (g)^{-1}\mathrm {ST}(E^0,1)_3\iota (H)\iota (g)=\iota (g)^{-1}\mathrm {ST}(C)\iota (g). \end{aligned}$$

(3.17)

$\square$

Corollary 3.23

There are at most 23 Sato–Tate groups of twists of the Klein quartic $C_7^0$.

Proof

There are 23 subgroups of $G_{C^0_7}$, up to conjugacy.$\square$

In the Fermat case, $\mathrm {ST}(C)$ and $\mathrm {ST}(C')$ may coincide when H and $H'$ are not conjugate in $G_{C^0}$. We thus require a sharper criterion.

Definition 3.24

Let C and $C'$ be twists of $C^0$ and $C^{0\prime }$, respectively (here $C^0$ and $C^{0\prime }$ both denote one of $C^0_1$ or $C^0_7$, but possibly not the same curve in both cases), and let H and $H'$ be the corresponding attached groups. We say that H and $H'$ are equivalent if there exists an isomorphism

$$\begin{aligned} \Psi :H \rightarrow H' \end{aligned}$$

(3.18)

such that $\Psi (H_0)=H_0'$ and for every $h \in H_0$, we have

$$\begin{aligned} {\text {Tr}}(j(h))= {\text {Tr}}(j(\Psi (h))), \end{aligned}$$

(3.19)

where $H_0$ and $H_0'$ are defined as in Definition 3.9 and j denotes compositions $\iota _2\circ \iota _1$ of the embeddings defined in Lemma 3.18 for $C^0$ and $C^{0\prime }$ (two different maps j if $C^0\ne C^{0\prime }$).

Proposition 3.25

Let C and $C'$ be twists of $C^0$ and $C^{0\prime }$. If H and $H'$ are equivalent, then $\mathrm {ST}(C)$ and $\mathrm {ST}(C')$ coincide.

Proof

Let us first assume that $C^0=C^{0\prime }$. By Theorem 3.21 (ii), we can consider the group isomorphism

$$\begin{aligned} \Phi :\mathrm {ST}(C)=\mathrm {ST}(E^0,1)_3\cdot \iota (H)\simeq \mathrm {ST}(C')=\mathrm {ST}(E^0,1)_3\cdot \iota (H') \end{aligned}$$

defined by sending an element of the form $g=g_0\iota (h)$ to $g_0\iota (\Psi (h))$. We aim to show that $\mathrm {ST}(C)$ and $\mathrm {ST}(C')$ are conjugate inside $\mathrm {GL}_6(\mathbb C)$. This amounts to showing that $\mathrm {ST}(C)$ and $\mathrm {ST}(C')$ are equivalent representations of the same abstract group, for which it suffices to prove the following claim: for every $g\in \mathrm {ST}(C)$, we have ${\text {Tr}}(g)={\text {Tr}}(\Phi (g))$. To prove the claim distinguish the cases: (a) $h\in H_0$, and (b) $h\in H\setminus H_0$.

Suppose we are in case (a). By (3.19), there exists $A\in \mathrm {GL}_3(M)$ such that we have $Aj(h)A^{-1}=j(\Psi (h))$ for every $h\in H_0$. Moreover, if we let r denote the composition $\iota _4\circ \iota _3$ of the embeddings defined in Lemma 3.18, the fact that A has entries in M easily implies that r(A) centralizes $\mathrm {ST}(E^0,1)$, and thus we have

$$\begin{aligned} \Phi (g)=g_0r(A)\iota (h) r(A)^{-1}=r(A)g_0\iota (h) r(A)^{-1}=r(A)gr(A)^{-1}, \end{aligned}$$

from which the claim follows. In case (b), we have that both g and $\Phi (g)$ have trace 0, as follows for example from the proof of Corollary 2.4 and the Chebotarev Density Theorem. The claim follows immediately.

If $C^0\ne C^{0\prime }$, then we may assume without loss of generality that C is a twist of $C^0_7$ and $C'$ is a twist of $C^0_1$. Now consider the isomorphism

$$\begin{aligned} \Phi :\mathrm {ST}(C)=\mathrm {ST}(E^0_7,1)_3\cdot \iota (H)\simeq \mathrm {ST}(C')=\mathrm {ST}(E^0_1,1)_3\cdot \iota (H') \end{aligned}$$

defined by sending an element of the form $g=g_0\iota (h)$ to $Tg_0T^{-1}\iota (\Psi (h))$, where

$$\begin{aligned} T=\begin{pmatrix} 1 &{} 0\\ -1/\sqrt{7} &{} 4/\sqrt{7} \end{pmatrix}. \end{aligned}$$

We now note that $T\mathrm {ST}(E^0_1,1) T^{-1}=\mathrm {ST}(E^0_7,1)$, and the proof then proceeds exactly as above; the hypothesis $C^0\not =C^{0\prime }$ implies that we have

$$\begin{aligned} {\text {Tr}}(j(h))={\text {Tr}}(j(\Psi (h)))\in \mathbb Q(\sqrt{-1})\cap \mathbb Q(\sqrt{-7})=\mathbb Q\end{aligned}$$

for every $h\in H_0$, and thus the matrix A from above can be taken in $\mathrm {GL}_3(\mathbb Q)$.

$\square$

Corollary 3.26

The following hold:

• (i) There are at most 54 distinct Sato–Tate groups of twists of the Fermat quartic.

• (ii) There are at most 60 distinct Sato–Tate groups of twists of the Fermat and Klein quartics.

Proof

Determining whether two subgroups H and $H'$ are equivalent is a finite problem. Using the computer algebra program [6], one can determine a set of representatives for equivalence classes of subgroups H that turn out to have size 54 in case (i), and of size 60 in case (ii). For the benefit of the reader, here we give a direct proof of (ii), assuming (i).

The 6 Sato–Tate groups of a twist of the Klein quartic that do not show up as the Sato–Tate group of a twist of the Fermat quartic are precisely those ruled out by the fact that $H_0$ contains an element of order 7 (those in rows #10, #13, #14 of Table 5), since 7 does not divide $\#G_{C_1^0}$.

To show that the other 17 Sato–Tate groups of twists of the Klein quartic also arise for twists of the Fermat quartic, we proceed as follows. Let $H\subseteq G_{C^0_7}$ correspond to a twist C of $C^0_7$ such that $H_0$ does not contain an element of order 7, and let $H'\subseteq C^0_1$ correspond to a twist $C'$ of $C^0_1$. In this case, from Table 3a, b, to ensure that H and $H'$ are equivalent it suffices to check that:

• (1) There exists an isomorphism $\Psi :H\rightarrow H'$ such that $\Psi (H_0)=H_0'$;

• (2) ${\text {Tr}}(j(h))=1$ for every $h\in H_0'$ such that ${\text {ord}}(h)=4$.

From Tables 4 and 5, it is trivial to check that for every H as above, one can always find a subgroup $H'$ such that condition (1) is satisfied. Condition (2) is vacuous except for rows #6, #7, #11, and #12 of Table 5. In these cases, a subgroup $H'$ for which condition (2) is also satisfied can be found by noting that both $j(t_1)$ and $j(t_1^3u_1t_1u_1^3)$ have trace 1. More precisely, one finds that the Sato–Tate groups corresponding to these cases coincide with the Sato–Tate groups of rows #13, #20, #34, and #55 of Table 4, respectively.$\square$

Combining the lower and upper bounds proved in this section yields our main theorem, which we restate for convenience.

Theorem 1

The following hold:

• (i) There are 54 distinct Sato–Tate groups of twists of the Fermat quartic. These give rise to 54 (resp. 48) distinct joint (resp. independent) coefficient measures.

• (ii) There are 23 distinct Sato–Tate groups of twists of the Klein quartic. These give rise to 23 (resp. 22) distinct joint (resp. independent) coefficient measures.

• (iii) There are 60 distinct Sato–Tate groups of twists of the Fermat or the Klein quartics. These give rise to 60 (resp. 54) distinct joint (resp. independent) coefficient measures.

Proof

This follows immediately from Corollaries 3.12, 3.23, 3.26, and Proposition 3.13.$\square$

Corollary 3.27

If C and $C'$ are twists of $C^0$ corresponding to H and $H'$, respectively, then $\mathrm {ST}(C)$ and $\mathrm {ST}(C')$ coincide if and only if H and $H'$ are equivalent.

Remark 3.28

One could have obtained the lower bounds of Proposition 3.13 by computing the joint coefficient measures $\mu _I$ of the Sato–Tate groups explicitly described in Theorem 3.21. This is a lengthy but feasible task that we will not inflict on the reader. We note that this procedure also allows for case-by-case verifications of the equalities $\mathrm {M }_{n_1,n_2,n_3}[\mu _I]=\mathrm {M }_{n_1,n_2,n_3}[a]$ and thus of the Sato–Tate conjecture in the cases considered.

Remark 3.29

Let $\mathfrak X_d$ denote the set of Sato–Tate groups of twists of $C^0_d$. Theorem 3.21 gives a map from the set of subgroups of $G_{C^0_d}$ to $\mathfrak {X}_d$ that assigns to a subgroup $H\subseteq G_{C^0}$ the Sato–Tate group $\mathrm {ST}(E^0,1)_3\cdot \iota (H)$. It also shows that $\mathfrak X_d$ is endowed with a lattice structure compatible with this map and the lattice structure on the set of subgroups of $G_{C^0_d}$. Moreover, Proposition 3.22 says that this map factors via

$$\begin{aligned} \varepsilon _d :\mathfrak C_d \rightarrow \mathfrak X_d, \end{aligned}$$

where $\mathfrak C_d$ denotes the lattice of subgroups of $G_{C^0_d}$ up to conjugation. Parts (i) and (ii) of Theorem 1 imply that while the map $\varepsilon _7$ is a lattice isomorphism, the map $\varepsilon _1$ is far from being injective. Corollary 3.27 can now be reformulated by saying that two subgroups $H,\,H'\in \mathfrak C_1$ lie in the same fiber of $\varepsilon _1$ if and only if they are equivalent.

In virtue of the above remark, one might ask about conditions on twists C and $C'$ corresponding to distinct but equivalent groups H and $H'$ that ensure their Jacobians have the same Sato–Tate group. One such condition is that ${\text {Jac}}(C)$ and ${\text {Jac}}(C')$ are isogenous (recall that the Sato–Tate group of an abelian variety is an isogeny invariant). The next proposition shows that, under the additional hypothesis that K and $K'$ coincide, the previous statement admits a converse.

Proposition 3.30

Let C and $C'$ be k-twists of $C^0$. Suppose that the corresponding subgroups H and $H'$ of $G_{C^0}$ are equivalent and that the corresponding fields K and $K'$ coincide. Then, ${\text {Jac}}(C)$ and ${\text {Jac}}(C')$ are isogenous.

Proof

Let S be the set of primes of k which are of bad reduction for either ${\text {Jac}}(C)$ or ${\text {Jac}}(C')$ or lie over the fixed prime $\ell$. Note that by [27, Thm. 4.1] the set S contains the primes of k ramified in K or $K'$. By Faltings’ Isogeny Theorem [8, Korollar 2], it suffices to show that for every $\mathfrak {p}\not \in S$, we have

$$\begin{aligned} L_\mathfrak {p}({\text {Jac}}(C),T)=L_\mathfrak {p}({\text {Jac}}(C'),T). \end{aligned}$$

(3.20)

If ${\text {Frob}}_\mathfrak {p}\not \in G_{kM}$, by the proof of Corollary 2.4, both polynomials of (3.20) have the same expression, which depends only on the order of (the projection of) ${\text {Frob}}_\mathfrak {p}$ in $\mathrm {Gal}(K/kM)$. To obtain (3.20) for those $\mathfrak {p}$ such that ${\text {Frob}}_\mathfrak {p}\in G_{kM}$, we will show that $V_\ell ({\text {Jac}}(C)_{kM})$ and $V_\ell ({\text {Jac}}(C')_{kM})$ are isomorphic as $\mathbb Q_\ell [G_{kM}]$-modules. Indeed, the fact that H and $H'$ are equivalent pairs implies that the restrictions from ${\text {Aut}}(C^0_M)$ to $H_0$ and $H_0'$ of the representations $\theta _{E^0,C^0}$ attached to C and $C'$ are equivalent. Together with (3.5), this shows that $\theta _{M,\sigma }(E^0,{\text {Jac}}(C))$ and $\theta _{M,\sigma }(E^0,{\text {Jac}}(C'))$ are equivalent representations. The desired $\mathbb Q_{\ell }[G_{kM}]$-module isomorphism follows now from (2.2).$\square$

Remark 3.31

Let H and $H'$ be any two equivalent pairs attached to twists C and $C'$ of the same curve $C^0$. As one can read from Tables 4 and 5 (and as we will see in the next section), one can choose C and $C'$ so that K and $K'$ coincide. It follows from Proposition 3.30 that on Table 4 (resp. Table 5) two curves C and $C'$ satisfy $\mathrm {ST}(C)=\mathrm {ST}(C')$ if and only if ${\text {Jac}}(C)\sim {\text {Jac}}(C')$.

We conclude this section with an observation that is not directly relevant to our results but illustrates a curious phenomenon arising among the twists of the Fermat quartic in Table 4. Let

$$\begin{aligned} C_5:9x^4+9y^4-4z^4=0 \qquad \text {and}\qquad C_8 :9x^4-4 y^4+z^4=0 \end{aligned}$$

be the curves listed in rows #5 and #8 of Table 4. As can be seen in Table 4, the groups $\mathrm {ST}(C_5)$ and $\mathrm {ST}(C_8)$ coincide, as do the respective fields K. Proposition 3.30 thus implies that the Jacobians of $C_5$ and $C_8$ are isogenous, but in fact more is true.

Proposition 3.32

The curves $C_5$ and $C_8$ are not isomorphic (over $\mathbb Q$), but their reductions $\tilde{C}_5$ and $\tilde{C}_8$ modulo p are isomorphic (over $\mathbb F_p$) for every prime $p>3$.

Proof

The twists $C_5$ are $C_8$ of $C_1^0$ are not isomorphic because they arise from non-conjugate subgroups H of $G_{C_1^0}$. For the reductions $\tilde{C}_5$ and $\tilde{C}_8$, we first consider the case $p\equiv 1 \pmod 4$. We claim that $-4$ is a fourth power modulo p; this follows from the factorization

$$\begin{aligned} x^4+4=(x^2-2x+2)(x^2+2x+2) \qquad \text {in }\mathbb Q[x] \end{aligned}$$

together with the fact that $x^2-2x+2$ and $x^2+2x+2$ have discriminant $-4$. It follows that $\tilde{C}_5$ and $\tilde{C}_8$ are both isomorphic to $9x^4+9y^4+z^4=0$ (over $\mathbb F_p$).

Suppose now that $p\equiv -1 \pmod 4$. Then, 9 is a fourth power modulo p since

$$\begin{aligned} x^4-9=(x^2-3)(x^2+3) \qquad \text {and} \qquad \left( {\begin{array}{c}-3\\ p\end{array}}\right) =-\left( {\begin{array}{c}3\\ p\end{array}}\right) . \end{aligned}$$

It follows that $\tilde{C}_5$ and $\tilde{C}_8$ are both isomorphic to $x^4+y^4-4z^4=0$ (over $\mathbb F_p$).$\square$

3.4 Curve equations

In this section, we construct explicit twists of the Fermat and the Klein quartics realizing each of the subgroups $H\subseteq G_{C^0}$ described in Remark 3.10. Recall that each H has an associated subgroup $H_0:=H\cap G_0$ of index at most 2 (see Definition 3.9), and there exists a twist corresponding to H with $k=kM$ if and only if $H=H_0$, where, as always, M denotes the CM field of $E^0$ (the elliptic curve for which ${\text {Jac}}(C^0)\sim (E^0)^3$).

Equations for these twists are listed in Tables 4 and 5 in Sect. 4. As explained in Remark 3.10, in the Fermat case every subgroup $H\subseteq G_{C^0_1}$ with $[H:H_0]=1$ (case (c$_1$) of Definition 3.9) arises as $H_0'$ for some subgroup $H'\subseteq G_{C^0_1}$ for which $[H':H_0']=2$ (case (c$_2$) of Definition 3.9), and a twist corresponding to H can thus be obtained as the base change to kM of a twist corresponding to $H'$. We thus only list twists for the 59 subgroups H in case (c$_2$), since base changes of these twists to kM then address the 24 subgroups H in case (c$_1$). In the Klein case, we list twists for the 11 subgroups H in case (c$_2$) and also the 3 exceptional subgroups H in case (c$_1$) that cannot be obtained as base changes of twists corresponding to subgroups in case (c$_2$); see Remark 3.10.

Our twists are all defined over base fields k of minimal possible degree, never exceeding 2. For the 3 exceptional subgroups H in the Klein case noted above, we must have $k=kM$, and we use $k=M=\mathbb Q(\sqrt{-7})$. In all but 5 of the remaining cases with $[H:H_0]=2$, we use $k=\mathbb Q$. These 5 exceptions are all explained by Lemma 3.33 below (the second of the 4 pairs listed in Lemma 3.33 arises in both the Fermat and Klein cases, leading to 5 exceptions in total). In each of these 5 exceptions with $[H:H_0]=2$, the subgroup $H_0$ also arises as $H_0'$ for some subgroup $H'\subseteq G_{C_1^0}$ with $[H':H'_0]=2$ that is realized by a twist with $k=\mathbb Q$, allowing $H_0$ to be realized over a quadratic field as the base change to M of a twist defined over $\mathbb Q$.

Lemma 3.33

Twists of the Fermat or Klein quartics corresponding to pairs $(H,H_0)$ with the following pairs of $\mathrm {GAP}$ identifiers cannot be defined over a totally real field:

$$\begin{aligned} (\langle 4,1\rangle ,\langle 2,1\rangle ),\quad (\langle 8,1\rangle ,\langle 4,1\rangle ),\quad (\langle 8,4\rangle ,\langle 4,1\rangle ), \quad (\langle 16,6\rangle ,\langle (8,2\rangle ). \end{aligned}$$

Proof

If k is totally real, then complex conjugation acts trivially on k but not on kM, giving an involution in $H=\mathrm {Gal}(K/k)$ with non-trivial image in $H/H_0=\mathrm {Gal}(K/k)/\mathrm {Gal}(K/kM)$. For the four pairs $(H,H_0)$ listed in the lemma, no such involution exists.$\square$

In addition to listing equations and a field of definition k for a twist C associated with each subgroup H, in Tables 4 and 5 we also list the minimal field K over which all the endomorphisms of ${\text {Jac}}(C)$ are defined, and we identify the conjugacy class of $\mathrm {ST}(C)$ and $\mathrm {ST}(C_{kM})$, which depends only on H, not the particular choice of C. As noted in Remark 3.31, we have chosen twists C so that twists with the same Sato–Tate group have the same fields K and thus have isogenous Jacobians, by Proposition 3.30 (thereby demonstrating that the hypotheses of the proposition can always be satisfied).

3.4.1 Constructing the Fermat twists

The twists of the Fermat curve over any number field are parametrized in [23], and we specialize the parameters in Theorems 4.1, 4.2, 4.5 of [23] to obtain the desired examples. In every case, we are able to obtain equations with coefficients in $\mathbb {Q}$, but as explained above, we cannot always take $k=\mathbb Q$; the exceptions can be found in rows #4, #13, #27, #33 of Table 4. The parameterizations in [23] also allow us to determine the field L over which all the isomorphisms to $(C_7^0)_{\overline{\mathbb Q}}$ are defined, which by Lemma 3.3 and Proposition 3.7, this is the same as the field K over which all the endomorphisms of ${\text {Jac}}(C_7^0)_{\overline{\mathbb Q}}$ are defined.

Specializing the parameters for each of the 59 cases with $k\not = kM$ involves a lot of easy but tedious computations. The resulting equations are typically not particularly pleasing to the eye or easy to format in a table; in order to make them more presentable, we used the algorithm in [30] to simplify the equations. To give just one example, for the unique subgroup H with ID$(H) = \langle 24,13\rangle$, the equation we obtain from specializing the parameterizations in [23] is

$$\begin{aligned} 14x^4&- 84x^3y + 392x^3z + 588x^2y^2 - 2940x^2yz + 4998x^2z^2 - 980xy^3 + 9996xy^2z\\ {}&- 28812xyz^2 + 30184xz^3 + 833y^4 - 9604y^3z + 45276y^2z^2 \\ {}&- 90552yz^3 + 69629z^4 = 0, \end{aligned}$$

but the equation listed for this curve in row #48 of Table 4 is

$$\begin{aligned} 3x^4 + 4x^3y + 4x^3z + 6x^2y^2 + 6x^2z^2 + 8xy^3 + 12xyz^2 + 5y^4 + 4y^3z + 12y^2z^2 + z^4 = 0. \end{aligned}$$

We used of the number field functionality in [6] and [34] to minimize the presentation of the fields K listed in the tables (in particular, the function polredabs in PARI/GP).

3.4.2 Constructing the Klein twists

Twists of the Klein curve over arbitrary number fields are parametrized in Theorems 6.1 and 6.8 of [23], following the method described in [22], which is based on the resolution of certain Galois embedding problems. However, in the most difficult case, in which $H=G_{C_7^0}$ has order 336, this Galois embedding problem is computationally difficult to resolve explicitly. This led us to pursue an alternative approach that exploits the moduli interpretation of twists of the Klein curve as twists of the modular curve X(7). As described in [14, §3] and [25, §4], associated with each elliptic curve $E/\mathbb Q$ is a twist $X_E(7)$ of the Klein quartic defined over $\mathbb Q$ that parameterizes isomorphism classes of 7-torsion Galois modules isomorphic to E[7], as we recall below. With this approach, we can easily treat the case $H=G_{C_7^0}$, and we often obtain twists with nicer equations. In one case, we also obtain a better field of definition k, allowing us to achieve the minimal possible degree $[k:\mathbb Q]$ in every case.

However, as noted in [25, §4.5], not every twist of the Klein curve can be written as $X_E(7)$ for some elliptic curve $E/\mathbb Q$, and there are several subgroups $H\subseteq G_{C_7^0}$ for which the parameterizations in [23] yield a twist of the Klein quartic defined over $\mathbb Q$, but no twists of the form $X_E(7)$ corresponding to H exist. We are thus forced to use a combination of the two approaches. For twists of the form $X_E(7)$, we need to determine the minimal field over which the endomorphisms of ${\text {Jac}}(X_E(7))$ are defined; this is addressed by Propositions 3.34 and 3.35.

Let $E/\mathbb Q$ be an elliptic curve and let E[7] denote the $\mathbb F_7[G_\mathbb Q]$-module of ${\overline{\mathbb Q}}$-valued points of the kernel of the multiplication-by-7 map $[7]:E\rightarrow E$. The Weil pairing gives a $G_\mathbb Q$-equivariant isomorphism $\bigwedge ^2 E[7]\simeq \mu _7$, where $\mu _7$ denotes the $\mathbb F_7[G_\mathbb Q]$-module of 7th roots of unity. Let $Y_E(7)$ be the curve defined over $\mathbb Q$ described in [14, §3] and [25, §4]. For any field extension $L/\mathbb Q$, the L-valued points of $Y_E(7)$ parametrize isomorphism classes of pairs $(E',\phi )$, where $E'/L$ is an elliptic curve and $\phi :E[7]\rightarrow E'[7]$ is a symplectic isomorphism. By a symplectic isomorphism, we mean a $G_L$-equivariant isomorphism $\phi :E[7]\rightarrow E'[7]$ such that the diagram

(3.21)

commutes, where the horizontal arrows are Weil pairings. Two pairs $(E',\phi )$ and $(\tilde{E}', \tilde{\phi })$ are isomorphic whenever there exists an isomorphism $\varepsilon :E'\rightarrow \tilde{E}'$ such that $\tilde{\phi }=\varepsilon \circ \phi$.

In [14] it is shown that $X_E(7)$, the compactification of $Y_E(7)$, is a twist of $C^0_7$, and an explicit model for $X_E(7)$ is given by [14, Thm. 2.1], which states that if E has the Weierstrass model $y^2=x^3+ax+b$ with $a,b\in \mathbb Q$, then

$$\begin{aligned} ax^{4}+7bx^{3}z+3x^{2}y^{2}-3a^{2}x^{2}z^{2}-6bxyz^{2}-5abxz^{3}+2y^{3}z+3ay^{2}z^{2}+2a^{2}yz^{3}-4b^{2}z^{4}=0\, \end{aligned}$$

(3.22)

is a model for $X_E(7)$ defined over $\mathbb Q$.

We will use the moduli interpretation of $X_E(7)$ to determine the minimal field over which all of its automorphisms are defined. Recall that the action of $G_\mathbb Q$ on E[7] gives rise to a Galois representation

$$\begin{aligned} \varrho _{E,7}:G_\mathbb Q\rightarrow {\text {Aut}}(E[7])\simeq \mathrm {GL}_2(\mathbb F_7). \end{aligned}$$

Let $\overline{\varrho }_{E,7}$ denote the composition $\pi \circ \varrho _{E,7}$, where $\pi :\mathrm {GL}_2(\mathbb F_7)\rightarrow \mathrm {PGL}_2(\mathbb F_7)$ is the natural projection.

Proposition 3.34

The following field extensions of $\mathbb Q$ coincide:

• (i) The minimal extension over which all endomorphisms of ${\text {Jac}}(X_E(7))$ are defined;

• (ii) The minimal extension over which all automorphisms of $X_E(7)$ are defined;

• (iii) The field $\overline{\mathbb Q}^{\ker \overline{\varrho }_{E,7}}$;

• (iv) The minimal extension over which all 7-isogenies of E are defined.

In particular, if K is the field determined by these equivalent conditions, then

$$\begin{aligned} \mathrm {Gal}(K/\mathbb Q)\simeq \mathrm {Im}(\overline{\varrho }_{E,7}) \simeq \mathrm {Im}(\varrho _{E,7}) / (\mathrm {Im}\varrho _{E,7} \cap \mathbb F_7^\times ). \end{aligned}$$

Proof

The equivalence of (i) and (ii) follows from 3.3, since $X_E(7)$ is a twist of $C^0_7$.

Following [25], let ${\text {Aut}}_{\wedge }(E[7])$ denote the group of symplectic automorphisms of E[7]. Given a field extension $F/\mathbb Q$, let us write $E[7]_F$ for the $\mathbb F_7[G_F]$-module obtained from E[7] by restriction from $G_\mathbb Q$ to $G_F$. Note that $E[7]_{\overline{\mathbb Q}}\simeq (\mathbb Z/7\mathbb Z)^2$. Under this isomorphism, for any $g\in {\text {Aut}}_{\wedge }(E[7]_{\overline{\mathbb Q}})$, diagram (3.21) becomes

from which we deduce

$$\begin{aligned} {\text {Aut}}_{\wedge }(E[7]_{\overline{\mathbb Q}})\simeq \mathrm {SL}_2(\mathbb F_7). \end{aligned}$$

(3.23)

Each $g\in {\text {Aut}}_{\wedge }(E[7]_{\overline{\mathbb Q}})$ acts on $Y_E(7)_{\overline{\mathbb Q}}$ via $(E',\phi )\mapsto (E',\phi \circ g^{-1})$. This action extends to $X_E(7)$, from which we obtain a homomorphism

$$\begin{aligned} {\text {Aut}}_\wedge (E[7]_{\overline{\mathbb Q}})\rightarrow {\text {Aut}}(X_E(7)_{\overline{\mathbb Q}}). \end{aligned}$$

(3.24)

This homomorphism is non-trivial, since elements of its kernel induce automorphisms of $E_{\overline{\mathbb Q}}$, but ${\text {Aut}}(E_{\overline{\mathbb Q}})$ is abelian and ${\text {Aut}}_\wedge (E[7])_{\overline{\mathbb Q}}\simeq \mathrm {SL}_2(\mathbb F_7)$ is not, and it cannot be injective, since the group on the right has cardinality $168 < \#\mathrm {SL}_2(\mathbb F_7)=336$. The only non-trivial proper normal subgroup of $\mathrm {SL}_2(\mathbb F_7)$ is $\langle \pm 1\rangle$, and thus (3.24) induces a $G_\mathbb Q$-equivariant isomorphism

$$\begin{aligned} {\text {Aut}}_\wedge (E[7])/\langle \pm 1\rangle \rightarrow {\text {Aut}}(X_E(7)_{\overline{\mathbb Q}}). \end{aligned}$$

(3.25)

By transport of structure, we now endow $\mathrm {SL}_2(\mathbb F_7)$ with a $G_\mathbb Q$-module structure that turns (3.23) into a $G_\mathbb Q$-equivariant isomorphism $\varphi :{\text {Aut}}_\wedge (E[7]_{\overline{\mathbb Q}})\overset{\sim }{\rightarrow }\mathrm {SL}_2(\mathbb F_7)$. Now define $\varrho :G_\mathbb Q\rightarrow {\text {Aut}}(\mathrm {SL}_2(\mathbb F_7))$ to be the representation associated with this $G_\mathbb Q$-module structure. Since the action of $\sigma \in G_\mathbb Q$ on each $g \in {\text {Aut}}_{\wedge }(E[7]_{\overline{\mathbb Q}})$ is defined by

$$\begin{aligned} ({}^\sigma g)(P)={}^\sigma (g({}^{\sigma ^{-1}}P)), \end{aligned}$$

for $P\in E[7]$, we have $\varrho (\sigma ) (\varphi (g))= \varrho _{E,7}(\sigma )\cdot \varphi (g)\cdot \varrho _{E,7}(\sigma )^{-1}$. The $\mathrm {G}_\mathbb Q$-action is trivial on $\langle \pm 1\rangle$ and thus descends to $\mathrm {PSL}_2(\mathbb F_7)$. Let us write $\mathrm {PSL}_2(\mathbb F_7)^{\varrho }$ for $\mathrm {PSL}_2(\mathbb F_7)$ endowed with the $G_\mathbb Q$-action given by conjugation by $\varrho _{E,7}$. Then, (3.23) with (3.25) yield a $G_\mathbb Q$-equivariant isomorphism

$$\begin{aligned} \mathrm {PSL}_2(\mathbb F_7)^{\varrho }\simeq {\text {Aut}}(X_E(7)_{\overline{\mathbb Q}}) . \end{aligned}$$

This implies that the field described in (ii) coincides with ${\overline{\mathbb Q}}^{{\text {Ker}}(\varrho )}$, and we now note that

$$\begin{aligned} \ker (\varrho )&=\{\sigma \in G_\mathbb Q\,|\,\varrho _{E,7}(\sigma )\cdot \alpha \cdot \varrho _{E,7}(\sigma )^{-1}=\alpha ,\,\text {for all }\alpha \in \mathrm {PSL}_2(\mathbb F_7)\}\\&=\{\sigma \in G_\mathbb Q\,|\,\varrho _{E,7}(\sigma )\in \mathbb F_7^\times \}\\&=\ker (\overline{\varrho }_{E,7}), \end{aligned}$$

thus ${\overline{\mathbb Q}}^{\ker (\varrho )}={\overline{\mathbb Q}}^{\ker (\varrho _{E,7})}$ is the field described in (iii).

Now let $\mathbb P(E[7])$ denote the projective space over E[7], consisting of its 8 linear $\mathbb F_7$-subspaces, equivalently, its 8 cyclic subgroups of order 7. The $G_\mathbb Q$-action on $\mathbb P(E[7])$ gives rise to the projective Galois representation

$$\begin{aligned} \overline{\varrho }_{E,7}:G_\mathbb Q\rightarrow {\text {Aut}}(\mathbb P(E[7]))\simeq \mathrm {PGL}_2(\mathbb F_7). \end{aligned}$$

The minimal field extension K over which the $G_K$-action on $\mathbb P(E[7])$ becomes trivial is precisely the minimal field over which the cyclic subgroups of E[7] of order 7 all become Galois stable, equivalently, the minimal field over which all the 7-isogenies of E are defined. It follows that the fixed field of $\ker \overline{\varrho }_{E,7}$ identified in (iii) is also the field described in (iv).$\square$

To explicitly determine the field over which all the 7-isogenies of E are defined, we rely on Proposition 3.35 below, in which $\Phi _7(X,Y)\in \mathbb Z[X,Y]$ denotes the classical modular polynomial; the equation for $\Phi _7(X,Y)$ is too large to print here, but it is available in [6] and can be found in the tables of modular polynomials listed in [33] that were computed via [5]; it is a symmetric in X and Y, and has degree 8 in both variables.

The equation $\Phi _7(X,Y)=0$ is a canonical (singular) model for the modular curve $Y_0(7)$ that parameterizes 7-isogenies. If $E_1$ and $E_2$ are elliptic curves related by a 7-isogeny then $\Phi _7(j(E_1),j(E_2))=0$, and if $j_1,j_2\in F$ satisfy $\Phi _7(j_1,j_2)=0$, then there exist elliptic curves $E_1$ and $E_2$ with $j(E_1)=j_1$ and $j(E_2)=j_2$ that are related by a 7-isogeny. However, this 7-isogeny need not be defined over F! The following proposition characterizes the relationship between F and the minimal field K over which all the 7-isogenies of E are defined.

Proposition 3.35

Let E be an elliptic curve over a number field k with $j(E)\ne 0,1728$. Let F be the splitting field of $\Phi _7(j(E),Y)\in k[X]$, and let K be the minimal field over which all the 7-isogenies of E are defined. The fields K and F coincide.

Proof

Let S be the multiset of roots of $\Phi _7(j(E),Y)$ in ${\overline{\mathbb Q}}$, viewed as a $G_k$-set in which the action of $\sigma \in G_k$ preserves multiplicities: we have $m(\sigma (r))=m(r)$ for all $\sigma \in G_k$, where m(r) denotes the multiplicity of r in S. Let $\mathbb {P}(E[7])$ be the $G_k$-set of cyclic subgroups $\langle P\rangle$ of E[7] of order 7. In characteristic zero every isogeny is separable, hence determined by its kernel up to composition with automorphisms; this yields a surjective morphism of $G_k$-sets $\varphi :\mathbb {P}(E[7])\rightarrow S$ defined by $\langle P\rangle \mapsto j(E/\langle P\rangle )$ with $m(r)=\#\varphi ^{-1}(r)$ for all $r\in S$ (note $\#\mathbb {P}(E[7])=8=\sum _{r\in S}m(r)$). The $G_k$-action on S factors through the $G_k$-action on $\mathbb {P}(E[7])$, and we thus have group homomorphisms

$$\begin{aligned} G_k\overset{\bar{\varrho }_{E,7}}{\longrightarrow } {\text {Aut}}(\mathbb {P}(E[7])\overset{\phi }{\longrightarrow } {\text {Aut}}(S), \end{aligned}$$

where $\phi :\bar{\varrho }_{E,7}(G_k)\rightarrow {\text {Aut}}(S)$ is defined by $\phi (\sigma )(\varphi (\langle P\rangle ):=\varphi (\sigma (\langle P\rangle ))$ for each $\sigma \in \bar{\varrho }_{E,7}(G_k)$. We then have $K={\overline{\mathbb Q}}^{\ker \bar{\varrho }_{E,7}}$ and $F={\overline{\mathbb Q}}^{\ker (\phi \circ \bar{\varrho }_{E,7})}$, so $F\subseteq K$.

If E does not have complex multiplication, then $m(r)=1$ for all $r\in S$, since otherwise over ${\overline{\mathbb Q}}$ we would have two 7-isogenies $\alpha ,\beta :E_{{\overline{\mathbb Q}}}\rightarrow E'$ with distinct kernels, and then $(\hat{\alpha }\circ \beta )\in {\text {End}}(E_{{\overline{\mathbb Q}}})$ is an endomorphism of degree 49 which is not $\pm 7$, contradicting ${\text {End}}(E_{{\overline{\mathbb Q}}})\simeq \mathbb Z$. It follows that $\varphi$ and therefore $\phi$ is injective, so $\ker \bar{\varrho }_{E,7}=\ker (\phi \circ \bar{\varrho }_{E,7})$ and $K=F$.

If E does have complex multiplication, then ${\text {End}}(E_{{\overline{\mathbb Q}}})$ is isomorphic to an order in an imaginary quadratic field M. We now consider the isogeny graph whose vertices are j-invariants of elliptic curves $E'/FM$ with edges $(j_1,j_2)$ present with multiplicity equal to the multiplicity of $j_2$ as a root of $\Phi _7(j_1,Y)$. Since $j(E)\ne 0,1728$, the component of $j(E_{FM})$ in this graph is an isogeny volcano, as defined in [31]. In particular, there are at least 6 distinct edges $(j(E_{FM}),j_2)$ (edges with multiplicity greater than 1 can occur only at the surface of an isogeny volcano and the subgraph on the surface is regular of degree at most 2). It follows that $m(r)>1$ for at most one $r\in S$.

The image of $\bar{\varrho }_{E,7}$ is isomorphic to a subgroup of $\mathrm {PGL}_2(\mathbb F_7)$, and this implies that if $\bar{\varrho }_{E,7}(\sigma )$ fixes more than 2 elements of $\mathbb {P}(E[7])$ then $\sigma \in \ker \bar{\varrho }_{E,7}$. This necessarily applies whenever $\bar{\varrho }_{E,7}(\sigma )$ lies in $\ker \phi$, since it must fix 6 elements, thus $\ker \bar{\varrho }_{E,7}=\ker (\phi \circ \bar{\varrho }_{E,7})$ and $K=F$.$\square$

Corollary 3.36

Let E be an elliptic curve over a number field k with $j(E)\ne 0,1728$. The minimal field K over which all the 7-isogenies of E are defined depends only on j(E).

Remark 3.37

The first part of the proof of Proposition 3.35 also applies when j(E) is 0 or 1728, thus we always have $F\subseteq K$. Equality does not hold in general, but a direct computation finds that $[K\!:\!F]$ must divide 6 (resp. 2) when $j(E)=0$ (resp. 1728), and this occurs when $k=\mathbb Q$.

We now fix E as the elliptic curve $y^{2}=x^{3}+6x+7$ with Cremona label 144b1. Note that $\varrho _{E,7}$ is surjective; this can be seen in the entry for this curve in the L-functions and Modular Forms Database [35] and was determined by the algorithm in [32]. It follows that $\mathrm {Gal}(\mathbb Q(E[7])/\mathbb Q)\simeq \mathrm {GL}_2(\mathbb F_7)$, and Proposition 3.34 implies that we then have $H:=\mathrm {Gal}(K/\mathbb Q)\simeq \mathrm {PGL}_2(\mathbb F_7)$.

For our chosen curve E, we have $a=6$ and $b=7$. Plugging these values into equation (3.22) and applying the algorithm of [30] to simplify the result yields the curve listed in entry #14 of Table 5 for $H=G_{C_7^0}$. To determine the field K, we apply Proposition 3.35. Plugging $j(E)=48384$ into $\Phi _7(x,j(E))$ and using PARI/GP to simplify the resulting polynomial, we find that K is the splitting field of the polynomial ${x^8 + 4x^7 + 21x^4 + 18x + 9}$.

We applied the same procedure to obtain the equations for C and the polynomials defining K that are listed in rows #4, #6, #9, #10 of Table 5 using the elliptic curves E with Cremona labels 2450ba1, 64a4, 784h1, 36a1, respectively, with appropriate adjustments for the cases with $j(E)=0,1728$ as indicated in Proposition 3.35. The curve in row #11 is a base change of the curve in row #6, and for the remaining 7 curves we used the parameterizations in [23].

3.5 Numerical computations

In the previous sections, we have described the explicit computation of several quantities related to twists C of $C^0=C^0_d$, where $C^0_d$ is our fixed model over $\mathbb Q$ for the Fermat quartic ($d=1$) or the Klein quartic ($d=7$), with ${\text {Jac}}(C^0)\sim (E^0)^3$, where $E^0=E^0_d$ is an elliptic curve over $\mathbb Q$ with CM by $M=\mathbb Q(\sqrt{-d})$ defined in (3.1). These include:

• Explicit equations for twists C of $C^0$ corresponding to subgroups H of $G_{C^0}$;

• Defining polynomials for the minimal field K for which ${\text {End}}({\text {Jac}}(C)_K)={\text {End}}({\text {Jac}}(C)_{\overline{\mathbb Q}})$;

• Independent and joint coefficient moments of the Sato–Tate groups $\mathrm {ST}({\text {Jac}}(C))$.

These computations are numerous and lengthy, leaving many opportunities for errors, both by human and by machine. We performed several numerical tests to verify our computations.

3.5.1 Naïve point-counting

A simple but effective way to test the compatibility of a twist C / k and endomorphism field K is to verify that for the first several degree one primes $\mathfrak {p}$ of k of good reduction for C that split completely in K, the reduction of ${\text {Jac}}(C)$ modulo $\mathfrak {p}$ is isogenous to the cube of the reduction of $E^0$ modulo the prime $p:=N(\mathfrak {p})$. By a theorem of Tate, it suffices to check that $L_\mathfrak {p}({\text {Jac}}(C),T)=L_p(E^0,T)^3$. For this task, we used optimized brute force point-counting methods adapted from [20, §3]. The L-polynomial $L_\mathfrak {p}({\text {Jac}}(C),T)$ is the numerator of the zeta function of C, a genus 3 curve, so it suffices to compute $\#C(\mathbb F_p)$, $\#C(\mathbb F_{p^2})$, $\#C(\mathbb F_{p^3})$, reducing the problem to counting points on smooth plane quartics and elliptic curves over finite fields.

To count projective points (x : y : z) on a smooth plane quartic $f(x,y,z)=0$ over a finite field $\mathbb F_q$, one first counts affine points (x : y : 1) by iterating over $a\in \mathbb F_q$, computing the number r of distinct $\mathbb F_q$-rational roots of $g_a(x):=f(x,a,1)$ via $r=\deg (\gcd (x^q-x,g_a(x)))$, and then determining the multiplicity of each rational root by determining the least $n\ge 1$ for which $\gcd (g_a(x),g^{(n)}_a(x))=1$, where $g^{(n)}_a$ denotes the nth derivative of $g_a\in \mathbb F_q[x]$; note that to compute $\gcd (x^q-x,g_a(x))$ one first computes $x^q\bmod g_a(x)$ using a square-and-multiply algorithm. Having counted affine points (x : y : 1), one then counts the $\mathbb F_q$-rational roots of f(x, 1, 0) and finally checks whether (1 : 0 : 0) is a point on the curve.

To optimize this procedure, one first seeks a linear transformation of f(x, y, z) that ensures $g_a(x)=f(x,a,1)$ has degree at most 3 for all $a\in \mathbb F_q$; for this, it suffices to translate a rational point to (1 : 0 : 0), which is always possible for $q\ge 37$ (by the Weil bounds). This yields an $O(p^3(\log p)^{2+o(1)})$-time algorithm to compute $L_\mathfrak {p}({\text {Jac}}(C),T)$ that is quite practical for p up to $2^{12}$, enough to find several (possibly hundreds) of degree one primes $\mathfrak {p}$ of k that split completely in K.

Having computed $L_\mathfrak {p}({\text {Jac}}(C),T)$, one compares this to $L_p(E^0,T)^3$; note that the polynomial $L_p(E^0,T)=pT^2-a_pT+1$ is easily computed via $a_p=p+1-\#E^0(\mathbb F_p)$. If this comparison fails, then either C is not a twist of $C^0$, or not all of the endomorphisms of ${\text {Jac}}(C)_{\overline{\mathbb Q}}$ are defined over K. The converse is of course false, but if this comparison succeeds for many degree-1 primes $\mathfrak {p}$ it gives one a high degree of confidence in the computations of C and K.⁴ Note that this test will succeed even when K is not minimal, but we also check that $H\simeq \mathrm {Gal}(K/k)$, which means that so long as C is a twist of $C^0$ corresponding to the subgroup $H\subseteq G_{C_0}$, the field K must be minimal.

3.5.2 An average polynomial-time algorithm

In order to numerically test our computations of the Sato–Tate groups $\mathrm {ST}(C)$, and to verify our computation of the coefficient moments, we also computed Sato–Tate statistics for all of our twists C / k of the Fermat and Klein quartics. This requires computing the L-polynomials $L_\mathfrak {p}({\text {Jac}}(C),T)$ at primes $\mathfrak {p}$ of good reduction for C up to some bound N, and it suffices to consider only primes $\mathfrak {p}$ of prime norm $p=N(\mathfrak {p})$, since nearly all the primes of norm less than N are degree-1 primes. In order to get statistics that are close to the values predicted by the Sato–Tate group one needs N to be fairly large. We used $N=2^{26}$, which is far too large for the naive $O(p^3(\log p)^{2+o(1)})$-time algorithm described above to be practical, even for a single prime $p\approx N$, let alone all good $p\le N$.

In [18], Harvey and Sutherland give an average polynomial-time algorithm to count points on smooth plane quartics over $\mathbb Q$ that allows one to compute $L_p({\text {Jac}}(C),T)\bmod p$ for all good primes $p\le N$ in time $O(N(\log N)^{3+o(1)})$, which represents an average cost of $O((\log p)^{4+o(1)})$ per prime $p\le N$. This is achieved by computing the Hasse–Witt matrices of the reductions of C modulo p using a generalization of the approach given in [16, 17] for hyperelliptic curves. In [18], they also give an $O(\sqrt{p}(\log p)^{1+o(1)})$-time algorithm to compute $L_p({\text {Jac}}(C),T)\bmod p$ for a single good prime p, which allows one to handle reductions of smooth plane quartics C defined over number fields at degree one primes; this increases the total running time for $p\le N$ to $O(N^{3/2+o(1)})$, which is still feasible with $N=2^{26}$.

Having computed $L_p({\text {Jac}}(C),T)\bmod p$, we need to lift this polynomial for $(\mathbb Z/p\mathbb Z)[T]$ to $\mathbb Z[T]$, which is facilitated by Proposition 3.38 below. It follows from the Weil bounds that the linear coefficient of $L_p({\text {Jac}}(C),T)$ is an integer of absolute value at most $6\sqrt{p}$. For $p>144$, the value of this integer is uniquely determined by its value modulo p, and for $p<144$ we can apply the naive approach described above. This uniquely determines the value in the column labeled $F_1(x)$ in Tables 1 and 2 of Proposition 3.38, which then determines the values in columns $F_2(x)$ and $F_3(s)$, allowing the integer polynomial $L_p({\text {Jac}}(C),T)\in \mathbb Z[T]$ to be completely determined.

Proposition 3.38

For $\tau$ in $\mathrm {Gal}(L/k)$, let $s=s(\tau )$ and $t=t(\tau )$ denote the orders of $\tau$ and the projection of $\tau$ on $\mathrm {Gal}(kM/k)$, respectively. For C a twist of $C^0$, the following hold:

• (i) The pair (s, t) is one of the 9 pairs listed on Table 1 if $C^0=C^0_1$, and one of the 9 pairs listed on Table 2 if $C^0=C^0_7$.

• (ii) For each pair (s, t), let

  $$\begin{aligned} F_{(s,t)}:=F_{1}\times F_{2}\times F_{3}:[-2,2]\rightarrow [-6,6]\times [-1,15]\times [-20,20]\subseteq \mathbb R^3 \end{aligned}$$

  be the map defined in Table 1 if $C_0=C_0^1$ or Table 2 if $C_0=C_0^7$. For every prime $\mathfrak {p}$ unramified in K of good reduction for both ${\text {Jac}}(C)$ and $E^0$, we have

  $$\begin{aligned} F_{(f_L(\mathfrak {p}),f_{kM}(\mathfrak {p}))}(a_1(E^0)(\mathfrak {p}))=\bigl ( a_1({\text {Jac}}(C))( \mathfrak {p}), a_2({\text {Jac}}(C))(\mathfrak {p}), a_3({\text {Jac}}(C))(\mathfrak {p}) \bigr ), \end{aligned}$$

  (3.26)

  where $f_L(\mathfrak {p})$ (resp. $f_{kM}(\mathfrak {p})$) is the residue degree of $\mathfrak {p}$ in L (resp. kM).

Table 1 For each possible pair (s, t), the corresponding values of $F_{(s,t)}(x)$ if $C^0=C^0_1$. In the table below, y denotes $\pm \sqrt{4-x^2}$

Table 2 For each possible pair (s, t), the corresponding values of $F_{(s,t)}(x)$ if $C^0=C^0_7$. In the table below, y denotes $\pm \sqrt{(4-x^2)/7}$

Table 3 Character tables of ${\text {Aut}}(C^0_M)$. See (3.2) and (3.3) for the generators s, t, u

Table 4 Twists of the Fermat quartic corresponding to subgroups $H \subseteq G_{C^0_1}$. See (3.2) for the definitions of s, t, u and (3.6) for the definition of h. We identify $\mathrm {ST}_k=\mathrm {ST}(C)$ and $\mathrm {ST}_{kM}=\mathrm {ST}(C_{kM})$ by row numbers in Table 6; here $M=\mathbb Q(i)$

Table 5 Twists of the Klein quartic corresponding to subgroups $H\subseteq G_{C^0_7}$. See (3.3) for the definitions of s, t, u and see (3.6) for the definition of h. We identify $\mathrm {ST}_k=\mathrm {ST}(C)$ and $\mathrm {ST}_{kM}=\mathrm {ST}(C_{kM})$ by row numbers in Table 6; here $M=\mathbb Q(\sqrt{-7})$ and $a:=(-1+\sqrt{-7})/2$

Table 6 The 60 Sato–Tate distributions arising for Fermat and Klein twists

Table 7 Sato–Tate statistics for Fermat twists over degree one primes $p\le 2^{26}$

Table 8 Sato–Tate statistics for Klein twists over degree one primes $p\le 2^{26}$

Proof

For every prime $\mathfrak {p}$ unramified in K of good reduction for both ${\text {Jac}}(C)$ and $E^0$, write $x_\mathfrak {p}:=a_1(E^0)(\mathfrak {p})$ and $y_\mathfrak {p}:=\pm \sqrt{4-x_\mathfrak {p}^2}$. It follows from the proof of Proposition 2.2 that

$$\begin{aligned} a_1({\text {Jac}}(C))(\mathfrak {p})&= -{\text {Re}}(a_1(\mathfrak {p}))x_\mathfrak {p}+{\text {Im}}( a_1(\mathfrak {p}))y_\mathfrak {p},\\ a_2({\text {Jac}}(C)(\mathfrak {p}))&={\text {Re}}(a_2(\mathfrak {p}))(x_\mathfrak {p}^2-2)- {\text {Im}}(a_2(\mathfrak {p}))x_\mathfrak {p}y_\mathfrak {p}+|a_1(\mathfrak {p})|^2,\\ a_3({\text {Jac}}(C)(\mathfrak {p}))&= -a_3(\mathfrak {p})(x_\mathfrak {p}^3-3x_\mathfrak {p})-{\text {Re}}(\overline{a}_1(\mathfrak {p})a_2(\mathfrak {p}))x_\mathfrak {p}+ {\text {Im}}(\overline{a}_1(\mathfrak {p})a_2(\mathfrak {p}))y_\mathfrak {p}, \end{aligned}$$

from which one can easily derive the assertion of the proposition.$\square$

Tables 7 and 8 show Sato–Tate statistics for the Fermat and Klein twists C / k and their base changes $C_{kM}$. In each row, we list moment statistics $\overline{\mathrm {M }}_{101}, \overline{\mathrm {M }}_{030}, \overline{\mathrm {M }}_{202}$ for the three moments $\mathrm {M }_{101}, \mathrm {M }_{030}, \mathrm {M }_{202}$ that uniquely determine the Sato–Tate group $\mathrm {ST}(C)$, by Proposition 3.13. These were computed by averaging over all good primes of degree one and norm $p\le 2^{26}$.

For comparison, we also list the actual value of each moment, computed using the method described in Sect. 3.2.2. In every case, the moment statistics agree with the corresponding moments of the Sato–Tate groups to within 1.5 percent, and in almost all cases, to within 0.5 percent.

4 Tables

In this final section, we present tables of characters, curves, Sato–Tate distributions, and moment statistics referred to elsewhere in this article. Let us briefly describe their contents.

Table 3 lists characters of the automorphism groups of the Fermat and Klein quartics specified via conjugacy class representatives expressed using the generators s, t, u defined in (3.2) and (3.3).

Tables 4 and 5 list explicit curve equations for twists C of the Fermat and Klein quartics corresponding to subgroups H of $G_{C^0}:={\text {Aut}}(C^0_{M})\rtimes \mathrm {Gal}(M/\mathbb Q)$, as described in Remark 3.10. The group $H_0:=H\cap {\text {Aut}}(C^0_{M})$ is specified in terms of the generators s, t, u listed in (3.2) and (3.3). When $kM=k$ we have $H=H_0$, and otherwise H is specified by listing an element $h\in {\text {Aut}}(C_M^0)$ for which $H=H_0\cup H_0\cdot (h,\tau )$, where $\mathrm {Gal}(M/\mathbb Q)=\langle \tau \rangle$; see (3.6). The isomorphism classes of H and $H_0$ are specified by GAP identifiers $\mathrm {ID}(H)$ and $\mathrm {ID}(H_0)$. The minimal field K over which all endomorphisms of ${\text {Jac}}(C_{\overline{\mathbb Q}})$ are defined is given as an explicit extension of $\mathbb Q$, or as the splitting field $\mathrm {Gal}(f(x))$ of a monic $f\in \mathbb Z[x]$. In the last 2 columns of Tables 4 and 5 we identify the Sato–Tate distributions of $\mathrm {ST}(C)$ and $\mathrm {ST}(C_{kM})$ by their row numbers in Table 6. Among twists with the same Sato–Tate group $\mathrm {ST}(C)$ (which is uniquely identified by its distribution), we list curves with isogenous Jacobians, per Remark 3.31.

In Table 6, we list the 60 Sato–Tate distributions that arise among twists of the Fermat and Klein quartics. Each component group is identified by its GAP ID, and we list the joint moments $\mathrm {M }_{101}$, $\mathrm {M }_{030}$, $\mathrm {M }_{202}$ sufficient to uniquely determine the Sato–Tate distribution, along with the first two non-trivial independent coefficient moments for $a_1,a_2,a_3$. We also list the proportion $z_{i,j}$ of components on which the coefficient $a_i$ takes the fixed integer value j; for $i=1,3$ we list only $z_1:=z_{1,0}$ and $z_3:=z_{3,0}$, and for $i=2$ we list the vector $z_2:=[z_{2,-1},z_{2,0},z_{2,1},z_{2,2},z_{2,3}]$; see Lemma 3.15 for details. There are 6 pairs of Sato–Tate distributions whose independent coefficient measures coincide; these pairs are identified by roman letters that appear in the last column.

Tables 7 and 8 list moment statistics for twists of the Fermat and Klein quartics computed over good primes $p\le 2^{26}$, along with the corresponding moment values. Twists with isogenous Jacobians necessarily have the same moment statistics, so we list only one twist in each isogeny class.

Acknowledgements

We thank Josep González for his help with Lemma 3.18, and we are grateful to the Banff International Research Station for hosting a May 2017 workshop on Arithmetic Aspects of Explicit Moduli Problems where we worked on this article. Fité is grateful to the University of California at San Diego for hosting his visit in spring 2012, the period in which this project was conceived. Fité received financial support from the German Research Council (CRC 701), the Excellence Program María de Maeztu MDM-2014-0445, and MTM2015-63829-P. Sutherland was supported by NSF Grants DMS-1115455 and DMS-1522526. This project has received funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (Grant Agreement No. 682152), and from the Simons Foundation (Grant #550033).