The block planning approach for continuous time-based dynamic lot sizing and scheduling

Abstract

This paper calls for a change in paradigm in lot sizing and scheduling. Traditionally, a discrete time scale is chosen to model lot sizing and scheduling. As an alternative, the so-called block planning concept is proposed which is based on a continuous representation of time. A mixed-integer linear optimization model is presented that determines the size and the time phasing of the individual production lots in a single-stage production system under the objective of minimizing the makespan. The modelling approach presented here assumes the grouping of product variants into setup families and the production of product variants within a family in a pre-defined sequence. Numerical results demonstrate the practicability of this approach under experimental conditions which reflect typical settings from a leading company in the European beverage industry.

1 Introduction

Dynamic lot sizing and scheduling is a key issue in almost all manufacturing systems, especially, when multiple products with volatile demand are produced on the same production equipment. In his seminal work published in 1913, Harris raised the fundamental question “How many parts to make at once?” and proposed the famous classic lot-sizing model for determining optimal lot sizes under static demand conditions. In the following decades, discrete time-based lot-sizing models were introduced to cope with dynamic demand conditions (Wagner and Whitin 1958). In the sequel, capacitated lot-sizing models were derived from this classic dynamic lot-sizing model (Dixon and Silver 1981; Günther 1987; Ross and Almada-Lobo 2011). Clearly, rapidly changing business conditions impose new challenges on the design and industrial application of lot-sizing models. For instance, the following observations give reasons to reconsider the current principles of lot size modelling and call for a change of paradigm.

First, shorter product lifecycles and mass customization lead to a steadily increasing complexity of production systems. This holds, for instance, for technical and chemical goods which are often adapted to the specific processing conditions of the customers. The trend of increased product variety is even more pronounced in the consumer goods industry due to the diversification of package sizes, the use of customized package prints and labels, and the variation of ingredients and flavours.

Second, customers in many industries are seeking faster replenishment and shortened cycle times to reduce their inventories and their investment in storage facilities. This development comes along with the above-mentioned increased product variety. As a consequence, in order not to build up excessive inventories particularly for product variants with low and infrequent demand, manufacturers are often forced to shift part of their production system from make-to-stock (MTS) to make-to-order (MTO) and to apply a hybrid MTS/MTO strategy (Soman et al. 2007). This makes it necessary to implement more flexible manufacturing and more responsive planning systems and to realize smaller lot sizes with frequent changeovers between product variants. In addition, daily due dates or even time windows comprising only a few hours are often defined for the delivery of goods to customers’ distribution centres (Günther and Seiler 2009).

Third, especially in process-related industries, there is often a natural sequence in which the various products are to be produced to minimize total changeover time and to maintain product quality standards. For example, setups are sequenced from products with high to low purity requirements, from the lower taste of a food product to the stronger, or from the brighter colour of a product to the darker (Lütke Entrup et al. 2005). Hence, families of products can be identified which are produced in a given sequence under the same basic equipment setup. In this case, major setups are incurred for changing over between product families while only minor setups are needed for switching to another product within the same family. Hence, lot-sizing models need to reflect the nature of setup drivers and the corresponding hierarchy of setup operations.

Fourth, since the development of the first dynamic lot-sizing models production speed in almost all industries has considerably increased due to rapidly progressing technical advancements. This in combination with the increased number of product variants makes it necessary to base discrete lot-sizing models on an accordingly shorter period length which in turn causes a significant increase in the number of variables and constraints. At the same time, setup effort is often considerably reduced or even eliminated due to automated manufacturing technologies.

Finally, many companies shifted their production control philosophy from push, e.g. the classic material requirements (MRP) planning, to pull systems (Karrer et al. 2012). Consequently, forecast-driven advanced planning of production runs over multiple weeks or months has been replaced by short-term creation of production schedules which are most often driven by call orders from contract customers.

Since in our view conventional lot sizing and scheduling models do not sufficiently reflect the conditions given in industrial production systems we propose an alternate approach, called block planning, for scheduling production orders on a continuous time scale with demand elements being assigned to distinct delivery dates. Moreover, issues like definition of setup families with consideration of major and minor setup times and multiple non-identical production lines with dedicated product-line assignments can be addressed in a realistic way. In the basic block planning model developed in Günther et al. (2006), only one block per period was assumed. Though blocks were allowed to start prior to the assigned period, the degree of flexibility in the generation of the production schedules was still somewhat limited. This paper generalizes and extends the basic block planning model by redefining the decision variables similar to Denizel and Süral (2006) and thus eliminating inventory variables and balance equations. In addition, a flexible assignment of product families to production runs is introduced considering major setups for product families and minor setups for individual items within a family. Further extensions include the consideration of numerous demand elements with specific delivery dates not being confined to period boundaries, the implicit observation of shelf life through the definition of adequate time windows for the assignment of production runs to demand elements, and the reduction of the number of binary variables through the analysis of run-out times for stock-keeping units.

The remainder of this article is organized as follows. In the next section the basic techniques for lot size modelling are discussed. In Sect. 3, the major characteristics of the block planning concept are explained. In the subsequent Sect. 4, a block planning model based on mixed-integer linear programming is developed. Numerical investigations presented in Sect. 5 show the practical applicability of the proposed block planning approach. Finally, some conclusions are drawn.

2 Lot size modelling: review and discussion

The following short review focuses on basic modelling techniques for dynamic capacitated lot sizing. It is not intended here to give a detailed assessment of the many variants of lot-sizing models and solution methods presented in the academic literature. Recently, several comprehensive reviews have been published which focus on specific aspects of lot sizing and scheduling. For instance, Karimi et al. (2003), Quadt and Kuhn (2008) and Buschkühl et al. (2010) review the literature on capacitated lot-sizing problems. Allahverdi et al. (2008) provide a comprehensive review of scheduling problems with sequence-dependent setup times and costs. The review of Zhu and Wilhelm (2006) specifically addresses models and solution approaches for lot sizing with sequence-dependent setups. Robinson et al. (2009) provide a state-of-the-art review of research on coordinated lot sizing. Another recent paper by Jans and Degraeve (2008) reviews the lot-sizing literature from an industrial application perspective.

In the following, we focus on the development stages of the basic modelling techniques. In this regard, three categories of dynamic capacitated lot-sizing models can be identified: (1) pure discrete time-based models, (2) hybrid, i.e. combined discrete–continuous models, and (3) continuous time-based models.

The first category of lot-sizing models subdivides the entire planning horizon into discrete periods, usually of equal length, and determines setup decisions, lot sizes and inventory levels for each product and period (Suerie 2005). Two variants of this modelling approach exist. Big-bucket models assume a basic period length which is sufficient to schedule several production lots per period. The main difficulty associated with this approach is that the sequencing and timing of the production runs within a period and the possible carryover of the setup state between periods is not explicitly modelled. In contrast, small-bucket models attempt to integrate lot sizing and scheduling by allowing one or at most two products to be scheduled per period and to carry over the setup state from period to period. The latter, s, is achieved by an increased number of binary variables (Suerie 2005). Irrespective of the granularity of the underlying time grid, in discrete time-based lot-sizing models the start and end of production runs as well as the updates of the inventory status are restricted by the period boundaries. Clearly, the accuracy with which the time representation is modelled depends on the relative length of the time periods. In the case of a dense time grid, e.g. imposed by high production speed of the equipment, an excessively large number of decision variables and constraints are needed. Furthermore, for modelling sequence-dependent setup times and costs, an even considerably larger number of variables are necessary.

The second category of hybrid lot-sizing models combines a discrete time scale for modelling the production runs of product families and a continuous time scale for scheduling the individual product variants within a period. For this purpose, macro-periods are defined which are divided into a fixed number of non-overlapping micro-periods with variable length (Amorim et al. 2012). This modelling approach was derived from the “General Lot Sizing and Scheduling Problem (GLSP)” due to Fleischmann and Meyr (1997) and can be regarded as more realistic compared to purely discrete lot-sizing models. But still, the computational burden associated with solving real-life problem instances can be prohibitive.

In a discrete time-based lot-sizing model, particularly in a small-bucket model, a considerable but consistently ignored issue is the definition of the length of a time period. Intuitively, weeks are chosen for macro-periods and days for micro-periods. In a practical application, however, the period length must be defined based on minimum lot sizes imposed by technological conditions or by minimum customer order sizes. In a high-speed production environment, e.g. bottling of beverages, this often leads to just a few minutes needed to produce the minimum lot size while in a low-speed environment, e.g. steel production, a few hours suffice. Accordingly, the length of a time period should be defined in the order of minutes or hours depending on the particular application environment. Discrete time-based lot-sizing models in the academic literature typically cover only 2–12 periods corresponding to a time span of just a few hours or at most a full day. With a typical planning horizon of 4–12 weeks, these lot-sizing models had to be based on an extremely large number of periods to reflect the sequencing and timing of production lots. To overcome these difficulties, the use of a continuous time scale is appealing.

The third and last category of lot-sizing models uses a continuous time representation for modelling the production activities. In this regard, it also combines issues of lot sizing and scheduling in a realistic way. Motivated by the early development of continuous time-based model formulations for scheduling chemical batch operations (see Mouret et al. 2011 for a comprehensive overview), Grunow et al. (2003) developed a continuous time-based approach for scheduling production campaigns in a supply network of the chemical–pharmaceutical industry. From their model formulation, the basic block planning approach (Günther et al. 2006), was derived as a single-stage model formulation primarily for application in high-variant production systems with volatile demand. This modelling approach was coined block planning which is a common term in industry for cyclical scheduling of product variants belonging to the same product family. Applications of the block planning approach can be found in Lütke Entrup et al. (2005) for scheduling yogurt production lines, in Günther et al. (2006) for hair dye production, in Bilgen and Günther (2010) who developed an integrated model for production and distribution planning, in Farahani et al. (2012) for the production and distribution of perishable food products and in Mattik et al. (2014) for the scheduling of continuous casters and hot strip mills in the steel industry.

Irrespective of the specific representation of time, lot-sizing models are based on the same paradigm of balancing the trade-off between setup costs which are incurred whenever a production run for a product is started and inventory holding costs charged for production in advance of demand. In contrast, scheduling models usually aim at achieving time targets and avoiding delays in the completion of the production schedule. For several reasons, we found it difficult to employ conventional lot-sizing approaches for scheduling production activities in a number of industrial projects, for instance in the electronics, the consumer goods, the chemical, and the steel industry.

First, the usual assignment of setup costs and times to products does not realistically reflect the changeover processes prevalent in advanced manufacturing technology. In a great number of industrial settings, we observed that setup conditions are related to the processing mode of the production equipment rather than to individual product types. Hence, the common assignment of setup costs and times to individual products appears to be questionable since setup costs are often caused by changing the basic processing mode and not for switching between different product types. As an example, consider the bottling of beverages (see the case-based example in Sect. 5.1) where stretch blow-moulding machines are set up for a specific type of plastic bottles by mounting the required moulds into the processing head of the machine. Once the machine is set up for a specific type of bottle, a variety of beverages can be bottled with only a minor changeover between the different product types. Therefore, the definition of lot sizes should primarily refer to the retention of a basic setup condition of the production equipment instead to the production quantity of an individual item.

Principally, the following types of setup activities can be distinguished.

• In the simplest cases, setup activities are independent of the sequence of products and thus setup times and costs are associated with the setup of a single product type.

• Another type of setup activities can be referred to as family setup. In this case, the setup is accomplished for a family of related product variants with only small or no setup requirements for a changeover to another variant in the same product family. Examples are the setup of tools or electronic components in the magazine of an automated assembly machine (Yilmaz et al. 2007). This setup type is more demanding because the changeover effort between families depends on all of the predecessors.

• With limited changeover environments are described in which certain changeovers between product types are prohibited. Examples can be found in the chemical and pharmaceutical industry, where residues of the predecessor product could contaminate the succeeding product.

• A natural sequence exists when the sequence of products after a major setup is pre-defined due to technological reasons. This case, which is quite common in process industries, especially in the food and beverage industry, is considered in this paper.

• The most general case is full sequence flexibility. In this case, the sequence of products can be chosen arbitrary, but the setup effort depends on the sequence of products. In most industrial applications, a few standard types of setup operations suffice to model the sequence-dependent setup effort while in literature mostly an unrealistically wide range of setup times and costs is assumed.

Certainly combinations exist, for instance, major setups for a family of products and a natural sequence with minor setups for changing to another product variant within the same family.

Second, in many industrial applications setup costs are defined as opportunity costs to compensate for the unproductive times during the change of the setup state. This interpretation of setup costs is quite common, especially because out-of-pocket costs caused by the consumption of material or energy often play a minor role. Opportunity costs, however, depend on the utilization rate of the equipment and the profitability of the production facility. Clearly, these costs are only essential in bottleneck situations and even then impossible to measure. Despite this obvious interrelation, lot-sizing models known from the literature typically assume given values of setup costs and do not discuss the nature of setup costs though these costs greatly impact the resulting lot sizes.

Third, in supply chain management attention has shifted towards improved logistical performance (Pourakbar et al. 2009). Thus finished product inventories are merely regarded as buffers between the manufacturing and the distribution stage of the supply chain and costs for the deployment of the finished goods to the warehouses in the supply chain often dominate capital-oriented inventory holding costs. For instance, in the consumer goods industry, companies seek to turn over their inventories within 1 or 2 weeks after production. In this scenario, assuming 10 % interest rate per year and an average replenishment period of 10 days, per unit production costs increase only by 0.27 % due to capital based holding costs. This simple calculation shows that capital based inventory costs are extremely low and thus less essential in applications with fast product turnover, e.g. in the consumer goods industry or in companies which supply their customers according to the just-in-time principle.

From this discussion of basic techniques and assumptions for modelling dynamic capacitated lot sizing two conclusions can be drawn. The first is that the widely used capacitated lot-sizing models, which are based on a discrete representation of time, often do not comply with the changed business environment and the need to respond quickly to customer orders by frequently updating the production schedules. In this regard, continuous time-based lot sizing and scheduling models seem to be more appealing. The second conclusion is that minimizing total setup and holding costs is only appropriate if these costs can be determined as out-of-pocket costs directly assignable to individual product types. A possible way-out might be seen in activity-based costing which derives costs of activities from the actual use of resources (Cooper and Kaplan 1988). In the absence of “true” cost figures, minimizing the makespan, i.e. the time span needed to complete a given portfolio of demand elements and thus minimizing setup times, seems to be more appropriate. Another major advantage of the makespan objective is that production resources are freed as soon as possible so that additional not yet known customer demand can be integrated into the production schedule.

The block planning approach presented in the subsequent sections tries to overcome the difficulties associated with classic discrete time-based lot-sizing models and constitutes an attempt to integrate lot sizing and scheduling in a way that can easily be implemented in practice.

3 The block planning principle

In many industries, e.g. in the consumer goods industry, production systems usually consist of a single bottleneck stage after which final products are packed and shipped to distribution centres or individual customers. Since multiple products are produced on the same equipment, decisions have to be made on lot sizes and their timing and sequencing. By integrating several product types into a product family (a “block”) and by scheduling them block-wise in a pre-determined sequence, the complexity of the model is significantly reduced. Specifically, in process industries most often a natural sequence is given in which the various products are to be produced to minimize total changeover time and to maintain product quality standards. In the production of fruit juices, for instance, setups are sequenced from light to dark colours of a product and, finally, at the end of the sequence mix drinks are produced. Accordingly, all product types included in the pre-defined setup sequence are pooled into one setup family and scheduled as a block.

Scheduling policies which rely on a given sequence of product types within a setup family can be found in many industrial production systems. In the simplest case, called rigid block planning, the length of an entire block comprising a given sequence of products corresponds to the length of a period, e.g. a week. In this paper, a flexible block planning approach based on a mixed-integer linear (MILP) model formulation is proposed which introduces a considerable degree of flexibility for determining the length of an entire block, varying the production quantities for individual products within a block, and for scheduling the start-off and completion times of all blocks and production lots.

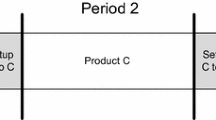
Taking a combined filling and packing line in the beverage industry as an example, the composition of a block schedule is given in Fig. 1. The line produces a specific package form, e.g. plastic bottles. Once the line is prepared after a major setup for a certain bottle type, a family of different recipes (product types) is processed in the pre-defined sequence each with a production sub-lot of variable size. When changing over from one recipe to another, a minor setup time is incurred for switching the pipelines and pre-mix tanks.

Fig. 1

Block pattern for a production line in the beverage industry

The major characteristics of the basic block planning concept upon which the development of the MILP model in Sect. 4 is based can be summarized as follows.

• Given the assignment of products to setup families, fixed setup sequences of products within a family are defined based on human expertise and technological requirements. Each block corresponds to a single setup family.

• The assignment of setup families to blocks is modelled by use of binary decision variables and determined by the optimization model based on the size and timing of demand and capacity considerations.

• The composition of blocks is not necessarily the same. Binary decision variables indicate whether a product is set up or not and continuous decision variables reflect the lot size of each product in the block. Depending on the development of demand over time, the lot sizes of an individual product may vary from block to block. As a result, also the time needed to complete a block is variable.

• The start-off and completion times of a block are not directly linked to the period boundaries but can be scheduled flexibly on the continuous time scale. Hence, a block is allowed to start as soon as the predecessor block has been completed. However, a time window can be imposed which defines the earliest possible start and the latest feasible completion time of a block.

• Typically, a major setup operation is performed before starting or after completing a block, e.g. for retooling or cleaning the manufacturing equipment, while only a minor setup operation is required when changing between products within the same block, e.g. for provision of material or for adjusting the processing conditions.

• The minimization of the makespan, i.e. the time after which the entire set of production orders is completed, can be seen as the usual objective function in short-term production scheduling. Major constraints arise from the available production capacities and the satisfaction of external demand.

• Further characteristics of the block planning approach refer to the modelling of demand in a mixed make-to-stock and make-to-order environment. For instance, in the consumer goods industry, short-term demand is known with certainty based on distinct customer orders. In addition, expected order quantities for future periods must be forecasted. The integration of both views leads to the definition of so-called demand elements, which either represent specific customer orders or forecasts. In block planning, for each demand element a due date is defined on a continuous time scale. A demand element may be filled from initial stock or by a set of assigned production orders.

As an example, Fig. 2 shows three demand elements d₁, d₂ and d₃ for a specific product assigned to due dates on the continuous time scale. The figure illustrates the possibility of satisfying these demand elements from initial stock P₀ or from a number of assigned production orders P₁, P₂ and P₃ which produce the requested product. Continuous decision variables are used to model the flow from a production order into a demand element. Moreover, Fig. 2 illustrates the possibility of indirectly considering shelf life by limiting the assignment of demand elements to only the most recent production orders, i.e. excluding assignments to blocks with early time windows or to initial stock.

Fig. 2

Assignment of demand elements to production orders and initial stock

4 Development of an optimization model

4.1 MILP model formulation

In the following, a novel MILP model for lot sizing and scheduling in a single-stage production system based on the block planning principle is presented. Such models can be formulated using a discrete or a continuous representation of time. To provide increased flexibility for scheduling the production activities in face of the large product variety and to avoid that the start and the end of production runs are confined to the period boundaries we develop a continuous time-based model formulation. As mentioned before, the sequence in which the various products are scheduled within a block is pre-defined following the human planner’s expertise and technological requirements, whereas the assignment of product families to blocks is not confined to any pre-defined setup sequence. Moreover, the model formulation is based on the following specific assumptions.

• External demand is given in the form of demand elements which are distinguished by product type, demand quantity and due date defined on a continuous time scale.

• Demand elements for the same product and the same due date are aggregated into one composite demand element.

• Each block can be executed within a pre-defined time window. The length of the time window determines the degree of flexibility inherent in the model application. Time windows may overlap.

• Blocks are numbered in consecutive order according to non-decreasing end times of the time windows.

As a flexible and practice-oriented approach, we propose that a “menu” of overlapping blocks is defined by the human planner. In the simplest case, only one block per period, e.g. per week, would be allowed. In the case of a wide range of products and high demand volatility it seems reasonable to offer a “menu” of blocks without product families being assigned to them in advance. Figure 3 displays an example of three blocks assigned for completion during overlapping time windows. Binary variables indicate whether a block should be activated, i.e. one of the available setup families should be assigned to it, or the block should be kept idle. The length of an active block is determined by the setup and manufacturing time requirements of the individual production lots.

Fig. 3

Definition of time windows

To facilitate the model formulation demand elements $k \in K$ are consecutively numbered in increasing order of due dates. The pointer $p(k)$ indicates the specific product $p \in P$ to which a demand element refers. Principally, a demand element can be satisfied from any preceding block including initial stock. However, in a practical application, the number of feasible blocks will be limited. Hence, a set $I(k)$ of preceding blocks is defined from which demand element k can be satisfied. In turn, a set $K(i)$ can be derived which defines the succeeding demand elements which can be satisfied from block i.

The notation used in the model formulation is given as follows.

4.1.1 Indices and index sets

$i \in I$ :

blocks ($i = 1, \ldots ,I^{\prime }$ )

$j \in J$ :

product families

$p \in P$ :

products

$p \in P(j)$ :

products which belong to product family j

$k \in K$ :

demand elements

$i \in I(k)$ :

set of preceding blocks from which demand element k can be satisfied

$k \in K(i)$ :

set of succeeding demand elements which can be satisfied from block i

$p(k)$ :

product to which demand element k refers

4.1.2 Parameters

$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha }_{i} ,\bar{\alpha }_{i}$ :

earliest start and latest feasible completion time, respectively, of block i

$a_{p}$ :

unit production time for product p

$s_{p}$ :

minor setup time per sub-lot of product p

$S_{j}$ :

major setup time for product family j

$d_{k}$ :

quantity of demand element k

4.1.3 Decision variables and domains

$x_{ik} \ge 0$ :

quantity of demand element k satisfied from production in block i

$y_{ij} \in \left\{ {0,1} \right\}\; = \;1,$ :

if product family j is assigned to block i (0, otherwise)

$\rho_{ip} \in \left\{ {0,1} \right\}\; = \;1,$ :

if product p is set up in block i (0, otherwise)

$\sigma_{i} \in \left\{ {0,1} \right\}\; = \;1,$ :

if block i is active, i.e. a product family is assigned to it (0, otherwise)

$\alpha_{i} \ge 0$ :

start time of block i

$\delta_{i} \ge 0$ :

duration of block i

The constraints of the block planning model are the following.

4.1.4 Setup constraints

Constraint (1) ensures that exactly one product family j∈J is assigned to each block if the block is active, i.e. $\sigma_{i} = 1$, and no product family is assigned if the block is not active, i.e. $\sigma_{i} = 0$.

$$ \sum\limits_{j \in J} {\,y_{ij} } = \sigma_{i} \quad \forall i \in I. $$

(1)

According to (2), binary setup variables $\rho_{ip}$ for the production sub-lots are allowed to take values of one only if the respective product family j is assigned to the block, i.e. $y_{ij} = 1$.

$$ \sum\limits_{p \in P(j)} {\rho_{ip} } \le y_{ij} \cdot \left| {P(j)} \right|\quad \forall i \in I,\,\,j \in J. $$

(2)

Constraint (3) models the relationship between the product flow $x_{ik}$ from block i into demand element k and the binary setup variable $\rho_{ip}$. The flow quantity is enforced to zero if no corresponding setup operation is performed, i.e. $\rho_{ip} = 0$.

$$ x_{ik} \le d_{k} \cdot \rho_{i,p(k)} \quad \forall i \in I,\,\,k \in K(i). $$

(3)

4.1.5 Block schedule

The next set of constraints is needed to model the succession of blocks. Equation (4) expresses the duration of a block which results from the major setup time for the product family assigned to the block, the minor setup times for all sub-lots and the time required for producing the sub-lot sizes. Note that $\delta_{i} = 0$ if the block is non-active. Further note that only one single product family is assigned to the block due to (1) so that variables $\rho_{ip}$ and $x_{ik}$ may take positive values only for the respective product family. Actually, variables $\delta_{i}$ are not essential since they can be replaced by the expression on the right-hand side of (4).

$$ \delta_{i} = \sum\limits_{j \in J} {S_{j} \cdot y_{ij} } + \sum\limits_{p \in P} {s_{p} \cdot \rho_{ip} + \sum\limits_{k \in K(i)} {a_{p(k)} \cdot x_{ik} } } \quad \forall i \in I. $$

(4)

According to (5), a block is allowed to start as soon as the predecessor block has been completed. Constraints (6) and (7) impose time windows with boundaries $\underline{\alpha }_{i}$ for the earliest start-off and $\bar{\alpha }_{i}$ for the latest completion time of a block. Note that in case a block is non-active, i.e. $\sigma_{i} = 0$, the respective assignment variables $y_{ij}$ and $\rho_{ip}$ and the lot size $x_{ik}$ will be enforced to zero due to (1) to (3) as well as the block duration $\delta_{i}$ in (4), meaning that no setup or production activity takes place. Moreover, in that case the lower boundary of the time window imposed in (6) will not be binding. But still, the start time of the block will take a positive value considering the finish time of the predecessor block according to constraints (5).

$$ \alpha_{i} \ge \alpha_{i - 1} + \delta_{i - 1} \quad \forall i = 2, \ldots ,I^{\prime } $$

(5)

$$ \alpha_{i} \ge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha }_{i} \cdot \sigma_{i} \quad \forall i \in I $$

(6)

$$ \alpha_{i} + \delta_{i} \le \bar{\alpha }_{i} \quad \forall i \in I. $$

(7)

4.1.6 Matching production output and demand

The following constraint is needed to allocate output from the different blocks to the demand elements. Constraint (8) makes sure that sufficient output quantities are allocated from the feasible blocks $i \in I (k )$, i.e. from those preceding the due date of demand element k, to each of the demand elements. It should be noted that index set $I (k )$ is defined such that it includes only blocks with time windows preceding the due date of demand element k.

$$ \sum\limits_{i \in I(k)} {x_{ik} } = d_{k} \quad \forall k \in K. $$

(8)

4.1.7 Objective function

The entire optimization model consists of constraints (1) to (8) and the objective function (9) stated below. The objective function aims to minimize the makespan, i.e. to complete the entire production schedule as early as possible. Indirectly, this objective minimizes setup times and thus tends to maximize the capacity utilization.

$$ { \hbox{min} }\,\,\,\alpha_{I'} + \delta_{{I^{\prime}}}. $$

(9)

It should be noted that the block planning approach is not confined to the makespan objective. Bilgen and Günther (2010) have shown how to incorporate setup and holding costs into the objective function.

4.2 Variable reduction

The extended model formulation presented in the following is based on the distinction of fixed and optional blocks. Since each product family must be scheduled at least once in the course of the planning horizon—given that a positive net-requirement for at least one item within the product family exists—we consider the setup of one block of each product family as being fixed, but still leave the start-off time of the block open. Further setups of a product family are considered optional because the number and the size of the respective blocks as well as their timing have to be determined by the optimization model. The rationale behind the introduction of fixed blocks is to reduce the number of binary decision variables for the setup of blocks and product types.

In most production systems, different types of products are produced using the same equipment. Hence, stocks are to be built up, which cover the demand between successive production runs of the same product. The development of stocks over time mirrors the stochastic demand process and is heavily affected by the short-term replenishment quantities of the customers. Moreover, stock levels are impacted by the application of the lot-sizing model under a rolling horizon regime. Once an individual product runs out of stock, a major setup activity for the entire product family, i.e. the setup of a complete block, is induced. In this case, usually production runs for various products are activated because in face of the excessive major setup times it would be uneconomic to set up the production system only for a single product.

Assume that demand elements are consolidated on a daily basis. The run-out-time of initial stock ${rot}_{p}$ of any product $p \in P$ can easily be calculated as the day at which the initial stock $F_{p0}$ is depleted:

$$ {rot}_{p} = { \hbox{min} }\left\{ {\tau \left| {\sum\limits_{\tau ' = 1}^{\tau } {e_{p\tau '} } } \right. \ge F_{p0} } \right\}\quad \forall p \in P, $$

(10)

where $\tau$ is the consecutive number of days within the planning horizon and $e_{{p\tau^{\prime } }}$ indicates the external demand of product $p \in P$ on day $\tau^{\prime }$.

The minimum of the run-out-times for items $p \in P(j)$ within a product family $j \in J$ defines the run-out-time ${ROT}_{j}$ of the respective product family.

$$ {ROT}_{j} = \mathop {\hbox{min} }\limits_{p \in P(j)} \left\{ {{\text{rot}}_{p} } \right\}\quad \forall j \in J. $$

(11)

To determine the sequence of the fixed blocks, the corresponding product families $i = 1, \ldots ,I^{\prime }$ are sorted in ascending order of their run-out-times ${ROT}_{j}$ giving ${ROT}_{1} \le {ROT}_{2} \le , \ldots ,{ROT}_{{I^{\prime } }}$. Accordingly, products included in the ordered set of product families are consecutively numbered k = 1,2,…,P. This step constitutes the first part of the production schedule consisting of a sequence of fixed blocks and respective product setups. However, lot sizes of the individual products still need to be determined by means of the optimization model.

Given the sequence of the fixed blocks and the product families included therein, initial demand elements $d_{k}$ for all products k = 1,2,…,P can be obtained as total net-demand over the time span from the beginning of the planning period until the run-out-time $ROT_{{I^{\prime } }}$ of the last of the fixed blocks. ${{ROT}}_{{I^{\prime } }}$ is also assumed as the due date of these demand elements.

$$ d_{k} = \hbox{max} \left\{ {0,\sum\limits_{{\tau \le {\text{ROT}}_{I'} }} {e_{k\tau } } - F_{k0} } \right\}\quad k = 1,2, \ldots ,P. $$

(12)

Note that each product appears only once in the first part of the schedule. Hence, product index p can be replaced by index k for the demand elements. Production lot sizes from the fixed blocks must be sufficient to satisfy initial demand elements defined this way. Nevertheless, actual lot sizes might be greater than initial demand since the point in time for the consecutive setup is not known in advance.

The second part of the production schedule contains the optional blocks, i.e. the “menu” of blocks defined by the human planner. For these blocks, it is left to the optimization model to decide on the assignment of product families to blocks, on the sub-lot sizes of the individual products and on the start and completion times of the production activities. Since not all of the allowed optional blocks must be utilized, active and non-active blocks can be distinguished. Figure 4 illustrates the composition of the entire production schedule using an example of a production schedule with three product families and five optional blocks. After one fixed block of each of the three product families is scheduled in ascending order of their run-out-times, the second part of the schedule contains five optional blocks. For non-active blocks, no setup or manufacturing activity takes place.

Fig. 4

Example of a production schedule with three product families and five optional blocks

Product families whose stocks deplete during the planning horizon require at least one setup, i.e. they are represented with one fixed block $i \in I^{fix}$ in the schedule (see Fig. 4). In constraints (13) and (14), respectively, the binary setup variables for fixed blocks and products are set to one. In addition, constraint (15) ensures that for all fixed blocks the assigned demand elements $d_{k}$ from equation (12) must be satisfied.

$$ \sigma_{i} = 1\quad \forall i \in I^{fix} $$

(13)

$$ \rho_{i,p(k)} = 1\quad \forall i \in I^{fix} ,k \in K(i) $$

(14)

$$ x_{ik} \ge d_{k} \quad \forall i \in I^{fix} ,k \in K(i). $$

(15)

For all fixed blocks $i \in I^{fix}$ constraints (13), (14) and (15) replace (1), (2) and (8) in the original model formulation and variables $y_{ij}$ can be fixed according to the pre-determined family-block assignment.

4.3 Discussion

Despite the progress that has been achieved with more realistic model formulations and advanced solution methodologies, lot sizing and scheduling is still a very challenging task due to excessive computational times. This is especially true if complex industrial conditions and a large number of entities, e.g. products or demand elements, have to be modelled. Obviously, a continuous representation of time is more adequate to model the succession of production activities compared to a discrete time scale which is common in classical lot sizing. See, for instance, Shaik et al. (2006) who compare different model formulations for application in the chemical industry. Jordan and Drexl (1998) showed the equivalence between the discrete lot sizing and scheduling and the continuous batch sequencing problem for the single-machine case with sequence-dependent setup times and cost. In their numerical experiments, they demonstrated the superiority of the batch sequencing approach in terms of CPU time. But still, the discrete time representation is the predominant modelling technique in the OR-related literature.

Obviously, the size of the discrete time scale models depends on the number of products and periods. In a very elementary production setting with P = 10 products and T = 12 periods (weeks) and under the most rigid big-bucket modelling assumptions, i.e. multiple products scheduled per period, already 240 decision variables for modelling the production and inventory quantities and 120 additional binary variables for setup activities are required. Extending the modelling assumptions to a small-bucket model with seven micro-periods per week, the number of continuous variables increases to 1680 and, because of the additional binary variables for modelling the setup state, the same number of binary variables is needed. Small-bucket models of this size are extremely hard or impossible to solve using standard optimization software.

For illustration, a specific example is taken from the beverage industry (see the case-based example in Sect. 5.1). Today, powerful filling machines are used which operate at a speed of 300 l/min, thus allowing one Euro pallet containing 750 l to be produced within 2.5 min. Given minimum customer order sizes of one pallet, the appropriate length of a micro period would be 2.5 min leading to a total number of 4,838,400 decision variables each for production, inventory, setup activities and setup states, based on a typical planning horizon of 12 weeks and 100 products and continuous plant operation (24 h per day and 7 days a week). Half of these decision variables are binary. The size of the resulting optimization problems is far beyond the scale of problem instances that can be solved today even with the most powerful standard optimization solvers.

These estimations of the model size clearly show that conventional discrete time-based model formulations are at best useful in applications with low-speed production technology, aggregate demand for a limited number of products, and a small number of big-bucket periods. For calculating the size of the block planning model presented in Sect. 4.1, let K indicate the number of demand elements, B the number of blocks, W the number of blocks from which a demand element can be filled (the size of the time window), J the number of product families and $\bar{P}$ the average number of product types per family. Then the number of continuous variables can be expressed as $K \cdot W + B$ (not counting the redundant variables defined in (4)). In addition, $B \cdot \left( {J + J \cdot \bar{P} + 1} \right)$ binary variables are needed. The number of constraints amounts to $B \cdot \left( {J + 3} \right) + K \cdot W - 1$ (not counting the redundant constraints (4) and the lower bounds defined in (6)). For instance, K = 1,000, B = 24, W = 4, J = 8, and $\bar{P} = 7.5$ are realistic dimensions of real-life instances in the beverage industry. Based on these values, the block planning model contains 4,024 continuous and 1,656 binary variables and 4,263 constraints. As it is shown in the numerical investigation presented in the next section, the resulting optimization models are easily tractable by use of standard optimization packages.

In a real application, planners have to decide whether demand elements can be aggregated so that the number of continuous variables and constraints is greatly reduced. Clearly, if single customer orders are considered as demand elements, numerous continuous decision variables are needed. As for the binary variables, which primarily determine the CPU time requirements, their number depends on the range of blocks and products and is independent of the demand granularity.

A particular difficulty with continuous lot sizing is the modelling of inventory quantities and related storage capacity constraints. In contrast to discrete lot-sizing models, the timing of stock receipts is variable and not confined to period boundaries. However, Bilgen and Günther (2010) have shown that stock receipts can be modelled by introducing an auxiliary time grid and by use of additional binary variables which indicate whether a production activity is completed up to a particular point in time. In this way, inventory states and transhipment quantities can be incorporated into the model formulation.

Finally, it should be remarked that the block planning model is also applicable if no pre-defined setup sequence of products within a family exists. In this case, each product must be defined as its own “family”. In contrast, incorporating a pre-defined setup sequence into a discrete time-based lot-sizing model entails a very elaborate procedure using a sequence-dependent model formulation and the definition of prohibitively high setup costs or times for infeasible product sequences.

5 Numerical investigation

Based on a case-based example from the beverage industry numerical experiments are conducted to examine the practical applicability of the proposed block planning approach for production systems with a single bottleneck stage. In particular, it is shown that optimal solutions to problems of realistic size can be obtained within reasonable CPU time. Please note that it is not the aim of this section to go into details of beverage production (Ferreira et al. 2009; Bilgen and Günther 2010; Ferreira et al. 2012), but merely to obtain a realistic test bed for the numerical experiments.

5.1 A case-based example from the beverage industry

As a practical case, the production of beverages at a leading European producer of fruit juice is considered. The beverages as well as other branches of the consumer goods industry face an increased number of package forms, customized package prints and labels, and a variety of flavours and compositions of ingredients. Caused by environmental regulations and the need for improved logistics efficiency, novel package forms have been developed. For instance, in the European Union plastic bottles represent the major package form for fruit juices and other types of refreshment drinks. At the same time, glass bottles become less important except for alcoholic drinks and some specific kinds of beverages. Another common package form is carton boxes made from foldable cardboard. However, carton boxes continue losing market share compared to plastic bottles. Both plastic bottles and carton boxes allow liquid food to be packaged and stored under ambient temperature conditions for up to a year.

Specifically in the production of beverages, combined bottling and packaging lines are established for each package form, e.g. plastic bottles, carton boxes, and glass bottles. A line usually produces a number of product types, e.g. juices of different flavour, and fills them into individual units for use by end customers. Each product type, e.g. orange or pineapple juice, corresponds to a specific recipe which determines the ingredients and the processing conditions of the product. Figure 5 illustrates the typical product-line assignment.

Fig. 5

Product-line assignment in beverage production

Due to the large effort for changing over between different package forms on a line, manufacturers in the beverage industry pursue a production policy with fairly large run times for a given package form. However, to cope with the increased product variety short production cycles for product types and frequent changeovers between products within the same product family are common. Typically, production lines are set up for a specific package form requiring a major setup such that the changeover between the individual product types can be accomplished with only a minor setup operation for switching the pipelines which connect the pre-mix tanks with the filling lines.

In many industrial production settings, e.g. in the beverage industry, setup conditions are considerably complex and the assignment of setup costs and times to a specific product may become a difficult task. As an example, consider blow-moulding machines which represent the recent technology for bottling of beverages like mineral water or fruit juices. This kind of machinery is set up for a specific shape and size of plastic bottles by mounting the required moulds into the processing head of the machine. The actual plastic bottles are formed on the machine from compact pre-forms through thermal and high-air pressure processes. Depending on the configuration of the machine, around 20 moulding devices are arranged on a rotary turret thus allowing a respective number of bottles to be produced on the fly. Due to the high-pressure filling capabilities of the machine, 15–20,000 plastic bottles of one-litre size can be filled per hour. Auxiliary equipment for bottle washing, capping and labelling is integrated into the line as well as packaging machines for the generation of unit loads used in retail stores or transportation. Once the line is set up for a specific type of bottle, a variety of beverages can be filled with only a minor changeover between the different product types.

Also inventory holding costs have to be reconsidered in the context of supply networks with intensive material flows and short-term delivery requests from customers to be found in the consumer goods industry. Traditionally, holding costs are defined to compensate for the interest of capital tied up in inventory. In practice, however, production managers face difficulties in defining these costs as out-of-pocket costs since no clear relationship between cash flows and individual production activities can be identified and the turnover periods of stocks have considerably decreased. Therefore, in industries with high inventory turnover minimizing stock levels is typically seen as a secondary goal while serving customer requests on time and improving logistics performance are of paramount importance.

5.2 Experimental design

The major parameter settings in our numerical experiments were derived from the industrial application example in the previous subsection. Specifically, the definition of product families and the sequencing conditions for product types within a family, the bottling and packaging technology, and the generation of demand elements reflect key issues of this real-life application. Further assumptions and basic parameter settings of the lot sizing and scheduling problem at hand are as follows.

• The planning horizon comprises 12 weeks and the plant is operated 24 h per day and 7 days a week.

• From the various package forms, the line for filling plastic bottles is considered as the one showing the highest filling speed and the most complex setup conditions. As mentioned before, lines are dedicated to package forms, e.g. plastic bottles or carton boxes, and thus the lot sizing and scheduling problem can be solved separately for each line.

• Major and minor setup times being typical for stretch blow-moulding machines, which represent the latest technology for processing plastic bottles, are assumed.

• On the considered bottling and filling line eight different types of plastic bottles (product families) are produced.

• The number of product types per family is randomly generated from the uniform distribution $U\left[ {5,10} \right]$ rounded up to the nearest integer giving 8 product types per family on average.

• Depending on the relative demand volume, we distinguish between high, medium and low-runner products. An equal number of product types is randomly assigned to these categories.

While certain types of soft drinks show a strong seasonal demand pattern, the consumption of fruit juice is only slightly affected by seasonal factors. Hence, in the generation of the demand elements we do not consider any seasonality. Instead, we assume capacity load scenarios of 75 and 90 %, respectively, which reflect conditions of low and high average workload. Moreover, since demand in the fast moving consumer goods industry is characterized by a large variety of customer order sizes and irregular replenishment times, we investigate three demand scenarios which differ by the average time between orders. Accordingly, a parameter f = 1, 3, 7 is introduced which expresses demand frequency, i.e. the average interval (in days) between the occurrence of demand elements. In our experiments, f = 1 indicates daily demand, f = 3 demand occurring every third day, and f = 7 demand occurring once per week. The size of the demand elements is adjusted accordingly so that in each of the scenarios the same total demand volume over the planning horizon is observed.

The random generation of demand elements can be described by the following procedure.

5.2.1 Determination of the number of demand elements

• (a) To reflect the cyclical production mode and the corresponding development of inventories, it is assumed that sufficient initial stocks of all products exist. Hence, no demand is assigned to an initial time interval and the first feasible demand-day $DD_{j}$ for product families $j = 1, \ldots ,8$ is determined as $DD_{j} = 2 + j \cdot 4 + \varDelta {}_{j}$ where $\varDelta_{j}$ takes values of 0, 1, and 2 with equal probability. Accordingly, ${\text{TW}}_{j} = \left\{ {S_{j} ,84} \right\}$ is assumed as the feasible time window for the assignment of demand elements of products within family j over the planning horizon of 84 days.

• (b) With 84 days planning horizon and 60 products on average, 84.6 = 5040 product-demand combinations result. Excluding the $20 \cdot 60 = 1200$ combinations with zero demand due to sufficient initial stocks from (a) above, effectively N = 5040 − 1200 = 3840 demand elements (product-demand combinations) are considered. With f representing the demand frequency factor for distinguishing between low, medium and high demand frequency, the average number of generated demand elements is determined as n(f) = N/f giving a total of n(1) = 3840, n(3) = 1280, and n(7) = 549 demand elements on average generated in the three demand frequency scenarios with f = 1, 3, and 7, respectively.

5.2.2 Determination of demand quantities

• (a) Determine $X = 24 \cdot 7 \cdot 12 = 2016$ as the total number of operating hours available based on 24 h operating time per day, seven workdays per week, and a planning horizon of 12 weeks. Considering an average workload of 75 % and 90 %, respectively, and a capacity loss of 576 h due to setup operations (giving $X - 576 = 1440$), determine Y as the effective total workload on the production system: $Y = 0.75 \cdot \left( {X - 576} \right) = 1080$ and $Y = 0.9 \cdot \left( {X - 576} \right) = 1296$, respectively.

• (b) The average size of demand elements is set to D(f)=Y/n(f) hours depending on f = 1, 3, 7 for the individual demand frequency scenarios. To create a realistic degree of demand variability, values of demand elements d(f) are randomly drawn from the uniform distribution $d(f) \in U[0.5 \cdot D(f),\,\,1.5 \cdot D(f)]$. Select randomly one of the product families and one product within the family. If the selected product is a high-runner, demand is increased by 2/3, i.e. $d(f) \leftarrow d(f) \cdot (5/3)$. If the selected product is a low-runner, demand is reduced to one-third, i.e. $d(f) \leftarrow d(f)/3$. Otherwise, demand is not changed. The detailed assignment of demand elements to due dates within the feasible time window [defined in Step 1 (a)] is accomplished as follows:

  • High demand frequency scenario (f = 1): One demand element is assigned to each day $t \in TW_{j}$.

  • Medium and low demand frequency scenarios (f = 3 and f = 7): Demand elements are randomly assigned to periods $t \in TW_{j}$ until the number of demand elements determined in Step 1 (b) is reached. Note that in case a demand element for the chosen product-period combination has already been assigned, the assignment is rejected and a new product-period combination is drawn.

• (c) The size of the demand elements is normalized using the factor Y/Z where Z indicates the total workload of the generated demand elements. This way a workload of exactly Y hours is assured.

5.2.3 Determination of blocks

• (a) For each of the product families, one fixed block is assumed. As due date, day $DD_{j} + 1$ determined in Step 1 (a) is defined.

• (b) In addition, 24 optional blocks are defined to which no specific product family is assigned in advance. The time window for the execution of the optional blocks is set such that the latest feasible completion time of blocks is evenly spread over the time interval between the completion time of the last fixed block and the end of the planning horizon. No specific lower limit for the start of a block is imposed.

5.2.4 Implementation

With two workload scenarios of 75 and 90 %, respectively, and the three levels of demand frequency, six different scenarios are investigated. Each experiment is repeated five times with different seeds of the random number generator. Detailed parameter settings are summarized in Table 1. The proposed optimization model was implemented on a PC with Dual Xeon Quad Core 2.5 GHz processor and 4 GB RAM using ILOG’s OPL Studio 6.1.1 as the modelling environment and CPLEX 11.2.1 as solver. As termination criterion, the relative MIP gap was set to 1 % throughout the experiments.

Table 1 Model parameters

5.3 Numerical results

The main goal of the numerical investigation is to examine whether the proposed block planning approach provides a practical tool for decision support in real applications, i.e. solutions to the MILP model presented in Sect. 4 are obtained within reasonable CPU time. In addition, the effect of the demand frequency is investigated. Finally, it will be shown that CPU times can be drastically reduced if demand over the final 6 weeks of the planning horizon is aggregated from daily into weekly figures.

Tables 2 and 3 show the computational performance parameters for the two scenarios of 75 and 90 % capacity load, respectively, and for different levels of demand frequency. First, it appears that the optimum makespan is only slightly affected by the different demand frequencies. Obviously, the MILP-based block planning approach is effective in combining the demand elements into blocks which are produced under the same major equipment setup. Because of the makespan objective, idle times of the production line are shifted to the end of the planning horizon allowing the planner to integrate not yet known customer demand into the schedule. This type of compact schedules is particularly preferred in food production where intermediate idle times require additional cleaning of the equipment to prevent contamination. The second observation is that the number of blocks as well as the number of sub-lots per block (product types actually produced in a block) also show a slightly decreasing tendency with increasing demand frequency in both capacity load scenarios, i.e. fewer sub-lots are set up when demand elements occur less frequently. Finally, it is observed that in both capacity load scenarios CPU times are extremely moderate. Though CPU times are considerably higher in the 90 % capacity load scenario, in particular in the case of high demand frequency, they are still at a very low level considering the application environment of operative planning over a 12-week horizon. Apparently, CPU times decrease with a smaller number of demand elements due to the decrease in model size and they increase with a higher capacity load. The final column of Tables 2 and 3 shows the MIP gap achieved when the optimization run terminated. Though a 1 % MIP gap was imposed as termination criterion, the actual MIP gap was well below this threshold.

Table 2 Computational performance of the MILP model under the 75 % capacity load scenario (average over five replications)

Table 3 Computational performance of the MILP model under the 90 % capacity load scenario (average over five replications)

A related set of experiments was conducted to investigate the effect of demand aggregation. Due to uncertainty in customer release quantities and replenishment times, it is merely impractical in most branches of the consumer goods industry to determine precise hourly or daily production schedules for more than a few weeks ahead. Hence, we aggregated the demand elements for the final 6 weeks of the 12-week planning horizon from daily into weekly demand figures and solved the corresponding MILP model which was considerably reduced in size compared to the original model. This kind of demand aggregation seems to be appealing because it still allows the production manager to develop the associated labor schedules and procurement plans with adequate accuracy. Results indicated in Tables 4 and 5 reveal that in all test cases the CPU time falls well below one second. At the same time, the differences in makespan compared to the original model are only minor. As can be seen from Tables 4 and 5, the applied demand aggregation leads to a slight decrease in the average number of blocks and a slight increase in the average number of sub-lots per block. In fact, aggregate demand figures provide additional freedom in creating larger production lots and thus saving one or the other setup operation.

Table 4 Computational performance of the aggregate MILP model under the 75 % capacity load scenario (average over five replications)

Table 5 Computational performance of the aggregate MILP model under the 90 % capacity load scenario (average over five replications)

6 Conclusions

In this paper, an MILP-based block planning concept has been presented that is intended for practical application in production systems which are characterized by a single bottleneck stage and high demand volatility. Such production systems can be found, for instance, in the consumer goods as well as in the chemical industry. In these process-related industries, planners are confronted with a variety of product specifications which are produced on the same manufacturing equipment by adjusting process parameters, such as process duration and processing mode or the mix of raw materials. To illustrate the practical applicability of the block planning concept, the production of beverages was considered as a case-based example. It could be shown that the proposed MILP modelling approach adequately reflects the relevant practical issues and problem instances reflecting realistic conditions could be solved in very short computational time by use of standard optimization software.

Generally, the problem of determining production order sizes, their timing and sequencing with setup considerations is equivalent to a capacitated lot size problem. However, the change in business conditions as shown by shortened replenishment lead times, increased product variety, high-speed production equipment with more complex setup conditions, increased inventory turnover etc. calls for a change of paradigm. It appears that the industrial relevance of traditional lot sizing and scheduling models has shifted from discrete parts manufacturing to process industries, particularly, for applications with long processing times of campaigns in multi-stage production systems. Hence, it is more relevant in the multi-plant supply network planning stage than in detailed short-term scheduling of operations. In addition, in the chemical industry setup costs are often easier to determine in the form of direct costs mainly when after a product changeover output is temporarily produced, which does not meet the desired specifications (Chapter 5 of Schöpperl 2013), or excessive clean-out times occur as in the pharmaceutical industry.

The block planning approach proposed in this paper relies on a continuous representation of time which makes it unnecessary to use binary variables for the product-period assignments and the changeovers as in capacitated discrete time-based lot-sizing models. Moreover, the block planning approach reflects practical issues like the definition of setup families with consideration of major and minor setup times in a realistic way.

As objective function, the minimization of makespan was pursued. The resulting setup time savings are specifically appealing in situations where direct setup costs are less essential and the actual setup time consists of downtime of the production equipment. Another condition that justifies the use of the makespan objective is the increased inventory turnover, specifically in the consumer goods industry, which makes the common understanding of inventory holding costs questionable. In any case, the framework of linear programming is flexible enough to incorporate alternate objective functions or specific conditions arising in the individual industrial application.