Abstract
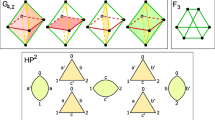
For an effective action of a compact torus T on a smooth compact manifold X with nonempty finite set of fixed points, the number \(\frac{1}{2}\dim X-\dim T\) is called the complexity of the action. In this paper, we study certain examples of torus actions of complexity one and describe their orbit spaces. We prove that \({\mathbb {H}}P^2/T^3\cong S^5\) and \(S^6/T^2\cong S^4\), for the homogeneous spaces \({\mathbb {H}}P^2={{\,\mathrm{Sp}\,}}(3)/({{\,\mathrm{Sp}\,}}(2)\times {{\,\mathrm{Sp}\,}}(1))\) and \(S^6=G_2/{{\,\mathrm{SU}\,}}(3)\). Here, the maximal tori of the corresponding Lie groups \({{\,\mathrm{Sp}\,}}(3)\) and \(G_2\) act on the homogeneous spaces from the left. Next we consider the quaternionic analogues of smooth toric surfaces: they give a class of eight-dimensional manifolds with the action of \(T^3\). This class generalizes \({\mathbb {H}}P^2\). We prove that their orbit spaces are homeomorphic to \(S^5\) as well. We link this result to Kuiper–Massey theorem and its generalizations studied by Arnold.






Similar content being viewed by others
Notes
We assume that all cohomology rings are taken with \({\mathbb {Z}}\) coefficients unless stated otherwise.
In some sources, the term spectrohedron denotes an intersection of the cone \(C_n\) with a plane of any dimension, not just hyperplanes.
It is convenient to have two different symbols for the same object.
At this point, we essentially use the fact that the quotient map from a quasitoric manifold to its orbit space admits a section.
References
Arnold, V.I.: Relatives of the quotient of the complex projective plane by complex conjugation. Proc Steklov Inst. Math. 224, 46–56 (1999)
Atiyah, M., Berndt, J.: Projective planes, Severi varieties and spheres. In: Surveys in Differential Geometry VIII, Papers in Honor of Calabi, Lawson. Siu and Uhlenbeck 1–27 (2003)
Ayzenberg, A.: Space of isospectral periodic tridiagonal matrices. Algebraic Geom. Topol. Preprint arXiv:1803.11433
Ayzenberg, A.: Torus actions of complexity one and their local properties. Proc. Steklov Inst. Math. 302(1), 16–32 (2018)
Buchstaber, V.M., Panov, T.E., Ray, N.: Spaces of polytopes and cobordism of quasitoric manifolds. Moscow Math. J. 7(2), 219–242 (2007)
Buchstaber, V.M., Terzić), S.: (2n, k)-manifolds and applications. In: Mathematisches Forschung Institut Oberwolfach, Report No. 27/2014, p. 58 (2014)
Buchstaber, V.M., Terzić, S.: Topology and geometry of the canonical action of \(T^4\) on the complex Grassmannian \(G_{4,2}\) and the complex projective space \({\mathbb{C}}P^5\). Moscow Math. J. 16(2), 237–273 (2016)
Buchstaber, V.M., Terzić, S.: The foundations of (2n, k)-manifolds. Mat. Sb. 210(4), 42–86 (2019)
Choi, S., Park, H.: Small covers over wedges of polygons. J. Math. Soc. Japan 71(3), 739–764 (2019)
Davis, M., Januszkiewicz, T.: Convex polytopes, Coxeter orbifolds and torus actions. Duke Math. J. 62(2), 417–451 (1991)
Finashin, S.M.: Differential topology of quotients of complex surfaces by complex conjugation. J. Math. Sci. 91(6), 3472–3475 (1998)
Goresky, M., Kottwitz, R., MacPherson, R.: Equivariant cohomology, Koszul duality, and the localization theorem. Invent. Math. 131, 25–83 (1998)
Gugnin, D.: Branched coverings of manifolds and nH-spaces. Funct. Anal. Appl. 53(2), 68–71 (2019)
Hopkinson, J.F.L.: Quoric manifolds. A thesis submitted to the University of Manchester for the degree of Doctor of Philosophy in the Faculty of Engineering and Physical Sciences
Karshon, Y., Tolman, S.: Topology of complexity one quotients. Preprint arXiv:1810.01026v1
Kirwan, F.C.: Cohomology of Quotients in Symplectic and Algebraic Geometry, Mathematical Notes, 31. Princeton University Press, Princeton (1984)
Kuiper, N.: The quotient space of \({\mathbb{C}}P^2\) by the complex conjugation is the 4-sphere. Math. Ann. 208, 175–177 (1974)
Kuroki, S.: Classifications of homogeneous complexity one GKM manifolds and GKM graphs with symmetric group actions. RIMS Kokyuroku 1922, 135–146 (2014)
Massey, W.: The quotient space of the complex projective plane under the conjugation is a 4-sphere. Geom. Dedic. 371–374 (1973)
Masuda, M., Panov, T.: On the cohomology of torus manifolds. Osaka J. Math. 43, 711–746 (2006)
Orlik, P., Raymond, F.: Actions of the torus on 4-manifolds. Trans. AMS 152(2), 531–559 (1970)
Sarkar, S., Stanley, D.: Cohomology Rings of a Class of Torus Manifolds. Preprint arXiv:1807.03830)
Acknowledgements
I am grateful to Shintaro Kuroki, who asked the question about the \(T^3\)-orbit space of \({\mathbb {H}}P^2\), motivating this work. I thank Victor Buchstaber and Nigel Ray, from whom I knew about Jeremy Hopkinson’s work on quaternionic toric topology. I also thank Mikhail Tyomkin for bringing the paper of Atiyah and Berndt on octonionic projective plane to my attention. The author thanks the referee for the remarks which helped to improve the exposition of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The article was prepared within the framework of the HSE University Basic Research Program.
Rights and permissions
About this article
Cite this article
Ayzenberg, A. Torus Action on Quaternionic Projective Plane and Related Spaces. Arnold Math J. 7, 243–266 (2021). https://doi.org/10.1007/s40598-020-00166-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40598-020-00166-4