Graph lattice: random walk and combinatorial identities

Abstract

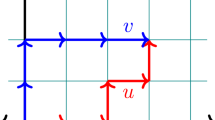
Graph lattice has vertices at points with non-negative integer coordinates. From each vertex we have two edges: horizontal and vertical neighboring vertices (right and top). In this paper, we considered the problem of random walk on the vertices of the graph lattice without limitation on the reachability and with two types of limitations on reachability—mixed and magnetic. The set of edges of the graph with mixed reachability U is a union of disjoint non-empty sets $U_R$ and $U_Z$. Permitted path on the graph with mixed reachability is the path wherein the edges from the set $U_Z$ are thinned by the edges from the set $U_R$, i.e. the edges from the set $U_Z$ on the path are not adjacent. As a consequence of the consideration of this problem, we have obtained new proof of some combinatorial identities.