Skip to main content
SpringerLink
Log in

Numerical simulation of the flow characteristics around and through multiple porous particles

  • Published:
Computational Particle Mechanics Aims and scope Submit manuscript

Abstract

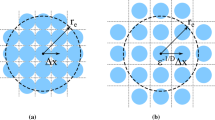
Particle–fluid and particle–particle interactions can be widely seen in lots of natural and industrial processes. In order to understand these interactions, two-dimensional fluid flowing around and through nine porous particles was studied in this paper based on the lattice Boltzmann method due to its simplicity. Uniform spatial distribution and random spatial distribution were considered and the effects of Reynold number (Re), Darcy number (Da), and the distance between the particles (dx and dy) on the flow characteristics were analyzed in detail. The investigated ranges of the parameters were 10 ≤ Re ≤ 40, 10–6 ≤ Da ≤ 10–2, D ≤ dx ≤ 4D and D ≤ dy ≤ 4D (D is the diameter of the particles). For uniform spatial distribution, it is observed that when dx(dy) increases, the interactions between the particles become weak and the fluid can flow into the spacing between the particles. Besides, the average drag coefficient (CDave) increases with dx(dy) increasing at Re = 20 and the increase rate gradually slows down. Furthermore, the distance change in the direction vertical to inflow direction has more obvious impact on the average drag coefficient. For example, for Re = 20 and Da = 10–4, when dx equals D and dy increases from 2D to 3D, CDave increases by 5.79%; when dy equals D and dx increases from 2D to 3D, CDave increases by 2.61%.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

References

  1. Chen RC, Wu JL (2000) The flow characteristics between two interactive spheres. Chem Eng Sci 55(6):1143–1158

    Article  Google Scholar 

  2. Tritton DJ (1959) Experiments on the flow past a circular cylinder at low Reynolds numbers. J Fluid Mech 6(4):547–567

    Article  MATH  Google Scholar 

  3. Bhattacharyya S, Dhinakaran S, Khalili A (2006) Fluid motion around and through a porous cylinder. Chem Eng Sci 61(13):4451–4461

    Article  Google Scholar 

  4. Dalman MT, Merkin JH, McGreavy C (1986) Fluid flow and heat transfer past two spheres in a cylindrical tube. Comput Fluids 14(3):267–281

    Article  Google Scholar 

  5. Folkersma R, Stein HN, van de Vosse FN (2000) Hydrodynamic interactions between two identical spheres held fixed side by side against a uniform stream directed perpendicular to the line connecting the spheres’ centres. Int J Multiph Flow 26(5):877–887

    Article  MATH  Google Scholar 

  6. He X, Doolen G (1997) Lattice Boltzmann method on curvilinear coordinates system: flow around a circular cylinder. J Comput Phys 134(2):306–315

    Article  MATH  Google Scholar 

  7. Hsu JP, Yeh SJ (2009) Translation of two rigid spheres perpendicular to their line-of-centers and normal to a plate. Powder Technol 194(1–2):10–17

    Article  Google Scholar 

  8. Jin H et al (2019) Numerical investigation on drag coefficient and flow characteristics of two biomass spherical particles in supercritical water. Renew Energy 138:11–17

    Article  Google Scholar 

  9. Niu XD et al (2006) A momentum exchange-based immersed boundary-lattice Boltzmann method for simulating incompressible viscous flows. Phys Lett A 354(3):173–182

    Article  MathSciNet  MATH  Google Scholar 

  10. Yu P et al (2011) Steady flow around and through a permeable circular cylinder. Comput Fluids 42(1):1–12

    Article  MathSciNet  MATH  Google Scholar 

  11. O’Brien TJ, Syamlal M (1993) Particle cluster effects in the numerical simulation of a circulating fluidized bed. In: Avidan A (ed) Circulating fluidized bed technology IV, Hidden Valley, 1993. AIChE, New York, pp 345–350

    Google Scholar 

  12. Sandeep KP, Zuritz CA (1996) Drag on multiple sphere assemblies suspended in non-newtonian tube flow. Blackwell Publishing Ltd, Oxford, pp 171–183

    Google Scholar 

  13. Beetstra R, van der Hoef MA, Kuipers JAM (2006) A lattice-Boltzmann simulation study of the drag coefficient of clusters of spheres. Comput Fluids 35(8–9):966–970

    Article  MATH  Google Scholar 

  14. Shah MT et al (2013) Effect of a cluster on gas–solid drag from lattice Boltzmann simulations. Chem Eng Sci 102:365–372

    Article  Google Scholar 

  15. Wei X, Weber J, Breault RW (2021) Numerical investigation of the penetrating gas flow into particle clusters for circulating fluidized beds. Powder Technol 388:442–449

    Article  Google Scholar 

  16. Rong FM et al (2011) Numerical simulation of the flow around a porous covering square cylinder in a channel via lattice Boltzmann method. Int J Numer Meth Fluids 65(10):1217–1230

    Article  Google Scholar 

  17. Tang Y, Liu H (2017) Modeling multidimensional and multispecies biofilms in porous media. Biotechnol Bioeng 114(8):1679–1687

    Article  Google Scholar 

  18. Nithiarasu P, Seetharamu KN, Sundararajan T (1997) Natural convective heat transfer in a fluid saturated variable porosity medium. Int J Heat Mass Transf 40(16):3955–3967

    Article  MATH  Google Scholar 

  19. Wang L et al (2015) Volume-averaged macroscopic equation for fluid flow in moving porous media. Int J Heat Mass Transf 82:357–368

    Article  Google Scholar 

  20. Qian YH, d’humières D, Lallemand P (1992) Lattice BGK models for Navier-Stokes equation. Europhys Lett 6(17):479–484

    Article  MATH  Google Scholar 

  21. Nield DA, Bejan A (2006) Convection in porous media

  22. Ladd AJC (1994) Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J Fluid Mech 271:285–309

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (51922086).

Author information

Authors and Affiliations

  1. State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an, 710049, Shaanxi, People’s Republic of China

    Mingyue Zhang, Hui Jin & Shaohua Shen

Authors
  1. Mingyue Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hui Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shaohua Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shaohua Shen.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, M., Jin, H. & Shen, S. Numerical simulation of the flow characteristics around and through multiple porous particles. Comp. Part. Mech. 10, 519–531 (2023). https://doi.org/10.1007/s40571-022-00482-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40571-022-00482-w

Keywords

Search

Navigation