1 Introduction

The fragmentation of biomass pellets and the generation of fines and dust during transport and storage have inflicted several problems in handling steps and operational units [1]. Equipment fouling, increased risk of fire, dust inhalation problems, and environmental issues are the consequences of existing fines and dust inside the bulk materials [2]. Biomass pellets are mostly transported on a large scale (ten thousand tons per hour) resulting in high-impact forces during transportation and handling [3]. The potential of fines and dust generation is highly linked to the mechanical strength of materials. The mechanical strength of biomass pellets could be measured individually or in bulk [4].

The individual mechanical strength assessment methods are conducted either by compression or impact tests. In a typical compression test, a single pellet is placed between two anvils of a compression device that compress the pellet while recording the force–displacement data. Then the stress–strain curve and the modulus of elasticity are calculated from the data. In a typical impact test, a single pellet is dropped from a known height to a plate of known material and the number of fines, and the number of pieces split from the original pellet is recorded. The bulk strength is typically measured using durability testers such as tumbling can, ligno tester, and Holmen durability tester. These devices enable pellets to collide with each other and with the walls to mimic the transportation and handling conditions by use of an air stream or rotating the device.

Research on handling and storage properties of biomass pellets has been recently taken into consideration by some researchers [5,6,7,8,9]. They highlighted the effect of transportation and handling systems on the number of generating fines. Bradley [6] pointed out that the transfer chutes are the main cause of the pellet breakage and fines generation during the handling process. Ilic et al. [7] claimed there are up to 25 wt% fines particles smaller than 3.15 mm in the biomass pellet plants while the expected amount in the equipment design process is around 5–8 wt%.

Recently, the use of numerical methods to predict the bulk flow materials has attracted attention [10]. Discrete element method (DEM) is proven as a powerful tool with the capabilities of monitoring the behavior of individual particles inside a system resulting in understanding the bulk material behavior. Recently, researchers applied DEM to study the flow properties of cylindrical pellets [11], mixing and transportation of wood pellets [12], and durability characteristics of biomass pellets [13]; however, fragmentation of biomass pellets have been scarcely investigated by modeling and simulations. A recent study addresses the modeling of deformation and breakage behavior of biofuels wood pellets [14] using the finite element method (FEM). However, due to the inherent nature of FEM, the particle–particle contacts which are crucial in breakage behavior and fines generation is missing in the model.

The objective of this paper is first to characterize the individual pellet strength of different types of biomass under uniaxial and diametrical compressions and second, to present a calibrated DEM model capable of predicting biomass breakage patterns during compression tests capable of tracking the behavior of each individual particle. The model can be used for future research on pellet fragmentation, equipment design, and to set new standards for transportation, storage, and handling of biomass pellets.

2 Materials

Two different non-torrefied and five different torrefied biomass pellets were used in this study. The origin, ultimate, and proximate analysis of the samples are given in Table 1. The moisture content and ash content of the torrefied mixed wood pellets were determined according to EN standard 14774-2 [15] and EN standard 14775 [16], respectively. The volatile matter of torrefied mixed wood pellets was measured using the method described in [17]. The proximate analysis of the rest of the samples was taken from [18]. The amount of fixed carbon was calculated by the difference of one hundred to the summation of ash, moisture, and volatile matters. There is no detailed information about the densification processes of the pellets; however, it is known that all Ash wood pellets and all Spruce wood pellets were densified in similar densification processes.

Table 1 Production properties and the proximate analysis of pellets
Full size table

3 Methods

3.1 Experimental

3.1.1 Pellet density

The pellet densities were measured based on the volume and the mass of individual pellets. In order to get the most accurate volume, pellets were polished in both ends using sandpaper. Then the pellet length and diameter were measured according to the EN standard 16127 [19]. Mass of each pellet was measured using a laboratory balance with readability down to 0.001 g. The pellet density measurement was repeated five times per sample; then, the mean values and the standard deviations were reported.

3.1.2 Compression tests

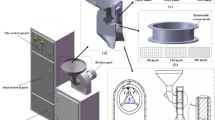
The biomass pellet strength under compression is mostly measured in two different configurations including the unconfined uniaxial and diametrical compressions (Fig. 1) [20]. The diametrical compression test is also known as Brazilian tensile strength. All the experiments in this study were carried out using an Instron compression device (Instron 5500R) using a 10 kN load cell. Pellets were placed on the lower plate of the device, which gradually compressed upward with a compression rate of 1 mm min− 1.

Fig. 1
figure 1

Unconfined uniaxial (a) and diametrical (b) compression tests adapted from [20]

Full size image

For the uniaxial tests, each pellet was polished in both ends using sandpaper in order to vertically stand on the plate and to ensure that the compressive force applies evenly to both end surfaces of the pellet. For diametrical compressions, pellets were placed on the lower plate lengthwise. The force–displacement data were recorded for each test from the beginning until a 20% drop in the force value after failure. The stress and strain values were calculated using Eqs. (1) and (2) for uniaxial compression and Eqs. (3) and (4) for diametrical compressions, respectively.

$${\sigma }_{a}=\frac{F}{{\pi r}^{2}}$$
(1)
$${\epsilon}_{a}=\frac{{l}_{0}-l}{{l}_{0}}$$
(2)
$${\sigma }_{d}=\frac{F}{r{l}_{0}}$$
(3)
$${\epsilon}_{d}=\frac{{d}_{0}-d}{{d}_{0}}$$
(4)

where \(F\) is the force, \(r\) is the pellet radius, \({l}_{0}\) and \({d}_{0}\) are the initial pellet length and diameter, and \(l\) and \(d\) are the pellet length and diameter at the corresponding time, respectively. In addition, Young’s modulus \({(E}_{p})\) derived from the linear part of the stress–strain curve is reported.

3.2 Numerical method

The discrete element method (DEM) is proven as a powerful numerical method for modeling the granular material flow regimes [21,22,23,24], bulk material characterization [25, 26], breakage models [27,28,29,30,31], etc. In DEM, individual interactions of the particles are monitored contact by contact and the particle motion is modeled particle by particle [32]. Therefore, the properties of the particles are individually determined using the equations of motion, Eqs. (5) and (6), while the objective is to represent the macroscopic behavior of the bulk material.

$${m}_{i}\frac{{\rm {d}}{\upsilon }_{i}}{{\rm {d}}t}=\sum \left({F}_{ij}^{n}+{F}_{ij}^{t}\right)+{m}_{i}g$$
(5)
$${I}_{i}\frac{{\rm {d}}{\omega }_{i}}{{\rm {d}}t}=\sum \left({R}_{i}\times {F}_{ij}^{t}-{\tau }_{ij}^{r}\right)$$
(6)

where \({m}_{i}\), \({\upsilon }_{i}\), \({\omega }_{i}\), and \({I}_{i}\), are the mass, translational velocity, rotational velocity, and moment of inertia of particle \(i\), respectively. \(g\) is the gravity vector and \({F}_{ij}^{n}\) and \({F}_{ij}^{t}\) are the normal and tangential forces caused by the interaction between particles \(i\) and \(j\) at time-step \(t\). \({\tau }_{ij}^{r}\) is the torque between particles \(i\) and \(j\) and \({R}_{i}\) is the vector connecting the center of particle \(i\) to the location where \({F}_{ij}^{t}\) is applied as shown in Fig. 2.

Fig. 2
figure 2

Two particles interacting with each other in DEM

Full size image

The material breakage in DEM could be modeled using various models such as the particle replacement method (PRM), bonded particle method (BPM) [33], and fast-breakage model [34]. Recently, the so-called Timoshenko beam theory (also called Timoshenko–Ehrenfest beam theory [35]) model based on Timoshenko–Ehrenfest’s theory [36] was developed and validated by Brown [37] using EDEM® software provided by DEM Solutions Ltd., Edinburgh, Scotland, UK. The model is called the Edinburgh bonded particle model (EBPM) [37]. The main advantage of the EBPM model is the model capabilities of representing the normal, shear, bending, and torsion movements in a bond that has not been implemented in any other breakage model in DEM.

Plant-based biomass consists of lignocellulosic materials such as cellulose, hemicellulose, and lignin. In densification processes, lignin or supplementary binding agents act as a glue to bond the celluloses and hemicellulose particles. In order to numerically investigate the breakage behavior of densified biomass materials, a model containing particle bonding is required. In DEM, the lignocellulosic material could be represented by individual particles while the binding agents can be represented using bonds or beams.

3.2.1 Implementation of Timoshenko–Ehrenfest theory in DEM

The EBPM consists of two different contact models: Timoshenko–Ehrenfest beam theory and Hertz–Mindlin model. The former applies for bonded contacts and the latter applies for the non-bonded contacts. The model considers a cylindrical beam between the centers of every two neighboring particles at a user-defined time-step and bonds them in such a way that each bond breaks only if the applied force exceeds the maximum strength in compression, tension, or shear direction. Generally, each bond shares 6 degrees of freedom in each end, which allows compression, tension, and shear forces and torques as illustrated in Fig. 3. The domain of the neighboring particles is determined using a contact radius multiplier (CRM) which could be any number above 1. This number multiplies the particle radius and creates a virtual radius so that the model creates a bond between every two particles if their virtual radii overlap as shown in Fig. 4. Only one bond can exist between every two particles, and once a bond breaks it will never regenerate. The existence of the bonds is checked at each time-step, and once there is no bond anymore between every two neighboring particles the contact between them follows the Hertz–Mindlin model. The Hertz–Mindlin contact model is widely used in the literature due to its accurate calculations and computational efficiency [38, 39]. Detailed information about the Hertz–Mindlin contact model can be found elsewhere [39].

Fig. 3
figure 3

Schematic of a bond in the Timoshenko beam theory model. Each bond shares six degrees of freedom at each end

Full size image
Fig. 4
figure 4

Illustration of two spheres and their virtual radii in DEM

Full size image

The calculation of the force and momentum for bonded particles is based on the Timoshenko beam theory and is calculated at each time-step according to Eq. (7):

$$\left\{\varDelta F\right\}=\left[K\right].\{\varDelta u\}$$
(7)

where \(\varDelta F\) is the force vector and \(\varDelta u\) is the displacement vector and [K] is the stiffness matrix as shown in Eqs. (8) to (10):

$$ \begin{aligned} \{\varDelta F\} & =\left\{{\varDelta F}_{\alpha x }{\varDelta F}_{\alpha y }{\varDelta F}_{\alpha z }{\varDelta M}_{\alpha x }{\varDelta M}_{\alpha y }{\varDelta M}_{\alpha z} \right.\\ &\quad \left.{\varDelta F}_{\beta x }{\varDelta F}_{\beta y }{\varDelta F}_{\beta z }{\varDelta M}_{\beta x }{\varDelta M}_{\beta y }{\varDelta M}_{\beta z}\right\}^{T} \end{aligned} $$
(8)
$$ \begin{aligned} \left\{\varDelta u\right\} & =\left\{{\varDelta d}_{\alpha x }{\varDelta d}_{\alpha y }{\varDelta d}_{\alpha z }{\varDelta \theta }_{\alpha x }{\varDelta \theta }_{\alpha y }{\varDelta \theta }_{\alpha z}\right. \\ &\quad \left. {\varDelta d}_{\beta x }{\varDelta d}_{\beta y }{\varDelta d}_{\beta z } {\varDelta \theta }_{\beta x }{\varDelta \theta }_{\beta y }{\varDelta \theta }_{\beta z}\right\}^{T} \end{aligned} $$
(9)
$$ K = \left[ {\begin{array}{*{20}c} {K_{1} } &\quad { - K_{2} } &\quad { - K_{1} } &\quad { - K_{2} } \\ {K_{2} } &\quad {K_{3} } &\quad { - K_{2} } &\quad {K_{4} } \\ { - K_{1} } &\quad {K_{2} } &\quad {K_{1} } &\quad {K_{2} } \\ {K_{2} } &\quad {K_{4} } & \quad{ - K_{2} } &\quad {K_{3} } \\ \end{array} } \right] $$
(10)

where

$$\left[{K}_{1}\right]=\left[\begin{array}{ccc}\frac{E_{\rm {b}}A_{\rm {b}}}{L_{\rm {b}}}&\quad 0&\quad 0\\ 0&\quad \frac{12k}{L_{{\rm b}}^{2}(1+\Phi)}&\quad 0\\ 0&\quad 0&\quad \frac{12k}{L_{{\rm b}}^{2}(1+\Phi)}\end{array}\right]$$
(11)
$$\left[{K}_{2}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& \frac{-6k}{{L}_{\rm {b}}(1+\Phi)}\\ 0& \frac{6k}{{L}_{\rm {b}}(1+\Phi)}& 0\end{array}\right]$$
(12)
$$\left[{K}_{3}\right]=\left[\begin{array}{ccc}\frac{k}{(1+{v}_{\rm {b}})}& 0& 0\\ 0& \frac{k(4+\Phi)}{(1+\Phi)}& 0\\ 0& 0& \frac{k(4+\Phi)}{(1+\Phi)}\end{array}\right]$$
(13)
$$\left[{K}_{4}\right]=\left[\begin{array}{ccc}\frac{-k}{(1+{v}_{\rm {b}})}& 0& 0\\ 0& \frac{k(2-\Phi)}{(1+\Phi)}& 0\\ 0& 0& \frac{k(2-\Phi)}{(1+\Phi)}\end{array}\right]$$
(14)

where \({E}_{\rm {b}}\), \({v}_{\rm {b}}\), \({A}_{\rm {b}}\), \({L}_{\rm {b}}\), Φ, are the bond Young’s modulus, Poisson ratio, bond’s cross section area, bond length, and the Timoshenko bond coefficient, respectively, and k is calculated from Eq. (15).

$$k=\frac{{E}_{\rm {b}}{I}_{\rm {b}}}{{L}_{\rm {b}}}$$
(15)

where \({I}_{\rm {b}}\) is the second moment of area of the bond and is calculated from Eq. (16).

$${I}_{\rm {b}}=\frac{{r}_{\rm {b}}^{4}\pi }{4}$$
(16)

The radius of every bond is equal to the radius of the smaller sphere’s radius. Every bond is assigned a compressive (\({\sigma }_{C}\)), tensile (\({\sigma }_{{\rm T}}\)), and shear stress (\(\tau\)) limit which defines the maximum stress a bond can withstand before failure. The stress limits are calculated by Eqs. (17) to (19):

$${\sigma }_{C}={S}_{C}\cdot (\left({\varsigma }_{C}\cdot N\right)+1)$$
(17)
$${\sigma }_{\rm {T}}={S}_{{\rm T}}\cdot (\left({\varsigma }_{\rm {T}}\cdot N\right)+1)$$
(18)
$$\tau ={S}_{{\rm S}}\cdot (\left({\varsigma }_{{\rm S}}\cdot N\right)+1)$$
(19)

where \({S}_{C}\), \({S}_{{\rm T}}\), and \({S}_{{\rm S}}\) are the user-defined mean bond compressive, tensile, and shear strengths, respectively. \({\varsigma }_{C}\), \({\varsigma }_{{\rm T}}\), and \({\varsigma }_{{\rm S}}\) are the coefficient of variations of compressive, tensile, and shear strengths, respectively, which are defined by user and can be any number from zero to one. \(N\) is a random number derived from a normal distribution with a mean of zero and a standard deviation of one. Therefore, in a multi-sphere packing, depending on the value of the coefficient of variations of the bond strength (Eqs. (17)–(19)), a value between zero and twice the mean bond strength can be assigned for each bond stress limit.

3.2.2 Generation of pellet packing

Rigid spherical particles are considered in the model for simplicity, which means that the individual spherical particles do not crush or degrade. However, the bonds may break and separate the particles. The pellet configurations were created in GiD software [40] using multi-sphere particles. All the packing were created using the “Radius Expansion” algorithm with a delta radius factor of 0.2 and minimum and maximum radius factor of 0.7 and 1.3, respectively, with maximum 900 iterations. To investigate the effect of pellet packing resolution on the breakage behavior, different pellet configurations with a varying number of spheres and different radii were created using GiD software. The particle size distributions of the packing are shown in Fig. 5. All the created cylindrical pellets were 6 mm in diameter and 20 mm in length, while both ends were kept evenly smooth. Five different pellet configurations including 961, 2202, 3134, 5689, and 7965 spheres were created. There were three main assumptions for the selection of these configurations:

Fig. 5
figure 5

Cumulative mass-based distribution of the spheres used in different pellet packing

Full size image

  • Maximum sphere radius equal to 0.5 mm with various spheres radii in order to represent similar particle size distribution of biomass materials before the densification process.

  • Maximum 8000 spheres in a configuration due to limitations in the computational time.

  • No overlap between particles in order to allow particles to move freely when they face forces.

3.2.3 Calibration procedure

The aim of the numerical part was to simulate the compression tests of individual biomass pellets. Here, the model is calibrated only for the torrefied mixed wood pellets. The model was calibrated considering three key performance indicators (KPI) namely the stress at failure (\(\sigma\)), strain at failure (\(\epsilon\)), and Modulus of Elasticity (\({E}_{p}\)) for both uniaxial and diametrical compressions of torrefied mixed wood pellets. Due to heterogeneity in the real pellet structure [41], different stress–strain curves are obtained. In the calibration procedure, the mean of the stress, strain, and modulus of elasticity from the experimental results were taken into account. The first step was to screen the most influential parameters. For that, a series of simulations on different input parameters that are listed in Table 2 were carried out. The particle and bond Young’s modulus, the bond strength parameters, and CRM were found to be the most influential parameters. This is consistent with the other literature findings as the system is quasi-static [37]. Therefore, the particle–particle and particle–geometry parameters were found to be of less importance and the values used were chosen to represent a static condition.

Parker [42] characterized different properties of various types of wood species. According to him, Young’s modulus of wood lumbers is in the range of 5.5 to 11 GPa. Considering the densification process of wood pellets, which makes the materials stiffer than raw wood, Young’s modulus of 15 GPa for the spheres was considered in this study. There is no information about the maximum stress limits and the modulus of elasticity of the biomass bonds in the literature. However, the bond properties were calibrated to acquire the same stress–strain taking into consideration that most breakage mechanisms should be tensile [43].

3.2.4 Model inputs

The compression tests in the numerical method were executed using two parallel plates, which positioned on two sides of the pellet for each compression test as shown in Fig. 6. The compression rate of the plates was set to 10 mm s− 1 because lower compression rates were computationally impossible [44]. The model input parameters are shown in Table 2. Similar inputs are considered for the entire five pellet packing; however, as the particle radius distributions vary, the particle densities are selected differently as given in Table 3. In EDEM, material density is defined as the density of the particles. In order for simulated pellets to represent the real pellet mass, density for each configuration should be calculated based on the number of spheres and the porosity between them. Here, the goal of the numerical part was to model the breakage behavior of torrefied mixed wood. Therefore, the total mass of each pellet configuration with 6 mm diameter and 20 mm length and density of 1304 kg m− 3 should be 0.737 g.

Fig. 6
figure 6

Simulated pellets under uniaxial and diametrical compressions (yellow lines between the spheres show the bonds)

Full size image

It should be noted that the gravity was not considered in the simulations.

Table 2 Model input parameters
Full size table

The simulation time-step determines the minimum required time for a stable collision to happen. As the model contains two different contact models, i.e., the Timoshenko–Ehrenfest beam theory and the Hertz–Mindlin, the selected time-step should be the minimum required amongst the two contact models to ensure a stable simulation. The time-step for the Hertz–Mindlin contact model can be calculated as [44]:

$${\varDelta t}_{HM crit}=\frac{\pi { r}_{p}{\left(\frac{{\rho }_{p}}{{G}_{p}}\right)}^{0.5}}{(0.1631{\upsilon }_{p}+0.8766)}$$
(20)

where \({\rho }_{p}\) is the particle density, \({G}_{p}\) is the particle shear modulus, \({\upsilon }_{p}\) is the Poisson’s ratio, and \({ r}_{p}\) is the smallest particle radius. The shear modulus can be obtained from Eq. (21) using Young’s modulus and the Poisson’s ratio.

$${G}_{p}=\frac{{E}_{p}}{2(1+{\upsilon }_{p})}$$
(21)

For the bonded contact, the time-step is determined based on the smallest particle mass (\({m}_{p min}\)) and the largest bond stiffness component (\({K}_{b max}\)) [44].

$${{\Delta }t}_{b crit}=2\sqrt{\frac{{m}_{p min}}{{K}_{b max}}}$$
(22)

As shown in equations above, the minimum particle radius highly affects the minimum time-step. Consequently, the time-step for the simulations depends on the pellet configurations. The time-steps used in this study were between 0.045 and 0.75 µs.

As mentioned in Sect. 3.2.3, CRM was found as an important variable affecting the results of simulation because it directly affected the coordination number. The coordination number is defined as the total number of initial bonds over the total number of particles in the packing at time zero. In this study, two approaches were considered for the coordination numbers, a constant CRM and a constant coordination number for all the pellet configurations. For the first approach, a CRM of 1.2 was considered, and for the second approach, the CRM was adjusted to reach different coordination numbers between 3.49 and 4.72 for all the pellet configurations.

Table 3 Input parameters for different pellet packing
Full size table

3.2.5 Data analysis

The simulations have been continued until 20% drop in the forces on the compression plates after failure. Then, the stress–strain curves were drawn in the same manner as for the experiments. The force–displacements were achieved from the simulations as follows. The total force at every time-step was calculated as the mean value of the forces on the two plates. This is because of the minor deviations in the forces of the plates due to simulation errors. The displacement in axial and diametrical compressions was calculated based on the actual length or diameter of pellets at each time-step in comparison with the initial pellet length or diameter, respectively. To extract the exact pellet length or diameter at each time-step, the maximum overlap between the particles and plates were added to the distance of the plates. Then using Eqs. (1) to (4), the stress–strain data were calculated for uniaxial and diametrical compressions. The Young’s modulus of each pellet was then calculated from the linear part of the stress–strain curve.

4 Results and discussion

The results of the experimental compression tests, as well as the pellet densities are shown in Table 4, and a typical stress–strain curve for uniaxial and diametrical compressions of torrefied mixed wood pellets is depicted in Fig. 7, as an example. As the standard deviations show, there is a large variation between the experimental results of the maximum stress values even for one type of pellet in different test repetitions. It was also observed that for some pellets, for instance, TA265, the value of Young’s modulus differs significantly in axial and diametrical directions. Although it was not further studied in this work, it may be explained due to the heterogeneity in the pellet structure such as differences in porosity and the number and orientation of microcracks. Similar results were previously reported by other researchers [41]. Nevertheless, a deeper look at the pellets after compression tests shows that they mostly fail in shear as shown in Fig. 8.

Table 4 Experimental results and the standard deviations
Full size table
Fig. 7
figure 7

Typical experimental stress–strain curves for torrefied mixed wood pellets

Full size image
Fig. 8
figure 8

Pellets after experimental compression tests

Full size image

Table 5 shows the stress–strain simulation results at failure for different pellet configurations with CRM equal to 1.2. The stress–strain curves are depicted in Fig. 9 together with the experimental results. As it can be clearly seen, the results of the simulations are consistent with the experimental results where different pellet packing results in different values for the stress and strain at failure. The simulated pellet containing 5683 spheres shows the highest stress at failure for both uniaxial and diametrical compressions, while the pellet with 7965 spheres shows the lowest values for both compressions tests. The results reveal that there is a high linear correlation between the coordination numbers and the maximum stress at failure for all the simulated pellets. The results of the second approach where CRMs were adjusted to obtain uniform coordination numbers are shown in Fig. 10. The higher the coordination number, the higher the number of bonds in a system; thus, the higher the stress value at failure. Therefore, different material behavior can be reasonably reached by manipulating the coordination number. Detailed information on the strain–stress data for different coordination numbers are given in Online Resource 1.

Table 5 Simulation results of stress–strain at failure and Young’s modulus for different pellet configurations at CRM of 1.2
Full size table
Fig. 9
figure 9

stress–strain results for the uniaxial and diametrical compressions. Experimental versus simulations at CRM of 1.2

Full size image
Fig. 10
figure 10

Stress at failure versus coordination numbers for all the packing

Full size image

Figure 11 shows maximum stress at failure versus porosity for both axial and diametrical compressions. It is clearly seen that the stress at failure depends highly on porosity for axial compression; however, for diametrical compression, the correlation is less evident. Looking at Fig. 10, the pellet configuration made with 961 particles predicts the highest stress at failure in diametrical compression amongst all pellet packing. This is different from the results of axial compression where this packing is in the third order in terms of stress value at failure amongst all packing. This is clearer in Fig. 11 where 961 particles show the highest stress at failure. Figure 12 shows the stress at failure versus porosity for diametrical compression excluding the results of 961 particles. From Fig. 12, it is concluded that the stress at failure correlates highly with porosity for diametrical compressions as well. Therefore, the packing with 961 particle is an exception. The possible cause of this high stress value is probably the particle size in the packing. It was previously reported that there should be a sufficient number of particles along the width of a specimen to achieve a calibration [45]. In the packing with 961 particles, due to the bigger size of the particles in comparison with the other packing, there is a low number of particles in a row in the lengthwise direction, which affect the results of compression test.

Fig. 11
figure 11

Stress at failure versus porosity for all the packing

Full size image
Fig. 12
figure 12

Stress at failure versus porosity excluding the packing with 961 particles

Full size image

Comparing the experimental and numerical results in Fig. 9, the experimental results show more ductile behavior, progressive loading, and gradual collapse; however, the simulated pellets show more brittle behavior. In other words, in the experiments, the initial stress build-up is very small despite a relatively large displacement. There are at least two reasons for that. The first reason lies in the difference between the compression rates. As mentioned before, in this study the compression rate was 1 mm min− 1 in the experiments and 10 mm s− 1 in the simulations. At high compression rates, the materials show more rigid behavior [41], and therefore, the stress curve increases more straight than progressive. Second, this can be explained by the differences in the pellet structures. As real pellets mostly contain surface or internal cracks, the progressive loading is possibly due to the closures of the cracks at the start of compression [46].

Looking at literature in the field of rock cutting, Kemeny [43] claimed that although there is a complicated mechanism behind the crack growth under compression, it can be approximated by the crack with a central load point where the origins of the point loads are small regions of tension that develop in the same direction of the least principal stress. Considering his findings, the major bond breakage mechanism should be tension in a compression test. Figure 13 shows the total proportion of broken bonds at failure for every pellet configurations and share of each breakage mechanism at CRM of 1.2 and a coordination number of 4.19. As shown, the bond breakage due to tension is the major failure mechanism for all the pellet configurations. Similar results were observed for coordination numbers of 3.49 and 4.72. It should be noted that the total number of broken bonds may not be similar to the summation of the number of broken bonds due to compression, tension, and shear because in some cases a single bond may break due to multiple mechanisms at one time-step.

Fig. 13
figure 13

Fractions of the total broken bonds at failure and the bond failure due to tension, compression, and shear

Full size image

Online Resource 2 and Online Resource 3 show the breakage behavior of pellets after failure in simulations for CRM of 1.2. Comparing the breakage behavior in the experiments with those of the simulations, it is obvious that the breakage behavior is the same where pellets fail mainly due to shear albeit the main bond breakage failure mechanism is tension. This could be observed for all the simulated pellets except for the higher number of spheres, which increases the resolution and the notch formation. This is consistent with the previous research on bonded particle models [29]. The other difference between the uniaxial simulation results is the failure location in a pellet that is assumed to be related to the initiation of the microcracks inside pellets, which is probably a result of porosity distribution in a packing. This is a very complicated mechanism and requires further research. Nevertheless, for the diametrical compressions, the breakage happens at the top of the pellets for all the simulations. This is consistent with the experimental results, which are shown in Fig. 8.

It is worth mentioning that in this study, the amount and size of the particles released from the pellets during compression tests were not recorded, and therefore, that was not compared with the simulation results. As different pellet packing include different sphere’s radius distributions, some of the packing in this study may not represent the same particle size distribution of the released fines and dust. This requires more research to determine whether any of the used packing in this study could represent the breakage behavior of different pellet types. Nonetheless, for using the calibrated model in a bulk material, it is recommended to use a combination of these packing in order to represent the breakage behavior of different pellets.

Although the model was calibrated based on the experimental results of the torrefied mixed wood pellets, our study shows that the model could easily represent the breakage behavior of other types of pellets by changing the coordination numbers and/or by re-calibrating the values of the bond parameters.

5 Conclusions

Seven different types of biomass pellets were experimentally studied for the breakage behavior under uniaxial and diametrical compression tests. From the experimental results, it can be concluded that various pellet types show different stress–strain results due to different origins, pretreatment processes, and densification processes. The differences in results were also observed for pellets from the same type due to heterogeneity in the pellet structure. The heterogeneity might be due to the differences in the particle size distribution of the raw materials, heterogeneous porosity, existence of microcracks, etc. However, the maximum stress at failure for the tested pellets is in the range of 8.31 to 32.34 MPa.

The numerical results show that biomass pellets could be modeled using a multi-spherical approach where a different number of spheres can be applied to represent the mechanical strength of various types of biomass pellets. In our simulations, it was observed that the higher the coordination number and the lower the porosity, the higher the maximum stress at failure.

The breakage behavior of biomass pellets under uniaxial and diametrical compressions was successfully simulated for torrefied mixed wood pellets using discrete element methods. The model was based on the Timoshenko–Ehrenfest beam theory for bonded contacts and the Hertz–Mindlin theory for non-bonded contacts. The calibrated model is able to predict the stress–strain curves and the modulus of elasticity of the biomass pellets. This can pave the way for future numerical studies for biomass pellet production, transportation, and handling.