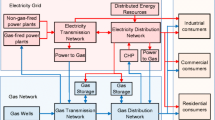
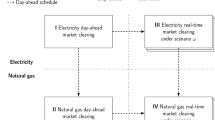
Abstract
The increasing interdependency of electricity and natural gas systems promotes coordination of the two systems for ensuring operational security and economics. This paper proposes a robust day-ahead scheduling model for the optimal coordinated operation of integrated energy systems while considering key uncertainties of the power system and natural gas system operation cost. Energy hub, with collocated gas-fired units, power-to-gas (PtG) facilities, and natural gas storages, is considered to store or convert one type of energy (i.e., electricity or natural gas) into the other form, which could analogously function as large-scale electrical energy storages. The column-and-constraint generation (C&CG) is adopted to solve the proposed integrated robust model, in which nonlinear natural gas network constraints are reformulated via a set of linear constraints. Numerical experiments signify the effectiveness of the proposed model for handling volatile electrical loads and renewable generations via the coordinated scheduling of electricity and natural gas systems.
Similar content being viewed by others
1 Introduction
The rapid growth of natural gas-fired units and the promising development of power-to-gas (PtG) technologies [1, 2] have intensified the interdependency of electricity and natural gas systems. Specifically, for power systems with a considerate amount of gas-fired units, electricity generation scheduling can be directly and significantly impacted by natural gas prices and/or gas production cost; energy reliability and security issues could be more severe when peak electrical loads occur coincidently with peak natural gas loads; and gas supplier outages, gas pipeline contingencies, and gas pressure losses could lead to the forced outage of multiple gas-fired units. On the other hand, natural gas system operators are facing with more volatile gas loads induced by gas-fired units, whose dispatches are often adjusted frequently to offset variations of electrical loads and renewable generations. As a result, it is imperative to consider and model the electricity grid and the natural gas network as an integrated energy system for achieving the coordinated optimal operation under uncertainties [3, 4].
The coordination of interdependent electricity and natural gas systems was studied in several literatures. Natural gas network constraints are incorporated in security-constrained unit commitment (SCUC) model for assessing the impact of natural gas network on power system operations [3, 5]. Reference [6] further considers transient characteristics of the natural gas infrastructure in the coordinated scheduling of electricity and natural gas systems. On the other hand, demand response is studied in the stochastic day-ahead scheduling of electricity and natural gas systems in [7], while hydro system is considered in the mid-term stochastic coordination to cover outages of gas units with insufficient gas supplies [8, 9]. In addition, in [10, 11], the natural gas production cost is added into the objective function to seek for optimal solutions of both systems with a novel mixed-integer linear programing (MILP) formulation.
The impact of variable renewable generation on the coordinated operation of interdependent electricity and natural gas systems is discussed in [12–14]. The influence of natural gas system on the short-term scheduling of power system with high penetration renewable energy is illustrated in [12]. Stochastic programming and robust optimization approaches are carried out in [13] and [14] respectively, to study coordinated scheduling of the two systems in the presence of volatile wind energy.
In fact, a high penetration of large wind farms has posed a number of challenges in power system operations. Specifically, as the penetration level of wind generation increases, wind spillage becomes more frequent with larger magnitudes. Indeed, due to the fact that large wind farms are exclusively located far away from load centers, significant investments in electrical transmission system have been required for effectively delivering wind power. On the contrary, PtG as an alternative energy storage technology has received increasing popularity for economically facilitating a high penetration of large wind farms [15, 16]. Unlike conventional electrical energy storage systems (e.g., pump-storage units and batteries) which consume and generate electrical energy at different time periods, PtG converts electricity into natural gas and uses natural gas network as a media to effectively transport/store electricity. The seasonal storage potential of PtGs is modeled in [17], and its effectiveness on power system and natural gas network operations is analyzed via the Great Britain gas and electrical transmission networks. Reference [18] investigates different PtG technologies and evaluates their impacts through a novel integrated model of electricity grid and gas transmission network. Reference [19] presents a multi-linear probabilistic energy flow framework while considering gas-fired generators, electric driven compressors, and PtG facilities. In [20], a robust co-optimization scheduling model considering the influence of PtG technology is proposed to coordinate the day-ahead operation of electricity and natural gas systems with uncertainties.
From existing literature we notice that: ① Robust optimization has been successfully used in power system operations for handling various uncertainties [21–24]. However, prior works on day-ahead robust coordinated operation of interdependent electricity and natural gas systems are rather limited; ② Most existing works do not fully address operation cost of the integrated energy system, such as operation cost of gas-fired units or production cost of the natural gas system; and ③ Gas-fired units and PtG facilities are treated as independent assets and optimized separately, while the coordination between gas-fired units, PtG facilities, and natural gas storages has not been investigated.
In order to address the challenges, this paper proposes an integrated robust optimization model to coordinate the operation scheduling of electricity and natural gas systems while considering electrical load and wind generation uncertainties. Instead of treading gas-fired units and PtGs as independent assets, the framework of energy hub is proposed to facilitate the effective coordination of the two. That is, the energy hub consists of gas-fired units to generate electricity when wind generation is low, PtG facilities to absorb excessive wind generation, and natural gas storages to store gas produced by PtG facilities and supply gas fuel to gas-fired units when needed.
The major contributions of this paper are twofold.
-
1)
The proposed integrated robust model coordinates the day-ahead scheduling of electricity and natural gas systems while considering power system uncertainties and natural gas system operation cost. Couplings between electricity and natural gas systems are rigorously formulated via the coordinated operation of gas-fired units and PtG facilities.
-
2)
Energy hubs with collocated gas-fired units, PtG facilities, and natural gas storages are considered, which could analogously function as large-scale electrical energy storages. The role of energy hubs to better accommodate electrical load and wind uncertainties is further explored for enhancing the economical and secure operation of integrated energy systems.
The rest of the paper is organized as follows. Section 2 presents the mathematical formulation of the proposed robust coordination scheduling model. Section 3 describes the solution methodology. Case studies on the 24-bus IEEE RTS system with a 12-node natural gas system are illustrated in Sect. 4, and the conclusions are drawn in Sect. 5.
2 Formulation of robust coordination scheduling
This section first presents an overview of gas-fired units and PtG facilities, which tightly tie the electricity grid and the natural gas network. The framework of an energy hub is further discussed. The robust coordinated scheduling formulation is presented according to similarities and differences of the two energy systems.
2.1 Overview
2.1.1 Gas-fired units
Gas-fired units consume natural gas to generate electricity, which leads to the growing reliance of the power system on the natural gas system in recent years. Accordingly, several concerns on the interdependency and reliability of both energy systems need be considered. ① Unlike coal and fuel oil, natural gas is usually not stored on-site. That is, gas-fired units rely on real-time delivery of natural gas fuel through the natural gas network. ② Residential gas loads have higher priorities than industrial gas-fired power plants. Thus, peak demands of natural gas end-users would significantly affect the delivery of interruptible gas transportation service to gas-fired power plants. ③ As an inspiring feature for offering flexible dispatch and fast ramping capabilities, gas-fired units are expected to play an important role in offsetting variability and uncertainty associated with renewable resources. In turn, the natural gas network needs to provide enhanced operational flexibility for meeting volatile gas demands of gas-fired units.
2.1.2 PtG technology
PtG as a new promising technology further intensifies the interdependency of electricity and natural gas systems, which could effectively convert excessive renewable energy into compatible natural gas. In addition, the existing natural gas infrastructure could potentially be used to store, transport, and reutilize this energy. In turn, the energy waste in terms of renewable generation curtailment can be prevented.
PtG consumes electricity to produce hydrogen or synthetic natural gas. PtG contains two main processes as shown in Fig. 1 [1]: ① electrolysis where electrical power is converted into hydrogen, and ② methanization where hydrogen along with carbon dioxide is further converted into methane. Typically, the efficiency of converting electricity to hydrogen and methane is about 54%–77% and 49%–65%, respectively [25]. In addition, in practice, there are technical and legislative restrictions on the quantity of hydrogen that may be blended into the natural gas network, whereas methane is compatible with natural gas. In this paper, the PtG process refers to the conversion of electricity to methane.
2.1.3 Energy hub
An energy hub represents the conversion and storage process of electricity and natural gas as shown in Fig. 2. In the figure, a gas-fired power plant, a gas storage device, and a PtG facility are located at the same geographic place. Furthermore, the gas-fired power plant and the PtG facility are connected at the same bus of the electricity grid, while all three equipment are connected to the same node of the natural gas network. From the perspective of power system operators, this energy hub (collocated gas-fired power plant and PtG facility) works analogous to a pump-storage asset while using the natural gas infrastructure as a gas reservoir. The energy hub enjoys the benefit that it could effectively mitigate variability of renewable generations. That is, the gas-fired unit can be scheduled to generate electricity when renewable generation is low, and to operate the PtG facility for converting excessive electricity into natural gas when renewable generation is high. Furthermore, as the energy hub can leverage the entire natural gas infrastructure as a gas reservoir, the maximum energy storage capability in the energy hub is not necessarily restricted by the collocated natural gas storage device. From the viewpoint of natural gas system operators, gas-fired units are considered as natural gas loads while PtG facilities are natural gas producers. Natural gas produced by PtG facilities could be either stored in the on-site gas storage or transported by natural gas network and consumed by other gas users. It is expected that when the PtG technology becomes more mature and economical, a deeper penetration of renewable generation can be facilitated.
2.2 Objective function
The robust day-ahead scheduling of integrated electricity and natural gas systems is to minimize the total costs associated with electric and natural gas energy supply and gas storage device operations in the base case. The objective function of the proposed integrated robust model is as follows:
where GU is set of gas-fired units; \(P_{it}^{b}\) is the base-case dispatch of unit i at time t; \(F_{i}^{c}\) and \(C_{i}^{\text{fuel}}\)are the heat rate curve and fuel price of unit i; \(SU_{it}^{b}\) and \(SD_{it}^{b}\) are startup and shutdown costs of unit i at time t; G jt is the gas production of natural gas supplier j at time t; \(Q_{st}^{\text{out}}\) is the natural gas outflow of storage facility s; \(C_{j}^{G}\) and \(C_{s}^{G}\) are the production and storage costs of natural gas supplier j and gas storage facility s, respectively.
2.3 Operation constraints
1) Energy production: In power systems, power outputs of individual units and power consumptions of individual PtG facilities are limited their by minimum and maximum capacities (2)–(3). Equation (4) indicates that generating units and PtG facilities connected at the same bus do not operate simultaneously. Generating units also need to satisfy minimum ON/OFF time limits (5)–(6), startup and shutdown cost constraints (7)–(8), ramp-up and ramp-down limits (9)–(10).
where \(I_{it}^{b}\) and \(I_{at}^{b}\) are commitment statuses of unit i and PtG facility a; \(P_{i}^{\hbox{min} }\) and \(P_{i}^{\hbox{max} }\) are minimum and maximum capacities of unit i; \(P_{at}^{b}\) and \(P_{a}^{\hbox{max} }\) are base-case dispatch and maximum capacity of PtG facility a; N(e) is set of components connected to bus e; \(X_{it}^{\text{on}}\) and \(X_{it}^{\text{off}}\) are ON and OFF time counters of unit i; \(T_{i}^{\text{on}}\) and \(T_{i}^{\text{off}}\) are minimum ON and OFF times of unit i; \(su_{i}\) and \(sd_{i}\) are startup and shutdown costs of unit i; \(UR_{i}\) and \(DR_{i}\) are ramp up and down rates of unit i.
For natural gas systems, production levels of gas suppliers are limited by their physical characteristics and/or contracted amount (11).
where \(G_{j}^{\hbox{min} }\) and \(G_{j}^{\hbox{max} }\) are minimum and maximum production levels of gas supplier j.
2) Energy storage: In power systems, as large-scale electric energy storage is still uneconomical, power supply and demand need to be balanced instantaneously. However, natural gas can be stored in large storage facilities for ensuring adequate supply of natural gas fuel. Thus, the flexibility provided by gas storage facilities can balance daily or seasonal gas demand variations. Indeed, gas storage facilities can be modeled similar as water reservoirs and batteries in power systems. Natural gas storage constraints include storage balance (12), storage capacity limit (13), as well as minimum and maximum injection and withdraw rates (14)–(15). Different from electrical energy storage devices in power systems which are associated with efficiency factors to account for electricity losses, the operation cost of gas storage devices is included in the objective function (1) to consider costs incurred by storing gas in and withdrawing gas out of gas storage devices.
where E st is the storage volume of gas storage facility s; \(Q_{st}^{\text{in}}\) and \(Q_{st}^{\text{out}}\) are natural gas inflow and outflow of storage facility s; \(E_{s}^{\hbox{min} }\) and \(E_{s}^{\hbox{max} }\) are minimum and maximum capacities of storage facility s; \(Q_{s}^{\hbox{min} }\) and \(Q_{s}^{\hbox{max} }\) are minimum and maximum flow rates of storage facility s.
3) Wind generation: The dispatch of wind power generation at each time period is limited by the hourly wind power availability (16). Since wind power does not incur operation cost and PtG facilities can convert excessive wind power into natural gas and consequently reduce the total gas production cost of natural gas system, wind energy will be economically utilized as much as possible.
where \(P_{wt}^{b}\) and \(P_{f,wt}^{b}\) are base-case dispatch and available wind generation of wind farm w at hour t.
2.4 Network constraints
1) Nodal balance: Both electricity and natural gas systems need to preserve the conservation of nodal balance of energy flows in the transmission network. Network nodal balances of the electricity grid (17) and the natural gas network (18) represent that the total energy injection is equal to the total withdrawn at each node.
where \(PL_{lt}^{b}\) is the base-case power flow of electric transmission line l; s(l)/s(mn) and r(l)/r(mn) are the sending bus/node and receiving bus/node of line l and pipeline mn; \(P_{dt}^{b}\) is base-case electricity demand of electrical load d; G(m) is set of gas network components connected at gas node m; GL mn,t is the natural gas flow of pipeline mn; G it and G at are gas consumption and production of gas-fired unit i and PtG facility a; G gt is gas demand of natural gas load g.
2) Energy flows: Electric transmission network is modeled via the DC power flow Eqs. (19)–(20) where power flow of a transmission line is determined by bus angles and the line impedance.
where \(\theta_{s(l)t}^{b}\) and \(\theta_{r(l)t}^{b}\) are the sending and receiving bus angles; x l is the reactance of line l; \(PL_{l}^{\hbox{max} }\) is the maximum power flow limit.
Similarly, gas flow in a pipeline can be expressed as a nonlinear function of nodal pressures and pipeline characteristics. The well-known Weymouth equations can be used to approximate gas flow equations under certain circumstances (21)–(22) [6].
where \(\pi_{mt}\) is the pressure square of gas node m; K mn is the Weymouth constant depending on pipeline characteristics.
It is worth mentioning that the steady-state natural gas flow model (21)–(22) would neglect built-in storage capabilities of pipelines (i.e., line pack) and slow travelling speeds of natural gas flows, as compared to the transient gas flow model [6]. Indeed, it is pointed out in [6] that the steady-state natural gas flow model might result in suboptimal schedules in the short-term coordinated operation of electricity and natural gas infrastructures.
3) Nodal constraints: Bus angles of the electricity grid and nodal pressures of the natural gas network are limited by their lower and upper bounds in (23) and (24), respectively. Note that lower and upper bus angle bounds of the reference bus are set to zero in (23).
where \(\theta_{e}^{\hbox{min} }\) and \(\theta_{e}^{\hbox{max} }\) are the minimum and maximum bus angle limits of electricity bus e; \(\pi_{m}^{\hbox{min} }\) and \(\pi_{m}^{\hbox{max} }\) are minimum and maximum nodal pressure square limits of gas node m.
Normally, natural gas flows of gas pipelines are driven by pressure difference of two adjacent nodes. With gas compressors installed in the natural gas network which are analogous to transformers in the power system, natural gas can flow from a low pressure node to a high pressure node. A simplified model of compressors from [26] is adopted in this paper (25).
where \(\varGamma_{c} > 1\) is the compressor factor, which facilitates natural gas flows from a low pressure node n to a high pressure node m.
2.5 Coupling constraints between electricity and natural gas systems
Gas-fired units represent the largest industrial natural gas consumer, and each gas-fired unit is considered as a natural gas load in the natural gas network. On the other hand, PtG facilities are regarded as natural gas producers in the natural gas system.
Natural gas consumption of gas-fired units and natural gas production of PtG facilities are determined by their hourly operation levels. In this paper, operation cost of gas-fired units is measured in terms of the natural gas production cost. The heat rate curve and high heating value (HHV) are used to model the relationship between gas consumption and electricity generation of gas-fired units (26). PtG facilities are modeled using energy conversion factor ϕ, efficiency \(\eta_{a}^{\text{PtG}}\), and HHV as in (27) [16, 27], where HHV = 1.026 MBtu/kcf and ϕ = 3.4 MBtu/ MWh.
2.6 Constraints for uncertainties
In this paper, the power system is designed to operate under the base case with unit commitment and generation dispatch decisions corresponding to forecasted values of electrical loads and wind generations in the day-ahead market, while generation dispatches can be adaptively and securely adjusted when possible realizations of uncertainties happen in real time. Only wind and electrical load uncertainties in power systems are considered in this paper. The reasons are twofold: 1) Electrical load uncertainty is a very important factor that will impact day-ahead power system operation schedules [21, 22, 24]. Thus, following the convention of traditional robust optimization based power system operation models, this paper considers electrical load uncertainty. 2) Natural gas system is regarded as highly reliable with sufficient line-pack capacities for handling gas load uncertainties [13], and in turn natural gas load uncertainty is usually not included. In addition, due to the nonlinearity of natural gas Weymouth flow equation, gas load uncertainty is very hard to be incorporated into the second-stage max–min robust framework. This mathematical challenge will be investigated in authors’ future work.
In order to ensure the operational security, the largest possible security violation ΔD under uncertainties should not exceed the preset security threshold ε RO (28). A bi-level max–min problem (29) is used to identify the largest possible security violation under uncertainties. Uncertainty sets of electrical loads and wind generations are described in (30)–(32). Adjusted dispatches need to satisfy nodal balance (33), power flow and bus angle constraint (34), power flow limit (35), bus angle limit (36), capacity limits (37)–(39), corrective ramp capabilities for coupling base-case dispatches and dispatch adjustments under uncertainty (40), as well as ramp up and down limits (41)–(42). In (33)–(43), \(P_{it}^{u}\), \(P_{at}^{u}\), and \(P_{wt}^{u}\) are adjusted dispatches of generating units, PtG facilities, and wind farms in response to uncertainty realizations of electrical load \(P_{dt}^{u}\) and wind generation \(P_{f,wt}^{u}\).
where v 1t and v 2t are slack variables; D and W are uncertainty sets of electrical loads and wind generations; NT, ND, and NW are numbers of hours, loads, and wind farms; \(z_{dt}^{ + }\), \(z_{dt}^{ - }\), \(z_{wt}^{ + }\), and \(z_{wt}^{ - }\) are binary indicators to describe uncertainty sets; Δ d and Δ w are uncertainty budgets which take values from 0 to NT; \(\tilde{P}_{dt}\) and \(\tilde{P}_{wt}\) are load and wind deviations; \(PL_{lt}^{u}\) and \(\theta_{et}^{u}\) are adjusted power flows and bus angles; λ are dual variables of corresponding constraints; \(R_{i}^{\text{down}}\)and \(R_{i}^{\text{up}}\) are corrective ramp up and down capabilities of units [21].
3 Solution methodology
The proposed robust coordination scheduling model is a large-scale, nonlinear, nondeterministic polynomial-time hard problem with uncertainty parameters. Benders Decomposition [21, 22] and Column-and- Constraint-Generation (C&CG) [23, 24] have been used to solve two-stage adjustable robust optimization problems. In this paper, the C&CG is employed to solve the proposed integrated robust scheduling model in a master-subproblem framework, by taking the advantage of its computational performance.
3.1 Master problem
The master UC problem minimizes the operation cost of the base case (1), subject to base-case constraints (2)–(27) and constraints (44)–(67) corresponding to worst case realizations of electrical load \(P_{dt,k}^{\text{worst}}\) and wind generation \(P_{f,wt,k}^{\text{worst}}\) identified in each iteration k of the subproblem.
In addition, as mixed-integer nonlinear programming problems are generally more difficult to solve, and power system operators exclusively use MILP models to solve day-ahead operation problems with stringent time requirements, this paper follows the convention to convert nonlinear natural gas flow Eqs. (21)–(22) into an MILP formulation with a better computational performance. That is, (21)–(22) are piecewisely linearized, which would convert the master UC problem into an MILP model. The detailed linear approximation of (21)–(22) are provided in “Appendix”. New solutions \(\hat{I}_{it}^{b}\), \(\hat{I}_{at}^{b}\), \(\hat{P}_{it}^{b}\), and \(\hat{P}_{at}^{b}\) are derived to securely handle all worst case realizations.
3.2 Worst case identification subproblem
Equations (29)–(43) is a bi-level max–min problem for identifying the largest possible security violation. It can be recasted into a single-level equivalent bilinear maximization problem by applying the duality theory on the inner linear programming (LP) problem. The resulting bilinear maximization problem is presented as follows:
The extreme point method is applied to further convert the bilinear maximization problem (68)–(77) into an MILP problem. Specifically, in the objective function (68), bi-linear terms represent products of primal and dual continuous variables, such as \(P_{dt}^{u} \cdot \lambda_{1,et}\). Such bilinear terms can be linearized by the extreme point method with auxiliary binary variables, because continuous uncertainty parameters always take either upper/lower limits or forecasted values [28] in the worst case. For instance, using the extreme point method, the bilinear term \(P_{dt}^{u} \lambda_{1,et}\) can be linearized as in (78)–(83).
where \(\lambda_{1,et}^{0}\), \(\lambda_{1,et}^{ + }\), and \(\lambda_{1,et}^{ - }\) are auxiliary continues variables corresponding to situations when \(P_{dt}^{u}\) takes the forecasted value, the upper bound, and the lower bound; \(\mu_{et}^{0}\), \(\mu_{et}^{ + }\), and \(\mu_{et}^{ - }\) are auxiliary binary variables corresponding to situations when \(P_{dt}^{u}\) takes the forecasted value, the upper bound, and the lower bound; M is a large enough positive number.
3.3 Implementation of the algorithm
The detailed solution procedure for implementing the C&CG algorithm is shown in Fig. 3. The major steps are described as follows.
-
Step 1: Set the maximum level of system power security violation under the worst-case scenario \(\varepsilon^{\text{RO}}\) and the iteration counter k = 1.
-
Step 2: Solve the master problem as described in Sect. 3.1, and pass the optimal solution \(\hat{I}_{it}^{b}\), \(\hat{I}_{at}^{b}\), \(\hat{P}_{it}^{b}\), and \(\hat{P}_{at}^{b}\) to the security checking subproblem (68)–(77).
-
Step 3: Solve the worst case identification subproblem (68)–(77) as described in Sect. 3.2 with respect to \(\hat{I}_{it}^{b}\), \(\hat{I}_{at}^{b}\), \(\hat{P}_{it}^{b}\), and \(\hat{P}_{at}^{b}\), and identify the worst case electrical load \(P_{dt,k}^{\text{worst}}\) and wind generation \(P_{f,wt,k}^{\text{worst}}\) which lead to the largest possible security violation.
-
Step 4: If the largest possible security violation is smaller than \(\varepsilon^{\text{RO}}\), terminate; Otherwise, generate C&CG constraints according to the worst case \(P_{dt,k}^{\text{worst}}\) and \(P_{f,wt,k}^{\text{worst}}\) in current iteration k, set k = k + 1, and go back to Step 2.
By iteratively solving the master problem, checking system security violations in the worst case identification subproblem, and consequently feeding identified worst cases back to the master problem, the C&CG algorithm can mathematically guarantee the global optimality of robust optimization problems [23]. Moreover, the worst case identification subproblem searches for worst case realizations within the uncertainty set that will lead to the largest possible security violations, while the number of identified worst cases is equal to the number of iterations of the C&CG algorithm. This number is system specific, which depends on factors like uncertainty budgets, load and wind profiles, and other system parameters.
4 Case studies
In this section, the 24-bus IEEE RTS system [29] with a 12-node natural gas system [30] is used to demonstrate the performance of the proposed approach. The 24-bus power system includes 26 generation units and 38 branches, with a peak electric demand of 2850 MW. 7 out of the 26 generation units in the 24-bus power system are gas-fired units. Generators 1–4 at buses 1, generator 5 at bus 16, and generators 6–7 at bus 23 are gas-fired units with capacity of 155 MW each, which are supplied by natural gas nodes 11, 5, and 12, respectively. The electric load profile in the winter weekday is chosen for the study. Capacities of all transmission lines are reduced to 60% of their original capacities [31]. Hydro units at bus 22 are replaced by a wind farm with the same capacity of 300 MW. In addition, another wind farm with the capacity of 200 MW is added at bus 18.
The 12-node natural gas system is shown in Fig. 4. The natural gas system includes 3 gas suppliers, 8 pipelines, 2 compressors, and 8 gas loads. Natural gas load demands at nodes 5, 11, and 12 are set as 500, 900, and 1600 kcf/h, respectively. One gas storage facility is added at node 5. Maximum inflow, maximum outflow, and maximum stored energy are 500, 500, and 4000 kcf, respectively. Other detailed system parameters are given in [30].
Fuel price for non-gas-fired units is 2.5$/MBtu. Production costs of the three gas suppliers are 2 $/kcf, 2 $/kcf, and 2.1 $/kcf, respectively. Operation cost of the gas storage is 0.3 $/kcf, to account for costs incurred by storing gas in and withdrawing gas out of gas storage devices. Two PtG facilities are included in the integrated energy system. The two PtG facilities are connected at buses 16 and 17 of the power grid, and at nodes 5 and 3 of the natural gas network. Capacities of PtG1 and PtG2 are 100 and 50 MW respectively with efficiency of 0.64. Note that gas-fired unit and PtG facility at electricity bus 16 and gas node 5 along with the gas storage form an energy hub in the integrated energy systems.
The following five cases are studied for illustrating the proposed robust coordination approach of electricity and natural gas systems. All case studies are implemented in MATLAB and solved using Gurobi 6.5 on a personal laptop with Intel Core i7 2.6 GHz processor and 12 GB memory.
-
Case 1: Deterministic case without PtGs.
-
Case 2: Case 1 with PtGs.
-
Case 3: Robust coordination is considered in Case 1.
-
Case 4: Robust coordination is considered in Case 2.
-
Case 5: Case 4 with different uncertainty budget levels.
Case 1: Power system uncertainties and PtG technology are not considered in this case. In this case, wind generation peaks occur during hours 3–6 where electrical loads are at off-peak. Due to ramping capacity limits and minimum down time constraints of generating units as well as transmission congestions, available wind energy cannot be fully utilized. As a result, a total amount of 89.72 MWh of wind generation is spilled during these 4 h in the early morning. The total operation cost of electricity and natural gas systems is shown in Table 1. In the deterministic day-ahead coordination scheduling, a total number of 477 units are committed during the 24-h horizon as shown in Table 1.
Case 2: PtG is considered in this case for economically converting excessive wind energy to compatible natural gas, which is otherwise spilled in Case 1. Natural gas produced by PtG facilities is transported and consumed by other natural gas loads. Since this amount of natural gas is produced by excessive wind energy which is otherwise spilled, the total system operation cost is reduced to $1220094.8 as shown in Table 1.
Case 3: Variations of electrical loads and wind generations are taken into account in this case by the robust coordination strategy. Uncertainty intervals of electrical loads and wind generations are considered as 10% and 20% of their forecast values, respectively, i.e. \(\tilde{P}_{dt} = 0.1 \cdot P_{dt}^{b}\) and \(\tilde{P}_{wt} = 0.2 \cdot P_{f,wt}^{b}\) in (30)–(31). Uncertainty budgets \(\Delta_{d}\) and \(\Delta_{w}\) are both set as 24. The security violation threshold \(\varepsilon^{\text{RO}}\) in (28) is set to 0.01 MW, which means that the system will be immune against all possible realizations of electrical loads and wind generations within the predefined uncertainty set.
The forecasted value, lower bound, upper bound, and identified worst case of electrical loads and wind generations are shown in Figs. 5 and 6, respectively. It can be seen that at hours 5–6, electrical load is low and wind generation is high, whereas electrical load is high and wind generation is low during load peak hours 16–20. In addition, the situation becomes even worse in the worst case situations. The day-ahead robust security-constrained unit commitment (SCUC) is designed to handle worst case situations while avoiding electrical load shedding. Compared with Case 1, 484 units are committed which indicates that more ramping capabilities are needed to handle uncertainties of electrical loads and wind generations. As a result, the total operation cost is increased to $1223397.5.
Case 4: PtG facility in the energy hub is considered based on Case 3. In this case, PtG can provide ramping down capabilities for power systems by converting excessive wind energy into natural gas. With more ramping capabilities, other units can operate at more economical states. In addition, natural gas produced by PtG can reduce the gas production cost for supplying natural gas loads. In turn, the total operation cost is decreased to $1222210.4 as compared to Case 3.
In Case 4, the energy hub plays an important role in the conversion and storage of energy, in order to ensure economic and secure operation of interdependent systems. The collocated gas-fired unit and PtG facility behave like a pump-storage unit while using the natural gas infrastructure as reservoir, which can help reduce variations of electrical loads and wind generations. The combined net power outputs of gas-fired unit and PtG facility under the base case and the worst case are further shown in Fig. 7, where positive and negative values represent power generation of gas-fired unit and power consumption of PtG facility, respectively. Inflows and outflows of the gas storage facility are further shown in Fig. 8 as positive and negative values.
As shown in Fig. 7, the PtG facility is operated in hours 1–6 while the gas-fired unit works for the rest of the day. It is observed in Figs. 5 and 6 that wind generation is relatively high in hours 1–6 where the system cannot provide enough down ramping capabilities to effectively utilizing available wind energy. In turn, PtG is called to help converting excessive wind energy into natural gas, which will prevent wind spillage and facilitate an economic operation. For the remaining hours where electrical load is relatively high, the gas-fired unit is operated to generate electricity and maintain power system security by providing up/down ramping capabilities to handle worst cases. It should be noted that power outputs of gas-fired unit and power consumptions of PtG facilities increase in worst cases.
Figure 8 further shows that natural gas storage facility is used more frequently under the worst case, in response to frequent hourly dispatch changes of gas-fired unit and PtG facility as shown in Fig. 7. Because operating natural gas storage facility incurs costs, it is rarely used in the base case unless operational economics can be improved. Specifically, in hours 5–6 of the base case when wind generation is high, natural gas produced by the PtG facility cannot be transported to gas loads due to natural gas network congestion caused by gas nodal pressure limits, and in turn a certain amount of natural gas is stored on site in the storage facility and used later at hour 7. On the other hand, in the worst case, more natural gas is injected into and withdrawn out of the storage facility to provide enough gas fuel for supporting ramping and generating capabilities of the gas-fired unit when electrical load is high. In addition, in hours 21–23, natural gas is injected into gas storage facilities to secure gas fuel supply to gas-fired units in the next operation day.
Case 5: In this case, the impact of different uncertainty budget levels on the total cost and worst-case load shedding of the integrated energy system is studied. Worst-case load shedding cost is set as $1000/MWh. The results are reported in Table 2. Specifically, when the uncertainty budget is 0, the integrated robust model degrades to the deterministic model because no uncertainty is considered. As uncertainty budget increases, results are more conservative and the system is immune to a higher level of uncertainties since a larger total deviation of load and wind generation is considered. In turn, the total cost increases monotonously as a wider range of uncertainties is covered. On the other hand, worst-case operation cost decreases because load shedding in the worst case is reduced. When uncertainty budget reaches 16, the total cost does not increase any further and worst-case operation cost does not change any more, which indicates that enough generators have been committed online and adequate system flexibilities are readily available for handling uncertainties. In addition, load shedding quantity is smaller than the security threshold \(\varepsilon^{\text{RO}}\) of 0.01 MW under any possible load and wind generation realizations within the uncertainty set, which justifies that the proposed robust model can derive secure operation solutions for the integrated energy system with uncertainties.
As robust optimization and stochastic programming have been recognized as two effective approaches for handling uncertainties in optimization problems, solutions of the proposed robust model and the stochastic programming model [31, 32] are further compared. In the stochastic programming model, electrical load and wind power uncertainties are assumed to follow uniform distributions. 5000 scenarios are generated via the Latin hypercube sampling method for simulating uncertainties of electrical loads and wind generations in a 24-h period. Then the number of reduced scenarios is chosen to be 10 as a trade-off between computational speed and solution quality [32]. The worst-case load shedding and the operation cost of the stochastic programming model are reported in Table 2. It is observed in Table 2 that the stochastic programming model derives results closer to that of the proposed robust model with uncertainty budget of 1. Specifically, results obtained by the stochastic programming model could yield a smaller cost for covering high-probability scenarios, while the system may not be robust because it could lead to relatively high system load shedding when low-probability high-impact worst case occurs.
Computational performance of the proposed robust model and the stochastic model is further compared in Table 3. The proposed robust model with uncertainty budget of 1 has identified 12 worst cases and yields a total computational time of 4441 s. This high computational time is mainly caused by 12 C&CG iterations and the complexity of worst-case natural gas constraints. In comparison, the stochastic model with 10 scenarios achieves a shorter computational time of 709 s, partly because the worst-case identification subproblem is not involved. In addition, uncertainty budget would also impact computational performance of the proposed robust model. Indeed, total computational time of the proposed robust model with uncertainty budget of 24 is reduced to 142 s, because the identified worst-case scenario is reduced to 1 and the number of C&CG iterations has been greatly reduced.
5 Conclusion
This paper proposes an integrated robust model to coordinate the day-ahead scheduling of electricity and natural gas systems. The energy hub with collocated gas-fired unit, PtG facility, and natural gas storage is explored. The integrated robust model is solved by C&CG algorithm under a master-subproblem framework. Nonlinear natural gas constraints are piecewisely linearized and added into the master problem for the optimal solution. The bi-level subproblem which identifies the worst case situations is recasted into a single-level bilinear problem and then further reformulated an MILP problem via the extreme point method.
Simulation results indicate that PtG facilities can positively contribute to wind spillage mitigation by effectively converting excessive wind generation into natural gas. The robust optimization technique ensures the security of the interdependent energy system with volatile electrical loads and wind generations by committing more units to provide enough ramping capabilities. Furthermore, energy hubs with collocated gas-fired units, PtG facilities, and natural gas storages can be operated analogously as a pump-storage device, which further enhance system flexibilities. Indeed, the energy hub could help achieve an economical and secure operation scheduling by firming the variability of wind generations and electrical loads. In turn, the proposed integrated robust model would enable system operators to securely and economically schedule the interdependent energy system under different levels of uncertainties.
References
Götz M, Lefebvre J, Mörs F et al (2016) Renewable power-to-gas: a technological and economic review. Renew Energy 85:1371–1390
Gahleitner G (2013) Hydrogen from renewable electricity: an international review of power-to-gas plants for stationary applications. Int J Hydrog Energy 38(5):2039–2061
Li T, Eremia M, Shahidehpour M (2008) Interdependency of natural gas network and power system security. IEEE Trans Power Syst 23(4):1817–1824
Wei Z, Chen S, Sun G et al (2016) Probabilistic available transfer capability calculation considering static security constraints and uncertainties of electricity-gas integrated energy systems. Appl Energy 167:305–316
Liu C, Shahidehpour M, Fu Y et al (2009) Security-constrained unit commitment with natural gas transmission constraints. IEEE Trans Power Syst 24(3):1523–1536
Liu C, Shahidehpour M, Wang J (2011) Coordinated scheduling of electricity and natural gas infrastructures with a transient model for natural gas flow. Chaos J 21(2):1–12
Zhang X, Shahidehpour M, Alabdulwahab A et al (2016) Hourly electricity demand response in the stochastic day-ahead scheduling of coordinated electricity and natural gas networks. IEEE Trans Power Syst 31(1):592–601
Wu L, Shahidehpour M (2011) Optimal coordination of stochastic hydro and natural gas supplies in midterm operation of power systems. IET Gener Transm Distrib 5(5):577–587
Kamalinia S, Wu L, Shahidehpour M (2014) Stochastic midterm coordination of hydro and natural gas flexibilities for wind energy integration. IEEE Trans Sustain Energy 5(4):1070–1079
Correa-Posada C, Sanchez-Martin P (2014) Security-constrained optimal power and natural-gas flow. IEEE Trans Power Syst 29(4):1780–1787
Correa-Posada C, Sanchez-Martin P (2015) Integrated power and natural gas model for energy adequacy in short-term operation. IEEE Trans Power Syst 30(6):3347–3355
Zhang X, Che L, Shahidehpour M (2015) Impact of natural gas system on short-term scheduling with volatile renewable energy. IEEE power and energy society general meeting, Denver, CO, USA, 1–5, 5pp
Alabdulwahab A, Abusorrah A, Zhang X et al (2015) Coordination of interdependent natural gas and electricity infrastructures for firming the variability of wind energy in stochastic day-ahead scheduling. IEEE Trans Sustain Energy 6(2):606–615
Liu C, Lee C, Shahidehpour M (2015) Look ahead robust scheduling of wind-thermal system with considering natural gas congestion. IEEE Trans Power Syst 30(1):544–545
Walker SB, Mukherjee U, Fowler M et al (2016) Benchmarking and selection of power-to-gas utilizing electrolytic hydrogen as an energy storage alternative. Int J Hydrog Energy 41(19):7717–7731
Qadrdan M, Abeysekera M, Chaudry M et al (2015) Role of power-to-gas in an integrated gas and electricity system in Great Britain. Int J Hydrog Energy 40(17):5763–5775
Clegg S, Mancarella P (2016) Storing renewables in the gas network: modelling of power-to-gas seasonal storage flexibility in low-carbon power systems. IET Gener Transm Distrib 10(3):566–575
Clegg S, Mancarella P (2015) Integrated modeling and assessment of the operational impact of power-to-gas (P2G) on electrical and gas transmission networks. IEEE Trans Sustain Energy 6(4):1234–1244
Chen S, Wei Z, Sun G et al (2016) Multi-linear probabilistic energy flow analysis of integrated electrical and natural-gas systems. IEEE Trans Power Syst. doi:10.1109/TPWRS.2016.2597162
He C, Wu L, Liu T et al (2017) Robust co-optimization scheduling of electricity and natural gas systems via ADMM. IEEE Trans Sustain Energy 8(2):658–670
Hu B, Wu L, Marwali M (2014) On the robust solution to SCUC with load and wind uncertainty correlations. IEEE Trans Power Syst 29(6):2952–2964
Dai C, Wu L, Wu H (2016) A multi-band uncertainty set based robust SCUC with spatial and temporal budget constraints. IEEE Trans Power Syst 31(6):4988–5000
Zeng B, Zhao L (2013) Solving two-stage robust optimization problems using a column-and-constraint generation method. Operations Research Lett 41(5):457–461
Ye H, Li Z (2015) Robust security-constrained unit commitment and dispatch with recourse cost requirement. IEEE Trans Power Syst 31(5):3527–3536
Jentsch M, Trost T, Sterner M (2014) Optimal use of power-to-gas energy storage systems in an 85% renewable energy scenario. Energy Procedia 46:254–261
Tomasgard A, Rømo F, Fodstad M et al (2007) Optimization models for the natural gas value chain. In: Geometric modelling numerical Simulation and optimization. Springer, New York, pp 521–558. doi:10.1007/978-3-540-68783-2_16
Energy star (2015), Portfolio manager technical reference: thermal conversion factors. https://www.energystar.gov/buildings/tools-and-resources/portfolio-manager-technical-reference-thermal-conversion-factors. Accessed 25 Oct 2016
White DJ (1992) A linear programming approach to solving bilinear programmes. Math Progr 56(1–3):45–50
Reliability Test System Task Force (1999) The IEEE reliability test system-1996. IEEE Trans Power Syst 14(3):1010–1020
Pantos M (2011) Market-based congestion management in electric power systems with increased share of natural gas dependant power plants. Energy 36(2):4244–4255
Wu L, Shahidehpour M, Li T (2007) Stochastic security-constrained unit commitment. IEEE Trans Power Syst 22(2):800–811
Wang J, Shahidehpour M, Li Z (2008) Security-constrained unit commitment with volatile wind power generation. IEEE Trans Power Syst 23(3):1319–1327
McCormick GP (1976) Computability of global solutions to factorable nonconvex programs: part I-convex underestimating problems. Math Program 10(1):147–175
Geißler B, Martin A, Morsi A et al (2012) Using piecewise linear functions for solving MINLPs mixed integer nonlinear programming. Springer, New York, pp 287–314
Correa-Posada C, Sanchez-Martin P (2014) Gas network optimization: a comparison of piecewise linear models. http://www.optimization-online.org/DB_FILE/2014/10/4580.pdf
Acknowledgements
This work was supported in part by the U.S. National Science Foundation Grant (No. CMMI-1635339).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 8 March 2017
Appendix A
Appendix A
Equations (21)–(22) is presented as a group of nonlinear equations. Here an auxiliary binary variable f is introduced to reformulate (21)–(22) as (A1)–(A4).
where \(f_{mn,t}^{ + }\) and \(f_{mn,t}^{ - }\) are the gas flow direction of pipeline mn, i.e., \(f_{mn,t}^{ + } = 1\) means natural gas flows from node m to node n.
The auxiliary variable r is further introduced in (A5) to represent the bilinear products. Well-known algebra results in [33] are used to equivalently recast (A5)–(A6).
where \(\pi_{mt}^{l}\) and \(\pi_{mt}^{u}\) are the lower and upper limits of pressure square of node m at time t.
Furthermore, the univariate squared function \(y = x^{2}\) of gas flow square defined within an interval can be piecewisely approximated [34, 35] as in (A7)–(A9), which is further shown in Fig. 9. Continuous variable x is divided into h segmental values \(\delta_{l}\) starting from \(\bar{x}_{0}\), as described in (A7). The linearized function value is calculated via (A8). Binary variable \(z_{l}\) is used to force the so-called “filling condition” (A9)–(A10), i.e. \(\delta_{l} > 0\) implies that \(\delta_{l - 1}\) is at its upper bound.
Reference [35] compared three different models to linearize nonlinear gas flow constraints, including convex combination model, multiple choice model, and incremental model. Theoretical and computational analysis in [35] indicates that the incremental model outperforms the other two techniques. Indeed, the most promising advantage of incremental model is its computational performance for optimizing gas network operations. Thus, the incremental model is adopted in this paper. Regarding squared nodal gas pressure, the operating interval is usually given according to technique limitations, security reasons, or contracted quantities. Once the intervals of nodal gas pressure are defined, intervals of gas flows can be calculated via Eq. (21). Normally, operating intervals of gas flows can be tuned according to real operation conditions for further improving computational performance and solution quality.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
HE, C., LIU, T., WU, L. et al. Robust coordination of interdependent electricity and natural gas systems in day-ahead scheduling for facilitating volatile renewable generations via power-to-gas technology. J. Mod. Power Syst. Clean Energy 5, 375–388 (2017). https://doi.org/10.1007/s40565-017-0278-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0278-z