1 Introduction

Along with the rising concern about serious energy crisis and environmental pollution, the wind power generation technologies have gained comprehensive attention in recent decades. With regard to the performance test of control strategies for wind energy conversion systems (WECS), the experiments on field wind turbines (WT) are costly and unrepeatable. Therefore, wind turbine simulators (WTS) have become necessary and convenient tools for preliminary experiments.

A WECS mainly consists of the electric system and aero-mechanical system, which are usually dissociated and studied separately [1–3]. Correspondingly, there are also two types of WTS systems built in the current literatures. On the one hand, the grid-connection and the electric power quality are focused [4–8]. On the other hand, Reference [9–21] concern the aero-mechanical dynamics to provide a performance test rig for WT control strategies. This paper will focus on the latter type.

Because the slow dynamics of WTs resulted from high rotor inertia is one of key issues in the control strategy design of WTs [1, 2, 22, 23], the WTS should replicate the mechanical behavior similar to field WTs [9–20]. However, the moment of inertia of WTSs is usually much smaller than that of WTs, and therefore the inertia compensation scheme is applied to simulate the slow behavior of mechanical dynamics of WTs [10–19].

However, it has been found that when simulating a WT with large rotor inertia, the WTS applying the inertia compensation scheme might be unstable and the instability is characterized by the asymptotic divergence of compensation torque [10–12]. It is intuitively pointed out that the external noise of speed measurement in the differential-based acceleration observation used by the inertia compensation scheme is responsible for this instability, and accordingly a low-pass filter (LPF) is recommended to attenuate the interference signal [11, 12]. The similar implementation of LPF for the external noise elimination is also presented [4, 16]. Moreover, in order to avoid the differential-based acceleration observation that can easily exaggerate the external noise of speed measurement, the pseudo derivative feedback [13] and estimation of the load torque [14] are proposed which, however, increase the complexity of WTS implementation.

Different from the aforementioned literatures which focus on improving the acceleration observation by removing differentiator, in this paper such type of instability of WTS is investigated and its cause is perceived as the one-step time delay of the differential-based acceleration observation rather than the external noise of speed measurement. Furthermore, by depicting the deviation of response between WTS and WT, a deviation mitigation method, which can be easily realized by a first-order filter added in the inertia compensation scheme, is proposed and the criterion for selecting the filter coefficients is provided. Note that this filter aims to mitigate the divergent deviation response stimulated by the time delay in acceleration observation. When employing the proposed inertia compensation scheme based on deviation mitigation, the slow dynamic behavior of WTs can be replicated stably and conveniently. Finally, both simulations and experiments are conducted to verify the proposed inertia compensation scheme.

2 Modeling of the WTS

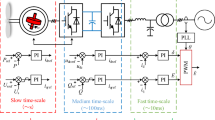
As illustrated in Fig. 1, the WTS system mainly consists of two subsystems, a real-time digital control system (DCS) and a torque-controlled motor as the replaced prime mover [7–21]. With the simulation algorithm running in DCS, torque-controlled motor can mimic the aerodynamic and mechanical behavior of WTs.

Fig. 1
figure 1

Structure of the WTS-based wind energy conversion system

Full size image

2.1 Aerodynamic model of WT

The aerodynamic torque of WT driven by inflow wind can be expressed by:

$$T_{a} = 0.5\rho \pi R^{2} v^{3} C_{p} (\lambda ,\beta )/\omega_{t}$$
(1)

where ρ is the air density (kg/m3); R is the radius of the wind turbine (m); v is the wind speed (m/s); ω t is the rotor speed (rad/s); C p is the power coefficient which is a nonlinear function of the tip speed ratio (TSR) and the blade pitch angle β, as shown in Fig. 2. TSR \(\lambda\) is expressed as:

$$\lambda = \omega_{t} R/v$$
(2)
Fig. 2
figure 2

C p curve as a function of TSR λ and the blade pitch angle β

Full size image

2.2 Mechanical dynamics of WT and WTS

Assuming that the main shaft and the gearbox are infinitely rigid, the drive train of WT can be regarded as a one-mass model [22]:

$$T_{a} /n_{g} - T_{g} = J_{t} \dot{\omega }_{g}$$
(3)

where J t is the moment of inertia on high-speed shaft side of drive chain (kgm2); n g is the transmission ratio of gearbox; ω g and T g are the generator speed (rad/s) and generator torque (Nm), respectively.

Likewise, the mechanical dynamics of WTS can be expressed as:

$$T_{s} - T_{g} = J_{s} \dot{\omega }_{s}$$
(4)

where T s is the motor torque produced from the prime mover (Nm); J s is the total moment of inertia of WTS (kgm2); ω s is the rotational shaft speed of WTS (rad/s).

By comparing (3) and (4), it is obvious that because the inertia of WTS \(J_{s}\) is much smaller than that of WT \(J_{t}\), WTS cannot replicate the mechanical dynamics similar to WT even if the motor torque \(T_{s}\) is controlled following the aerodynamic torque \(T_{a} /n_{g}\).

To obtain the similar mechanical dynamics, the inertia compensation scheme is employed by WTS [10–19]. By subtracting (3) from (4) based on the assumption that \(\dot{\omega }_{s}\) is equal to \(\dot{\omega }_{g}\), the rearrangement gives:

$$T_{s} = T_{a} /n_{g} - (J_{t} - J_{s} )\dot{\omega }_{g}$$
(5)

where \((J_{t} - J_{s} )\dot{\omega }_{g}\) represents the dynamic compensation torque T comp which is calculated according to the acceleration of rotational shaft. Thus, the mechanical dynamics of the two systems would be identical if the motor torque is compensated by T comp . Besides, since a differentiator for acceleration observation is adopted in the torque compensation loop, the external noise \(\zeta\) of speed measurement should be considered [11, 12] and the conventional model of WTS is then depicted in Fig. 3.

Fig. 3
figure 3

Block diagram of the WTS with inertia compensation scheme

Full size image

2.3 Discrete model of torque compensation loop

The differential equations implemented in DCS need to be discretized. The rotational acceleration is commonly obtained by the difference calculation of successive measured speeds. Therefore, the observed acceleration \(\alpha_{comp}\) in the torque compensation loop (marked in Fig. 3) is calculated by:

$$\alpha_{comp} (k) = [\omega_{g} (k) - \omega_{g} (k - 1)]/T$$
(6)

where T is the sampling interval of rotational speed which depends on the fixed-time step of DCS. Likewise, the integral element is discretized as follows:

$$\omega_{g} (k + 1) = \omega_{g} (k) + \alpha (k) \cdot T$$
(7)

where \(\alpha (k)\) is the average acceleration between two successive sampling points, i.e., kT and (k + 1)T. Substituting (7) into (6), it is obtained that

$$\alpha_{comp} (k) = \alpha (k - 1)$$
(8)

This indicates that the one-step time delay, which is irrelevant to the real-time sampling period, is inevitably induced in the discretization process of torque compensation loop. Then, regardless of the nonlinear aerodynamics, the mechanical dynamics of WTS including the one-step time delay and external noise are modeled in Fig. 4a. Similarly, the mechanical dynamics of WT is discretized and illustrated in Fig. 4b. Note that the external noise is not included in the discrete model of WT.

Fig. 4
figure 4

Discrete models of mechanical dynamics of WTS and WT

Full size image

3 Analysis on the instability of WTS

In this section, in order to simplify the stability analysis of WTS, the generator torque is approximated as a linear function of rotational speed, i.e.

$$T_{g} = k_{L} \cdot \omega_{g}$$
(9)

where \(k_{L}\) is the linearized load factor. Then, the linear time-invariant models of WTS and WT are obtained.

3.1 Stability analysis on the WT model

Regarding the driving torque \(T_{a} /n_{g}\) as the input and \(\omega_{g}\) as the output, the transfer function of the WT model is derived as follows:

$$H_{real} (z) = \frac{{T/J_{t} }}{{z + T \cdot k_{L} /J_{t} - 1}}$$
(10)

If the WT is stable, the root of the characteristic equation of (10) should be located in the unit circle. Therefore, the stability condition of WT is obtained as:

$$0 < T \cdot k_{L} < 2J_{t}$$
(11)

This condition is always satisfied because the magnitude of \(T \cdot k_{L}\) is much smaller than that of \(J_{t}\).

3.2 Stability analysis on the WTS model with external noise

Then, this section analyzes the stability of the WTS model in which, as illustrated in Fig. 5, the external noise is considered and the one-step time delay of acceleration observation is neglected by adding a z element in the torque compensation loop. Correspondingly, the observed acceleration \(\alpha_{comp}\) exactly synchronizes with the real acceleration \(\alpha\) without influencing the generator torque \(T_{g}\) and the noise \(\zeta\).

Fig. 5
figure 5

Discrete model of WTS with the one-step time delay neglected

Full size image

Letting \(T_{a} /n_{g}\) be zero input, taking the external noise ζ as the input and the compensation torque \(T_{comp}\) as the output, the transfer function of the WTS model shown in Fig. 5 is derived as:

$$H_{wts}^{noise} = \frac{{\left( {1 - z^{ - 1} } \right)\left( {J_{t} - J_{s} } \right)\left[ {(z - 1)/T + k_{L} /J_{s} } \right]/J_{t} }}{{z + T \cdot k_{L} /J_{t} - 1}}$$
(12)

It can be seen that the characteristic equation of (12) is the same with that of the WT model in (10). This indicates that, so long as the configurations of WT (i.e., \(T\), \(J_{t}\) and \(k_{L}\)) satisfy the stability condition (11), the WTS without the one-step time delay in the acceleration observation is stable even if it is disturbed by the external noise.

3.3 Stability analysis on the WTS model considering the one-step time delay

Another model of WTS, which neglects the external noise and considers the one-step time delay, is rebuilt in Fig. 6. Regarding the driving torque \(T_{a} /n_{g}\) as the input and \(\omega_{g}\) as the output, the transfer function of the WTS model shown in Fig. 6 is derived as follows:

$$H_{wts}^{delay} = \frac{T \cdot z}{{J_{s} \cdot z^{2} + \left( {T \cdot k_{L} + J_{t} - 2J_{s} } \right) \cdot z + J_{s} - J_{t} }}$$
(13)
Fig. 6
figure 6

Discrete model of WTS with the one-step time delay considered

Full size image

Obviously, the characteristic equation of this WTS model is different from that of the WT model because of the one-step time delay. Then, the stability condition of the WTS model considering the one-step time delay is derived by the Routh criterion:

$$J_{s} > \frac{{J_{t} }}{2} + \frac{{T \cdot k_{L} }}{4}$$
(14)

By comparing (14) with (11), it can be observed that the stability condition of the WTS with time delay becomes relevant to the inertia of WTS \(J_{s}\). Moreover, considering that the magnitude of \(T \cdot k_{L} /4\) is usually much smaller than that of \(J_{t} /2\), the stability condition (14) can be simplified as the following formula by omitting the term of \(T \cdot k_{L} /4\),

$$J_{t} /J_{s} < 2$$
(15)

According to the above stability analysis, it can be concluded that the instability of WTS is caused by the time delay of acceleration observation rather than external noise. When the inertia \(J_{t}\) greater than two times \(J_{s}\) is compensated, the WTS applying the differential-based acceleration observation is unstable even if there is no external noise.

4 Improved inertia compensation scheme based on deviation mitigation

Based on the stability analysis of WTS, the deviation of time domain response between WTS and WT resulted from the one-step time delay of acceleration observation is further discussed and mitigated by the improved inertia compensation scheme.

4.1 Modeling of response deviation between WTS and WT

The response deviation between WTS and WT is depicted via time domain response analysis. By regarding the torque difference \(T_{a} (k)/n_{g} - T_{g} (k)\) as the input \(r(k)\) and \(\omega_{g} (k)\) as the output \(c(k)\), the open-loop systems of WTS and WT are obtained, as illustrated in Fig. 7 and correspondingly their transfer functions in time domain are derived as follows:

$$c_{wts} (k + 1) - (1 + m) \cdot c_{wts} (k) + m \cdot c_{wts} (k - 1) = n_{1} \cdot r(k)$$
(16)
$$c_{wt} (k + 1) - c_{wt} (k) = n_{2} \cdot r(k)$$
(17)

where \(m = (J_{s} - J_{t} )/J_{s}\), \(n_{1} = T/J_{s}\) and \(n_{2} = T/J_{t}\) (m < 0, 0 < n 2 < n 1). Let \(r(k)\) be the pulse input and the initial conditions be zero. The pulse responses of the two systems are given as follows:

$$c_{wts} (k) = n_{2} \cdot u(k){\kern 1pt} - {\kern 1pt} \left( {\frac{{J_{s} - J_{t} }}{{J_{s} }}} \right)^{k} \cdot n_{2} \cdot u(k){\kern 1pt}$$
(18)
$$c_{wt} (k) = n_{2} \cdot u(k)$$
(19)

where u(k) is the unit step function. By comparing (18) with (19), it is observed that the pulse response of WTS can be decomposed into two response components. The first component is identical with \(c_{wt} (k)\), while the second one is unexpected and defined as the deviation response:

$$c_{d} (k) = {\kern 1pt} \left( {\frac{{J_{s} - J_{t} }}{{J_{s} }}} \right)^{k} \cdot n_{2} \cdot u(k)$$
(20)

which manifests as an exponential sequence. When \(J_{t} /J_{s} \ge 2\), i.e., the stability condition (15) is not satisfied, the deviation response \(c_{d} (k)\) is divergent and leads to the instability of WTS. Therefore, only if the divergent deviation \(c_{d} (k)\) is mitigated, the WTS is stable and replicates the dynamic response similar to WT.

Fig. 7
figure 7

Open-loop diagram of WTS and WT

Full size image

4.2 Design of the filter based on deviation mitigation

Note that the deviation response defined in (20) is a regular sequence, which is amplified at each step. According to this law, a first-order digital filter is therefore selected to mitigate the deviation response in discrete time domain and expressed as follows:

$$\hat{c}(k) = \alpha_{d} \cdot \hat{c}(k - 1) + \beta_{d} \cdot \hat{r}(k)$$
(21)

where \(\hat{r}(k)\) is the input; \(\hat{c}(k)\) is the output, \(\beta_{d}\) and \(\alpha_{d}\) are the coefficients of the first-order filter.

While filtering away the deviation response, the designed filter should not modify the expected response component \(c_{wt} (k)\). Hence, the filter must satisfy the condition that \(\text{when} \; \hat{r}(k) = c_{real} (k), \; \mathop {\lim }\limits_{k \to \infty } \hat{c}(k) = \mathop {\lim }\limits_{k \to \infty } c_{wt} (k).\) Then, (21) is rewritten as

$$\mathop {\lim }\limits_{k \to \infty } \hat{c}(k) = \alpha_{d} \cdot \mathop {\lim }\limits_{k \to \infty } \hat{c}(k - 1) + \beta_{d} \cdot \mathop {\lim }\limits_{k \to \infty } \hat{r}(k)$$
(22)

Assuming that \(\mathop {\lim }\limits_{k \to \infty } c(k - 1) = \mathop {\lim }\limits_{k \to \infty } c(k),\) it is obtained that:

$$\mathop {\lim }\limits_{k \to \infty } c_{wt} (k) = \alpha_{d} \cdot \mathop {\lim }\limits_{k \to \infty } c_{wt} (k) + \beta_{d} \cdot \mathop {\lim }\limits_{k \to \infty } c_{wt} (k)$$
(23)

Dividing out \(\mathop {\lim }\limits_{k \to \infty } c_{wt} (k)\)on both sides of (23), a constraint for the coefficients of the filter is derived from (23):

$$\beta_{d} = 1 - \alpha_{d}$$
(24)

Therefore, the expression of the filter can be rewritten as:

$$\hat{c}(k) = \alpha_{d} \cdot \hat{c}(k - 1) + (1 - \alpha_{d} ) \cdot \hat{r}(k)$$
(25)

Using z transform, the transfer function of the first-order filter for deviation mitigation is then obtained:

$$H_{d} (z) = \frac{{z(1 - \alpha_{d} )}}{{z - \alpha_{d} }}$$
(26)

As illustrated in Fig. 8, the designed first-order filter is added in the torque compensation loop and the open-loop transfer function of WTS is modified as:

$$\begin{aligned} &c^{\prime}_{wts} (k + 2) - [\alpha_{d} + m(1 - \alpha_{d} ) + 1] \cdot c^{\prime}_{wts} (k + 1) + \\&{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [\alpha_{d} + m(1 - \alpha_{d} )] \cdot c^{\prime}_{wts} (k) = n_{1} \cdot [r^{\prime}(k + 1) - \alpha_{d} \cdot r^{\prime}(k)] \hfill \\ \end{aligned}$$
(27)
Fig. 8
figure 8

Open-loop diagram of WTS with the first-order filter employed

Full size image

Then, the pulse response of WTS with zero initial condition is obtained as:

$$\begin{aligned} c^{\prime}_{wts} (k) &= n_{2} \cdot u(k){\kern 1pt} - \left( {\beta \cdot n_{2} + \alpha_{d} {\kern 1pt} \cdot n_{1} } \right) \cdot \beta^{k - 1} \cdot u(k) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= c_{wt} (k) - c^{\prime}_{d} (k) \hfill \\ \end{aligned}$$
(28)

where

$$\beta = \alpha_{d} + \left( {\frac{{J_{s} - J_{t} }}{{J_{s} }}} \right) \cdot (1 - \alpha_{d} )$$
(29)

It can be inferred from (29) that the pulse response of WTS still consists of two response components. The first one is identical with the expected response \(c_{wt} (k)\). The second one is a new exponential deviation \(c^{\prime}_{d} (k)\), whose base \(\beta\) is different from that of \(c_{d} (k)\). Compared with the base of \(c_{d} (k)\) determined by the fixed structural parameters (i.e. J t and J s ), the base of \(c^{\prime}_{d} (k)\) is adjustable since the filter coefficient \(\alpha_{d}\) is introduced. Note that when \(\left| \beta \right| < 1,\; \mathop {\lim }\limits_{k \to \infty } c^{\prime}_{d} (k) = 0.\)

That is to say, when \(\left| \beta \right| < 1\), the new deviation is mitigated because it converges to zero with time. According to (29), the convergence condition of \(c^{\prime}_{d} (k)\) can be rearranged as

$$\frac{{J_{t} - 2J_{s} }}{{J_{t} }} < \alpha_{d} < 1$$
(30)

Therefore, by employing the first-order filter and setting its coefficient \(\alpha_{d}\) according to (30), the deviation response \(c^{\prime}_{d} (k)\) is mitigated and the pulse response of WTS converges to that of WT. Furthermore, since a complex discrete input can be regarded as a linear weighted combination of pulse signals, the aforementioned pulse response analysis in time domain can be directly extended to the response of WTS excited by a complex input of torque difference.

4.3 Stability analysis on WTS with the filter employed

The discrete model of WTS with the first-order filter employed is drawn in Fig. 9 and its closed-loop transfer function is derived as:

$$H_{wts}^{filter} = \frac{{T \cdot \left( {z - \alpha_{d} } \right)}}{{J_{s} \cdot z^{2} + \left( {k_{L} T - \beta J_{s} - J_{s} } \right) \cdot z + \beta J_{s} - k_{L} T\alpha_{d} }}$$
(31)
Fig. 9
figure 9

Discrete model of WTS with the filter employed

Full size image

Using the Routh criterion, the stability condition is obtained as:

$$\frac{{J_{t} - 2J_{s} + k_{L} T/2}}{{J_{t} - k_{L} T/2}} < \alpha_{d} < 1$$
(32)

Considering that the magnitude of \(k_{L} T/2\) is much smaller than that of \(J_{t}\) or \(J_{s}\), the term of \(k_{L} T/2\) can be omitted. Accordingly, the stability condition of the closed-loop WTS is approximately equivalent to the convergence condition (30) of deviation response \(c^{\prime}_{d} (k)\). Therefore, when the designed filter is applied, the response of WTS is not only stable but also convergent to that of WT.

5 Simulation and experimental validation

In this section, the effects of time delay and external noise are comparatively studied by simulations. Then, experiments are conducted to verify the stability of WTS with the proposed inertia compensation scheme.

5.1 Simulation studies of WTS

Because electromagnetic response is much faster than mechanical response, a simulation model of WTS, in which the electric system with fast dynamics is neglected, is built in MATLAB/Simulink, as depicted in Fig. 10. The specifications of the simulation model are listed in Table 1. The generator torque is regulated by:

$$T_{g} = k_{opt} \cdot \omega_{g}^{2}$$
(33)

which is a commonly used control strategy for maximum power point tracking (MPPT) of wind turbines, known as the optimal torque control [23]. \(k_{opt}\) is the optimal torque gain.

Fig. 10
figure 10

Simulation model of WTS established in MATLAB/Simulink

Full size image
Table 1 The specifications of the simulation model of WTS
Full size table

Simulation case I: First, the first-order filter is not employed and the simulated moment of inertia \(J_{t}\) is set to \(3J_{s}\) (larger than \(2J_{s}\)). Additionally, the external noise is not added and a step wind speed is applied as the input. The simulation result plotted in Fig. 11 shows that because the stability condition is not satisfied, the torque compensation loop is oscillating, which consequently leads to the instability of WTS. It is also validated that when \(J_{t}\) greater than two times \(J_{s}\) is compensated, the WTS applying the differential-based acceleration observation is unstable even if there is no external noise, which agrees with the stability condition derived in Section 3. Note that this case cannot be conducted by WTS experiments since signal noise is actually unavoidable.

Fig. 11
figure 11

Simulation case I: WTS without filter and J t is set larger than 2J s

Full size image

Simulation case II: Then, the first-order filter with \(\alpha_{d}\) set to 0.9 is utilized and the simulated moment of inertia \(J_{t}\) remains \(3J_{s}\). The value of \(\alpha_{d}\) satisfies the convergence condition of deviation response expressed as (30). According to the simulation result plotted in Fig. 12, it can be observed that the rotational speed of WTS (black solid line) can stably track that of WT (red solid line) and finally converge to it. This case verifies that by employing the improved inertia compensation scheme based on deviation mitigation, the WTS is able to stably and accurately replicate the dynamic and steady behaviors of WTs.

Fig. 12
figure 12

Simulation case II: WTS with filter and J t is set larger than 2J s

Full size image

Simulation case III: Next, a pulse noise is added to the rotational speed measurement of WTS at 2s and correspondingly the simulation result is shown in Fig. 13. After the disturbance, the compensation torque immediately converges and the rotational speed of WTS (zoomed in within blue dotted circle) deviates slightly from that of WT (red solid line). It is demonstrated that although the external noise in rotational speed measurement affects the accuracy of WTS to some extent, it cannot lead to the instability of WTS when the proposed inertia compensation scheme is employed.

Fig. 13
figure 13

Simulation case III: the speed measurement of WTS is disturbed by a pulse noise at 2s

Full size image

Simulation case IV: Although WTs with larger \(J_{t}\) can be stably simulated by increasing \(\alpha_{d}\), \(\alpha_{d}\) should not be excessively close to 1.0 because of the simulation accuracy of WTS. And in this paper, \(\alpha_{d}\) is recommended to be smaller than 0.95 in accordance with the discrete time step (10 ms). If \(\alpha_{d}\) is set too large (e.g., 0.98), the amplitude-frequency response (AFR) of the torque compensation loop at high frequency band is attenuated too much and the transient response of \(T_{comp}\) is slowed down. As a result, the rotational speed of WTS significantly deviates from that of WT though it is stable, as shown in Fig. 14.

Fig. 14
figure 14

Simulation case IV: WTS with α d set to 0.98

Full size image

5.2 System implementation of WTS

The WTS-based WECS in this paper is built according to the structure of practical WECS with full-power converter where a cascaded control structure through two control loops is commonly adopted [1, 22]:

  1. 1)

    The aerodynamic-mechanical part and outer-loop control. The outer-loop control concerns the regulation of wind power generation and provides the generator torque reference as the input to the generator controller (inner-loop control). Because of the slow mechanical behavior of WT, the outer-loop control can be implemented by Programmable Logic Controller (PLC) and its cycle is usually selected as tens of milliseconds.

  2. 2)

    The electric part and inner-loop control. The generator control regulates the generator torque according to the torque reference by modulating the rectifier. Besides, the active/reactive power to the grid is regulated by modulating the inverter. Because the electric part and inner-loop control are not discussed in this paper, they are directly accomplished by industrial converters, as commonly implemented in practical WECSs.

The specifications of the WTS test bench designed above are listed in Table 2. Its structure is illustrated in Fig. 15, including the following major components:

Table 2 The specifications of the WTS test bench
Full size table
Fig. 15
figure 15

Hardware structure of the WTS-based WECS

Full size image
  1. 1)

    A real-time digital control system (DCS) based on Beckhoff PLC. In DCS, the wind data generation, the acceleration observation, the aerodynamic torque calculation, the proposed inertia compensation scheme and the wind turbine control strategy (i.e., the optimal torque control (33)) are executed every 10ms, and correspondingly the motor torque T s and generator torque T g are periodically outputted as control references to the motor drive and rectifier.

  2. 2)

    A three phase induction motor (IM) driven by a VACON variable-frequency drive. The IM torque is controlled to follow up the torque reference T s received from the DCS.

  3. 3)

    A permanent magnet synchronous generator (PMSG) coupled with a full-power converter (including a rectifier and an inverter implemented based on VACON drive). The rectifier receives and executes the generator torque T g . The inverter regulates the dc-link voltage according to the voltage reference which is set to a constant value.

  4. 4)

    A host computer for recording experimental data.

5.3 Experimental validation

To test the stability and effectiveness of WTS applying the proposed inertia compensation scheme, the following experimental cases excited by a step wind speed or turbulence are conducted:

Experimental case I: First, the first-order filter is not employed and the simulated moment of inertia \(J_{t}\) is set to the value of \(3J_{s}\). As plotted in Fig. 16, the severe oscillation of the compensation torque and rotational speed indicates that the WTS is unstable, which is consistent with the stability condition derived in Section 3. Besides, it needs to be pointed out that the oscillating curves are characterized by an asymptotic divergence rather than a random noise disturbance.

Fig. 16
figure 16

Experimental case I: WTS without filter and J t is set to 3J s

Full size image

Experimental case II: Then, the first-order filter is added in the torque compensation loop and its coefficient is determined as 0.9 that satisfies the convergence condition of deviation response (30). As shown in Fig. 17, the stable trajectories demonstrate that the filter designed for mitigating the deviation response does work and the WTS with \(J_{t} = 3J_{s}\) is stabilized.

Fig. 17
figure 17

Experimental test II: WTS with filter and J t is set to 3J s

Full size image

Experimental case III: In order to test the inertia effect of the WTS simulating different values of \(J_{t}\), more experiments, in which \(J_{t} /J_{s}\) is set at various values (from 1.0 to 5.0) and correspondingly \(\alpha_{d}\) is adjusted by (30), are carried out. The dynamic responses excited by the same step wind speed are drawn in Fig. 18. It is observed that the rise time gradually increases with the simulated \(J_{t}\). Additionally, after the dynamic process, the WTS with different values of \(J_{t}\) reaches the same rotational speed. Therefore, the inertia effect, especially the slow dynamic behavior due to larger inertia, is stably replicated by applying the proposed inertia compensation scheme.

Fig. 18
figure 18

Experiments III: rotational speed trajectories of the WTS with different moment of inertia J t

Full size image

Experimental case IV: Furthermore, the dynamic behavior of WTS with different values of \(J_{t}\) in response to turbulent wind is compared. As shown in Fig. 19, the rotational speed trajectories of the WTS differ for \(J_{t}\). Moreover, the larger is the moment of inertia \(J_{t}\) simulated by the WTS, the slower the rotational speed in response to turbulence. In addition, the rotational speed trajectory (red solid line) calculated by the WT model (3) with \(J_{t} = 5J_{s}\) is also plotted in Fig. 19. It is apparent from Fig. 19 that for the same moment of inertia \(J_{t}\), the rotational speed trajectory of WTS approximates to that of WT. This means that the proposed inertia compensation scheme based on deviation mitigation can replicate the slow mechanical dynamics of large-inertia WTs stably and accurately.

Fig. 19
figure 19

Experiments IV: rotational speed trajectories of the WTS and WT in response to turbulence

Full size image

6 Conclusion

To verify the control and optimization of WECS, the WTS should reproduce the dynamic behavior similar to WTs. However, the applicability of WTS to simulating large-inertia WTs is limited by the instability of WTS. In this paper, the instability of WTS applying the inertia compensation scheme is analyzed and interpreted as the consequence of the one-step time delay of acceleration observation. By establishing the linear discrete model of WTS considering time-delay and analyzing its stability condition, an inertia compensation scheme, in which a first-order filter for eliminating deviation response is added to the torque compensation loop, is proposed for stabilizing WTS. Without changing the inner loop control and experimental hardware, the WTS-based test bench can conveniently and economically implement the proposed inertia compensation scheme and reproduce the slow mechanical dynamics of WTs.