Abstract
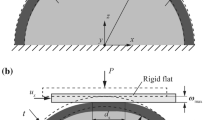
Finite element analysis is used to investigate an elastic-plastic coated spherical contact in full stick contact condition under combined normal and tangential loading. Sliding inception is associated with a loss of tangential stiffness. The effect of coating thickness on the static friction coefficient is intensively investigated for the case of hard coatings. For this case, with the increase in coating thickness, the static friction coefficient first increases to its maximum value at a certain coating thickness, thereafter decreases, and eventually levels off. The effect of the normal load and material properties on this behavior is discussed. Finally, a model for the static friction coefficient as a function of the coating thickness is provided for a wide range of material properties and normal loading.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Eriksson M, Bergman F, Jacobson S. On the nature of tribological contact in automotive brakes. Wear252(1–2): 26–36 (2002)
Ost W, De Baets P, Degrieck J. The tribological behaviour of paper friction plates for wet clutch application investigated on SAE#II and pin-on-disk test rigs. Wear249(5–6): 361–371 (2001)
Srivastava N, Haque I. Transient dynamics of metal V-belt CVT: Effects of band pack slip and friction characteristic. Mech Mach Theory43(4): 459–479 (2008)
Salib J, Kligerman Y, Etsion I. A model for potential adhesive wear particle at sliding inception of a spherical contact. Tribol Lett30(3): 225–233 (2008)
Holmberg K, Andersson P, Erdemir A. Global energy consumption due to friction in passenger cars. Tribol Int47: 221–234 (2012)
Hintermann H E. Adhesion, friction and wear of thin hard coatings. Wear100(1–3): 381–397 (1984)
Holmberg K, Ronkainen H, Matthews A. Tribology of thin coatings. Ceram Int26(7): 787–795 (2000)
Hogmark S, Jacobson S, Larsson M. Design and evaluation of tribological coatings. Wear246(1–2): 20–33 (2000)
Holmberg K, Ronkainen H, Laukkanen A, Wallin K. Friction and wear of coated surfaces - scales, modelling and simulation of tribomechanisms. Surf Coat Technol202(4–7): 1034–1049 (2007)
Greenwood J, Williamson J B P. Contact of nominally flat surfaces. Proc Roy Soc A: Math, Phys Eng Sci295(1442): 300–319 (1966)
Keer L M, Kim S H, Eberhardt A W, Vithoontien V. Compliance of coated elastic bodies in contact. Int J Solids Struct27(6): 681–698 (1991)
Garjonis J, Kacianauskas R, Stupak E, Vadluga V. Investigation of contact behaviour of elastic layered spheres by FEM. Mechanika3(77): 5–12 (2009)
Goltsberg R, Etsion I. A universal model for the load–displacement relation in an elastic coated spherical contact. Wear322–323: 126–132 (2015)
Goltsberg R, Etsion I. Contact area and maximum equivalent stress in elastic spherical contact with thin hard coating. Tribol Int93: 289–296 (2016)
Goltsberg R, Etsion I, Davidi G. The onset of plastic yielding in a coated sphere compressed by a rigid flat. Wear271(11–12): 2968–2977 (2011)
Chen Z, Goltsberg R, Etsion I. Yield modes in a coated spherical contact. Tribol Int120: 309–316 (2018)
Goltsberg R, Etsion I. A model for the weakening effect of very thin hard coatings. Wear308(1–2): 10–16 (2013)
Huang X, Kasem H, Shang H F, Shao T M, Etsion I. Experimental study of a potential weakening effect in spheres with thin hard coatings. Wear296(1–2): 590–597 (2012)
Eid H, Joshi N, McGruer N E, Adams G G. A model of contact with adhesion of a layered elastic-plastic microsphere with a rigid flat surface. J Tribol133(3): 031406 (2011)
Chen L, Guo Z J, Joshi N, Eid H, Adams G G, McGruer N E. An improved SPM-based contact tester for the study of microcontacts. J Micromech Microeng22(4): 045017 (2012)
Nguyen H V, He J Y, Helland T, Kristiansen H, Aasmundtveit K E. Electrical characterization of individual metal-coated polymer spheres used in isotropic conductive adhesives. J Appl Polym Sci133(31): 43764 (2016)
Bazilchuk M, Pettersen S R, Kristiansen H, Zhang Z L, He J Y. Electromechanical characterization of individual micronsized metal coated polymer particles. J Appl Phys119(24): 245102 (2016)
Chen Z, Goltsberg R, Etsion I. Plasticity evolution in a coated sphere compressed by a rigid flat. Tribol Int98: 116–124 (2016)
Chen Z, Goltsberg R, Etsion I. A universal model for a frictionless elastic-plastic coated spherical normal contact with moderate to large coating thicknesses. Tribol Int114: 485–493 (2017)
Ronen S, Goltsberg R, Etsion I. A comparison of stick and slip contact conditions for a coated sphere compressed by a rigid flat. Friction5(3): 326–338 (2017)
Kogut L, Etsion I. A semi-analytical solution for the sliding inception of a spherical contact. J Tribol125(3): 499–506 (2003)
Eriten M, Polycarpou A A, Bergman L A. Physics-based modeling for partial slip behavior of spherical contacts. Int J Solids Struct47(18–19): 2554–2567 (2010)
García J M, Martini A. Measured and predicted static friction for real rough surfaces in point contact. J Tribol134(3): 031501 (2012)
Wu A Z, Shi X, Polycarpou A A. An elastic-plastic spherical contact model under combined normal and tangential loading. J Appl Mech79(5): 051001 (2012)
Wu A Z, Shi X. Numerical investigation of adhesive wear and static friction based on the ductile fracture of junction. J Appl Mech80(4): 041032 (2013)
Shi X. On slip inception and static friction for smooth dry contact. J Appl Mech81(12): 121005 (2014)
Brizmer V, Kligerman Y, Etsion I. Elastic-plastic spherical contact under combined normal and tangential loading in full stick. Tribol Lett25(1): 61–70 (2007)
Zolotarevskiy V, Kligerman Y, Etsion I. The evolution of static friction for elastic-plastic spherical contact in pre-sliding. J Tribol133(3): 034502 (2011)
Bhagwat P, Sista B, Vemaganti K. A computational study of the effects of strain hardening in micro-asperity friction models. Tribol Lett65(4): 154 (2017)
Zhao B, Zhang S, Keer L M. Spherical elastic-plastic contact model for power-law hardening materials under combined normal and tangential loads. J Tribol139(2): 021401 (2017)
Etsion I. Revisiting the Cattaneo-Mindlin Concept of interfacial slip in tangentially loaded compliant bodies. J Tribol132(2): 020801 (2010)
Ovcharenko A, Halperin G, Etsion I. In situ and real-time optical investigation of junction growth in spherical elasticplastic contact. Wear264(11–12): 1043–1050 (2008)
ANSYS® Academic Teaching Mechanical and CFD, Release 18.1, Help System. ANSYS Documentation/Mechanical APDL/Command References/XXIII. V Commands/VROTAT. ANSYS, Inc.
ANSYS® Academic Teaching Mechanical and CFD, Release 18.1, Help System. ANSYS Documentation/Mechanical APDL/Contact Technology Guide/3. Surface-to-Surface Contact (Pair-Based)/3.6 Defining the Target Surface/3.6.1 Pilot nodes. ANSYS, Inc.
Goltsberg R, Levy S, Kligerman Y, Etsion I. Strengthening Effect of soft thin coatings. J Tribol140(6): 064501 (2018)
Acknowledgment
This paper is part of IEA AMT IA technical activities.
Author information
Authors and Affiliations
Corresponding author
Additional information
Zhou CHEN. He received his bachelor degree in mechanical engineering in 2014 from Harbin Institute of Technology, China. He is currently a Ph.D student in the Department of Mechanical Engineering, Technion, Israel. His research interests include contact mechanics and coatings.
Izhak ETSION. He received his Ph.D degree in 1974 from Technion- Israel Institute of Technology. Since then he was a faculty at the Department of Mechanical Engineering where he is currently a professor emeritus. His research interests are in hydrodynamic lubrication, surface texturing, contact mechanics, nano-tribology and bio-tribology. He has published over 200 papers on various aspects of tribology and holds 15 patents. He is the founder of Surface Technologies Ltd. that developed the laser surface texturing (LST) technology for friction and wear reduction. His honors include fellow of the ASME (1999), fellow of the STLE (2001), the STLE 2005 International Award and the ASME 2016 Mayo D. Hersey Award.
Rights and permissions
Open Access: The articles published in this journal are distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chen, Z., Etsion, I. Model for the static friction coefficient in a full stick elastic-plastic coated spherical contact. Friction 7, 613–624 (2019). https://doi.org/10.1007/s40544-018-0251-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40544-018-0251-5