Abstract
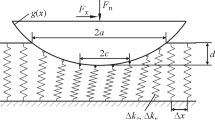
The influence of out-of-plane oscillations on friction is a well-known phenomenon that has been studied extensively with various experimental methods, e.g., pin-on-disk tribometers. However, existing theoretical models have yet achieved only qualitative correspondence with experiment. Here we argue that this may be due to the system dynamics (mass and tangential stiffness) of the pin or other system components being neglected. This paper builds on the results of a previous study [19] by taking the stiffness and resulting dynamics of the system into account. The main governing parameters determining macroscopic friction, including a dimensionless oscillation amplitude, a dimensionless sliding velocity and the relation between three characteristic frequencies (that of externally excited oscillation and two natural oscillation frequencies associated with the contact stiffness and the system stiffness) are identified. In the limiting cases of a very soft system and a very stiff system, our results reproduce the results of previous studies. In between these two limiting cases there is also a resonant case, which is studied here for the first time. The resonant case is notable in that it lacks a critical sliding velocity, above which oscillations no longer reduce friction. Results obtained for the resonant case are qualitatively supported by experiments.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Siegert K, Ulmer J. Superimposing ultrasonic waves on tube and wire drawing. J Eng Mater Technol 123(724): 517–523 (2000)
Egashira K, Mizutani K, Nagao T. Ultrasonic vibration drilling of microholes in glass. CIRP Ann Technol 51(1): 339–342 (2002)
Godfrey D. Vibration reduces metal to metal contact and causes an apparent reduction in friction. ASLE Trans 10(2): 183–192 (1967)
Fridman H D, Levesque P. Reduction of static friction by sonic vibrations. J Appl Phys 30(10): 1572–1575 (1959)
Broniec Z, Lenkiewicz W. Static friction processes under dynamic loads and vibration. Wear 80(3): 261–271 (1982)
Littmann W, Storck H, Wallaschek J. Sliding friction in the presence of ultrasonic oscillations: superposition of longitudinal oscillations. Arch Appl Mech 71(8): 549–554 (2001)
Teidelt E. Oscillating contacts: Friction induced motion and control of friction. Ph.D. Thesis. Berlin (Germany): Technische Universität Berlin, 2015.
Popov V L, Wetter R. Symmetry breaking as a general design principle of oscillation-based methods for fixation and manipulation of nano-objects. Advanced Biomaterials and Devices in Medicine 3(1): 10–18 (2016)
Weishaupt W. Reibungsverminderung durch mechanische Schwingungen. Tech Mess 11: 345–348 (1976)
Goto H, Ashida M, Terauchi Y. Effects of ultrasonic vibration on the wear characteristics of a carbon steel: Analysis of the wear mechanism. Wear 94(1): 13–27 (1984)
Chowdhury M A, Helali M M. The effect of frequency of vibration and humidity on the coefficient of friction. Tribol Int 39(9): 958–962 (2006)
Chowdhury M A, Helali M M. The effect of amplitude of vibration on the coefficient of friction for different materials. Tribol Int 41(4): 307–314 (2008)
Popov V L, Starcevic J, Filippov A E. Influence of ultrasonic in-plane oscillations on static and sliding friction and intrinsic length scale of dry friction processes. Tribol Lett: 39(1): 25–30 (2010)
Teidelt E, Starcevic J, Popov V L. Influence of ultrasonic oscillation on static and sliding friction. Tribol Lett 48(1): 51–62 (2012)
Milahin N, Li Q, Starcevic J. Influence of the normal force on the sliding friction under ultrasonic oscillations. Facta Univ Ser Mech Eng 13(1): 27–32 (2015)
Milahin N. Robuste Einflussparameter für Reibung und Oberflä-chenmodifizierung unter Einfluss von Ultraschall. Ph.D. Thesis. Berlin (Germany): Technische Universität Berlin, 2016.
Nguyen H X, Teidelt E, Popov V L, Fatikow S. Dynamical tangential contact of rough surfaces in stick-slip microdrives: modeling and validation using the method of dimensionality reduction. Physical Mesomechanics 17(4): 304–310 (2014)
Cabboi A, Putelat T, Woodhouse J. The frequency response of dynamic friction: enhanced rate-and-state models. Journal of the Mechanics and Physics of Solids 92: 210–236 (2016)
Popov M, Popov V L, Popov N V. Reduction of friction by normal oscillations. I. Influence of contact stiffness. Friction 5(1): 45–55 (2017)
Popov M. Critical velocity of controllability of sliding friction by normal oscillations in viscoelastic contacts. Facta Universitatis, Series: Mechanical Engineering 14(3): 335–341 (2016)
Acknowledgements
The authors would like to thank Juliane Wallendorf and Qiang Li for their help with preparing figures for the paper. This work was supported in part by Tomsk State University Academic D.I. Mendeleev Fund Program (No. 8.2.19.2015).
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is published with open access at Springerlink.com
Xinyu MAO. Double master degree candidate in the majors of Mechanical Engineering at the Tsinghua University and Engineering Science at the Berlin University of Technology. He obtained his bachelor degree in mechanical engineering at Tsinghua University in 2014. His research interests include tribological simulations, especially friction and wear (fretting) under the action of vibration.
Valentin L. POPOV. Full professor at the Berlin University of Technology, studied physics (1976–1982) and obtained his doctorate in 1985 from the Moscow State Lomonosov University. He worked at the Institute of Strength Physics of the Russian Academy of Sciences. After a guest professorship in the field of theoretical physics at the University of Paderborn (Germany) from 1999 to 2002, he has headed the Department of System Dynamics and the Physics of Friction of the Institute of Mechanics at the Berlin University of Technology. His areas of interest include tribology, nanotribology, tribology at low temperatures, biotribology, the influence of friction through ultrasound, numerical simulation of frictional processes, research regarding earthquakes, as well as topics related to materials science such as the mechanics of elastoplastic media with microstructures, strength of metals and alloys, and shape memory alloys. He has published over 100 papers in leading international journals during the past 5 years. He is the author of the book “Contact Mechanics and Friction: Physical Principles and Applications” which appeared in three German, two English, Chinese, and Russian editions and co-author of the book on “Method of Dimensionality Reduction in Contact Mechanics and Friction” which appeared in German, English and Chinese editions. He is the joint editor of international journals and regularly organizes international conferences and workshops on diverse tribological themes. He is a member of the Scientific Council of the German Tribological Society. He has intensively collaborated with many industrial corporations and possesses experience in implementing the results of scientific research in industrial applications.
Jasminka STARCEVIC. She is the head of experimental laboratories at the Institute of Mechanics at the Berlin University of Technology. She studied mechanical engineering at the Berlin University of Technology and obtained the degree of Diplom- Ingeneiur in 1997 and the doctorate in 2008. She is a co-author of 25 papers in international journals. Her research interests include physics of friction, active control of friction by ultrasonic oscillations, tribospectroscopy, as well as development of methods for earthquake prediction. She has intensively collaborated with many industrial corporations and possesses experience in implementing the results of scientific research in industrial applications.
Mikhail POPOV. He obtained the bachelor degree in computer science from the Freie Universität Berlin in 2011 and the master degree in engineering science from the Tomsk Polytechnic University and Berlin Technical University in 2016. Currently he is a research assistant at the Tomsk Polytechnic University and Berlin University of Technology. His research interests include efficient numerical methods in tribology, rubber friction, as well as friction and damping under the influence of oscillations.
Rights and permissions
Open Access: The articles published in this journal are distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mao, X., Popov, V.L., Starcevic, J. et al. Reduction of friction by normal oscillations. II. In-plane system dynamics. Friction 5, 194–206 (2017). https://doi.org/10.1007/s40544-017-0146-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40544-017-0146-x