Skip to main content
SpringerLink
Log in

Numerical Laplace inverse based on operational matrices for fractional differential equations

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

In this paper, an effective numerical method for determining the numerical inversion of the Laplace transform is presented, and its applicability to fractional differential equations is also investigated. To show the effectiveness and simplicity of the suggested technique, numerical examples are provided. Through error tables and graphical representations, the suggested numerical technique shows high accuracy. This proposed numerical approach is simple and ideal for MATLAB programming.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data Availability

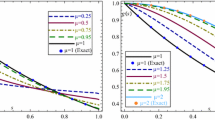
All the data used for the numerical simulations and comparison purpose have been reported in the tables included and visualized in the graphical illustrations and nothing is left.

References

  1. Abu Arqub O (2018) Numerical solutions for the Robin time-fractional partial differential equations of heat and fluid flows based on the reproducing kernel algorithm. Int J Num Methods for Heat & Fluid Flow 28(4):828–856

    Article  Google Scholar 

  2. Abu Arqub O, Al-Smadi, M (2010) Numerical solutions of Riesz fractional diffusion and advection-dispersion equations in porous media using iterative reproducing kernel algorithm. J Porous Med, 23(8),

  3. Abu Arqub O (2020) Numerical simulation of time-fractional partial differential equations arising in fluid flows via reproducing Kernel method. Int J Num Methods for Heat & Fluid Flow 30(11):4711–4733

    Article  Google Scholar 

  4. Aznam SM, Hussin A (2012) Numerical method for inverse Laplace transform with Haar Wavelet operational matrix. Malaysian Journal of Fundamental and Applied Sciences, 8(4)

  5. Aruldoss R, Balaji K (2022) Numerical Inversion of Laplace Transform via Wavelet Operational Matrix and Its Applications to Fractional Differential Equations. Int J Appl Comput Math, 8(16), (2022)

  6. Aruldoss R, Devi RA, Krishna PM (2021) An expeditious wavelet-based numerical scheme for solving fractional differential equations. Comput Appl Math 40:1–14

    Article  MathSciNet  Google Scholar 

  7. Aruldoss R, Balaji K (2023) A wavelet-based collocation method for fractional Cahn-Allen equations. J Fractional Calculus and Appl 14(1):26–35

    MathSciNet  Google Scholar 

  8. Aruldoss R, Balaji K (2023) A novel iterative algorithm for solving fractional differential equations 12(1):768–777

    Google Scholar 

  9. Aruldoss R, Jasmine G (2020) Numerical solutions of time fractional nonlinear partial differential equations using yang transform combined with variational iteration method. Global J Pure and Appl Math 16(2):249–260

    Google Scholar 

  10. Aruldoss R, Jasmine GA (2022) Wavelet collocation method for some fractional models. Ratio Mathematica , 43(2),

  11. Aruldoss R, Jasmine G (2023) A wavelet based approach for numerical inversion of a a generalized integral transform. Indian J Natural Sci 14(77):54485–54497

    Google Scholar 

  12. Aruldoss R, Balaji K (2023) Applications of wavelet operational matrix for numerical inversion of Laplace transform. Indian J Natural Sci 14(77):54523–54531

    Google Scholar 

  13. Arikoglu A, Ozkol I (2007) Solution of fractional differential equations by using differential transform method. Chaos, Solitons & Fractals 34(5):1473–1481

    Article  ADS  MathSciNet  Google Scholar 

  14. Diethelm K, Ford J (2002) Numerical solution of the Bagley-Torvik equation. BIT Numer Math 42(3):490–507

    Article  MathSciNet  Google Scholar 

  15. Diethelm K (2004) The analysis of fractional differential equations: an application-oriented exposition using operators of caputo type. Springer, Berlin

    Google Scholar 

  16. Erturk VS, Momani S, Odibat Z (2008) Application of generalized differential transform method to multi-order fractional differential equations. Commun Nonlinear Sci Numer Simul 13(8):1642–1654

    Article  ADS  MathSciNet  Google Scholar 

  17. Farooq U, Khan H, Baleanu D, Arif M (2019) Numerical solutions of fractional delay differential equations using Chebyshev wavelet method. Comput Appl Math 38(4):1–13

    Article  MathSciNet  Google Scholar 

  18. Garra R (2012) Analytic solution of a class of fractional differential equations with variable coefficients by operational methods. Commun Nonlinear Sci Numer Simul 17(4):1549–1554

    Article  ADS  MathSciNet  Google Scholar 

  19. Hosseini MM (2006) Adomian decomposition method for solution of nonlinear differential algebraic equations. Appl Math Comput 181(2):1737–1744

    MathSciNet  Google Scholar 

  20. Hsiao CH (2014) Numerical inversion of Laplace transform via wavelet in ordinary differential equations. Comput. Methods for Differ. Equs. 2(3):186–194

    MathSciNet  Google Scholar 

  21. Hsiao CH (2014) Numerical inversion of Laplace transform via wavelet in partial differential equations. Num. Methods for Partial Differ. Equs. 30(2):536–549

    Article  MathSciNet  Google Scholar 

  22. Kilicman A, Al Zhour ZAA (2007) Kronecker operational matrices for fractional calculus and some applications. Appl Math Comput 187(1):250–265

    MathSciNet  Google Scholar 

  23. Keskin Y, Karaolu O, Servi S (2011) The approximate solution of high-order linear fractional differential equations with variable coefficients in terms of generalized Taylor polynomials. Math. Comput. Appl. 16(3):617–629

    MathSciNet  Google Scholar 

  24. Kreyszig E (2007) Advanced Engineering Mathematics 8th Edition with Wiley Plus Set, vol 334. John Wiley & Sons, US

    Google Scholar 

  25. Mainardi F (1996) Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos, Solitons & Fractals 7(9):1461–1477

    Article  ADS  MathSciNet  Google Scholar 

  26. Miller KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations. Wiley, US

    Google Scholar 

  27. Mekkaoui T, Hammouch Z (2012) Approximate analytical solutions to the Bagley-Torvik equation by the fractional iteration method. Ann Univ Craiova-Math Comput Sci Series 39(2):251–256

    MathSciNet  Google Scholar 

  28. Miller KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations. Wiley, US

    Google Scholar 

  29. Mishra V, Rani D (2020) Laplace transform inversion using Bernstein operational matrix of integration and its application to differential and integral equations. Proceed-Math Sci 130(1):1–29

    MathSciNet  Google Scholar 

  30. Odibat ZM (2010) A study on the convergence of variational iteration method. Math Comput Model 51(9–10):1181–1192

    Article  MathSciNet  Google Scholar 

  31. Oldham KB, Spanier J (1974) The Fractional Calculus. Academic Press, New York

    Google Scholar 

  32. Mohammadi A, Aghazadeh N, Rezapour S (2019) Haar wavelet collocation method for solving singular and nonlinear fractional time-dependent Emden-Fowler equations with initial and boundary conditions. Math Sci 13(3):255–265

    Article  MathSciNet  Google Scholar 

  33. Podlubny I (1999) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications (Vol. 198). Elsevier,

  34. Raja MAZ, Samar R, Manzar MA, Shah SM (2017) Design of unsupervised fractional neural network model optimized with interior point algorithm for solving Bagley-Torvik equation. Math Comput Simul 132:139–158

    Article  MathSciNet  Google Scholar 

  35. Rahimkhani P, Moeti R (2018) Numerical Solution of the Fractional Order Duffing-van der Pol Oscillator Equation by Using Bernoulli Wavelets Collocation Method. Int J Appl Comput Math 4(2):1–18

    Article  MathSciNet  Google Scholar 

  36. Rahimkhani P, Ordokhani Y, Babolian E (2018) Müntz-Legendre wavelet operational matrix of fractional-order integration and its applications for solving the fractional pantograph differential equations. Num Algorithms 77(4):1283–1305

    Article  Google Scholar 

  37. Rani D, Mishra V (2020) Numerical inverse Laplace transform based on Bernoulli polynomials operational matrix for solving nonlinear differential equations. Results in Phys. 16:102836

    Article  Google Scholar 

  38. Razzaghi M, Yousefi S (2000) Legendre wavelets direct method for variational problems. Math Comput Simul 53(3):185–192

    Article  MathSciNet  Google Scholar 

  39. Razzaghi M, Yousefi S (2001) The Legendre wavelets operational matrix of integration. Int J Syst Sci 32(4):495–502

    Article  MathSciNet  Google Scholar 

  40. Sweis H, Shawagfeh N, Arqub OA (2022) Fractional crossover delay differential equations of Mittag-Leffler kernel: Existence, uniqueness, and numerical solutions using the Galerkin algorithm based on shifted Legendre polynomials. Results in Phys 41:105891

    Article  Google Scholar 

  41. Toan PT, Vo TN, Razzaghi M (2019) Taylor wavelet method for fractional delay differential equations. Engineering with Computers, 1-10,

  42. Ur Rehman M, Khan RA (2011) The Legendre wavelet method for solving fractional differential equations. Commun Nonlinear Sci Numer Simul 16(11):4163–4173

    Article  ADS  MathSciNet  Google Scholar 

  43. Verma A, Kumar M (2020) Numerical solution of Bagley-Torvik equations using Legendre artificial neural network method. Evolu Intell, 1-11,

  44. Wang Y, Fan Q (2012) The second kind Chebyshev wavelet method for solving fractional differential equations. Appl Math Comput 218(17):8592–8601

    MathSciNet  Google Scholar 

  45. Wang Y, Zhu L, Wang Z (2019) Solving the nonlinear variable order fractional differential equations by using Euler wavelets. Comput Model Eng Sci 118(2):339–350

    Google Scholar 

  46. Wu JL, Chen CH, Chen CF (2001) Numerical inversion of Laplace transform using Haar wavelet operational matrices. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications 48(1):120–122

    Article  Google Scholar 

  47. Zhang Y (2009) A finite difference method for fractional partial differential equation. Appl Math Comput 215(2):524–529

    MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the anonymous reviewers for several comments and suggestions which contributed to the improvement of this paper.

Funding

The authors received no financial support for the research, authorship and/or publication of this article.

Author information

Authors and Affiliations

  1. Department of Mathematics, Government Arts College (Autonomous), (Affiliated to Bharathidasan University, Tiruchirapalli), Kumbakonam, Tamil Nadu, 612 002, India

    G. Jasmine, K. Balaji & R. Aruldoss

Authors
  1. G. Jasmine
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. Balaji
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. R. Aruldoss
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed equally in developing the whole article and granted all the obtained results and revisions. Specifically, G. Jasmine, K. Balaji and R. Aruldoss were involved in conceptualization; G. Jasmine, K. Balaji and R. Aruldoss helped in methodology; G. Jasmine, K. Balaji and R. Aruldoss contributed to software; Validation was done by G. Jasmine, K. Balaji and R. Aruldoss; G. Jasmine, K. Balaji and R. Aruldoss helped in writing—original draft preparation; G. Jasmine, K. Balaji and R. Aruldoss helped in writing—review and editing.

Corresponding author

Correspondence to G. Jasmine.

Ethics declarations

Confict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jasmine, G., Balaji, K. & Aruldoss, R. Numerical Laplace inverse based on operational matrices for fractional differential equations. Int. J. Dynam. Control 12, 75–84 (2024). https://doi.org/10.1007/s40435-023-01333-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-023-01333-z

Keywords

Mathematics Subject Classification (2010)

Search

Navigation