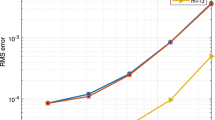
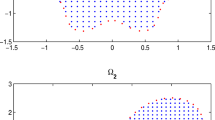
Abstract
Radial basis function-based finite difference (RBF-FD) schemes generalize finite difference methods, providing flexibility in node distribution as well as the shape of the domain. In this paper, we consider a numerical formulation based on RBF-FD for solving a time–space fractional diffusion problem defined using a fractional Laplacian operator. The model problem is simplified into a local problem in space using the Caffarelli–Silvestre extension method. The space derivatives in the resulting problem are then discretized using a local RBF-based finite difference method, while L1 approximation is used for the fractional time derivative. Results obtained using the proposed scheme are then compared with that given in the existing literature.




Similar content being viewed by others
Data availability
Not applicable.
References
Pozrikidis C (2018) The fractional Laplacian. CRC Press, Boca Raton
Zhu T, Harris JM (2014) Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional Laplacians. Geophysics 79:T105–T116
Kwaśnicki M (2017) Ten equivalent definitions of the fractional Laplace operator. Fract Calc Appl Anal 20:7–51
Lischke A, Pang G, Gulian M, Song F, Glusa C, Zheng X, Mao Z, Cai W, Meerschaert MM, Ainsworth M, Karniadakis GE (2019) What is the fractional Laplacian? A comparative review with new results. J Comput Phys 404:109009
Hu Y, Li C, Li H (2017) The finite difference method for Caputo-type parabolic equation with fractional Laplacian: one-dimension case. Chaos Solitons Fractals 102:319–326
Sheng C, Shen J, Tang T, Wang LL, Yuan H (2020) Fast Fourier-like mapped Chebyshev spectral–Galerkin methods for PDEs with integral fractional Laplacian in unbounded domains. SIAM J Numer Anal 58:2435–2464
Bonito A, Borthagaray JP, Nochetto RH, Otárola E, Salgado AJ (2018) Numerical methods for fractional diffusion. Comput Vis Sci 19:19–46
Ainsworth M, Glusa C (2018) Hybrid finite element-spectral method for the fractional Laplacian: approximation theory and efficient solver. SIAM J Sci Comput 40:A2383–A2405
Yuan H (2021) An efficient spectral–Galerkin method for fractional reaction-diffusion equations in unbounded domains. J Comput Phys 428:1–17
Fornberg B, Flyer N (2015) A Primer on Radial Basis Functions with Applications to the Geosciences, Society for Industrial and Applied Mathematics
Zhang Y (2019) An accurate and stable RBF method for solving partial differential equations. Appl Math Lett 97:93–98
Chen W, Ye L, Sun H (2010) Fractional diffusion equations by the Kansa method. Comput Math Appl 59:1614–1620
Piret C, Hanert E (2013) A radial basis functions method for fractional diffusion equations. J Comput Phys 238:71–81
Pang G, Chen W, Fu Z (2015) Space-fractional advection-dispersion equations by the Kansa method. J Comput Phys 293:280–296
Wright GB, Fornberg B (2006) Scattered node compact finite difference-type formulas generated from radial basis functions. J Comput Phys 212:99–123
Caffarelli L, Silvestre L (2007) An extension problem related to the fractional Laplacian. Commun Part Differ Equ 32:1245–1260
Capella A, Dávila J, Dupaigne L, Sire Y (2011) Regularity of radial extremal solutions for some non-local semilinear equations. Commun Part Differ Equ 36:1353–1384
Hu Y, Li C, Li H (2018) The finite difference method for Caputo-type parabolic equation with fractional Laplacian: more than one space dimension. Int J Comput Math 95:1114–1130
Hu Y, Cheng F (2020) The finite element method for fractional diffusion with spectral fractional Laplacian. Math Methods Appl Sci 43:1–17
Kumar P, Erturk V.S, Murillo M, Harley C (2022) Generalized forms of fractional Euler and Runge–Kutta methods using non-uniform grid, Int J Nonlinear Sci Numer Simul
Marasi HR, Derakhshan MH, Joujehi AS, Kumar P (2023) Higher-order fractional linear multi-step methods. Phys Scr 98:024004
Li C, Cai M (2019) Theory and Numerical Approximations of Fractional Integrals and Derivatives, Society for Industrial and Applied Mathematics
Oldham K, Spanier J (1974) The fractional calculus theory and applications of differentiation and integration to arbitrary order, 1st edn. Academic Press, New York, vol 2
Kumar P, Erturk VS, Murillo M, Venkatesan G (2023) A new form of L1-Predictor-Corrector scheme to solve multiple delay-type fractional order systems with the example of a neural network model. Fractals 13:2340043
Acknowledgements
The first author acknowledges CSIR, India, for the financial support through CSIR-JRF/SRF fellowship.
Funding
The research of the corresponding author (Revathy) is supported by the Council of Scientific & Industrial Research (CSIR), India under Grant Number: 09/886(0001)/2019-EMR-I.
Author information
Authors and Affiliations
Contributions
JMR: Literature survey, implementation, manuscript preparation. GC: Ideation, supervision, manuscript editing.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Revathy, J.M., Chandhini, G. Solution of space–time fractional diffusion equation involving fractional Laplacian with a local radial basis function approximation. Int. J. Dynam. Control 12, 237–245 (2024). https://doi.org/10.1007/s40435-023-01237-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40435-023-01237-y