Skip to main content
SpringerLink
Log in

Optimal control of a MEMS gyroscope based on the Koopman theory

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

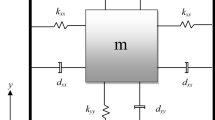
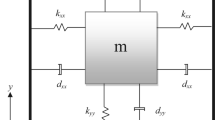
Abstract

Microelectromechanical (MEMS) gyroscopes are small devices used in different industries such as automotive and robotics systems due to their small size and low costs. The MEMS gyroscopes constantly encounter external disturbances, which introduce some mechanical and electromechanical nonlinearity in those systems. In this paper, the Koopman theory is applied to the nonlinear dynamic model of MEMS gyroscope to the linear dynamics model. Dynamic mode decomposition (DMD) is used to obtain eigenfunctions using Koopman’s theory to linearize the system. Then, a linear quadratic regulator (LQR) controller is used to control the MEMS gyroscope. The simulation results verify the performance of the proposed controller in terms of high-tracking performance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Cui J, and Zhao Q (2021) A tactical-grade monolithic horizontal dual-axis mems gyroscope based on off-plane quadrature coupling suppression silicon gratings. In 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS) (pp. 814–817). IEEE.

  2. Wang Z, and Fei J (2021) Double loop neural fractional-order terminal sliding mode control of MEMS Gyroscope. In 2021 Second International Symposium on Instrumentation, Control, Artificial Intelligence, and Robotics (ICA-SYMP) (pp. 1–4). IEEE.

  3. Varghese PM, and Priya PL (2018) Robust control of a dimensionless dual axis MEMS vibratory gyroscope-a sliding mode approach. In 2018 International CET Conference on Control, Communication, and Computing (IC4) (pp. 57–62). IEEE.

  4. Rahmani M (2018) MEMS gyroscope control using a novel compound robust control. ISA Trans 72:37–43

    Article  Google Scholar 

  5. Zhou Y, Fan Q, Liu M, Ren J, Zhou T, Su Y (2021) Design of force-to-rebalanced system with adaptive fuzzy-PID controller for N= 3 MEMS disk gyroscope. IEEE Sens J 21(12):13384–13393

    Article  Google Scholar 

  6. Rahmani M, Komijani H, Ghanbari A, Ettefagh MM (2018) Optimal novel super-twisting PID sliding mode control of a MEMS gyroscope based on multi-objective bat algorithm. Microsyst Technol 24(6):2835–2846

    Article  Google Scholar 

  7. Luo S, Yang G, Li J, Ouakad HM (2022) Dynamic analysis, circuit realization and accelerated adaptive backstepping control of the FO MEMS gyroscope. Chaos, Solitons Fractals 155:111735

    Article  Google Scholar 

  8. Zirkohi MM (2022) Adaptive backstepping control design for MEMS gyroscope based on function approximation techniques with input saturation and output constraints. Comput Electr Eng 97:107547

    Article  Google Scholar 

  9. Zirkohi MM (2022) Adaptive interval type-2 fuzzy recurrent RBFNN control design using ellipsoidal membership functions with application to MEMS gyroscope. ISA Trans 119:25–40

    Article  Google Scholar 

  10. Shi Y, Shao X, Zhang W (2020) Neural observer-based quantized output feedback control for MEMS gyroscopes with guaranteed transient performance. Aerosp Sci Technol 105:106055

    Article  Google Scholar 

  11. Shao X, Shi Y, Zhang W (2021) Input-and-measurement event-triggered output-feedback chattering reduction control for MEMS gyroscopes. IEEE Trans Syst, Man, Cybern: Syst. 25:54

    Google Scholar 

  12. Shao X, Shi Y, Zhang W, Cao H (2020) Neurodynamic approximation-based quantized control with improved transient performances for MEMS gyroscopes: theory and experimental results. IEEE Trans Industr Electron 68(10):9972–9983

    Article  Google Scholar 

  13. Shao X, and Shi Y (2021) Neural-network-based constrained output-feedback control for MEMS gyroscopes considering scarce transmission bandwidth. IEEE Trans Cybern

  14. Shao X, Si H, Zhang W (2021) Fuzzy wavelet neural control with improved prescribed performance for MEMS gyroscope subject to input quantization. Fuzzy Sets Syst 411:136–154

    Article  MathSciNet  MATH  Google Scholar 

  15. Arbabi H (2018) Introduction to Koopman operator theory of dynamical systems. Introduction to Koopman operator theory of dynamical systems.

  16. Abraham I, Murphey TD (2019) Active learning of dynamics for data-driven control using Koopman operators. IEEE Trans Rob 35(5):1071–1083

    Article  Google Scholar 

  17. Korda M, Mezić I (2020) Optimal construction of Koopman eigenfunctions for prediction and control. IEEE Trans Autom Control 65(12):5114–5129

    Article  MathSciNet  MATH  Google Scholar 

  18. Bruder D, Fu X, Gillespie RB, Remy CD, Vasudevan R (2020) Data-driven control of soft robots using koopman operator theory. IEEE Trans Rob 37(3):948–961

    Article  Google Scholar 

  19. Folkestad C, and Burdick JW (2021) Koopman NMPC: Koopman-based learning and nonlinear model predictive control of control-affine systems. In 2021 IEEE International Conference on Robotics and Automation (ICRA) (pp. 7350–7356). IEEE.

  20. Umathe B, Tellez-Castro D, Vaidya U (2022) Reachability analysis using spectrum of Koopman operator. IEEE Control Systems Letters 7:595–600

    Article  MathSciNet  Google Scholar 

  21. Haseli M, Cortés J (2022) Temporal forward-backward consistency, not residual error, measures the prediction accuracy of extended dynamic mode decomposition. IEEE Control Syst Lett 7:649–654

    Article  MathSciNet  Google Scholar 

  22. Guo W, Zhao S, Cao H, Yi B, Song X (2023) Koopman operator-based driver-vehicle dynamic model for shared control systems. Appl Math Model 114:423–446

    Article  MATH  Google Scholar 

  23. Mamakoukas G, Castano ML, Tan X, Murphey TD (2021) Derivative-based koopman operators for real-time control of robotic systems. IEEE Trans Rob 37(6):2173–2192

    Article  Google Scholar 

  24. Son SH, Narasingam A, and Kwon JSI (2021) Integration of offset-free control framework with Koopman Lyapunov-based model predictive control. In 2021 American Control Conference (ACC) (pp. 2818–2823). IEEE.

  25. Goswami D, and Paley DA (2021) Bilinearization, reachability, and optimal control of control-affine nonlinear systems: a Koopman spectral approach. IEEE Trans Autom Control.

  26. Brunton SL, Brunton BW, Proctor JL, Kutz JN (2016) Koopman invariant subspaces and finite linear representations of nonlinear dynamical systems for control. PLoS One 11(2):e0150171

    Article  Google Scholar 

  27. Mamakoukas G, Castano M, Tan X, and Murphey T (2019) Local Koopman operators for data-driven control of robotic systems. In Robot: Sci Syst

  28. Rahmani M, Rahman MH, Nosonovsky M (2020) A new hybrid robust control of MEMS gyroscope. Microsyst Technol 26(3):853–860

    Article  Google Scholar 

  29. Yan W, Hou S, Fang Y, Fei J (2017) Robust adaptive nonsingular terminal sliding mode control of MEMS gyroscope using fuzzy-neural-network compensator. Int J Mach Learn Cybern 8(4):1287–1299

    Article  Google Scholar 

  30. Su Y, Xu P, Han G, Si C, Ning J, Yang F (2020) The characteristics and locking process of nonlinear MEMS gyroscopes. Micromachines 11(2):233

    Article  Google Scholar 

  31. Zhang R, Shao T, Zhao W, Li A, Xu B (2018) Sliding mode control of MEMS gyroscopes using composite learning. Neurocomputing 275:2555–2564

    Article  Google Scholar 

  32. Kaiser E, Kutz JN, Brunton SL (2021) Data-driven discovery of Koopman eigenfunctions for control. Mach Learn: Sci Technol 2(3):035023

    Google Scholar 

  33. Snyder G, and Song Z (2021) Koopman operator theory for nonlinear dynamic modeling using dynamic mode decomposition. arXiv preprint arXiv:2110.08442.

  34. Prasad LB, Tyagi B, Gupta HO (2014) Optimal control of nonlinear inverted pendulum system using PID controller and LQR: performance analysis without and with disturbance input. Int J Autom Comput 11(6):661–670

    Article  Google Scholar 

  35. Anjali BS, Vivek A, Nandagopal JL (2016) Simulation and analysis of integral LQR controller for inner control loop design of a fixed wing micro aerial vehicle (MAV). Procedia Technol 25:76–83

    Article  Google Scholar 

Download references

Funding

This article is based upon work supported by the National Science Foundation (Grant No. 1828010).

Author information

Authors and Affiliations

  1. The Polytechnic School, Ira Fulton School of Engineering, Arizona State University, Mesa, AZ, 85212, USA

    Mehran Rahmani & Sangram Redkar

Authors
  1. Mehran Rahmani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sangram Redkar
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the study conception and design. Material preparation, data collection, and analysis were performed by MR and Dr. SR. The first draft of the manuscript was written by MR and Dr. SR commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Mehran Rahmani.

Ethics declarations

Conflict of interest

There is no conflict of interest.

Ethical Statement

I hereby declare that this manuscript is the result of my independent creation under the reviewer’s comments. Except for the quoted contents, this manuscript does not contain any research achievements that have been published or written by other individuals or groups. Mehran Rahmani and Sangram Redkar are the only authors of this manuscript. The legal responsibility of this statement shall be borne by me.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rahmani, M., Redkar, S. Optimal control of a MEMS gyroscope based on the Koopman theory. Int. J. Dynam. Control 11, 2256–2264 (2023). https://doi.org/10.1007/s40435-022-01110-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-022-01110-4

Keywords

Search

Navigation