Skip to main content
SpringerLink
Log in

A novel fuzzy sliding mode observer for suspension systems

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

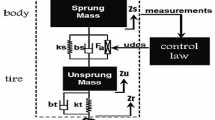
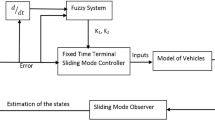
This study presents a novel method to design an observer for nonlinear systems based on fuzzy sliding mode control. In general, there is no standard method for the observer design in nonlinear systems. The proposed observer can be used for a wide range of control systems and its estimates are desirable. In this work, an observer was designed for a nonlinear system as well as a nonlinear quarter vehicle suspension system, the equations of which were derived using Lagrange method, to determine the performance and efficiency. The sliding mode control was used for the nonlinear equations in question. Sliding mode control has long been applied to control systems with modeling uncertainty. This controller is of robust type; however, it has some problems. Fuzzy control is a popular method that can be combined with sliding mode control to solve some of its problems and improve the efficiency of the controller-observer system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  1. Li HX, Gatland HB, Green AW (1997) Fuzzy variable structure control. IEEE Trans Syst Man Cybern 27(2):306–312

    Article  Google Scholar 

  2. Chwee K, Li Y (1994) Design of sophisticated fuzzy logic controllers using genetic algorithms. In: Proceedings of 1994 IEEE 3rd international fuzzy systems conference

  3. Piltan F, Nabaee A, Ebrahimi M, Bazregar M (2013) Design robust fuzzy sliding mode control technique for robot manipulator systems with modeling uncertainties. J Inf Technol Comput Sci 5(8):123–135

    Google Scholar 

  4. Wen S, Chen MZQ, Zeng Z, Yu X (2016) Fuzzy control for uncertain vehicle active suspension systems via dynamic sliding-mode approach. IEEE Trans Syst Man Cybern Syst 47(1):24–32

    Article  Google Scholar 

  5. Taran B, Pirmohammadi A (2019) Designing an optimal fuzzy sliding mode control for a two-link robot. J Braz Soc Mech Sci Eng 42(1):1–12

    Google Scholar 

  6. Dorostian M, Moradmand A (2021) Hierarchical robust model-based predictive control in supply chain management under demand uncertainty and time-delay.In: 2021 7th international conference on control, instrumentation and automation (ICCIA), pp 1–6

  7. Moradmand A, Dorostian M, Shafai B (2020) Energy scheduling for residential distributed energy resources with uncertainties using model-based predictive control. arXiv preprint arXiv:2007.11182

  8. Moradmand, PA, Khaloozadeh H (2017) An experimental study of modeling and self-tuning regulator design for an electro-hydro servo-system. In 2017 5th International Conference on Control, Instrumentation, and Automation (ICCIA), pp 126–131

  9. Habibnejad-Korayem M, Ghobadi N, Fathollahi-Dehkordi S (2021) Designing an optimal control strategy for a mobile manipulator and its application by considering the effect of uncertainties and wheel slipping. Optim Control Appl Methods 42(5):1487–1511

    Article  MathSciNet  MATH  Google Scholar 

  10. Ghadiri H, Mohammadi A, Khodadadi H (2022) Fast terminal sliding mode control based on SDRE observer for two-axis gimbal with external disturbances. J Braz Soc Mech Sci Eng 44(2):1–23

    Article  Google Scholar 

  11. Wang X, Tan C-P, Zhou D (2017) A novel sliding mode observer for state and fault estimation in systems not satisfying matching and minimum phase conditions. Automatica 79:290–295

    Article  MathSciNet  MATH  Google Scholar 

  12. Gholami H, Binazadeh T (2018) Sliding-mode observer design and finite-time control of one-sided Lipschitz nonlinear systems with time-delay. Soft Comput 23(15):6429–6440

    Article  MATH  Google Scholar 

  13. Nguyen V-C, Vo A-N, Kang H-J (2020) A non-singular fast terminal sliding mode control based on third-order sliding mode observer for a class of second-order uncertain nonlinear systems and its application to robot manipulators. IEEE Access 8:78109–78120

    Article  Google Scholar 

  14. Hong K-S et al (1999) A new model and an optimal pole-placement control of the Macpherson suspension system. SAE Trans pp 2452–2461

  15. Wang Z, Dong M, Qin Y, Du Y, Zhao F, Gu L (2016) Suspension system state estimation using adaptive Kalman Filtering Based on road classification. Veh Syst Dyn 55(3):371–398

    Article  Google Scholar 

  16. He J-H (2019) The simpler, the better: analytical methods for nonlinear oscillators and fractional oscillators. J Low Freq Noise Vib Active Control 38(3–4):1252–1260

    Article  Google Scholar 

  17. Liu H-Y, Li Z-M, Yao S-W, Yao Y-J, Liu J (2020) A variational principle for the photocatalytic NOx abatement. Therm Sci 24(4):2515–2518

    Article  Google Scholar 

  18. Yao S-W (2021) Variational principle for nonlinear fractional wave equation in a fractal space. Therm Sci pp 18–18

  19. He J-H, Amer T-S, Elnaggar S, Galal A-A (2021) Periodic property and instability of a rotating pendulum system. Axioms 10(3):191

    Article  Google Scholar 

  20. He C-H, Tian D, Moatimid G-M, Salman H-F, Zekry M-H (2021) Hybrid rayleigh–van der pol–duffing oscillator: stability analysis and controller. J Low Freq Noise Vib Active Control

  21. Tian D, Ain Q-T, Anjum N, He C-H, Cheng A-B (2021) Fractal N/MEMS: from pull-in instability to pull-in stability. Fractals 29(2):2150030

    Article  MATH  Google Scholar 

  22. Slotine JJE, Li W (1991) Applied nonlinear control, vol 199, no 1, Prentice Hall, Englewood Cliffs

  23. Sulaiman M, Patakor F-A, Ibrahim Z (2014) New methodology for chattering suppression of sliding mode control for three-phase induction motor drives. WSEAS Trans Syst Control pp 1–9

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Tarbiat Modares University, Jalal AleAhmad Highway, Nasr Bridge, P.O.Box: 14115-111, Tehran, Iran

    Babak Taran & Amin Ramezani

  2. Department of Electrical and Computer Engineering, Tarbiat Modares University, Jalal AleAhmad Highway, Nasr Bridge, P.O.Box: 14115-111, Tehran, Iran

    Babak Taran & Amin Ramezani

Authors
  1. Babak Taran
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Amin Ramezani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Babak Taran.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Funding

The authors have not received any funding from any organization.

Availability of data and material

All data and material are available.

Code availability

The codes for this article are available.

Authors’ contributions

Babak Taran: Methodology, Software, Writing; Amin Ramezani: Methodology, Resources, review & editing

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Taran, B., Ramezani, A. A novel fuzzy sliding mode observer for suspension systems. Int. J. Dynam. Control 10, 1889–1902 (2022). https://doi.org/10.1007/s40435-022-00957-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-022-00957-x

Keywords

Search

Navigation