Skip to main content
SpringerLink
Log in

Providing robust-adaptive fractional-order sliding mode control in hybrid adaptive cruise control systems in the presence of model uncertainties and external disturbances

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

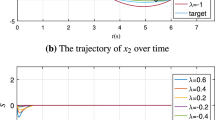
This paper deals with the stabilizing of hybrid adaptive cruise control (ACC) systems in the presence of external disturbances and model uncertainties. Considering that upper bound of model uncertainties and external disturbances is a nonlinear function of ACC system states with unknown coefficients, a new robust-adaptive fractional-order sliding mode controller (RAFOSMC) is developed. The unknown coefficients of the functional upper bound of perturbations are obtained via some stable adaptive rules. Stability proof of the proposed RAFOSMC is presented based on Lyapunov theorem. It is also analytically shown that the proposed FOSMC has better performance than ordinary integer-order sliding mode controllers (IOSMC). Using FOSMC benefits a significant reduction in chattering and also faster convergence to the vehicle's safe distance in the vehicle's initial movement. Finite-time convergence of system states to the fractional sliding surface is then obtained, and a new approximation of sign function for more chattering elimination is also proposed in this paper. Simulation results and presented comparisons at the end of this paper show the effectiveness of the proposed methodologies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Madhusudhanan AK (2019) A method to improve an electric vehicle’s range: efficient cruise control. Eur J Control 48:83–96

    Article  MathSciNet  MATH  Google Scholar 

  2. Ganesan M, Ezhilarasi D, Benn J (2017) Second-order sliding mode controller with model reference adaptation for automatic train operation. Int J Veh Mech Mobil. https://doi.org/10.1080/00423114.2017.1330482

    Article  Google Scholar 

  3. Mizoshiri T, Mori Y (2017) Application of adaptive sliding mode control with an ellipsoidal sliding surface for vehicle distance control. SICE J Control MeasSyst Integr 10(1):25–31

    Article  Google Scholar 

  4. Trotta A, Cirillo A, Giorelli M (2019) A feedback linearization based approach for fully autonomous adaptive cruise control. In: 2019 18th European control conference (ECC) Napoli, Italy, 25–28 June 2019

  5. Lin YC, Hsu HC, Chen WJ (2016) Dynamic programming for model predictive control of adaptive cruise control systems. In: 2015 IEEE international conference on vehicular electronics and safety (ICVES), 2016, pp 202–207

  6. Luo L (2019) Adaptive cruise control design with consideration of humans’ driving psychology. In: Proceeding of the 11th world congress on intelligent control and automation, 2019, 973–2978

  7. Luu DL, Lupu C, Cristian I, Doan VK (2021) Speed control and spacing control for autonomous mobile robot platform equipped with infrared sensors. In: 2021 16th international conference on engineering of modern electric systems (EMES), 2021, pp 1–4

  8. Alonso L, Pérez-Oria J (2014) Genetic optimization of fuzzy adaptive cruise control for urban traffic. In: Matía F, Marichal GN, Jiménez E (eds) Fuzzy modeling and control: theory and applications. Springer, pp 255–271

    Google Scholar 

  9. Wang Z, Gao Y, Fang C, Sun Y, Si P (2019) Optimal control design for connected cruise control with edge computing, caching, and control. In: IEEE INFOCOM 2019: IEEE conference on computer communications workshops (INFOCOM WKSHPS), 2019, pp 1–6

  10. Moser D, Schmied R, Waschl H, del Re L (2018) Flexible spacing adaptive cruise control using stochastic model predictive control. IEEE Trans Control Syst Technol 26:114–127

    Article  Google Scholar 

  11. Wang X, Zhu L, Wang H, Tang T, Li K (2021) Robust distributed cruise control of multiple high-speed trains based on disturbance observer. IEEE Trans Intell Transp Syst 22(1):267–279

    Article  Google Scholar 

  12. Hidayatullah MR, Juang J-C (2021) Adaptive cruise control with gain scheduling technique under varying vehicle mass. IEEE Access 9:144241–144256

    Article  Google Scholar 

  13. Utkin VI, Guldner J, Shi J (2009) Sliding mode control in electro-mechanical systems, 2nd edn. CRC Press, Boca Raton

    Google Scholar 

  14. Sun Zh, Zhong G, Lu Y, Zhang W (2018) Leader-follower formation control of underactuated surface vehicles based on sliding mode control and parameter estimation. ISA Trans 72:15–24

    Article  Google Scholar 

  15. Shahravi M, Azimi M (2016) A hybrid scheme of synthesized sliding mode/strain rate feedback control design for flexible spacecraft attitude maneuver using time scale decomposition. Int J Struct Stab Dyn 16(2):1450101

    Article  MathSciNet  MATH  Google Scholar 

  16. Azimi M (2020) Stabilization of a large flexible spacecraft using robust adaptive sliding hypersurface and finite element approach. Int J Dyn Control 8(2):644–655

    Article  MathSciNet  Google Scholar 

  17. Azimi M, Moradi S (2021) “Robust optimal solution for a smart rigid–flexible system control during multimode operational mission via actuators in combination. Multibody Syst Dyn 52(3):313–337

    Article  MathSciNet  MATH  Google Scholar 

  18. Ferrara A, Pisu P (2004) Minimum sensor second-order sliding mode longitudinal control of passenger vehicles. IEEE Trans Intell Transp Syst 5(1):20–32

    Article  Google Scholar 

  19. Li Z, Song A (2009) Sliding mode control based on tracking differentiator for intelligent vehicle headway distance control. In: Proceedings of the IEEE international conference on intelligent computing and intelligent systems (ICIS) Shanghai, Nov 2009, pp 489–493

  20. Polyakov A, Fridman L (2014) Stability notions and Lyapunov functions for sliding mode control systems. J Frankl Inst 351(4):1831–1865

    Article  MathSciNet  MATH  Google Scholar 

  21. Gonzalez T, Moreno JA, Fridman L (2012) Variable gain super-twisting sliding mode control. IEEE Trans Autom Control 57(8):2100–2105

    Article  MathSciNet  MATH  Google Scholar 

  22. Soorki MN, Tavazoei MS (2018) Adaptive robust control of fractional-order systems in the presence of model uncertainties and external disturbances. IET Control Theory Appl 12(7):961–969

    Article  MathSciNet  Google Scholar 

  23. Wang HP, Mostafa Ghazally IY, Tian Y (2018) Model-free fractional-order sliding mode control for an active vehicle suspension system. Adv Eng Softw 115:452–461

    Article  Google Scholar 

  24. Yin C, Chen YQ, Zhong SM (2014) Fractional-order sliding mode based extremum seeking control of a class of nonlinear systems. Automatica 50(12):3173–3181

    Article  MathSciNet  MATH  Google Scholar 

  25. Yin C, Huang X, Chen Y, Dadras S, Zhong SM, Cheng Y (2017) Fractional-order exponential switching technique to enhance sliding mode control. Appl Math Model 44:705–726

    Article  MathSciNet  MATH  Google Scholar 

  26. Corona D, Schutter BD (2007) Comparison of a linear and a hybrid adaptive cruise controller for a SMART. In: Proceedings of the 46th IEEE conference on decision and control New Orleans. LA, USA, 12–14 Dec 2007

  27. Podlubny I (2018) Fractional-order-based ACC/CACC algorithm for improving string stability. Preprint submitted to transportation research part C: emerging technologies, 26 July 2018

  28. Naderi Soorki M, Tavazoei MS (2016) Asymptotic swarm stability of fractionalorder swarm systems in the presence of time-delays. Int J Control 90(6):1182–1191

    Article  MATH  Google Scholar 

  29. Yin C, Xue J, Cheng Y, Zhang B, Zhou J (2018) Fractional-order non-singular fast terminal sliding mode control technique for the 6-DOF robotic manipulator. In: Proceedings of the 37th Chinese control conference, Wuhan, China, 25–27 July 2018

  30. Soorki MN, Tavazoei MS (2013) Fractional-order linear time-invariant swarm systems: asymptotic swarm stability and time response analysis. Cent Eur J Phys 11(6):845–854

    Google Scholar 

  31. Zhang BT, Pi YG, Luo Y (2012) Fractional-order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor. ISA Trans 51(5):649–656

    Article  Google Scholar 

  32. Ganji B, Kouzani AZ, Khoo SY, Nasir M (2014) A sliding-mode-control-based adaptive cruise controller. In: 11th IEEE international conference on control & automation (ICCA), Taichung, Taiwan, 18–20sss June 2014

Download references

Funding

There is not funding to report for this submission.

Author information

Authors and Affiliations

  1. Faculty of Electrical Engineering, Shahrood University of Technology, Shahrood, Iran

    Sajjad Sheykhi & Hossein Gholizade-Narm

Authors
  1. Sajjad Sheykhi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hossein Gholizade-Narm
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

S. Sheykhi: Conceptualization, Methodology, Software, Writing-Original draft, H. Gholizade: Formal analysis, Investigation, Visualization, Supervision, Project administration.

Corresponding author

Correspondence to Sajjad Sheykhi.

Ethics declarations

Conflict of interest

The authors whose names are listed immediately aboved certify that they have NO affiliations with or involvement in any organization or entity with any financial interest (such as honoraria; educational grants; participation in speakers’ bureaus; membership, employment, consultancies, stock ownership, or other equity interest; and expert testimony or patent-licensing arrangements), or non-financial interest (such as personal or professional relationships, affiliations, knowledge or beliefs) in the subject matter or materials discussed in this manuscript.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sheykhi, S., Gholizade-Narm, H. Providing robust-adaptive fractional-order sliding mode control in hybrid adaptive cruise control systems in the presence of model uncertainties and external disturbances. Int. J. Dynam. Control 10, 1955–1967 (2022). https://doi.org/10.1007/s40435-022-00936-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-022-00936-2

Keywords

Search

Navigation