Skip to main content
SpringerLink
Log in

Active vibration control of typical piping system of a nuclear power plant based on fractional PI controller

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

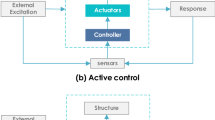
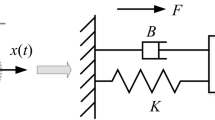
An active control method based on fractional PI is studied to reduce the vibration of the typical pipeline system of a nuclear power plant. The mathematical model of the typical piping system of the nuclear power plant is established, and the fractional-order PI output feedback controller and the fractional-order PI state feedback controller are designed to realize the active control of vibration. In view of the large number of parameters of high-dimensional fractional PI controllers and the difficulty of tuning, the sparrow search algorithm (SSA) is adopted, and the quadratic function of the system is used as the objective function to realize the tuning of the controller parameters. The fractional-order PI controller optimized based on the SSA and the integer-order PI controller are compared for experiments. The results show that the fractional-order PI controller has a better suppression effect on the vibration of the typical piping system of nuclear power plants.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Errico F, Petrone G, De Rosa S, Franco F, Ichchou M (2021) On the concept of embedded resonators for passive vibration control of tyres. Proc Inst Mech Eng Part C J Mech Eng Sci 235(14):2587–2593. https://doi.org/10.1177/0954406221999427

    Article  Google Scholar 

  2. Sun X, Kong F, Li S (2015) Seismic reliability of passive controlled MDOF structures equipped with viscous fluid dampers based on local stationary method. J Vib Eng 28(03):394–403. https://doi.org/10.16385/j.cnki.issn.1004-4523.2015.03.008

    Article  Google Scholar 

  3. Elizabeth N, Kuinian L (2018) Experimental investigation on a passive auto-tuning mass damper for vibration control. Int J Dyn Control 6(3):1047–1062. https://doi.org/10.1007/s40435-017-0381-z

    Article  Google Scholar 

  4. Alan G, Antonio A, Eisenhawer D et al (2021) Active vibration control in a two degrees of freedom structure using piezoelectric transducers associated with negative capacitance shunt circuits. Int J Dyn Control 9(1):71–84. https://doi.org/10.1007/S40435-020-00652-9

    Article  Google Scholar 

  5. Zhang C, Wang H (2021) Structural pendulum vibration control methods based on Active Rotary Inertia DriverARIDsystem Theoretical modeling and experimental verification. J Vib Eng 34(01):20–28. https://doi.org/10.16385/j.cnki.issn.1004-4523.2021.01.003

    Article  Google Scholar 

  6. Desai R, Guha A, Seshu P (2021) Modelling and simulation of active and passive seat suspensions for vibration attenuation of vehicle occupants. Int J Dyn Control 9(4):1423–1443. https://doi.org/10.1007/S40435-021-00788-2

    Article  Google Scholar 

  7. Jin Q, Wen J, Narayanan S (2021) Experimental study and mitigation of pressure drop oscillation using active control. J Electron Packag 143(4):041102. https://doi.org/10.1115/1.4051942

    Article  Google Scholar 

  8. Jiao Z, Chen P, Hua Q, Wang S (2002) Theoretical study on vibration active control of power supply and pipeline systems. J Beijing Univ Aeronaut Astronaut 2002(04):465–469. https://doi.org/10.13700/j.bh.1001-5965.2002.04.026

    Article  Google Scholar 

  9. Liu H, Yang Z, Niu W, Li K, Wang W (2021) NAF-FxLMS controller for vertical tail buffeting active control. Vib Shock 40(06):140–146. https://doi.org/10.13465/j.cnki.jvs.2021.06.019

    Article  Google Scholar 

  10. Aggogeri F, Merlo A, Pellegrini N (2021) Active vibration control development in ultra-precision machining. J Vib Control 27(7–8):790–801. https://doi.org/10.1177/1077546320933477

    Article  Google Scholar 

  11. Mohamed A, Mahmoud M, Swief R, Said L, Radwan A (2021) Optimal fractional-order PI with DC–DC converter and PV system. Ain Shams Eng J 12(2):1895–1906. https://doi.org/10.1016/J.ASEJ.2021.01.005

    Article  Google Scholar 

  12. Mande D, Blondin M, Trovao J (2020) Optimisation of fractional-order PI controller for bidirectional quasi-Z-source inverter used for electric traction system. IET Electr Syst Transport 10(4):376–384. https://doi.org/10.1049/IET-EST.2020.0005

    Article  Google Scholar 

  13. Jiang J, Jiang J, Chen S, Yang X, Cai Z (2020) Application of fractional order PI control in single-phase active power factor corrector. J Phys Conf Ser 1585(1):2028. https://doi.org/10.1088/1742-6596/1585/1/012028

    Article  Google Scholar 

  14. Hao C, Wei X, Xiyang C, Jingang H, Nadia A, Zhibin Z, Tianhao T, Mohamed B (2020) Fractional-order PI control of DFIG-based tidal stream turbine. J Mar Sci Eng 8(5):309. https://doi.org/10.3390/jmse8050309

    Article  Google Scholar 

  15. Abdullah B, Kaan C, Kamil O, Derdiyok A (2017) Trajectory tracking control of a four rotor unmanned aerial vehicle based on continuous sliding mode controller. Elektronika ir Elektrotechnika 23(3):12–19. https://doi.org/10.5755/j01.eie.23.3.18325

    Article  Google Scholar 

  16. Alessandro P, Milan R, Zoran J, Elio U (2021) Nonlinear fractional PI control of a class of fractional-order systems. IFAC-PapersOnLine 45(3):637–642. https://doi.org/10.3182/20120328-3-IT-3014.00108

    Article  Google Scholar 

  17. Feliu B, Rodriguez L, Perez R, Tercero D, Saez A, Marinoso J, Garcia P (2007) Fractional PI control of an irrigation main canal. IFAC-PapersOnLine 40(1):280–285. https://doi.org/10.3182/20070213-3-CU-2913.00048

    Article  Google Scholar 

  18. Xue J, Shen B (2020) A novel swarm intelligence optimization approach: sparrow search algorithm. Syst Sci Control Eng 8(1):22–34. https://doi.org/10.1080/21642583.2019.1708830

    Article  Google Scholar 

  19. Pan F, Liu L, Xue D (2017) Optimal PID controller design with Kalman filter for Qball-X4 quad-rotor unmanned aerial vehicle. Trans Inst Meas Control 39(12):1785–1797. https://doi.org/10.1177/0142331216656753

  20. Wu S (2021) A nonhomogeneous mean-field linear-quadratic optimal control problem and application. Acta Math Appl Sin 37(4):807–819. https://doi.org/10.1007/S10255-021-1045-5

    Article  MathSciNet  MATH  Google Scholar 

  21. Tang C, Li X, Huang T (2020) Solvability for indefinite mean-field stochastic linear quadratic optimal control with random jumps and its applications. Optim Control Appl Methods 41(3):2320–2348. https://doi.org/10.1002/oca.2659

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This study was financially supported by the Science and Technology on Reactor System Design Technology Laboratory (HT-KFKT-02-2019010).Basic Scientific Research Project of Higher Education Institutions of Education Department of Liaoning Province (General Project)(No. LJKZ0245)

Author information

Authors and Affiliations

  1. School of Automation and Electrical Engineering, Shenyang Ligong University, Shenyang, 110159, China

    Yanzhu Zhang & Xiaomeng Zhang

  2. Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu, 610000, China

    Fu-Rui Xiong

  3. School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an, 710072, China

    Lu Liu

  4. School of Mathematics and Statistics, Northwestern Polytechnical University, Xi’an, 710072, China

    Shuo Zhang

Authors
  1. Yanzhu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaomeng Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fu-Rui Xiong
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lu Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Shuo Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Ethics declarations

Conflict of interest

I declare that there is no conflict of interest in the publication of this article, and that there is no conflict of interest with any other author or institution for the publication of this article.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y., Zhang, X., Xiong, FR. et al. Active vibration control of typical piping system of a nuclear power plant based on fractional PI controller. Int. J. Dynam. Control 10, 2111–2123 (2022). https://doi.org/10.1007/s40435-022-00926-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-022-00926-4

Keywords

Search

Navigation