Skip to main content
SpringerLink
Log in

Stabilizing unstable periodic orbits of dynamical systems using delayed feedback control with periodic gain

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

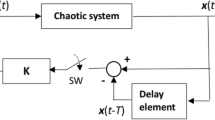
Two algorithms of unstable periodic orbits stabilization based on delayed feedback control and periodic gain are discussed. The efficiency of these algorithms for stabilization of unstable periodic orbits of the Lorenz and Rossler systems and visualization of stabilized periodic orbits are demonstrated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Ott E, Grebogi C, Yorke J (1990) Controlling chaos. Phys Rev Lett 64:11961199

    MathSciNet  MATH  Google Scholar 

  2. Pyragas K (1992) Continuous control of chaos by self-controlling feedback. Phys Lett A 170:421–428

    Article  Google Scholar 

  3. Namajunas A, Pyragas K, Tamaeviius A (1995) Stabilization of an unstable steady state in a Mackey–Glass system. Phys Lett A 204:255–262

    Article  Google Scholar 

  4. Pyragas V, Pyragas K (2006) Delayed feedback control of the Lorenz system: an analytical treatment at a subcritical hopf bifurcation. Phys Rev E 73:1–10

    Article  MathSciNet  MATH  Google Scholar 

  5. Tamaeviius A, Mykolaitis G, Pyragas V, Pyragas K (2007) Delayed feedback control of periodic orbits without torsion in nonautonomous systems: theory and experiment. Phys Rev E 76:1–6

    Google Scholar 

  6. Pyragas K (1995) Control of chaos via extended delay feedback. Phys Rev A 206:323–330

    MathSciNet  MATH  Google Scholar 

  7. Pyragas K (2006) Delayed feedback control of chaos. Philos Trans R Soc A 369:20392334

    MathSciNet  MATH  Google Scholar 

  8. Pyragas K (2012) A twenty-year review of time-delay feedback control and recent developments. In: International symposium on nonlinear theory and its applications, Spain, pp 683–686

  9. Pyragas K (2016) Act-and-wait time-delayed feedback control of nonautonomous systems. Phys Rev E 94(012):201

    Google Scholar 

  10. Tian Y, Zhu J, Chen G (2005) A survey on delayed feedback control of chaos. J Control Theory Appl 4:311319

    MathSciNet  Google Scholar 

  11. Hovel P, Scholl E (2005) Control of unstable steady states by time-delayed feedback methods. Phys Rev E 72:46203

    Article  Google Scholar 

  12. Scholl E, Shuster H (2008) Handbook of chaos control, 2nd edn. Wiley-VCH, Weinheim

    Google Scholar 

  13. Ahlborn A, Parlitz U (2005) Controlling dynamical systems using multiplie delay feedback control. Phys Rev E 72:16206

    Article  MathSciNet  Google Scholar 

  14. Yanchuk S, Wolfrum M, Hovel P, Scholl E (2006) Control of unstable steady states by long delay feedback. Phys Rev E 74(026):201

    MathSciNet  Google Scholar 

  15. Lorenz EN (1963) Deterministic nonperiodic flow. J Atmos Sci 20:130141

    Google Scholar 

  16. Leonov GA (2014) Pyragas stabilizability via delayed feedback with periodic control gain. Syst Control Lett 69:34–37

    Article  MathSciNet  MATH  Google Scholar 

  17. Leonov GA (2015) Pyragas stabilizability via delayed feedback with periodic control gain. Dokl Akad Nauk 463:278–279 (in Russian)

  18. Brockett R (1999), A stabilization problem. In: Open problems in mathematical systems and control theory. Springer, London, pp 75–78

  19. Leonov GA (2002) Brocketts problem in the theory of stability of linear differential equations. St Petersburg Math J 13:134155

    MathSciNet  Google Scholar 

  20. Leonov GA (2001) Linear nonstationary stabilization algorithms and brockett problem. J Appl Math Mech 65:777783

    Google Scholar 

  21. Leonov GA (2002) Brockett problem in the theory of stability of nonstationary stabilization of linear differential equations. Am Math Soc Trans 205:163173

    Google Scholar 

  22. Leonov GA, Shumafov MM (2011) Stabilization of linear systems. Cambridge Scientific, Cambridge

    MATH  Google Scholar 

  23. Leonov GA, Shumafov MM (2011) Vibrational stabilization and the Brockett problem. Differ Equ 47:18531915

    Article  MathSciNet  MATH  Google Scholar 

  24. Leonov GA (2002) Brocketts problem for linear discrete control systems. Autom Telemech 5:9296

    Google Scholar 

  25. Zhou B, Li Z-Y, Zheng WX, Duan G-R (2012) Stabilization of some linear systems with both state and input delays. Syst Control Lett 61:989998

    MathSciNet  Google Scholar 

  26. Lozi R, Pchelintsev AN (2015) A new reliable numerical method for computing chaotic solutions of dynamical systems: the Chen attractor case. Int J Bifurc Chaos 25(1550):187

    MathSciNet  MATH  Google Scholar 

  27. Pilyugin SY (1999) Shadowing in dynamical systems. Springer, Berlin

    MATH  Google Scholar 

  28. Tucker W (2008) Rigorous study of short periodic orbits for the Lorenz system. In: IEEE international symposium on circuits and systems, pp 764–767

  29. Demidovich BP (1969) Lectures on mathematical theory of stability. Nauka, Moscow (in Russian)

    Google Scholar 

  30. Andrianova LY (1995) Introduction to linear systems of differential equations. Translations of mathematical monographs, vol 146. American Mathematical Society, Providence

    Book  Google Scholar 

  31. Leonov GA, Kuznetsov NV (2007) Time-varying linearization and the Perron effects. Int J Bifurc Chaos 17:10791107

    Article  MathSciNet  MATH  Google Scholar 

  32. Kuznetsov NV, Leonov GA, Shumafov MM (2015) A short survey on Pyragas time-delay feedback stabilization and odd number limitation. IFAC-PapersOnLine 48:706709

    Google Scholar 

  33. Nakajima H, Ueda Y (1998) Limitation of generalized delayed feedback control. Phys D 111:143150

    Article  MathSciNet  MATH  Google Scholar 

  34. Nakajima H (1997) On analytical properties of delayed feedback control of chaos. Phys Lett A 232:207–210

    Article  MathSciNet  MATH  Google Scholar 

  35. Just W, Fiedler B, Georgi M, Flunkert V, Hovel P, Scholl E (2007) Beyond the odd number limitation: a bifurcation analysis of time-delayed feedback control. Phys Rev E. doi:10.1103/hysRevE.76.026210

  36. Hooton EW, Amann A (2012) An analytical limitation for time-delayed feedback control in autonomous systems. Phys Rev Lett 109(154):101

    Google Scholar 

  37. Sparrow C (1982) The Lorenz equations: bifurcations, chaos, and strange attractors. Springer, New York

    Book  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the Russian Scientific Foundation project (14-21-00041, s.3), NSch (8580.2016.1, s.1), RFBR (15-51-45062, s.2) and the Saint-Petersburg State University.

Author information

Authors and Affiliations

  1. Faculty of Mathematics and Mechanics, Saint-Petersburg State University, Saint-Petersburg, Russia

    Gennady A. Leonov & Alexander V. Moskvin

Authors
  1. Gennady A. Leonov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alexander V. Moskvin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alexander V. Moskvin.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Leonov, G.A., Moskvin, A.V. Stabilizing unstable periodic orbits of dynamical systems using delayed feedback control with periodic gain. Int. J. Dynam. Control 6, 601–608 (2018). https://doi.org/10.1007/s40435-017-0316-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-017-0316-8

Keywords

Search

Navigation