Skip to main content
SpringerLink
Log in

Dynamical analysis, linear feedback control and synchronization of a generalized Lotka-Volterra system

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

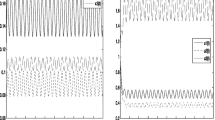
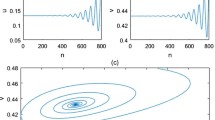
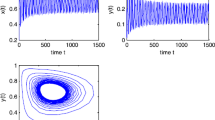
In this paper, a generalized Lotka-Volterra (GLV) system, which is modeled by a set of equations that represents the dynamical behaviors of two-predator and one prey species, is analysed. The boundedness, existence and uniqueness of the solutions of the generalized Lotka-Volterra system are studied. Continuous dependence on initial conditions in the model is also studied to determine the parameter values’ range of the model and time T where the system does not exhibit chaotic behaviors. In addition, extinction scenarios of solutions of the model are discussed. The necessary and sufficient conditions for the asymptotic stability of the equilibrium points of the GLV system are derived. It is also shown that the GLV system undergoes a saddle-node bifurcation and generalized Hopf (Bautin) bifurcation around one of its equilibrium points. The coexisting periodic solutions and chaotic attractors in the system are numerically investigated by phase diagrams and Lyapunov exponent spectrum. Linear feedback control technique is utilized to control the GLV model to its equilibrium points. Moreover, the Lyapunov direct method is used to synchronize two identical chaotic GLV models via linear feedback control technique.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Lorenz EN (1963) Deterministic nonperiodic flow. J Atmos Sci 20(2):130–141

    Article  Google Scholar 

  2. Rössler OE (1976) An equation for continuous chaos. Phys Lett A 57:397–398

    Article  MATH  Google Scholar 

  3. Fu SH, Lu QS (2014) Set stability of controlled Chua’s circuit under a non-smooth controller with the absolute value. Int J Control Autom Syst 12(3):507–517

    Article  Google Scholar 

  4. Chen G, Ueta T (1999) Yet another chaotic attractor. Int J Bifurc Chaos 09(07):1465–1466

    Article  MathSciNet  MATH  Google Scholar 

  5. Matouk AE (2008) Dynamical analysis, feedback control and synchronization of Liu dynamical system. Nonlinear Anal Theory Methods Appl 69(10):3213–3224

    Article  MathSciNet  MATH  Google Scholar 

  6. Matouk AE, Agiza HN (2008) Bifurcations, chaos and synchronization in ADVP circuit with parallel resistor. J Math Anal Appl 341(1):259–269

    Article  MathSciNet  MATH  Google Scholar 

  7. Zhou W, Pan L, Li Z, Halang WA (2009) Non-linear feedback control of a novel chaotic system. Int J Control Autom Syst 7(6):939–944

    Article  Google Scholar 

  8. Pan L, Zhou W, Fang J (2010) Dynamics analysis of a new simple chaotic attractor. Int J Control Autom Syst 8(2):468–472

    Article  Google Scholar 

  9. Mahmoud GM, Bountis T (2004) The dynamics of systems of complex nonlinear oscillators: a review. Int J Bifurc Chaos 14(11):3821–3846

    Article  MathSciNet  MATH  Google Scholar 

  10. Mahmoud GM, Aly SA, AL-Kashif MA (2008) Dynamical properties and chaos synchronization of a new chaotic complex nonlinear system, Nonlinear Dyn 51(1):171–181

    MathSciNet  MATH  Google Scholar 

  11. El-Sayed AMA, Nour HM, Elsaid A, Matouk AE, Elsonbaty A (2014) Circuit realization, bifurcations, chaos and hyperchaos in a new 4D system. Appl Math Comput 239:333–345

    MathSciNet  MATH  Google Scholar 

  12. Lotka AJ (1925) Elements of physical biology. Williams and Wilkins, Baltimore

    MATH  Google Scholar 

  13. Freedman HI, Waltman P (1977) Mathematical analysis of some three-species food-chain models. Math Biosci 33(3–4):257–276

    Article  MathSciNet  MATH  Google Scholar 

  14. Freedman HI (1980) Deterministic mathematical models in population ecology. Marcle Dekker, New York

    MATH  Google Scholar 

  15. Murray JD (1993) Mathematical biology. Springer, New York

    Book  MATH  Google Scholar 

  16. Kuznetsov Y, Rinaldi S (1996) Remarks on food chain dynamics. Math Biosci 134(1):1–33

    Article  MathSciNet  MATH  Google Scholar 

  17. Castillo-Chavez C, Feng Z (1998) Global stability of an age-structure model for TB and its applications to optimal vaccination strategies. Math Biosci 151:135–154

    Article  MATH  Google Scholar 

  18. Kot M (2001) Elements of mathematical ecology. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  19. Castillo-Chavez C, Song B (2004) Dynamical models of tuberculosis and their applications. Math Biosci Eng 1(2):361–404

    Article  MathSciNet  MATH  Google Scholar 

  20. Freedman HI, Waltman P (1984) Persistence in a model of three interacting predator-prey populations. Math Biosci 68:213–231

    Article  MathSciNet  MATH  Google Scholar 

  21. Erbe LH, Freedman HI, Rao VSH (1986) Three-species food-chain models with mutual interference and time delays. Math Biosci 80(1):57–80

    Article  MathSciNet  MATH  Google Scholar 

  22. Gómez JM, Zamora R (1994) Top-down effects in a tritrophic system: parasitoids enhance plant fitness. Ecology 75(4):1023–1030

    Article  Google Scholar 

  23. Xiao Y, Chen L (2001) Modeling and analysis of a predator-prey model with disease in the prey. Math Biosci 171(1):59–82

    Article  MathSciNet  MATH  Google Scholar 

  24. Ruan S, Xiao D (2001) Global analysis in a predator-prey system with nonmonotonic functional response. SIAM J Appl Math 61(4):1445–1472

    Article  MathSciNet  MATH  Google Scholar 

  25. Venturino E (2002) Epidemics in predator-prey models: disease in the predators. Math Med Biol 19(3):185–205

    Article  MATH  Google Scholar 

  26. Tewa JJ, Djeumen VY, Bowong S (2013) Predator-Prey model with Holling response function of type II and SIS infectious disease. Appl Math Model 37:4825–4841

    Article  MathSciNet  Google Scholar 

  27. Sharma S, Samanta GP (2015) Analysis of a two prey one predator system with disease in the first prey population. Int J Dyn Control 3(3):210–224

    Article  MathSciNet  Google Scholar 

  28. Gurubilli KK, Srinivasu PDN, Banerjee M (2016) Global dynamics of a prey-predator model with Allee effect and additional food for the predators. Int J Dyn Control. doi:10.1007/s40435-016-0234-1

    Google Scholar 

  29. Shehata AM, Elaiw AM, Elnahary EK, Abul-Ez M (2016) Stability analysis of humoral immunity HIV infection models with RTI and discrete delays. Int J Dyn Control. doi:10.1007/s40435-016-0235-0

    Google Scholar 

  30. Hastings A, Powell T (1991) Chaos in a three-species food chain. Ecology 72(3):896–903

    Article  Google Scholar 

  31. Holling CS (1965) The functional response of predators to prey density and its role in mimicry and population regulation. Mem Entomol Soc Can 45:3–60

    Google Scholar 

  32. Pielou EC (1977) Mathematical ecology. Wiley, New York

    MATH  Google Scholar 

  33. Upadhyay RK, Rai V (1997) Why chaos is rarely observed in natural populations. Chaos Solitons Fract 8(12):1933–1939

    Article  Google Scholar 

  34. Zimmer C (1999) Life after chaos. Science 284(5411):83–86

    Article  Google Scholar 

  35. Cushing JM, Henson SM, Desharnais RA, Dennis B, Costantino RF, King A (2001) A chaotic attractor in ecology: theory and experimental data. Chaos Solitons Fract 12:219–234

    Article  MathSciNet  MATH  Google Scholar 

  36. Samardzija N, Greller LD (1988) Explosive route to chaos through a fractal torus in a generalized Lotka-Volterra model. Bull Math Biol 50(5):465–491

    Article  MathSciNet  MATH  Google Scholar 

  37. Hsü ID, Kazarinoff ND (1976) An applicable Hopf bifurcation formula and instability of small periodic solutions of the Field-Noyes model. J Math Anal Appl 55:61–89

    Article  MathSciNet  MATH  Google Scholar 

  38. Guckenheimer J, Holmes P (1983) Nonlinear oscillations, dynamical systems, and bifurcations of vector fields. Springer, New York

    Book  MATH  Google Scholar 

  39. Kuznetsov YA (1998) Elements of applied bifurcation theory. Springer, New York

    MATH  Google Scholar 

  40. Kuznetsov YA (1999) Numerical normalization techniques for all codim 2 bifurcations of equilibria in ODE’s. SIAM J Numer Anal 36(4):1104–1124

    Article  MathSciNet  MATH  Google Scholar 

  41. Buica A, Llibre J (2004) Averaging methods for finding periodic orbits via Brouwer degree. Bull Sci Math 128:7–22

    Article  MathSciNet  MATH  Google Scholar 

  42. Matouk AE (2015) On the periodic orbits bifurcating from a fold Hopf bifurcation in two hyperchaotic systems, Opt Int J Light Electron Opt 126(24):4890–4895

    Article  Google Scholar 

  43. Ge SS, Wang C, Lee TH (2000) Adaptive backstepping control of a class of chaotic systems. Int J Bifurc 10:1149–1156

    MathSciNet  MATH  Google Scholar 

  44. Cai G, Huang J, Tian L, Wang Q (2006) Adaptive control and slow manifold analysis of a new chaotic system. Int J Nonlinear Sci 2(1):50–60

    Google Scholar 

  45. Sun M, Tian L, Jiang S, Xu J (2007) Feedback control and adaptive control of the energy resource chaotic system. Chaos Solitons Fract 32:168–180

    Article  MathSciNet  MATH  Google Scholar 

  46. Blasius B, Huppert A, Stone L (1999) Complex dynamics and phase synchronization in spatially extended ecological systems. Nature 399(6734):354–358

    Article  Google Scholar 

  47. Han SK, Kerrer C, Kuramoto Y (1995) Dephasing and bursting in coupled neural oscillators. Phys Rev Lett 75:3190–3193

    Article  Google Scholar 

  48. Lakshmanan M, Murali K (1996) Chaos in nonlinear oscillators: controlling and synchronization. World Scientific, Singapore

    Book  MATH  Google Scholar 

  49. Feki M (2003) An adaptive chaos synchronization scheme applied to secure communication. Chaos Solitons Fract 18:141–148

    Article  MathSciNet  MATH  Google Scholar 

  50. Murali K, Lakshmanan M (1998) Secure communication using a compound signal from generalized synchronizable chaotic systems. Phys Lett A 241(6):303–310

    Article  MATH  Google Scholar 

  51. Pecora LM, Carroll TL (1990) Synchronization in chaotic systems. Phys Rev Lett 64(8):821–824

    Article  MathSciNet  MATH  Google Scholar 

  52. Ott E, Grebogi C, Yorke JA (1990) Controlling chaos. Phys Rev Lett 64(11):1196–1199

    Article  MathSciNet  MATH  Google Scholar 

  53. Yassen MT (2006) Adaptive chaos control and synchronization for uncertain new chaotic dynamical system. Phys Lett A 350(1–2):36–43

    Article  MATH  Google Scholar 

  54. Agiza HN, Matouk AE (2006) Adaptive synchronization of Chua’s circuits with fully unknown parameters. Chaos Solitons Fract 28(1):219–227

    Article  MathSciNet  MATH  Google Scholar 

  55. Hegazi AS, Matouk AE (2013) Chaos synchronization of the modified autonomous Van der Pol-Duffing circuits via active control. Appl Chaos Nonlinear Dyn Sci Eng 3:185–202,Springer Berlin Heidelberg

  56. Park JH, Kwon OM (2005) A novel criterion for delayed feedback control of time-delay chaotic systems. Chaos Solitons Fract 23:495–501

    Article  MathSciNet  MATH  Google Scholar 

  57. Yang T, Chua LO (1998) Control of chaos using sampled-data feedback control. Int J Bifurc Chaos 8:2433–2438

    Article  MATH  Google Scholar 

  58. Konishi K, Hirai M, Kokame H (1998) Sliding mode control for a class of chaotic systems. Phys Lett A 245:511–517

    Article  Google Scholar 

  59. Yu Y, Zhang S (2004) Adaptive backstepping synchronization of uncertain chaotic system. Chaos Solitons Fract 21:643–649

    Article  MATH  Google Scholar 

  60. Matouk AE (2016) Chaos synchronization of a fractional-order modified Van der Pol- Duffing system via new linear control, backstepping control and Takagi-Sugeno fuzzy approaches. Complexity 21:116–124

    Article  MathSciNet  Google Scholar 

  61. Costello JS (1999) Synchronization of chaos in a generalized Lotka-Volterra attractor. Nonlinear J 1:11–17

    Google Scholar 

  62. Matouk AE (2010) Dynamical behaviors, linear feedback control and synchronization of the fractional order Liu system. J Nonlinear Syst Appl 1:135–140

    Google Scholar 

Download references

Acknowledgements

The authors thank the anonymous reviewers for providing some helpful comments which help to improve the presentation of this work.

Author information

Authors and Affiliations

  1. Department of Basic Science, Faculty of Computers and Informatics, Suez Canal University, Ismailia, 41522, Egypt

    A. A. Elsadany & A. G. Abdelwahab

  2. Mathematics Department, Faculty of Science, Mansoura University, Mansoura, 35516, Egypt

    A. E. Matouk

  3. Mansoura Higher Institute for Engineering and Technology, Damietta High Way, Mansourah, Egypt

    A. E. Matouk

  4. Department of Mathematics, Faculty of Science, Suez Canal University, Ismailia, Egypt

    H. S. Abdallah

Authors
  1. A. A. Elsadany
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. E. Matouk
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. G. Abdelwahab
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. H. S. Abdallah
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to A. A. Elsadany or A. E. Matouk.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Elsadany, A.A., Matouk, A.E., Abdelwahab, A.G. et al. Dynamical analysis, linear feedback control and synchronization of a generalized Lotka-Volterra system. Int. J. Dynam. Control 6, 328–338 (2018). https://doi.org/10.1007/s40435-016-0299-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-016-0299-x

Keywords

Search

Navigation