Skip to main content
SpringerLink
Log in

Large amplitude free flexural vibration of arbitrary thin plates using superparametric element

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

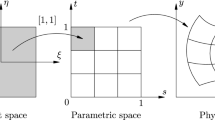
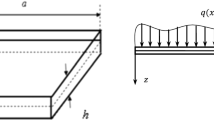
The large amplitude free flexural vibration of arbitrarily shaped thin plates is presented using finite element method. The formulation uses superparametric element which consists of an ACM plate element along with in-plane displacements for defining the displacement field and cubic serendipity element for geometry. This element avoids the inherent disadvantages of isoparametric elements when applied to thin plates. Von Karman’s large deflection theory is used, and the formulation is performed in the total Lagrangian coordinate system. The nonlinear equation is solved by direct iteration technique that uses the linear mode shape as starting vector. Nonlinear frequencies are obtained for different geometries and boundary conditions. Various numerical examples are shown to proof the versatility of the formulation, and its efficacy is shown by validating with published results. The results can be used in the field of aerospace, civil and naval engineering fields.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35
Fig. 36
Fig. 37
Fig. 38
Fig. 39
Fig. 40
Fig. 41
Fig. 42
Fig. 43
Fig. 44
Fig. 45
Fig. 46
Fig. 47
Fig. 48
Fig. 49
Fig. 50

Similar content being viewed by others

References

  1. El Bikri K, Benamar R, Bennouna M (2003) Geometrically non-linear free vibrations of clamped simply supported rectangular plates. Part I: the effects of large vibration amplitudes on the fundamental mode shape. Comput Struct 81:2029–2043

    Article  Google Scholar 

  2. Leung AYT, Zhu B (2004) Geometric nonlinear vibration of clamped Mindlin plates by analytically integrated trapezoidal p-element. Thin Walled Struct 42:931–945

    Article  Google Scholar 

  3. Haterbouch M, Benamar R (2003) The effects of large vibration amplitudes on the axisymmetric mode shapes and natural frequencies of clamped thin isotropic circular plates. Part I: iterative and explicit analytical solution for non-linear transverse vibrations. J Sound Vib 265:123–154

    Article  Google Scholar 

  4. Haterbouch M, Benamar R (2005) Geometrically nonlinear free vibrations of simply supported isotropic thin circular plates. J Sound Vib 280:903–924

    Article  Google Scholar 

  5. Kurpa L, Pilgun G, Ventsel E (2005) Application of the R-function method to nonlinear vibrations of thin plates of arbitrary shape. J Sound Vib 284:379–392

    Article  MATH  Google Scholar 

  6. Beidouri Z, Benamar R, Kadiri ME (2006) Geometrically non-linear transverse vibrations of C–S–S–S and C–S–C–S. Int J Non Linear Mech 41:57–77

    Article  MATH  Google Scholar 

  7. Wu WX, Shu C, Wang CM (2008) Mesh-free least-squares-based finite difference method for large-amplitude free vibration analysis of arbitrarily shaped thin plates. J Sound Vib 317:955–974

    Article  Google Scholar 

  8. Das D, Sahoo P, Saha K (2008) Large-amplitude dynamic analysis of simply supported skew plates by a variational method. J Sound Vib 313:246–267

    Article  Google Scholar 

  9. Taazount M, Zinai A, Bouazzouni A (2009) Large free vibration of thin plates: hierarchic finite element method and asymptotic linearization. Eur J Mech A Solids 28:155–165

    Article  MATH  Google Scholar 

  10. Belalia S, Houmat A (2010) Non-linear free vibration of elliptic sector plates by a curved triangular p-element. Thin Walled Struct 48:316–326

    Article  MATH  Google Scholar 

  11. Farbod A, Amabili A (2014) Non-linear static bending and forced vibrations of rectangular plates retaining non-linearities in rotations and thickness deformation. Int J Non Linear Mech 67:394–404

    Article  Google Scholar 

  12. Ivana U, Hrvoje S, Bernardin P (2015) A computationally efficient numerical model for a dynamic analysis of thin plates based on the combined finite-discrete element method. Eng Struct 101:509–517

    Article  Google Scholar 

  13. Jiang G, Li F, Li X (2016) Nonlinear vibration analysis of composite laminated trapezoidal plates. Steel Compos Struct 21(2):395–409

    Article  MathSciNet  Google Scholar 

  14. Adini A, Clough RW (1961) Analysis of plate bending by the finite element method. Report submitted to the National Science Foundation G7337

  15. Melosh RJ (1963) Basis for derivation of matrices for the direct stiffness method. AIAA J 1:1631–7

  16. Barik M, Mukhopadhyay M (1998) Finite element free flexural vibration analysis of arbitrary plates. Finite Elem Anal Des 29:137–151

    Article  MATH  Google Scholar 

  17. Zienkiewich OC, Taylor RL (1989) The finite element method. McGraw-Hill, London

    Google Scholar 

  18. Sheikh AH, Mukhopadhyay M (2004) Matrix and finite element analyses of structures. Ane Books Pvt. Ltd, New Delhi

    Google Scholar 

  19. Mallet R, Marcal P (1968) Finite element analysis of nonlinear structures. J Struct Div ASCE 94:2081–2105

    Google Scholar 

  20. Wood RD, Schrefler B (1978) Geometrically nonlinear analysis—a correlation of finite element methods. Int J Numer Methods Eng 12:635–642

    Article  MATH  Google Scholar 

  21. Barik M, Mukhopadhyay M (2002) A new stiffened plate element for the analysis of arbitrary plates. Thin Walled Struct 40:625–639

    Article  Google Scholar 

  22. Han W, Petyt M (1997) Geometrically nonlinear vibration analysis of thin, rectangular plates using the hierarchical finite element method-I: the fundamental mode of isotropic plates. Comput Struct 63(2):295–308

    Article  MATH  Google Scholar 

  23. Corr RB, Jennings E (1976) A simultaneous iteration algorithm for solution of symmetric eigenvalue problem. Int J Numer Methods Eng 10:647–663

    Article  MATH  Google Scholar 

  24. Chu HN, Herrmann G (1956) Influence of large amplitudes on free flexural vibrations of rectangular plates. J Appl Mech 23:532–540

    MATH  MathSciNet  Google Scholar 

  25. Rao GV, Raju IS, Raju KK (1976) A finite element formulations for large amplitude flexural vibrations of thin rectangular plates. Comput Struct 6:163–167

    Article  MATH  Google Scholar 

  26. Mei C, Narayanaswami N, Rao GV (1979) Large amplitude free flexural vibrations of thin plates of arbitrary shape. Comput Struct 10:675–681

    Article  MATH  Google Scholar 

  27. Yamaki N (1961) Influence of large amplitudes on free flexural vibrations of elastic plates. ZAMM 41:501–510

    Article  MATH  Google Scholar 

  28. Dong L (1991) Large amplitude vibration of thin annular plates. Appl Math Mech 12(6):583–593

    Article  MATH  Google Scholar 

  29. Singha MK, Ganapathi M (2004) Large amplitude free flexural vibrations of laminated composite skew plates. Int J Non Linear Mech 39:1709–1720

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, NIT, Rourkela, 769008, India

    Saleema Panda & Manoranjan Barik

Authors
  1. Saleema Panda
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Manoranjan Barik
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Saleema Panda.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Panda, S., Barik, M. Large amplitude free flexural vibration of arbitrary thin plates using superparametric element. Int. J. Dynam. Control 5, 982–998 (2017). https://doi.org/10.1007/s40435-016-0275-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-016-0275-5

Keywords

Search

Navigation