Skip to main content
SpringerLink
Log in

Dynamic response characteristics of axially moving plates subjected to moving load

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

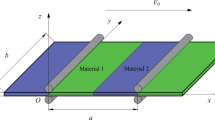
In this paper, the dynamic response of axially moving geometric nonlinear plates carrying moving mass is investigated. Based on von Kármán plate theory, the time-varying dynamic equation of the axially moving plate under moving loads is obtained by using the extended Hamiltonian principle and discretized into a set of finite-dimensional ordinary differential nonlinear equations by the assumed mode method. The equation incorporates the additional mass, damping, and stiffness matrix resulting from the inertia force, centrifugal force, and Coriolis force of the moving mass. Comparing the axially moving of plate, dynamic response results of linear and nonlinear results show the necessity of considering geometric nonlinearity in the model. The effects of system load parameters, including the mass of the moving load, the speed of the axially moving plate, and the plate’s aspect ratio on the vibration characteristics of the plate, are discussed. The dynamic responses of the axially moving plates under three different moving load trajectories are contrasted. Numerical results show that increasing the moving load mass and the speed of the axially moving plate leads to greater instability of the system, and the aspect ratio and different moving trajectories also have effects on the transverse vibration of the plate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Fryba L (1972) Vibration of solids and structures under moving loads. Noordhoff, Groningen

    Book  Google Scholar 

  2. Ouyang HJ (2011) Moving-load dynamic problems: a tutorial (with a brief overview). Mech Syst Signal Process 25(6):2039–2060

    Article  Google Scholar 

  3. Sheng GG, Wang X (2017) The geometrically nonlinear dynamic responses of simply supported beams under moving loads. Appl Math Model 48:183–195

    Article  MathSciNet  Google Scholar 

  4. Afras A, Ghoulbzouri AE (2023) Effect of linear and nonlinear stiffness support on the dynamic response of high-speed railway bridges. Structures 56:104982

  5. Abbas Z, Pedro M, Costin P, Raid K (2021) Free vibration of viscoelastically supported beam bridges under moving loads: closed-form formula for maximum resonant response. Eng Struct 244:112759

    Article  Google Scholar 

  6. Li HL, Wang TY, Wu G (2023) Nonlinear vibration analysis of beam-like bridges with multiple breathing cracks under moving vehicle load. Mech Syst Signal Process 186:109866

    Article  Google Scholar 

  7. Wang YW, Xie K, Fu TR, Shi CL (2019) Vibration response of a functionally graded graphene nanoplatelet reinforced composite beam under two successive moving masses. Compos Struct 209:928–939

    Article  Google Scholar 

  8. Hankari SEL, Dkiouak R, Roky K (2022) Resonance and cancellation phenomena in partially clamped simply supported beam bridges under moving trains. Structures 41:1247–1256

    Article  Google Scholar 

  9. Ebrahimi-Mamaghani A, Sarparast H, Rezaei M (2020) On the vibrations of axially graded Rayleigh beams under a moving load. Appl Math Model 84:554–570

    Article  MathSciNet  Google Scholar 

  10. Zhang Q, Liu H (2020) On the dynamic response of porous functionally graded microbeam under moving load. Int J Eng Sci 153:103317

    Article  MathSciNet  Google Scholar 

  11. Chen Y, Fu YM, Zhong J, Li YL (2017) Nonlinear dynamic responses of functionally graded tubes subjected to moving load based on a refined beam model. Nonlinear Dyn 88:1441–1452

    Article  Google Scholar 

  12. Ansari M, Esmailzadeh E, Younesian D (2010) Internal-external resonance of beams on non-linear viscoelastic foundation traversed by moving load. Nonlinear Dyn 61:163–182

    Article  Google Scholar 

  13. Ismail E (2020) Dynamics of size-dependant Timoshenko micro beams subjected to moving loads. Int J Mech Sci 175:105501

    Article  Google Scholar 

  14. Colmenares D, Andersson A, Karoumi R (2022) Closed-form solution for mode superposition analysis of continuous beams on flexible supports under moving harmonic loads. J Sound Vib 520:116587

    Article  Google Scholar 

  15. Liu ZH, Niu JC, Jia RH, Guo JC (2021) An efficient numerical method for dynamic analysis of polygonal plate under moving loads. Thin-Walled Structures 167:108183

    Article  Google Scholar 

  16. Liu ZH, Niu JC, Jia RH (2021) Dynamic analysis of arbitrarily restrained stiffened plate under moving loads. Int J Mech Sci 200:106414

    Article  Google Scholar 

  17. Jafari P, Kiani Y (2022) Analysis of arbitrary thick graphene platelet reinforced composite plates subjected to moving load using a shear and normal deformable plate model. Materials Today Communications 31:103745

    Article  Google Scholar 

  18. Tian YH, Li QY, Feng Y, Yu YG, Wu D, Chen XJ, Gao W (2023) Nonlinear dynamic analysis of the functionally graded graphene platelets reinforced porous plate under moving mass. Thin-Walled Structures 183:110363

    Article  Google Scholar 

  19. Praharaj RK, Datta N (2020) Dynamic response of plates resting on a fractional viscoelastic foundation and subjected to a moving load. Mech Bases Des Struct Mach 50(7):2317–2332

    Article  Google Scholar 

  20. Noroozi AR, Malekzadeh P (2023) Investigating nonlinear moving load responses of FG-GPLRC skew plates using meshfree radial point interpolation method. Compos Struct 308:116718

    Article  Google Scholar 

  21. Malekzadeh P, Monajjemzadeh SM (2015) Nonlinear response of functionally graded plates under moving load. Thin Walled Struct 96:120–129

    Article  Google Scholar 

  22. Fatehi P, Mahzoon M, Farid M (2021) Piezoelectric energy harvesting from nonlinear dynamics of functionally graded plate under multi-moving loads and masses. Mech Based Des Struct Mach 51(5):2515–2434

    Google Scholar 

  23. Sahoo PR, Barik M (2020) A numerical investigation on the dynamic response of stiffened plated structures under moving loads. Structures, 28:1675–1686

  24. Nikkhoo A, Hassanabadi ME, Azam SE, Amiri JV (2014) Vibration of a thin rectangular plate subjected to series of moving inertial loads. Mech Res Commun 55:105–113

    Article  Google Scholar 

  25. Eftekhari SA, Jafari AA (2012) Vibration of an initially stressed rectangular plate due to an accelerated traveling mass. Scientia Iranica 19(5):1195–1213

    Article  Google Scholar 

  26. Ghayesh MH, Amabili M, Païdoussis MP (2013) Nonlinear dynamics of axially moving plates. J Sound Vib 332(2):391–406

    Article  Google Scholar 

  27. Wang YB, Ding H, Chen LQ (2018) Nonlinear vibration of axially accelerating hyperelastic beams. Int J Non-Linear Mech 99:302–310

    Article  Google Scholar 

  28. Wang YB, Ding H, Chen LQ (2019) Vibration of axially moving hyperelastic beam with finite deformation. Appl Math Model 71:269–285

    Article  MathSciNet  Google Scholar 

  29. Qiao Y, Yao G (2022) Stability and nonlinear vibration of an axially moving plate interacting with magnetic field and subsonic airflow in a narrow gap. Nonlinear Dyn 110:3187–3208

    Article  Google Scholar 

  30. Zhang FY, Cao ZW, Qiao Y, Liu D, Yao G (2023) Parametric vibration stability analysis of an axially moving plate with periodical distributed materials. J Vib Eng Technol. https://doi.org/10.1007/s42417-022-00792-6

    Article  Google Scholar 

  31. Yang FL, Wang YQ, Liu YF (2022) Low-velocity impact response of axially moving functionally graded graphene platelet reinforced metal foam plates. Aerosp Sci Technol 123:107496

    Article  Google Scholar 

  32. Zhang DB, Tang YQ, Liang RQ, Yang L, Chen LQ (2021) Dynamic stability of an axially transporting beam with two-frequency parametric excitation and internal resonance. Eur J Mech A/Solids, 85:104084

  33. Ambili M (2008) Nolinear vibrations and stability of shells and plates. Cambridge University Press, New York

    Book  Google Scholar 

  34. Pirmoradian M, Torkan E, Karimpour H (2018) Parametric resonance analysis of rectangular plates subjected to moving inertial loads via IHB method. Int J Mech Sci 142–143:191–215

    Article  Google Scholar 

  35. Timoshenko S, Woinowsky-Krieger S (1959) Theory of plates and shells. McGraw-Hill Company, New York

    Google Scholar 

  36. Armagan K (2023) Transient vibration analysis of strain gradient multi-directional functionally graded microplates under a moving concentrated load. Compos Struct 308:116678

    Article  Google Scholar 

  37. Enshaeian A, Rofooei FR (2014) Geometrically nonlinear rectangular simply supported plates subjected to a moving mass. Acta Mech 225:595–608

  38. Song QH, Shi JH, Liu ZQ, Wan Y (2016) Dynamic analysis of rectangular thin plates of arbitrary boundary conditions under moving loads. Int J Mech Sci 117:16–29

    Article  Google Scholar 

  39. Yao G, Xie Z, Zhu L, Zhang Y (2021) Nonlinear vibrations of an axially moving plate in aero-thermal environment. Nonlinear Dyn 105:2921–2933

    Article  Google Scholar 

  40. Hatami S, Ronagh HR, Azhari M (2008) Exact free vibration analysis of axially moving viscoelastic plates. Comput Struct 86(17–8):1738–1746

    Article  Google Scholar 

  41. Yao G, Li FM (2016) Dynamics and stability of an axially moving plate interacting with surrounding airflow. Meccanica 51:2111–2119

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This research is supported by the Natural Science Foundation of Liaoning (2020-MS-092).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering and Automation, Northeastern University, Shenyang, 110819, China

    Mingjun Song & Guo Yao

  2. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin, 150001, China

    Yongheng Yu

Authors
  1. Mingjun Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guo Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yongheng Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guo Yao.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Technical Editor: Samuel da Silva.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Song, M., Yao, G. & Yu, Y. Dynamic response characteristics of axially moving plates subjected to moving load. J Braz. Soc. Mech. Sci. Eng. 46, 365 (2024). https://doi.org/10.1007/s40430-024-04949-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-024-04949-0

Keywords

Search

Navigation