Skip to main content
SpringerLink
Log in

Analytical and numerical solution of generalized static analysis of tall buildings: double-beam systems Timoshenko

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

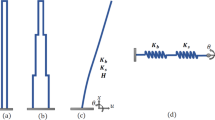
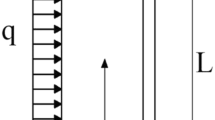
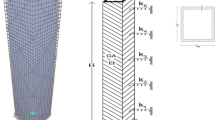
This article introduces a method for statically analyzing tall buildings using a combination of the continuum method and the transfer matrix method. The approach offers both analytical and numerical solutions, enabling the assessment of critical parameters such as lateral, rotational displacements, and drifts in tall buildings. The continuous model used consists of the parallel coupling of two Timoshenko beams. This model captures the interaction between flexural and shear stiffness, presenting a comprehensive understanding of tall building behavior. Moreover, it incorporates three distinct kinematic fields that encompass both translational and rotational movements. The flexibility of the model enables an expansive analysis across various structural configurations, including frames, shear walls, coupled shear walls, and tall buildings with complex structural systems. The equilibrium equations and essential boundary conditions are obtained by a variational approach based on Hamilton’s principle. For tall buildings with uniform properties along their height, a closed-form solution is proposed, while a numerical solution is presented for structures with varying geometric and structural properties along their height by analytically deriving their transfer matrix. Numerical demonstrations showcase the precision and reliability of the proposed analytical and numerical techniques. Furthermore, the method offers the advantage of reduced processing time, making it particularly suitable for preliminary analysis of tall buildings and serving as a valuable tool for verifying structural integrity and performance in later stages of the project.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

References

  1. Chitty L (1947) On the cantilever composed of a number of parallel beams interconnected by cross bars. Lond Edinb Dublin Philos Mag J Sci Ser 7:685–699. https://doi.org/10.1080/14786444708521646

    Article  MathSciNet  Google Scholar 

  2. Chitty L and Wan WY (1948) Tall building structures under wind load. In: Proceedings of the 7th International Congress for Applied Mechanics, 22, pp 254–268

  3. Skattum KS (1971) Dynamic analysis of coupled shear walls and sandwich beams, Earthquake Engineering Research Laboratory, California Institute of Technology, Pasadena. https://resolver.caltech.edu/CaltechThesis:10192017-151943526

  4. Rosman R (1973) Dynamics and stability of shear wall building structures. Proc Inst Civ Eng 55:411–423. https://doi.org/10.1680/iicep.1973.4875

    Article  Google Scholar 

  5. Rosman R (1981) Buckling and vibrations of spatial building structures. Eng Struct 4(3):191–202. https://doi.org/10.1016/0141-0296(81)90001-8

    Article  Google Scholar 

  6. Reinhorn A (1978) Static and Dynamic Torsional Coupling in Tall Buildings. In: PhD thesis, Israel Institute of Technology-Israel

  7. Hegedűs I, Kollár LP (1984) Buckling of sandwich columns with thick faces subjecting to axial loads of arbitrary distribution. Acta Technica Scientiarum Hungaricae 97:123–132

    Google Scholar 

  8. Miranda E (1999) Approximate lateral drift demands in multi-story buildings subjected to earthquakes. J Struct Eng 124(4):417–425. https://doi.org/10.1061/(ASCE)0733-9445(2002)128:7(840)

    Article  Google Scholar 

  9. Zalka KA (2002) Buckling analysis of buildings braced by frameworks, shear walls and cores. Struct Design Tall Spec Build 11(3):197–219. https://doi.org/10.1002/tal.194

    Article  Google Scholar 

  10. Hans S (2002) Dynamic auscultation of buildings and modeling by homogenization contribution to the analysis of seismic vulnerability. In: Ph.D. Dissertation, National Institute of Applied Sciences of Lyon

  11. Potzta G, Kollár LP (2003) Analysis of building structures by replacement sandwich beams. Int J Solids Struct 40(3):535–553. https://doi.org/10.1016/S0020-7683(02)00622-4

    Article  Google Scholar 

  12. Bozdogan KB, Ozturk D, Nuhoglu A (2007) An approximate method for static and dynamic analyses of multi-bay coupled shear walls. Struct Design Tall Spec Build 18(1):1–12. https://doi.org/10.1002/tal.390

    Article  Google Scholar 

  13. Zalka KA (2007) A simple method for the deflection analysis of tall wall-frame building structures under horizontal load. Struct Design Tall Spec Build 18(3):291–311. https://doi.org/10.1002/tal.410

    Article  Google Scholar 

  14. Kaviani P, Rahgozar R, Saffari H (2008) Approximate analysis of tall buildings using sandwich beam models with variable cross-section. Struct Design Tall Special Build 17:401–418. https://doi.org/10.1002/tal.360

    Article  Google Scholar 

  15. Bozdogan KB, Ozturk D (2010) An approximate method for lateral stability analysis of wall-frame buildings including shear deformations of walls. Sadhana 35(3):241–253. https://doi.org/10.1007/s12046-010-0008-y

    Article  Google Scholar 

  16. Chesnais C (2010) Dynamics of unbraced reticular media: application to buildings. In: Ph.D. Dissertation, Central School of Lyon

  17. Bozdogan KB (2010) Static, dynamic and stability analyses of multi storey building using transfer matrix method. In: Ph.D. Dissertation, Ege University

  18. Zalka KA (2013) Maximum deflection of symmetric wall-frame buildings. Periodica Polytechnica Civ Eng 2(57):173–184. https://doi.org/10.3311/PPci.7172

    Article  Google Scholar 

  19. Moghadasi H (2015) Replacement beam methods in analysis of tall building structural systems. In: Ph.D. Dissertation, Politecnico di Milano

  20. Laier JE (2021) An improved continuous medium technique for three-dimensional analysis of tall building structures. Struct Eng Mechan 80(1):73–81. https://doi.org/10.12989/sem.2021.80.1.073

    Article  Google Scholar 

  21. Franco C (2021) Modélisation multi-échelle de la réponse seismique des bâtiments: couplage homogénéisation et éléments multifibras. In: Ph.D. Dissertation, Université Gustave Eiffel

  22. Franco C, Chesnais C, Semblat JF, Giry C, Desprez C (2022) Finite element formulation of a homogenized beam for reticulated structure dynamics. Comput Struct. https://doi.org/10.1016/j.compstruc.2021.106729

    Article  Google Scholar 

  23. Pinto MC (2023) Closed-form and numerical solution of the static and dynamic analysis of coupled shear walls by the continuous method and the modified transfer matrix method. Struct Eng Mechan 86(1):49–68. https://doi.org/10.12989/sem.2023.86.1.049

    Article  Google Scholar 

  24. Pinto MC (2023) A general simplified method for static and free vibration analysis of coupled shear walls of a bay. Mechan Based Design Struct Machin. https://doi.org/10.12989/sem.2023.86.1.049

    Article  Google Scholar 

  25. Pinto MC (2023) A novel generalized sandwich-type replacement beam for static analysis of tall buildings: inclusion of local shear deformation of walls. Thin-Walled Struct 190:110967. https://doi.org/10.12989/sem.2023.86.1.049

    Article  Google Scholar 

  26. Pinto MC (2023) Generalized sandwich beam for global stability analysis of tall buildings with shear walls using a modified transfer matrix method. Int J Struct Stabil Dyn. https://doi.org/10.1142/S0219455424500378

    Article  Google Scholar 

  27. Timoshenko S (1921) On the correction for shear of the differential equation for transverse vibrations of prismatic bar. Phil Mag 41:744–746

    Article  Google Scholar 

Download references

Acknowledgements

The research described in this document was possible thanks to the support of Jesus Christ. The author wants to dedicate this research to his brilliant daughter Zoé Juliette Pinto (my beautiful girl). The author acknowledges the support from the Multiphysics Modeling and Simulation Group at Institute Tecgraf PUC-Rio.

Author information

Authors and Affiliations

  1. Department of Civil and Environmental Engineering, Pontifical Catholic University of Rio de Janeiro, Rio de Janeiro, Brazil

    Mao Cristian Pinto-Cruz

  2. Department of Civil Engineering, National University of Engineering, Lima, Peru

    Mao Cristian Pinto-Cruz

Authors
  1. Mao Cristian Pinto-Cruz
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

MCPC contributed to writing—review and editing, writing—original draft, visualization, validation, supervision, resources, project administration, methodology, investigation, funding acquisition, formal analysis, data curation and conceptualization and provided software.

Corresponding author

Correspondence to Mao Cristian Pinto-Cruz.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Technical Editor: Andre T. Beck.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (DOCX 90 KB)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pinto-Cruz, M.C. Analytical and numerical solution of generalized static analysis of tall buildings: double-beam systems Timoshenko. J Braz. Soc. Mech. Sci. Eng. 46, 368 (2024). https://doi.org/10.1007/s40430-024-04809-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-024-04809-x

Keywords

Search

Navigation