Skip to main content
SpringerLink
Log in

Robotic arm time–jerk optimal trajectory based on improved dingo optimization

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

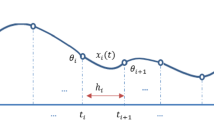
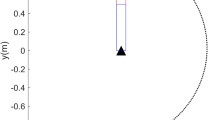
Abstract

Time and jerk are two pivotal factors in the optimal trajectory planning of a manipulator. A trajectory that minimizes time and jerk can ensure smooth and efficient operation of the manipulator. This paper introduces a novel, general time–jerk optimization method for manipulators, which integrates quintic non-uniform rational B spline (QNURBS) with an improved dingo optimization algorithm based on simulated annealing, namely SA-DOA. This method has been successfully applied to plan the time–jerk optimal trajectory of the Kinova Jaco2 robot arm. With maximum angular velocity, acceleration, and jerk as constraints, and running time and total jerk as optimization objectives, the method employs SA-DOA to determine the optimal time interval and then utilizes QNURBS to generate the angle curves of the six joints in joint space, based on the specified path point and optimal time interval. Experimental results demonstrate that SA-DOA can obtain the global optimal solution within a limited number of iterations. Compared with dingo optimization algorithm (DOA), particle swarm optimization algorithm (PSO), and simulated annealing (SA), the optimization results have improved by 26.57%, 21.87%, and 0.26%, respectively. The time–jerk optimal motion trajectory enhances the execution efficiency of the manipulator and produces less jerk during movement, thereby improving motion control performance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Du ZJ, Liang YL, Yan ZY, Sun LL, Chen W (2021) Human-robot interaction control of a haptic master manipulator used in laparoscopic minimally invasive surgical robot system. Mech Mach Theory 156:104132

    Article  Google Scholar 

  2. Angel SD, Ulises ZC, J Alfonso PG, Xiomara ZC (2019) Operation of a haptic interface for offline programming of welding robots by applying a spring-damper model. Int J Comput Integr Manuf 32(11):1098–1116

    Article  Google Scholar 

  3. Barbosa WS, Gioia MM, Natividade VG, Wanderley RF, Chaves MR, Gouvea FC, Goncalves FM (2020) Industry 4.0: examples of the use of the robotic arm for digital manufacturing processes. Int J Interact Des Manuf 14:1569–1575. https://doi.org/10.1007/s12008-020-00714-4

    Article  Google Scholar 

  4. Li X, Zhao H, He X, Ding H (2023) A novel cartesian trajectory planning method by using triple NURBS curves for industrial robots. Robot Comput-Integr Manuf 83:102576. https://doi.org/10.1016/j.rcim.2023.102576

    Article  Google Scholar 

  5. Wang H, Heng W, Huang J, Zhao B, Quan L (2019) Smooth point-to-point trajectory planning for industrial robots with kinematical constraints based on high-order polynomial curve. Mech Mach Theory 139:284–293. https://doi.org/10.1016/j.mechmachtheory.2019.05.002

    Article  Google Scholar 

  6. Dikra EH, Badreddine A, Larbi EB, Jalal EB (2019) Optimal trajectory planning for spherical robot using evolutionary algorithms. Procedia Manuf 32:960–968. https://doi.org/10.1016/j.promfg.2019.02.309

    Article  Google Scholar 

  7. Lv Y, Peng Z, Qu C, Zhu D (2020) An adaptive trajectory planning algorithm for robotic belt grinding of blade leading and trailing edges based on material removal profile model. Robot Comput-Integr Manuf 66:101987. https://doi.org/10.1016/j.rcim.2020.101987

    Article  Google Scholar 

  8. Miao X, Fu H, Song X (2022) Research on motion trajectory planning of the robotic arm of a robot. Artif Life Robot 27:561–567. https://doi.org/10.1007/s10015-022-00779-2

    Article  Google Scholar 

  9. Ekrem Ö, Aksoy B (2023) Trajectory planning for a 6-axis robotic arm with particle swarm optimization algorithm. Eng Appl Artif Intell 122:106099. https://doi.org/10.1016/j.engappai.2023.106099

    Article  Google Scholar 

  10. Fang Y, Qi J, Hu J, Wang W, Peng Y (2020) An approach for jerk-continuous trajectory generation of robotic manipulators with kinematical constraints. Mech Mach Theory 153:103957. https://doi.org/10.1016/j.mechmachtheory.2020.103957

    Article  Google Scholar 

  11. Shrivastava A, Dalla VK (2023) A fast and unified method to find a minimum-jerk robot joint trajectory using particle swarm optimization. Arab J Sci Eng 48:2687–2699. https://doi.org/10.1007/s13369-022-07002-1

    Article  Google Scholar 

  12. Wu H, Yang J, Huang S, Ning X, Zhang Z (2023) Multi-objective adaptive trajectory optimization for industrial robot based on acceleration continuity constraint. Robot Comput-Integr Manuf 84:102597. https://doi.org/10.1016/j.rcim.2023.102597

    Article  Google Scholar 

  13. Huang J, Hu P, Wu K, Zeng M (2018) Optimal time-jerk trajectory planning for industrial robots. Mech Mach Theory 121:530–544. https://doi.org/10.1016/j.mechmachtheory.2017.11.006

    Article  Google Scholar 

  14. Chen W, Wang H, Liu Z, Jiang K (2023) Time-energy-jerk optimal trajectory planning for high-speed parallel manipulator based on quantum-behaved particle swarm optimization algorithm and quintic B-spline. Eng Appl Artif Intell 126:107223. https://doi.org/10.1016/j.engappai.2023.107223

    Article  Google Scholar 

  15. Karahan O, Karci H, Tangel A (2022) Optimal trajectory generation in joint space for 6r industrial serial robots using cuckoo search algorithm. Intel Serv Robot 15:627–648. https://doi.org/10.1007/s11370-022-00440-8

    Article  Google Scholar 

  16. Zhang MS, Xiao JZ, Wang EH, Zhuang Q (2021) Inverse kinematical solving and trajectory planning of redundant manipulator. J Mech Transm 45(6):71–76

    Google Scholar 

  17. Zheng T, Liu ML (2020) A method of segmental interpolation trajectory planning for robotic arm. Mach Des Manuf 3:261–264. https://doi.org/10.19356/j.cnki.1001-3997.2020.03.063

    Article  Google Scholar 

  18. Peiper DL (1968) The kinematics of manipulators under computer control. Phd Thesis, Stanford University

  19. Liu C, Yang L, Zhang L (2021) Polynomial accelerated iterative approximation for higher order and rational Bézier curves. Results Math 76:138

    Article  Google Scholar 

  20. Xie WS, Zhang S (2007) Generalized B-splines and knot insertion algorithm. J East China Univ Sci Technol 1:141–144. https://doi.org/10.14135/j.cnki.1006-3080.2007.01.032

    Article  Google Scholar 

  21. Han J, Moraga C (1995) The influence of the sigmoid function parameters on the speed of backpropagation learning. In: Mira J, Sandoval F (eds) Paper presented at the From Natural to Artificial Neural Computation. IWANN 1995. Lecture Notes in Computer Science, vol 930. Springer, Berlin, Heidelberg

  22. Hernán PV, Delgado AFP, Gustavo EC, Ana Beatriz MC, Jonás VA, Fernando RP (2021) A bio-inspired method for engineering design optimization inspired by dingoes hunting strategies. Math Probl Eng 2021:9107547

    Google Scholar 

  23. Kirkpatrick S, Gelatt CD Jr, Vecchi MP (1983) Optimization by simulated annealing. Science 220(4598):671–680

    Article  MathSciNet  Google Scholar 

Download references

Funding

This work was supported by [Open Project of China International Science and Technology Cooperation Base on Intelligent Equipment Manufacturing in Special Service Environment](Grant numbers [ISTC2021KF07] and [ISTC2021KF08]), and by [China National Key Research and Development Project] (Grant number [2017YFE0113200]), and by [Anhui University of Technology youth Fund] (Grant number [QZ202217]).

Author information

Author notes

  1. Xiang-rong Xu, Qi-qi Li and Hui Zhang have been contributed equally to this work.

Authors and Affiliations

  1. School of Mechanical Engineering, Anhui University of Technology, Maxiang Road, Ma’anshan, 243032, Anhui Province, China

    Quan-cheng Pu, Xiang-rong Xu, Qi-qi Li & Hui Zhang

Authors
  1. Quan-cheng Pu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiang-rong Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qi-qi Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hui Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by [QP], [XX], [QL], and [HZ]. The first draft of the manuscript was written by [QP] and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Xiang-rong Xu.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Technical Editor: Adriano Almeida Gonçalves Siqueira.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pu, Qc., Xu, Xr., Li, Qq. et al. Robotic arm time–jerk optimal trajectory based on improved dingo optimization. J Braz. Soc. Mech. Sci. Eng. 46, 198 (2024). https://doi.org/10.1007/s40430-024-04694-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-024-04694-4

Keywords

Search

Navigation