Skip to main content
SpringerLink
Log in

Mesh stiffness model of a spur gear pair with surface roughness in mixed elastohydrodynamic lubrication

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

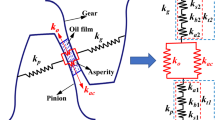
The calculation of time-varying mesh stiffness for gear meshing in mixed EHL regime is of great importance to the accurate evaluation of tooth damage, contact fatigue life and wear performance of a gear transmission system. In this work, the mesh stiffness of a spur gear pair in mixed elastohydrodynamic line (EHL) contact is established in conjunction with a revised contact stiffness to include the effect of surface roughness and oil film. The revised contact stiffness of gear tooth surface in EHL contact is developed by combining the stiffness of both the rough gear tooth and liquid film based on the load-sharing concept, which is used to replace the Hertzian contact stiffness of ideal smooth cylinders in traditional gear mesh stiffness. To include the effect of tooth curvature on the asperity distribution at the gear tooth surface, the cylindrical contact coefficient is introduced and incorporated into the statistical micro-contact Greenwood and Williamson model (GW model) to derive the stiffness of rough curved gear tooth contact. The film thickness equation for mixed EHL line contact is employed together with the lubricant bulk modulus to predict the liquid film stiffness at different mesh positions. Effects of surface roughness, input torque, rotating speed and lubricant on the contact stiffness and EHL mesh stiffness are analyzed. Results show that the lubricant film stiffness is much higher than the solid part, especially at tip or root position. The fluctuation of mesh stiffness in single-to-double teeth contact is smaller than that calculated using Hertzian contact model, indicating a better transmission stationarity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Abbreviations

A n :

nominal contact area between two rough flat surfaces, m2

A i :

equivalent cross-sectional area, m2

B :

bulk modulus, GPa

B 0 :

bulk modulus at ambient pressure, GPa

\(B_{0}^{\prime }\) :

pressure change rate at ambient pressure, GPa/s

B 00 :

bulk modulus at ambient pressure and absolute zero temperature, GPa

d d :

distance between mean of summit heights and that of surface heights, m

d i :

distance from the load point to the micro-element, m

d n :

dimensionless distance between the mean of summit heights and that of the surface heights, dn = dd/σ

E 1 E 2 E :

modulus of elasticity of first and second cylinder and the effective modulus of elasticity, GPa

e i :

cross-sectional width of the micro-element, m

F :

normal load, N

F C :

asperity load, N

F H :

fluid load, N

\(\overline{F}\) :

dimensionless normal load, \(\overline{F} = \sqrt {\frac{{4\pi L_{c} RE}}{F}}\)

G :

equivalent shear modulus, GPa

G 1 ,G 2 :

shear modulus of first and second cylinder, GPa

G c :

dimensionless material parameter

H :

separation of the mean line of the rough surface and the flat surface, m

h n :

dimensionless separation, hn = h/σ

\(\overline{h}\) :

dimensionless film thickness, \(\overline{h} = \frac{h}{R}\)

I i :

equivalent cross-sectional modulus, GPa

K a :

solid asperity contact stiffness, N/m

k a :

axial compressive stiffness, N/m

k b :

bending stiffness, N/m

k c :

contact stiffness of the gear pair, N/m

k f :

stiffness due to the fillet foundation deflection, N/m

k g :

stiffness of the contact asperities at gear tooth surfaces, N/m

k h :

Hertzian contact stiffness between ideal smooth cylinders, N/m

k l :

stiffness of the lubricant film, N/m

k s :

shear stiffness, N/m

L :

tooth width, mm

N :

total number of asperities

N c :

total number of asperities deformed at curved meshing surface

n :

rotating speed, r/min

n s :

asperity distribution density, m−2

n g :

dimensionless asperity density, \(n_{g} = n_{s} R\sqrt {\beta R}\)

R 1 R 2 R :

radius of first and second cylinder and the effective radius, m

T t :

Temperature, K

u :

relative motion velocity, m/s

v :

Poisson’s ratio

v 1 v 2 :

Poisson’s ratio of cylinders

W :

dimensionless load

z :

asperity height measured from the mean line of summit heights, m

α :

pressure–viscosity coefficient, GPa−1

α 1 :

pressure angle, deg

β :

asperity radius, μm

ω 1, ω 2 :

angular speed of first and second cylinder, rad/s

γ 1, γ 2 :

scaling factors for hydrodynamic part and asperity contact part

σ :

standard deviation of the surface heights distribution

σ s :

standard deviation of asperity heights distribution

σ sn :

dimensionless standard deviation of asperity heights, σsn = σs/R

β k :

Tait-Doolittle model constant

λ :

film thickness parameter, λ = h/σs

λ c :

cylindrical contact coefficient

η 0 :

inlet viscosity, Pa s

\(\phi (z)\) :

probability density function of Gaussian distribution

\(\phi_{n} (z_{n} )\) :

dimensionless standard normal distribution function

References

  1. Akbarzadeh S, Khonsari MM (2010) On the prediction of running-in behavior in mixed-lubrication line contact. ASME J Tribol 32:032102–032112

    Article  Google Scholar 

  2. Simon V V (2019) Improved mixed elastohydrodynamic lubrication of hypoid gears by the optimization of manufacture parameters. Wear 438–439: 102722.

  3. Wang ZZ, Pu W, He T, Wang JX, Cao W (2019) Numerical simulation of transient mixed elastohydrodynamic lubrication for spiral bevel gears. Tribol Int 139:67–77

    Article  Google Scholar 

  4. Chen KK, Huangfu YF, Ma H, Xu ZT, Li X, Wen BC (2019) Calculation of mesh stiffness of spur gears considering complex foundation types and crack propagation paths. Mech Syst Signal Process 130:273–292

    Article  Google Scholar 

  5. Chen ZG, Zhai WM, Wang KY (2019) Vibration feature evolution of locomotive with tooth root crack propagation of gear transmission system. Mech Syst Signal Process 115:29–44

    Article  Google Scholar 

  6. Chen ZG, Zhou ZW, Zhai WM, Wang KY (2020) Improved mesh stiffness calculation model of spur gear pair with tooth profile deviations. Mech Mach Theory 149: 103838.

  7. Meng Z, Shi GX, Wang FL (2020) Vibration response and fault characteristics analysis of gear based on time-varying mesh stiffness. Mech Mach Theory 148: 103786.

  8. Zhou CJ, Xiao ZL (2018) Stiffness and damping models for the oil film in line contact elastohydrodynamic lubrication and applications in the gear drive. Appl Math Model 61:634–649

    Article  MathSciNet  Google Scholar 

  9. Xiao ZL, Shi X (2019) Investigation on stiffness and damping of transient non-Newtonian thermal elastohydrodynamic point contact for crowned herringbone gears. Tribol Int 137:102–112

    Article  Google Scholar 

  10. Pei X, Pu W, Wang ZZ (2021) Contact stiffness and dynamic behavior caused by surface defects of spiral bevel gear in mixed lubrication. Eng Failure Anal 121:105129.

  11. Zhou CJ, Xiao ZL, Chen SY, Han X (2017) Normal and tangential oil film stiffness of modified spur gear with non-Newtonian elastohydrodynamic lubrication. Tribol Int 109:319–327

    Article  Google Scholar 

  12. Ouyang TC, Huang GC, Chen JX, Gao BX, Chen N (2019) Investigation of lubricating and dynamic performances for high-speed spur gear based on tribo-dynamic theory. Tribol Int 136:421–431

    Article  Google Scholar 

  13. Shi XJ, Sun W, Lu XQ, Ma X, Zhu D, Zhao B, He T (2019) Three-dimensional mixed lubrication analysis of spur gears with machined roughness. Tribol Int 140: 105864.

  14. Li ZF, Zhu CC, Liu HJ, Gu ZL (2020) Mesh stiffness and nonlinear dynamic response of a spur gear pair considering tribo-dynamic effect. Mech Mach Theory 153:103989.

  15. Johnson KL, Greenwood JA, Poon SY (1972) Simple theory of asperity contact in elastohydrodynamic lubrication. Wear 19:91–108

    Article  Google Scholar 

  16. Gelinck ERM, Schipper DJ (2000) Calculation of stribeck curves for line contacts. Tribol Int 33:175–181

    Article  Google Scholar 

  17. Lu XB, Khonsari MM, Gelinck ERM (2006) The stribeck curve: experimental results and theoretical prediction. ASME Journal of Tribology 128:789–794

    Article  Google Scholar 

  18. Dwyer-Joyce RS, Reddyhoff T, Zhu J (2011) Ultrasonic measurement for film thickness and solid contact in elastohydrodynamic lubrication. ASME J Tribol 133:031501.

  19. Beheshti A, Khonsari MM (2013) An engineering approach for the prediction of wear in mixed lubricated contacts. Wear 308:121–131

    Article  Google Scholar 

  20. Xiao HF, Sun YY (2019) On the normal contact stiffness and contact resonance frequency of rough surface contact based on asperity micro-contact statistical models. Euro J Mech A/Solids 75:450–460

    Article  MathSciNet  Google Scholar 

  21. Sun YY, Xiao HF, Xu JW, Yu WN (2018) Study on the normal contact stiffness of the fractal rough surface in mixed lubrication. Proc Inst Mech Eng J J Eng Tribol 232(12):1604–1617

    Article  Google Scholar 

  22. Sun YY, Chuang H-C, Xiao HF, Xu JW (2020) Prediction of the normal contact stiffness between rough surfaces in lubricated contact via an equivalent thin layer. J Vib Control 26(21–22):2060–2069

    Article  MathSciNet  Google Scholar 

  23. Xiao HF, Sun YY, Xu JW (2018) Investigation into the normal contact stiffness of rough surface in line contact mixed elastohydrodynamic lubrication. Tribol Trans 61(4):742–753

    Article  Google Scholar 

  24. Greenwood JA, Williamson JBP (1966) Contact of nominally flat surfaces. Proc R Soc Lond Ser A 295:300–319

    Article  Google Scholar 

  25. Ma H, Zeng J, Feng RJ, Pang X, Wen BC (2016) An improved analytical method for mesh stiffness calculation of spur gears with tip relief. Mech Mach Theory 98:64–80

    Article  Google Scholar 

  26. Chen ZG, Zhang J, Zhai WM, Wang YW, Liu JX (2017) Improved analytical methods for calculation of gear tooth fillet-foundation stiffness with tooth root crack. Eng Fail Anal 82:72–81

    Article  Google Scholar 

  27. Sainsot P, Velex P, Duverger O (2004) Contribution of gear body to tooth deflections-a new bidimensional analytical formula. ASME J Mech Des 126:748–752

    Article  Google Scholar 

  28. Knyazeva M, Vasquez RJ, Gondecki L, Weibring M, Pöhl F, Kipp M, Tenberge P, Theisen W, Walther F, Biermann D (2018) Micro-magnetic and microstructural characterization of wear progress on case-hardened 16MnCr5 gear wheels. Materials 11:2290

    Article  Google Scholar 

  29. Chen Q, Xu F, Liu P, Fan H (2016) Research on fractal model of normal contact stiffness between two spheroidal joint surfaces considering friction factor. Tribol Int 97:253–264

    Article  Google Scholar 

  30. Johnson K (1985) Contact mechanics. Cambridge University Press, Cambridge

    Book  Google Scholar 

  31. Gonzalez-Valadez M, Baltazar A, Dwyer-Joyce RS (2010) Study of interfacial stiffness ratio of a rough surface in contact using a spring model. Wear 268:373–379

    Article  Google Scholar 

  32. Mulvihill DM, Brunskill H, Kartal ME, Dwyer-Joyce RS, Nowell D (2013) A comparison of contact stiffness measurements obtained by the digital image correlation and ultrasound techniques. Exp Mech 53:1245–1263

    Article  Google Scholar 

  33. Starzynski G, Buczkowski R (2014) Ultrasonic measurements of contact stiffness between rough surfaces. ASME J Tribol 136:034503-1–34505

    Article  Google Scholar 

  34. Xiao HF, Sun YY (2018) An improved virtual material based acoustic model for contact stiffness measurement of rough interface using ultrasound technique. Int J Solids Struct 155:240–247

    Article  Google Scholar 

  35. Masjedi M, Khonsari MM (2012) Film thickness and asperity load formulas for line-contact Elastohydrodynamic lubrication with provision for surface roughness. ASME J Tribol 134: 011503.

  36. Nuri KA, Halling J (1975) The normal approach between rough flat surfaces in contact. Wear 32:81–93

    Article  Google Scholar 

  37. Raghuwanshi NK, Parey A (2017) Experimental measurement of spur gear mesh stiffness using digital image correlation technique. Measurement 111:93–104

    Article  Google Scholar 

  38. Akbarzadeh S, Khonsari MM (2008) Thermoelastohydrodynamic analysis of spur gears with consideration of surface roughness. Tribol Lett 32:129–141

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China [Grant number 51775037].

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing, 100083, People’s Republic of China

    Huifang Xiao, Jinshan Gao & Jiazhou Wu

Authors
  1. Huifang Xiao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jinshan Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jiazhou Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Huifang Xiao.

Additional information

Technical Editor: Zilda de Castro Silveira.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xiao, H., Gao, J. & Wu, J. Mesh stiffness model of a spur gear pair with surface roughness in mixed elastohydrodynamic lubrication. J Braz. Soc. Mech. Sci. Eng. 44, 136 (2022). https://doi.org/10.1007/s40430-022-03397-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-022-03397-y

Keywords

Search

Navigation