Skip to main content
SpringerLink
Log in

The effect of thixotropy on dam-break flow: a numerical study by smoothed particle hydrodynamics

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

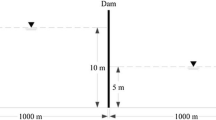
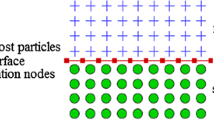
In this paper, the unsteady two-dimensional dam-break flow of Newtonian and thixotropic fluids is numerically investigated by smoothed particle hydrodynamics. In this method, the flow domain is replaced by several representative particles, and the mass and momentum conservation equations are solved in a Lagrangian framework for each representative particle. First, the Newtonian and shear-thinning cases are verified with previous numerical and experimental published results. Then, the dam-break flow of a thixotropic liquid obeying Moore’s rheological model is simulated. Several simulations are performed to investigate the effects of the model parameters. Furthermore, the differences between Newtonian and thixotropic fluid flow (including free surface shape and leading edge) are investigated. It is shown that the thixotropic behavior of fluids could dramatically affect the free surface shape and spreading speed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Cochard C, Ancey C (2009) Experimental investigation of the spreading of viscoplastic fluids on inclined planes. J Non-Newton Fluid Mech 158:73

    Article  Google Scholar 

  2. Moore F (1959) The rheology of ceramic slips and bodies. Trans Br Ceram Soc 58:470

    Google Scholar 

  3. Tehrani A (2008) Thixotropy in water-based drilling fluids. Ann Trans Nordic Rheol Soc 16:1

    Google Scholar 

  4. De Souza Mendez PR (2009) Modeling the thixotropic behavior of structured fluids. J Non-Newton Fluid Mech 164:66

    Article  Google Scholar 

  5. Ahmadpour A, Amini-Kafiabad H, Sadeghy K (2013) Dynamics of gas bubbles surrounded by Dullaert-Mewis thixotropic fluid. Nihon Reoroji Gakk (J Soc Rheol Jpn) 41:309

    Article  Google Scholar 

  6. Martin JC, Moyce WJ (1952) An experimental study of the collapse of liquid columns on a rigid horizental plane. Philos Trans R Soc Lond 244:312

    Article  Google Scholar 

  7. Piau JM, Debiane K (2005) Consistometers rheometry of power-law viscous fluids. J Non-Newton Fluid Mech 127:213

    Article  Google Scholar 

  8. Liu Y, Balmforth NJ, Hormozi S (2018) Axisymmetric viscoplastic dambreaks and the slump test. J Non-Newton Fluid Mech 258:45

    Article  MathSciNet  Google Scholar 

  9. Shadloo MS, Oger G, Le Touze D (2016) Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput Fluids 136:11

    Article  MathSciNet  Google Scholar 

  10. Lio GR, Lio MB (2003) Smoothed particle hydrodynamics: a meshfree particle method. World Scientific publishing, Singapore

    Book  Google Scholar 

  11. Shao S, Lo EYM (2003) Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv Water Res 26:787

    Article  Google Scholar 

  12. Roubtsova V, Kahawita R (2006) The SPH technique applied to free surface flows. Comput Fluids 35:1359

    Article  Google Scholar 

  13. Dalrymple RA, Rogers BD (2006) Numerical modeling of water waves with the SPH method. Coastal Eng 53:141

    Article  Google Scholar 

  14. Hosseini SM, Manzari MT, Hannani SK (2007) A fully explicit three‐step SPH algorithm for simulation of non‐Newtonian fluid flow. Int J Numer Methods Heat Fluid Flow 17:715

    Article  MathSciNet  Google Scholar 

  15. Molteni D, Colagrossi A (2009) A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH. Comput Phys Commun 180:861

    Article  MathSciNet  Google Scholar 

  16. Xu X (2016) An improved SPH approach for simulating 3D dam-break flows with breaking waves. Comput Methods Appl Mech Eng 311:723

    Article  MathSciNet  Google Scholar 

  17. Kermani E, Qiu T (2018) Simulation of quasi-static and dynamic collapses of rectangular granular columns using smoothed particle hydrodynamics method. Int J Geomech 18:04018113

    Article  Google Scholar 

  18. Kermani E, Qiu T (2020) Simulation of quasi-static axisymmetric collapse of granular columns using smoothed particle hydrodynamics and discrete element methods. Acta Geotech 15:423

    Article  Google Scholar 

  19. Chanson H, Jarny S, Coussot P (2006) Dam break wave of thixotropic fluid. J Hyd Eng 280:280

    Article  Google Scholar 

  20. Vahabi M, Sadeghy K (2013) Simulating bubble shape during its rise in Carreau-Yasuda fluids using WC-SPH method. Nihon Reoroji Gakk 41:319

    Article  Google Scholar 

  21. Sadeghy K, Vahabi M (2016) The effect of thixotropy on a rising gas bubble: a numerical study. Korea-Aust Rheol J 28:207

    Article  Google Scholar 

  22. Vahabi M, Sadeghy K (2014) On the use of SPH method for simulating gas bubbles rising in viscoelastic liquids. Nihon Reoroji Gakk 42:309

    Article  Google Scholar 

  23. Colagrossi A, Landrini M (2003) Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J Comput Phys 191:448

    Article  Google Scholar 

  24. Vahabi M, Kamkari B (2019) Simulating gas bubble shape during its rise in a confined polymeric solution by WC-SPH. Eur J Mech B/Fluids 75:1

    Article  MathSciNet  Google Scholar 

  25. Monaghan JJ (1994) Simulating free surface flows with SPH. J Comput Phys 110:399

    Article  Google Scholar 

  26. Vahabi M, Hadavandmirzaei H, Kamkari B, Safari H (2021) Interaction of a pair of in-line bubbles ascending in an Oldroyd-B liquid: a numerical study. Eur J Mech B/Fluids 85:413

    Article  MathSciNet  Google Scholar 

  27. Monaghan JJ, Kajtar JB (2009) SPH particle boundary forces for arbitrary boundaries. Comput Phys Commun 180:1811

    Article  MathSciNet  Google Scholar 

  28. Hirt CW, Nichols BD (1981) Volume of fluid (VOF) method for the dynamics of free boundaries. J Comput Phys 39:201

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, College of Engineering, Central Tehran Branch, Islamic Azad University, Tehran, Iran

    M. Vahabi

Authors
  1. M. Vahabi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Vahabi.

Additional information

Technical Editor: Edson Jose Soares.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vahabi, M. The effect of thixotropy on dam-break flow: a numerical study by smoothed particle hydrodynamics. J Braz. Soc. Mech. Sci. Eng. 43, 512 (2021). https://doi.org/10.1007/s40430-021-03241-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-021-03241-9

Keywords

Search

Navigation