Skip to main content
SpringerLink
Log in

Free vibration and wave propagation of axially moving functionally graded Timoshenko microbeams

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

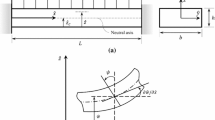
The transverse free vibration and wave propagation of functionally graded microbeams with an axial motion are investigated based on a nonlocal theory and the Timoshenko beam model. It is assumed the material properties of functionally graded microbeams vary along the thickness direction. The neutral plane of functionally graded materials is introduced, and the inhomogeneity of functionally graded Timoshenko microbeams is considered. The governing equations are derived using Hamilton’s principle, and the differential quadrature method is utilized to determine the first three-order natural frequencies of the microbeams with simply supported and clamped boundary conditions, respectively. The effects of gradient index, nonlocal parameter and axial velocity on natural frequencies are investigated. Moreover, the wave propagation characteristics of functionally graded Timoshenko microbeams are analyzed, and the significant influences of wave number and other variables on wave propagation frequencies and wave velocities are studied. The different influence patterns of nonlocal effect are observed in transverse vibration and wave propagation. The nonlocality shows a weakening phenomenon in transverse vibration of axially moving functionally graded Timoshenko microbeams, while it reveals both weakening and strengthening phenomena in wave propagation. Therefore, two kinds of existing nonlocal scale effects are further confirmed and this is an additional contribution of the present paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Cagin T, Che J, Gardos MN, Fijany A, Goddard WA III (1999) Simulation and experiments on friction and wear of diamond: a material for MEMS and NEMS application. Nanotechnology 10(3):278–284

    Google Scholar 

  2. Wang LF, Hu HY (2005) Flexural wave propagation in single-walled carbon nanotubes. Phys Rev B 71:195412

    Google Scholar 

  3. Chen WQ, Wu B, Zhang CL, Zhang Ch (2014) On wave propagation in anisotropic elastic cylinders at nanoscale: surface elasticity and its effect. Acta Mech 225(10):2743–2760

    MathSciNet  MATH  Google Scholar 

  4. Huang HW, Uslu FE, Katsamba P, Lauga E, Sakar MS, Nelson BJ (2019) Adaptive locomotion of artificial microswimmers. Sci Adv 5(1):eaau1532

    Google Scholar 

  5. Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54(9):4703–4710

    Google Scholar 

  6. Yang XD, Lim CW (2009) Nonlinear vibrations of nano-beams accounting for nonlocal effect using a multiple scale method. Sci China Technol Sci 52(3):617–621

    MATH  Google Scholar 

  7. Lim CW (2010) On the truth of nanoscale for nanobeams based on nonlocal elastic stress field theory: equilibrium, governing equation and static deflection. Appl Math Mech (English Edition) 31(1):37–54

    MathSciNet  MATH  Google Scholar 

  8. Wang L (2011) A modified nonlocal beam model for vibration and stability of nanotubes conveying fluid. Physica E 44:25–28

    Google Scholar 

  9. Ke LL, Wang YS, Wang ZD (2012) Nonlinear vibration of the piezoelectric nanobeams based on the nonlocal theory. Compos Struct 94(6):2038–2047

    Google Scholar 

  10. Bastami M, Behjat B (2018) Free vibration and buckling investigation of piezoelectric nano-plate in elastic medium considering nonlocal effects. J Braz Soc Mech Sci Eng 40(6):281

    Google Scholar 

  11. Shen JP, Wang PY, Li C, Wang YY (2019) New observations on transverse dynamics of microtubules based on nonlocal strain gradient theory. Compos Struct 225:111036

    Google Scholar 

  12. Wang CM, Zhang YY, He XQ (2007) Vibration of nonlocal Timoshenko beams. Nanotechnology 18(10):105401

    Google Scholar 

  13. Yan W, Lim CW, Cai JB, Chen WQ (2007) An electromechanical impedance approach for quantitative damage detection in Timoshenko beams with piezoelectric patches. Smart Mater Struct 16(4):1390–1400

    Google Scholar 

  14. Ke LL, Xiang Y, Yang J, Kitipornchai S (2009) Nonlinear free vibration of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory. Comput Mater Sci 47(2):409–417

    Google Scholar 

  15. Yang J, Ke LL, Kitipornchai S (2010) Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory. Physica E 42(5):1727–1735

    Google Scholar 

  16. Roque CMC, Ferreira AJM, Reddy JN (2011) Analysis of Timoshenko nanobeams with a nonlocal formulation and meshless method. Int J Eng Sci 49(9):976–984

    MATH  Google Scholar 

  17. Wang B, Deng ZC, Zhang K (2013) Nonlinear vibration of embedded single-walled carbon nanotube with geometrical imperfection under harmonic load based on nonlocal Timoshenko beam theory. Appl Math Mech (English Edition) 34(3):269–280

    MathSciNet  MATH  Google Scholar 

  18. Ansari R, Gholami R, Rouhi H (2015) Size-dependent nonlinear forced vibration analysis of magneto-electro-thermo-elastic Timoshenko nanobeams based upon the nonlocal elasticity theory. Compos Struct 126:216–226

    Google Scholar 

  19. Xu XJ, Deng ZC, Zhang K, Xu W (2016) Observations of the softening phenomena in the nonlocal cantilever beams. Compos Struct 145:43–57

    Google Scholar 

  20. Barretta R, Caporale A, Faghidian SA, Luciano R, de Sciarra FM, Medaglia CM (2019) A stress-driven local-nonlocal mixture model for Timoshenko nano-beams. Compos B Eng 164:590–598

    Google Scholar 

  21. Zhang K, Ge MH, Zhao C, Deng ZC, Xu XJ (2019) Free vibration of nonlocal Timoshenko beams made of functionally graded materials by Symplectic method. Compos B Eng 156:174–184

    Google Scholar 

  22. Sui SH, Chen L, Li C, Liu XP (2015) Transverse vibration of axially moving functionally graded materials based on Timoshenko beam theory. Math Probl Eng 2015:391452

    MathSciNet  MATH  Google Scholar 

  23. Nikkhoo A, Zolfaghari S, Kiani K (2017) A simplified-nonlocal model for transverse vibration of nanotubes acted upon by a moving nanoparticle. J Braz Soc Mech Sci Eng 39(12):4929–4941

    Google Scholar 

  24. Cao DQ, Tucker RW, Wang C (2003) A stochastic approach to cable dynamics with moving rivulets. J Sound Vib 268(2):291–304

    Google Scholar 

  25. Huang JL, Su RKL, Li WH, Chen SH (2011) Stability and bifurcation of an axially moving beam tuned to three-to-one internal resonances. J Sound Vib 330(3):471–485

    Google Scholar 

  26. Yang XD, Zhang W, Chen LQ, Yao MH (2012) Dynamical analysis of axially moving plate by finite difference method. Nonlinear Dyn 67(2):997–1006

    MathSciNet  MATH  Google Scholar 

  27. Yang XD, Zhang W (2014) Nonlinear dynamics of axially moving beam with coupled longitudinal–transversal vibrations. Nonlinear Dyn 78(4):2547–2556

    MathSciNet  Google Scholar 

  28. Ding H, Zhang Z, Chen LQ (2018) Vibration reduction effect of one-way clutch on belt-drive systems. Eur J Mech A Solids 71:378–385

    MathSciNet  MATH  Google Scholar 

  29. Ding H, Lim CW, Chen LQ (2018) Nonlinear vibration of a traveling belt with non-homogeneous boundaries. J Sound Vib 424:78–93

    Google Scholar 

  30. Kiani K (2013) Longitudinal, transverse, and torsional vibrations and stabilities of axially moving single-walled carbon nanotubes. Curr Appl Phys 13(8):1651–1660

    Google Scholar 

  31. Liu JJ, Li C, Fan XL, Tong LH (2017) Transverse free vibration and stability of axially moving nanoplates based on nonlocal elasticity theory. Appl Math Model 45:65–84

    MathSciNet  MATH  Google Scholar 

  32. Wang J, Shen H, Zhang B, Liu J, Zhang Y (2018) Complex modal analysis of transverse free vibrations for axially moving nanobeams based on the nonlocal strain gradient theory. Physica E 101:85–93

    Google Scholar 

  33. Şimsek M, Yurtcu HH (2013) Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Compos Struct 97:378–386

    Google Scholar 

  34. Barretta R, Feo L, Luciano R, de Sciarra FM (2016) Functionally graded Timoshenko nanobeams: a novel nonlocal gradient formulation. Compos B Eng 100:208–219

    Google Scholar 

  35. Zhang DG, Zhou YH (2009) A theoretical analysis of FGM thin plates based on physical neutral surface. Comput Mater Sci 44(2):716–720

    Google Scholar 

  36. Sun Y, Li SR, Romesh CB (2016) Thermal buckling and post-buckling of FGM Timoshenko beams on nonlinear elastic foundation. J Therm Stresses 39(1):11–26

    Google Scholar 

  37. Zeighampour H, Tadi BY (2015) Free vibration analysis of axially functionally graded nanobeam with radius varies along the length based on strain gradient theory. Appl Math Model 39(18):5354–5369

    MathSciNet  MATH  Google Scholar 

  38. Mousavi T, Bornassi S, Haddadpour H (2013) The effect of small scale on the pull-in instability of nano-switches using DQM. Int J Solids Struct 50(9):1193–1202

    Google Scholar 

  39. Li SR, Wan ZQ, Zhang JH (2014) Free vibration of functionally graded beams based on both classical and first-order shear deformation beam theories. Appl Math Mech (English Edition) 35(5):591–606

    MathSciNet  MATH  Google Scholar 

  40. Li C, Lai SK, Yang X (2019) On the nano-structural dependence of nonlocal dynamics and its relationship to the upper limit of nonlocal scale parameter. Appl Math Model 69:127–141

    MathSciNet  Google Scholar 

  41. Lim CW (2010) Is a nanorod (or nanotube) with a lower Young’s modulus stiffer? Is not Young’s modulus a stiffness indicator? Sci China Phys Mech Astron 53(4):712–724

    Google Scholar 

  42. Lim CW, Yang Q (2011) Nonlocal thermal-elasticity for nanobeam deformation: exact solutions with stiffness enhancement effects. J Appl Phys 110(1):013514

    Google Scholar 

  43. Li C, Li S, Yao LQ, Zhu ZK (2015) Nonlocal theoretical approaches and atomistic simulations for longitudinal free vibration of nanorods/nanotubes and verification of different nonlocal models. Appl Math Model 39(15):4570–4585

    MathSciNet  MATH  Google Scholar 

  44. Li C, Yao LQ, Chen WQ, Li S (2015) Comments on nonlocal effects in nano-cantilever beams. Int J Eng Sci 87:47–57

    Google Scholar 

  45. Shen JP, Li C (2017) A semi-continuum-based bending analysis for extreme-thin micro/nano-beams and new proposal for nonlocal differential constitution. Compos Struct 172:210–220

    Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Nos. 11572210, 11972240), the Postgraduate Research and Innovation Project of Jiangsu Province (No. KYCX17_1983) and the Open Project of State Key Laboratory of Mechanics and Control of Mechanical Structures (Nanjing University of Aeronautics and Astronautics) (Grant No. MCMS-0418G01).

Author information

Authors and Affiliations

  1. School of Rail Transportation, Soochow University, Suzhou, 215131, Jiangsu, China

    L. Q. Yao, C. J. Ji, J. P. Shen & C. Li

  2. State Key Laboratory of Mechanics and Control of Mechanical Structures and College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, Jiangsu, China

    C. Li

Authors
  1. L. Q. Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. C. J. Ji
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. P. Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. C. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to C. Li.

Additional information

Technical Editor: José Roberto de França Arruda.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yao, L.Q., Ji, C.J., Shen, J.P. et al. Free vibration and wave propagation of axially moving functionally graded Timoshenko microbeams. J Braz. Soc. Mech. Sci. Eng. 42, 137 (2020). https://doi.org/10.1007/s40430-020-2206-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-020-2206-9

Keywords

Search

Navigation