Skip to main content
SpringerLink
Log in

Dynamic analysis of a pipe conveying a two-phase fluid considering uncertainties in the flow parameters

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

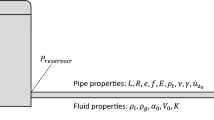
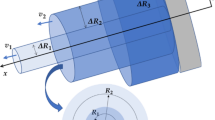
This paper is interested in the dynamics of a horizontal pipe conveying a two-phase fluid (gas and liquid), which is a problem of great regard for the oil and gas industry. The purpose of this paper is twofold. First, it introduces dimensionless coefficients that carry the information of the two-phase flow, allowing the dynamic equation to be written analogously to the equation of a single-phase fluid. Second, a probabilistic model is developed considering uncertainties in three flow parameters, (1) the flow profile factor, (2) the slip ratio and (3) the vapour quality, in order to analyse the influence of these parameters on the dynamic stability and on the frequency response of the system. The pipe is described using the linear elastic Euler–Bernoulli beam theory, and the fluid is modelled taking into account a constant tangential velocity of the flow. The coupled system is discretized by means of the finite element method, and the stochastic problem is approximated using the Monte Carlo method. The flow parameters affect greatly the system response, and different values of the critical flow velocity are obtained, depending on the level of uncertainty of the parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Ariaratnam ST, Namachchivaya NS (1986) Dynamic stability of pipes conveying fluid with stochastic flow velocity. Random Vibration Status Recent Dev 14:1–17

    MathSciNet  MATH  Google Scholar 

  2. Beltrao, R.L.C., Sombra, C.L., Lage, A.C.V., Netto, J.R.F., Henriques, C.C.D., et al. (2009) SS: pre-salt santos basin-challenges and new technologies for the development of the pre-salt cluster, Santos Basin, Brazil. In: Offshore technology conference

  3. Dalkilic A, Laohalertdecha S, Wongwises S (2008) Effect of void fraction models on the two-phase friction factor of r134a during condensation in vertical downward flow in a smooth tube. Int Commun Heat Mass Transf 35(8):921–927

    Article  Google Scholar 

  4. Drew DA (1983) Mathematical modeling of two-phase flow. Annu Rev Fluid Mech 15(1):261–291

    Article  Google Scholar 

  5. Ebrahimi-Mamaghani A, Sotudeh-Gharebagh R, Zarghami R, Mostoufi N (2019) Dynamics of two-phase flow in vertical pipes. J Fluids Struct 87:150–173

    Article  Google Scholar 

  6. Energy: Guidelines for the Avoidance of Vibration Induced Fatigue in Process Pipework. Energy Institute (Great Britain) and Energy Institute (Great Britain) Staff (2008)

  7. Ghayesh MH, Païdoussis MP, Amabili M (2013) Nonlinear dynamics of cantilevered extensible pipes conveying fluid. J Sound Vib 332(24):6405–6418

    Article  Google Scholar 

  8. Guo, C., Zhang, C., Païdoussis, M. (2013) Modification of equation of motion of fluid-conveying pipe for laminar and turbulent flow profiles. In: Seismic safety evaluation of concrete dams. Elsevier, pp 221–237

  9. Guo Y, Zhu B, Zhao X, Chen B, Li Y (2020) Dynamic characteristics and stability of pipe-in-pipe system conveying two-phase flow in thermal environment. Appl Ocean Res 103:102333

    Article  Google Scholar 

  10. Ibrahim R (2010) Overview of mechanics of pipes conveying fluids: part I: fundamental studies. J Pressure Vessel Technol 132(3):034001

    Article  MathSciNet  Google Scholar 

  11. Jayenes ET (2003) Probability theory: the logic science. Cambridge University Press, Cambridge

    Book  Google Scholar 

  12. Lacarbonara W (2013) Nonlinear structural mechanics: theory, dynamical phenomena and modeling. Springer, Berlin

    Book  Google Scholar 

  13. Liu G, Wang Y (2018) Study on the natural frequencies of pipes conveying gas-liquid two-phase slug flow. Int J Mech Sci 141:168–188

    Article  Google Scholar 

  14. Mehta M (1991) Random matrices. Academic Press, Cambridge

    MATH  Google Scholar 

  15. Meirovitch L (2010) Fundamentals of vibrations. Waveland Press, Long Grove

    Google Scholar 

  16. Modarres-Sadeghi Y, Païdoussis M (2009) Nonlinear dynamics of extensible fluid-conveying pipes, supported at both ends. J Fluids Struct 25(3):535–543

    Article  Google Scholar 

  17. Monette C, Pettigrew M (2004) Fluidelastic instability of flexible tubes subjected to two-phase internal flow. J Fluids Struct 19(7):943–956

    Article  Google Scholar 

  18. Nakamura T, Kaneko S, Inada F, Kato M, Ishihara K, Nishihara T, Mureithi NW, Langthjem MA (2013) Flow-induced vibrations: classifications and lessons from practical experiences. Butterworth-Heinemann, Oxford

    Google Scholar 

  19. Paidoussis M, Moon F (1988) Nonlinear and chaotic fluidelastic vibrations of a flexible pipe conveying fluid. J Fluids Struct 2(6):567–591

    Article  Google Scholar 

  20. Paidoussis MP (1998) Fluid-structure interactions: slender structures and axial flow, vol 1. Academic Press, Cambridge

    Google Scholar 

  21. Paidoussis MP, Issid N (1974) Dynamic stability of pipes conveying fluid. J Sound Vib 33(3):267–294

    Article  Google Scholar 

  22. Papathanassiou G, Maeder P, DiPippo R, Dickinson D (1983) Void fraction correlations in two-phase horizontal flow. New Mexico, Los Alamos National Laboratory (LANL)

    Book  Google Scholar 

  23. Rahmati M, Mirdamadi HR, Goli S (2018) Divergence instability of pipes conveying fluid with uncertain flow velocity. Physica A 491:650–665

    Article  MathSciNet  Google Scholar 

  24. Rice C (1987) The effect of void fraction correlation and heat flux assumption on refrigerant charge inventory predictions. ASHRAE Trans 93(1):341–367

    Google Scholar 

  25. Ritto T, Soize C, Rochinha F, Sampaio R (2014) Dynamic stability of a pipe conveying fluid with an uncertain computational model. J Fluids Struct 49:412–426

    Article  Google Scholar 

  26. Riverin JL, Pettigrew M (2007) Vibration excitation forces due to two-phase flow in piping elements. J Pressure Vessel Technol 129(1):7–13

    Article  Google Scholar 

  27. Sazesh S, Shams S (2019) Vibration analysis of cantilever pipe conveying fluid under distributed random excitation. J Fluids Struct 87:84–101

    Article  Google Scholar 

  28. Shah S, Mignolet MP (2019) Effects of structural-fluid coupling uncertainty on the dynamic behavior of nominally straight and uniform pipes conveying fluid: Modeling and numerical study. J Fluids Struct 85:55–76

    Article  Google Scholar 

  29. Soize C (2000) Nonparametric model of random uncertainties for reduced matrix models in structural dynamics. Probab Eng Mech 14:277–294

    Article  Google Scholar 

  30. Wachel J (1995) Displacement method for determining acceptable piping vibration amplitudes. ASME-PUBLICATIONS-PVP 313:197–208

    Google Scholar 

  31. Wachel, J., Morton, S.J., Atkins, K.E., et al.: Piping vibration analysis. In: Proceedings of the 19th turbomachinery symposium. Texas A&M University. Turbomachinery Laboratories (1990)

  32. Woldesemayat MA, Ghajar AJ (2007) Comparison of void fraction correlations for different flow patterns in horizontal and upward inclined pipes. Int J Multiph Flow 33(4):347–370

    Article  Google Scholar 

Download references

Acknowledgements

T.G. Ritto would like to acknowledge that this investigation was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) - Finance code 001 - Grant PROEX 803/2018, and the Brazilian agencies: Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPQ) - Grants 303768/2018-5, Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) - Grant E-26/203.187/2017.

Author information

Authors and Affiliations

  1. PETROBRAS - Petróleo Brasileiro S.A., Av. Henrique Valadares 28, Centro, Rio de Janeiro, RJ, 20231-030, Brazil

    P. J. V. Ponte

  2. Department of Mechanical Engineering, Universidade Federal do Rio de Janeiro, Rua Moniz Aragão 360, Cidade Universitária, Rio de Janeiro, RJ, 21941-594, Brazil

    T. G. Ritto

  3. Laboratoire de Mécanique des Structures et des Systèmes Couplés (LMSSC) - CNAM, 292 Rue Saint-Martin, 75003, Paris, France

    J.-F. Deü

Authors
  1. P. J. V. Ponte
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. G. Ritto
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J.-F. Deü
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. J. V. Ponte.

Additional information

Technical Editor: Andre T. Beck, Dr.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ponte, P.J.V., Ritto, T.G. & Deü, JF. Dynamic analysis of a pipe conveying a two-phase fluid considering uncertainties in the flow parameters. J Braz. Soc. Mech. Sci. Eng. 42, 626 (2020). https://doi.org/10.1007/s40430-020-02710-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-020-02710-x

Keywords

Search

Navigation