Skip to main content
SpringerLink
Log in

Behavior of stratifications and convective phenomena in mixed convection flow of 3D Carreau nanofluid with radiative heat flux

  • Review
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

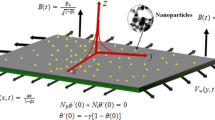
Nanoliquids, the engineered liquids with isolated effectual nanoparticles have disclosed a surprising thermo-physical effects and added functionalities and therefore have supported an extensive sort of essential applications. In particular, nanoliquids have displayed pointedly improved aptitude of heat transfer as equated to traditional functioning liquids. The notable intention of current scrutiny is to explore the features of combined convective and stratification phenomena by utilizing Brownian and thermophoresis nanoparticles on 3D mixed convection flow of magnetite Carreau fluid influenced by a bidirectional stretching surface. The heat transport phenomenon is also betrothed in the manifestation of thermal radiation and the heat sink/source. By means of suitable conversions the nonlinear PDEs transformed into nonlinear ODEs. To identify the behavior of numerous somatic parameters, numerically bvp4c tactic has been worked to elucidate the governing ODEs. The graphical depiction is delineated and tables are organized for diverse physical parameters on Carreau nanofluid. It is scrutinized that the impact of magnetic parameter on both the velocity components is analogous and diminishes both the velocities for shear thinning/thickening liquids. Moreover, the present exploration reports that the mixed convection and thermal stratification parameters decline the liquid temperature and allied thickness of the thermal boundary layer for both shear thickening/thinning liquids.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

\({\mathbf{S}}^{ * }\) :

Cauchy stress tensor

p :

Pressure

I :

Identity tensor

\(\dot{\gamma }\) :

Shear rate

\(\varGamma\) :

Material rate constant

\((\mu_{0} ,\mu_{\infty } )\) :

Zero and infinity shear rate viscosities

\({\mathbf{A}}_{1}\) :

First Rivlin–Ericksen tensor

n :

Power law index

u, v, w :

Velocity components

x, y, z :

Space coordinates

\(\nu\) :

Kinematic viscosity

\(\sigma\) :

Electrical conductivity

\(\rho_{{f}}\) :

Fluid density

B 0 :

Strength of magnetic field

g :

Gravitational acceleration

\(\alpha_{1}\) :

Thermal diffusivity

k :

Nanofluid thermal conductivity

\(\left( {\beta_{{T}} ,\beta_{{C}} } \right)\) :

Thermal and concentration coefficients expansion

(T, C):

Temperature and concentration of fluid

\(\tau\) :

Effective heat capacity ratio

D B :

Brownian diffusion coefficient

D T :

Thermophoresis diffusion coefficient

\((T_{\infty } ,C_{\infty } )\) :

Nanofluid ambient temperature and concentration

\((T_{0} ,C_{0} )\) :

Reference temperature and concentration

\((d,d_{1} ,e,e_{1} )\) :

Dimensionless constants

q r :

Radiative heat flux

k * :

Mean absorption coefficient

\(\sigma^{ * }\) :

Stefan–Boltzmann constant

Q 0 :

Heat source/sink coefficient

\(U_{w} (x),\;V_{w} (x)\) :

Stretching velocities

a, b :

Positive constants

\(\left( {h_{{f}} ,h_{{m}} } \right)\) :

Heat and mass wall transfer coefficient

\(\left( {T_{{f}} ,C_{{f}} } \right)\) :

Heated fluid temperature and concentration

\(\eta\) :

Dimensionless variable

(We 1, We 2):

Local Weissenberg numbers

M :

Magnetic parameter

\(\lambda^{*}\) :

Mixed convection parameter

N*:

Buoyancy ratio parameter

R :

Thermal radiation

(S 1, S 2):

Thermal and mass stratification parameters

\((\gamma_{1} ,\gamma_{2} )\) :

Thermal and mass Biot numbers

N b :

Brownian motion parameter

N t :

Thermophoresis parameter

\(\delta\) :

Heat source/sink parameter

Le :

Lewis number

α :

Ratio of stretching rates parameter

\((\tau_{{xz}} ,\tau_{{yz}} )\) :

Surface shear stresses along x- and y-directions

\((C_{{fx}} ,C_{{fy}} )\) :

Skin friction coefficients

\(\left( {Nu_{x} ,Sh_{x} } \right)\) :

Local Nusselt and Sherwood numbers

\(Re_{x}\) :

Local Reynolds number

(f, g):

Dimensionless velocities

\(\theta\) :

Dimensionless temperature

\(\varphi\) :

Dimensionless concentration

ODEs:

Ordinary differential equations

PDEs:

Partial differential equations

3D:

Three dimensional

References

  1. Choi SUS (1995) Enhancing thermal conductivity of fluids with nanoparticles. ASME Int Mech Eng 66:99–105

    Google Scholar 

  2. Mahanthesh B, Gireesha BJ, Gorla RSR, Abbasi FM, Shehzad SA (2016) Numerical solutions for magnetohydrodynamic flow of nanofluid over a bidirectional non-linear stretching surface with prescribed surface heat flux boundary. J Magn Magn Mater 417:189–196

    Article  Google Scholar 

  3. Hayat T, Rashid M, Imtiaz M, Alsaedi A (2017) MHD convective flow due to a curved surface with thermal radiation and chemical reaction. J Mol Liq 225:482–489

    Article  Google Scholar 

  4. Khan M, Irfan M, Khan WA (2017) Numerical assessment of solar energy aspects on 3D magneto-Carreau nanofluid: a revised proposed relation. Int J Hydrog Energy 42:22054–22065

    Article  Google Scholar 

  5. Hayat T, Khan MI, Waqas M, Alsaedi A, Khan MI (2017) Radiative flow of micropolar nanofluid accounting thermophoresis and Brownian moment. Int J Hydrog Energy 42:16821–16833

    Article  Google Scholar 

  6. Upadhya SM, Raju CSK (2017) Multiple slips on magnetohydrodynamic Carreau dustynano fluid over a stretched surface with Cattaneo–Christov heat flux. J Nanofluids 1:1074–1108

    Article  Google Scholar 

  7. Mahanthesh B, Mabood F, Gireesha BJ, Gorla RSR (2017) Effects of chemical reaction and partial slip on the three-dimensional flow of a nanofluid impinging on an exponentially stretching surface. Eur Phys J Plus. https://doi.org/10.1140/epjp/i2017-11389-8

    Article  Google Scholar 

  8. Mahanthesh B, Gireesha BJ, Raju CSK (2017) Cattaneo–Christov heat flux on UCM nanofluid flow across a melting surface with double stratification and exponential space dependent internal heat source. Inf Med Unlocked 9:26–34

    Article  Google Scholar 

  9. Anwar MS, Rasheed A (2017) Simulations of a fractional rate type nanofluid flow with non-integer Caputo time derivatives. Comput Math Appl 74:2485–2502

    Article  MathSciNet  Google Scholar 

  10. Raju CSK, Sandeep N (2017) Unsteady Casson nanofluid flow over a rotating cone in a rotating frame filled with ferrous nanoparticles: a numerical study. J. Magn Magn Mater 421:216–224

    Article  Google Scholar 

  11. Mustafa M, Khan JA, Hayat T, Alsaedi A (2017) Buoyancy effects on the MHD nanofluid flow past a vertical surface with chemical reaction and activation energy. Int J Heat Mass Transf 108:1340–1346

    Article  Google Scholar 

  12. Haq RU, Rashid I, Khan ZA (2017) Effects of aligned magnetic field and CNTs in two different base fluids over a moving slip surface. J Mol Liq 243:682–688

    Article  Google Scholar 

  13. Hayat T, Khan MI, Waqas M, Alsaedi A, Farooq M (2017) Numerical simulation for melting heat transfer and radiation effects in stagnation point flow of carbon–water nanofluid. Comput Methods Appl Mech Eng 315:1011–1024

    Article  MathSciNet  Google Scholar 

  14. Irfan M, Khan M, Khan WA (2017) Numerical analysis of unsteady 3D flow of Carreau nanofluid with variable thermal conductivity and heat source/sink. Results Phys 7:3315–3324

    Article  Google Scholar 

  15. Raju CSK, Hoque MM, Anika NN, Mamatha SU, Sharma P (2017) Natural convective heat transfer analysis of MHD unsteady Carreau nanofluid over a cone packed with alloy nanoparticles. Powder Tech 317:408–416

    Article  Google Scholar 

  16. Hayat T, Rashid M, Alsaedi A, Ahmad B (2018) Flow of nanofluid by nonlinear stretching velocity. Results Phys 8:1104–1109

    Article  Google Scholar 

  17. Zeeshan A, Shezhad N, Ellahi R (2018) Analysis of activation energy in Couette–Poiseuille flow of nanofluid in the presence of chemical reaction and convective boundary conditions. Results Phys 8:502–512

    Article  Google Scholar 

  18. Upadhya SM, Raju CSK (2018) Comparative study of Eyring and Carreau fluids in a suspension of dust and nickel nanoparticles with variable conductivity. Eur Phys J Plus. https://doi.org/10.1140/epjp/i2018-11979-x

    Article  Google Scholar 

  19. Mukhopadhyay S, Ishak A (2012) Mixed convection flow along a stretching cylinder in a thermally stratified medium. J Appl Math https://doi.org/10.1155/2012/491695

    Article  MathSciNet  Google Scholar 

  20. Mahanthesh B, Gireesha BJ, Gorla RSR (2016) Heat and mass transfer effects on the mixed convective flow of chemically reacting nanofluid past a moving/stationary vertical plate. Alex Eng J 55:569–581

    Article  Google Scholar 

  21. Imtiaz M, Hayat T, Alsaedi A (2016) Mixed convection flow of Casson nanofluid over a stretching cylinder with convective boundary conditions. Adv Powder Tech 27:2245–2256

    Article  Google Scholar 

  22. Waqas M, Khan MI, Hayat T, Alsaedi A (2017) Stratified flow of an Oldroyd-B nanoliquid with heat generation. Results Phys 7:2489–2496

    Article  Google Scholar 

  23. Besthapu P, Haq RU, Bandari S, Al-Mdallal QM (2017) Mixed convection flow of thermally stratified MHD nanofluid over an exponentially stretching surface with viscous dissipation effect. J Taiwan Inst Chem Eng 71:307–314

    Article  Google Scholar 

  24. Ibrahim SM, Lorenzini G, Kumar PV, Raju CSK (2017) Influence of chemical reaction and heat source on dissipative MHD mixed convection flow of a Casson nanofluid over a nonlinear permeable stretching sheet. Int J Heat Mass Transf 111:346–355

    Article  Google Scholar 

  25. Khan MI, Waqas M, Hayat T, Khan MI, Alsaedi A (2017) Behavior of stratification phenomenon in flow of Maxwell nanomaterial with motile gyrotactic microorganisms in the presence of magnetic field. Int J Mech Sci 131–132:426–434

    Article  Google Scholar 

  26. Hashim, Hamid A, Khan M (2018) Unsteady mixed convective flow of Williamson nanofluid with heat transfer in the presence of variable thermal conductivity and magnetic field. J Mol Liq 260:436–446

    Article  Google Scholar 

  27. Waqas M, Farooq M, Khan MI, Alsaedi A, Hayat T, Yasmeen T (2016) Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int J Heat Mass Transf 102:766–772

    Article  Google Scholar 

  28. Mamatha SU, Raju CSK, Makinde OD (2017) Effect of convective boundary condition on MHD Carreau dusty fluid over a stretching sheet with heat source. Defect Diffus Forum 377:233–241

    Article  Google Scholar 

  29. Mahanthesh B, Gireesha BJ, Athira PR (2017) Radiated flow of chemically reacting nanoliquid with an induced magnetic field across a permeable vertical plate. Results Phys 7:2375–2383

    Article  Google Scholar 

  30. Hayat T, Rafique K, Muhammad T, Alsaedi A (2018) Carbon nanotubes significance in Darcy–Forchheimer flow. Results Phys 8:26–33

    Article  Google Scholar 

  31. Hayat T, Rashid M, Alsaedi A (2018) Three dimensional radiative flow of magnetite-nanofluid with homogeneous-heterogeneous reactions. Results Phys 8:268–275

    Article  Google Scholar 

  32. Irfan M, Khan M, Khan WA, Ayaz M (2018) Modern development on the features of magnetic field and heat sink/source in Maxwell nanofluid subject to convective heat transport. Phys Lett A 382:1992–2002

    Article  Google Scholar 

  33. Upadhya SM, Raju CSK, Saleem S (2018) Nonlinear unsteady convection on micro and nanofluids with Cattaneo–Christov heat flux. Results Phys 9:779–786

    Article  Google Scholar 

  34. Irfan M, Khan M, Khan WA (2018) Interaction between chemical species and generalized Fourier’s law on 3D flow of Carreau fluid with variable thermal conductivity and heat sink/source: a numerical approach. Results Phys 10:107–117

    Article  Google Scholar 

  35. Carreau PJ (1972) Rheological equations from molecular network theories. Trans Soc Rheol 16:99–127

    Article  Google Scholar 

  36. Gireesha BJ, Kumar PBS, Mahanthesh B, Shehzad SA, Rauf A (2017) Nonlinear 3D flow of Casson–Carreau fluids with homogeneous–heterogeneous reactions: a comparative study. Results Phys 7:2762–2770

    Article  Google Scholar 

  37. Khan M, Irfan M, Khan WA, Alshomrani AS (2017) A new modeling for 3D Carreau fluid flow considering nonlinear thermal radiation. Results Phys 7:2692–2704

    Article  Google Scholar 

  38. Upadhya SM, Raju CSK (2018) Unsteady flow of Carreau fluid in a suspension of dust and graphene nanoparticles with Cattaneo–Christov heat flux. J Heat Transf. https://doi.org/10.1115/1.4039904

    Article  Google Scholar 

  39. Wang CY (1984) The three dimensional flow due to a stretching flat surface. Phys Fluids 27:1915–1917

    Article  MathSciNet  Google Scholar 

  40. Liu IC, Anderson HI (2008) Heat transfer over a bidirectional stretching sheet with variable thermal conditions. Int J Heat Mass Transf 51:4018–4024

    Article  Google Scholar 

  41. Khan M, Irfan M, Khan WA (2017) Impact of forced convective radiative heat and mass transfer mechanisms on 3D Carreau nanofluid: a numerical study. Eur Phys J Plus. https://doi.org/10.1140/epjp/i2017-11803-3

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Quaid-i-Azam University, Islamabad, 44000, Pakistan

    M. Irfan & M. Khan

  2. Department of Mathematics and Statistics, Hazara University, Mansehra, 21300, Pakistan

    W. A. Khan

Authors
  1. M. Irfan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. W. A. Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Irfan.

Additional information

Technical Editor: Cezar Negrao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Irfan, M., Khan, M. & Khan, W.A. Behavior of stratifications and convective phenomena in mixed convection flow of 3D Carreau nanofluid with radiative heat flux. J Braz. Soc. Mech. Sci. Eng. 40, 521 (2018). https://doi.org/10.1007/s40430-018-1429-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1429-5

Keywords

Search

Navigation