Skip to main content
SpringerLink
Log in

Effectiveness of magnetic field on the flow of Jeffrey fluid in an annulus with rotating concentric cylinders

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

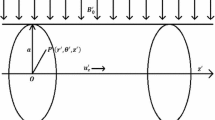
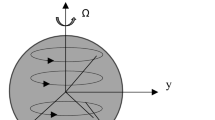
In the present article, the flow of an incompressible Jeffrey fluid in the annulus of rotating concentric cylinders in the presence of magnetic field has been investigated. The governing equations for Jeffrey fluid model are formulated considering cylindrical coordinates system. The constitutive equations for the fluid flow have been simplified under the choice of velocity. The existence of the solution to the momentum equation is established using Schauder’s fixed point theorem. The analytical solutions for the velocity and skin friction coefficient are presented using modified Bessel functions. The effect of various parameters of interest such as the rotating speed of the cylinders, magnetic field parameter, non-Newtonian fluid parameter and the aspect ratio of cylinders on the velocity field and skin friction coefficient have been studied. It is observed that, the velocity decreases with increase in magnetic field parameter and aspect ratio of the cylinders. It is also depicted that, the higher velocities are seen in Newtonian fluid model as compared to the Jeffrey fluid model. The results obtained for the flow characteristics reveal many interesting behaviors that warrant further study of the effects of rotation on the flow characteristics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Abbreviations

\({\mu }\) :

Viscosity coefficient

p :

Pressure

t :

Time

\({r_1}\) :

Radius of inner cylinder

\({r_2}\) :

Radius of outer cylinder

I :

Identity vector

\({B_0}\) :

Strength of the magnetic field

\({\lambda _1}\) :

Ratio of relaxation and retardation times

\({\lambda _2}\) :

Retardation time

\({\Omega _1,\Omega _2}\) :

Angular velocities

\({\sigma }\) :

Electrical conductivity of the fluid

v :

Velocity field

\({B_1}\) :

Dimensionless magnetic field parameter

\({\omega }\) :

Dimensionless rotation parameter

\({W_B}\) :

Energy of the magnetic field in a cross section

\({m_0}\) :

Mass of the fluid element

H :

Magnetic field intensity

\({C_{{\mathrm{f}}}}\) :

Skin friction coefficient

\({\varvec{\tau }}\) :

Cauchy stress tensor

\({\varvec{q}}\) :

Velocity vector

\({\dot{\varvec{D}}}\) :

Deformation tensor

\({\ddot{\varvec{D}}}\) :

Material derivative

\({{\mathbf{J}}}\) :

Electric current density

\({{\mathbf{B}}}\) :

Total magnetic field

References

  1. Hayat T, Khan M, Ayub M (2004) On the explicit analytic solutions of an Oldroyd 6-constant fluid. Int J Eng Sci 42:123–135

    Article  MathSciNet  Google Scholar 

  2. Fetecau C, Fetecau C (2005) On some axial Couette flows of non-Newtonian fluids. Z Angrew Math Phys 56(6):1098–1106

    Article  MathSciNet  Google Scholar 

  3. Tan W, Takashi M (2005) Stokes first problem for second grade fluid in a porous half space with heated boundary. Int J Nonlinear Mech 40(4):515–522

    Article  Google Scholar 

  4. Tan W, Takashi M (2005) Stokes first problem for an Oldroyd-B fluid in a porous half space. Phys Fluids 17(2):023101

    Article  MathSciNet  Google Scholar 

  5. Hayat T, Abbas Z, Sajid M (2006) Series solution for the upper-convected Maxwell fluid over a porous stretching plate. Phys Lett A 358(5–6):396–403

    Article  Google Scholar 

  6. Bhatti MM, Zeeshan A, Ijaz N (2016) Slip effects and endoscopy analysis on blood flow of particle-fluid suspension induced by peristaltic wave. J Mol Liq 218:240–245

    Article  Google Scholar 

  7. Bhatti MM, Zeeshan A, Ellahi R (2016) Heat transfer analysis on peristaltically induced motion of particle-fluid suspension with variable viscosity: clot blood model. Comput Methods Prog Bio 137:115–124

    Article  Google Scholar 

  8. Nadeem S, Muhammad N (2016) Impact of stratification and Cattaneo–Christov heat flux in the flow saturated with porous medium. J Mol Liq 224:423–430

    Article  Google Scholar 

  9. Bhatti MM, Zeeshan A (2016) Heat and mass transfer analysis on peristaltic flow of particle-fluid suspension with slip effects. J Mech Med Biol 17(02):1750028. https://doi.org/10.1142/S0219519417500282

    Article  Google Scholar 

  10. Muhammad N, Nadeem S, Mustafa T (2017) Squeezed flow of a nanofluid with Cattaneo–Christov heat and mass fluxes. Results Phys 7:862–869

    Article  Google Scholar 

  11. Nadeem S, Ahmad S, Muhammad N, Mustafa MT (2017) Chemically reactive species in the flow of a Maxwell fluid. Results Phys 7:2607–2613

    Article  Google Scholar 

  12. Nadeem S, Ahmad S, Muhammad N (2017) Cattaneo–Christov flux in the flow of a viscoelastic fluid in the presence of Newtonian heating. J Mol Liq 237:180–184

    Article  Google Scholar 

  13. Pandey SK, Tripathi D (2010) Unsteady model of transportation of Jeffrey-fluid by peristalsis. Int J Biomath 3(4):473–491

    Article  MathSciNet  Google Scholar 

  14. Srinivas S, Muthuraj R (2010) Peristaltic transport of a Jeffrey fluid under the effect of slip in an inclined asymmetric channel. Int J Appl Mech 2(2):437–455

    Article  Google Scholar 

  15. Bhatti MM, Zeeshan A (2016) Analytic study of heat transfer with variable viscosity on solid particle motion in dusty Jeffery fluid. Mod Phys Lett B 30(16):1650196

    Article  MathSciNet  Google Scholar 

  16. Ellahi R, Rahman SU, Nadeem S (2014) Blood flow of Jeffrey fluid in a catherized tapered artery with the suspension of nanoparticles. Phys Lett A 378(40):2973–2980

    Article  Google Scholar 

  17. Hayat T, Asad S, Alsaedi A (2015) Analysis for flow of Jeffrey fluid with nanoparticles. Chin Phys B 24(4):044702

    Article  Google Scholar 

  18. Rahman SU, Ellahi R, Nadeem S, Zia QMZ (2016) Simultaneous effects of nanoparticles and slip on Jeffrey fluid through tapered artery with mild stenosis. J Mol Liq 218:484–493

    Article  Google Scholar 

  19. Maqbool K, Shaheen S, Mann AB (2016) Exact solution of cilia induced flow of a Jeffrey fluid in an inclined tube. SpringerPlus 5:1379

    Article  Google Scholar 

  20. Hayat T, Qayyum S, Imtiaz M, Alsaedi A (2016) Three-dimensional rotating flow of Jeffrey fluid for Cattaneo–Christov heat flux model. AIP Adv 6(2):025012

    Article  Google Scholar 

  21. Hayat T, Khan M, Ayub M (2004) Couette and Poiseuille flows of an Oldroyd 6-constant fluid with magnetic field. J Math Anal Appl 298(1):225–244

    Article  MathSciNet  Google Scholar 

  22. Hayat T, Ali N (2008) Peristaltic motion of a Jeffrey fluid under the effect of a magnetic field in a tube. Commun Nonlinear Sci 13(7):1343–1352

    Article  MathSciNet  Google Scholar 

  23. Farooq M, Gull N, Alsaedi A, Hayat T (2015) MHD flow of a Jeffrey fluid with Newtonian heating. J Mech 31(3):319–329

    Article  Google Scholar 

  24. Narayana PVS, Babu DH (2016) Numerical study of MHD heat and mass transfer of a Jeffrey fluid over a stretching sheet with chemical reaction and thermal radiation. J Taiwan Inst Chem Eng 59:1825

    Google Scholar 

  25. Hayat T, Rafiq M, Ahmad B (2016) Soret and Dufour effects on MHD peristaltic flow of Jeffrey fluid in a rotating system with porous medium. PLoS ONE 11(1):e0145525

    Article  Google Scholar 

  26. Imtiaz M, Hayat T, Alsaedi A (2016) MHD convective flow of Jeffrey fluid due to a curved stretching surface with homogeneous–heterogeneous reactions. PLoS ONE 11(9):e0161641

    Article  Google Scholar 

  27. Khan AA, Muhammad S, Ellahi R, Zia QMZ (2016) Bionic study of variable viscosity on MHD peristaltic flow of Pseudoplastic fluid in an asymmetric channel. J Magn 21(2):273–280

    Article  Google Scholar 

  28. Ellahi R, Shivanian E, Abbasbandy S, Hayat T (2016) Numerical study of magnetohydrodynamics generalized Couette flow of Eyring–Powell fluid with heat transfer and slip condition. Int J Numer Method Heat Fluid Flow 26(5):1433–1445

    Article  MathSciNet  Google Scholar 

  29. Bhatti MM, Ellahi R, Zeeshan A (2016) Study of variable magnetic field on the peristaltic flow of Jeffrey fluid in a non-uniform rectangular duct having compliant walls. J Mol Liq 222:101–108

    Article  Google Scholar 

  30. Bhatti MM, Zeeshan A, Ellahi R (2016) Study of heat transfer with nonlinear thermal radiation on sinusoidal motion of magnetic solid particles in a dusty fluid. J Theor Appl Mech 46(3):75–94

    Article  MathSciNet  Google Scholar 

  31. Bhatti MM, Zeeshan A, Ellahi R (2016) Endoscope analysis on peristaltic blood flow of sisko fluid with titanium magneto-nanoparticles. Comput Biol Med 78:29–41

    Article  Google Scholar 

  32. Sheikholeslami M, Zia QMZ, Ellahi R (2016) Influence of induced magnetic field on free convection of nanofluid considering Koo–Kleinstreuer (KKL) correlation. Appl Sci 6(324):1–11. https://doi.org/10.3390/app6110324

    Article  Google Scholar 

  33. Khan AA, Usman H, Vafai K, Ellahi R (2016) Study of peristaltic flow of magnetohydrodynamic Walter’s B fluid with slip and heat transfer. Sci Iran 23(6):2650–2662

    Google Scholar 

  34. Bhatti MM, Zeeshan A, Ijaz I, Ellahi R (2017) Heat transfer and inclined magnetic field analysis on peristaltically induced motion of small particles. J Braz Soc Mech Sci Eng 39(9):3259–3267

    Article  Google Scholar 

  35. Ellahi R, Tariq MH, Hassan M, Vafai K (2017) On boundary layer magnetic flow of nano-Ferroliquid under the influence of low oscillating over stretchable rotating disk. J Mol Liq 229:339–345

    Article  Google Scholar 

  36. Bhatti MM, Zeeshan A, Ellahi R, Ijaz N (2017) Heat and mass transfer of two-phase flow with Electric double layer effects induced due to peristaltic propulsion in the presence of transverse magnetic field. J Mol Liq 230:237–246

    Article  Google Scholar 

  37. Hassan M, Zeeshan A, Majeed A, Ellahi R (2017) Particle shape effects on ferrofluids flow and heat transfer under influence of low oscillating magnetic field. J Magn Magn Mater 443:36–44

    Article  Google Scholar 

  38. Muhammad N, Nadeem S, Haq RU (2017) Heat transport phenomenon in the ferromagnetic fluid over a stretching sheet with thermal stratification. Results Phys 7:854–861

    Article  Google Scholar 

  39. Muhammad N, Nadeem S (2017) Ferrite nanoparticles Ni–ZnFe2O4, Mn–ZnFe2O4 and Fe2O4 in the flow of ferromagnetic nanofluid. Eur Phys J Plus 132(9):377

    Article  Google Scholar 

  40. Nadeem S, Raishad I, Muhammad N, Mustafa MT (2017) Mathematical analysis of ferromagnetic fluid embedded in a porous medium. Results Phys 7:2361–2368

    Article  Google Scholar 

  41. Ellahi R, Bhatti MM, Khalique CM (2017) Three-dimensional flow analysis of Carreau fluid model induced by peristaltic wave in the presence of magnetic field. J Mol Liq 241:1059–1068

    Article  Google Scholar 

  42. Bhatti MM, Zeeshan A, Ellahi R (2017) Simultaneous effects of coagulation and variable magnetic field on peristaltically induced motion of Jeffrey nanofluid containing gyrotactic microorganism. Microvasc Res 110:32–42

    Article  Google Scholar 

  43. Ijaz N, Zeeshan A, Bhatti MM, Ellahi R (2017) Analytical study on liquid-solid particles interaction in the presence of heat and mass transfer through a wavy channel. J Mol Liq 250:80–87

    Article  Google Scholar 

  44. Muhammad N, Nadeem S, Mustafa MT (2018) Analysis of ferrite nanoparticles in the flow of ferromagnetic nanofluid. PLoS ONE 13(1):e0188460

    Article  Google Scholar 

  45. Akbar NS, Nadeem S, Lee C (2013) Characteristics of Jeffrey fluid model for peristaltic flow of chyme in small intestine with magnetic field. Results Phys 3:152–160

    Article  Google Scholar 

  46. Ellahi R, Riaz A, Nadeem S, Mushtaq M (2013) Series solutions of magnetohydrodynamic peristaltic flow of a Jeffrey fluid in eccentric cylinders. Appl Math Inf Sci 7(4):1441–1449

    Article  Google Scholar 

  47. Yeadon WH, Yeadon AW (2001) Handbook of small electric motors. McGraw-Hill Education, Berlin

    MATH  Google Scholar 

  48. Riaz A, Razaq A, Awan AU (2017) Magnetic field and permeability effects on Jeffrey fluid in eccentric tubes having flexible porous boundaries. J Magn 22(4):642–648

    Article  Google Scholar 

  49. Vajravelu K, Cannon JR, Rollins D, Leto J (2002) On solutions of some non-linear differential equations arising in third grade fluids flows. Int J Eng Sci 40:1791–1805

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Lovely Professional University, Jalandhar, 144411, India

    Deepak Kumar & K. Ramesh

  2. Department of Mathematics, IKG Punjab Technical University, Kapurthala, 144603, India

    Deepak Kumar

  3. School of Mathematics, Thapar University, Patiala, 147004, India

    Sumit Chandok

Authors
  1. Deepak Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. Ramesh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sumit Chandok
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to K. Ramesh.

Additional information

Technical Editor: Cezar Negrao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, D., Ramesh, K. & Chandok, S. Effectiveness of magnetic field on the flow of Jeffrey fluid in an annulus with rotating concentric cylinders. J Braz. Soc. Mech. Sci. Eng. 40, 305 (2018). https://doi.org/10.1007/s40430-018-1232-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1232-3

Keywords

Search

Navigation