Skip to main content
SpringerLink
Log in

Interaction of magneto-nanoparticles in Williamson fluid flow over convective oscillatory moving surface

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

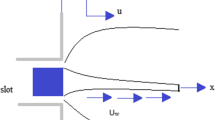
The paper addresses the problem of Williamson nanoliquid flow over an oscillatory stretching sheet. The effects of heat source/sink are initiated in the energy equation. The convective conditions at boundary are introduced to examine the mass and heat transport phenomenon. A set of appropriate variables are introduced to reduce number of independent variables in the governing equations. Analytic solutions by homotopic procedure are derived for coupled non-linear differential equations corresponding to non-Newtonian liquid. The interesting results of the problem are interpreted both from theoretical and practical aspects. The results indicate that heat transfer enhancement is possible with insertion of nanoparticles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  1. Sakiadis BC (1961) Boundary layer behavior on continuous solid surfaces: I boundary layer equations for two dimensional and axisymmetric flow. AIChE J 7:26–28

    Article  Google Scholar 

  2. Crane LJ (1970) Flow past a stretching plate. Z Angew Math Phy 21:645–647

    Article  Google Scholar 

  3. Anderson HI, Bech KH, Dandapat BS (1992) Magnetohydrodynamic flow of a power-law fluid over a stretching sheet. Int J Non Linear Mech 27:929–936

    Article  MATH  Google Scholar 

  4. Hassanien IA, Abdullah AA, Gorla RSR (1998) Flow and heat transfer in a power-law fluid over a non-isothermal stretching sheet. Math Comput Model 28:105–116

    Article  MATH  Google Scholar 

  5. Chen CH (2003) Heat transfer in a power-law fluid film over an unsteady stretching sheet. Heat Mass Transf 39:791–796

    Article  Google Scholar 

  6. Nadeem S, Haq RU, Lee C (2012) MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci Iran B 19:1550–1553

    Article  Google Scholar 

  7. Hsiao K (2017) Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl Therm Eng 112:1281–1288

    Article  Google Scholar 

  8. Williamson RV (1929) The flow of pseudoplastic materials. Ind Eng Chem Res 21:1108

    Article  Google Scholar 

  9. Nadeem S, Hussain ST, Lee C (2013) Flow of a Williamson fluid over a stretching sheet. Braz J Chem Eng 30:619–625

    Article  Google Scholar 

  10. Kumar KG, Rudraswamy NG, Gireesha BJ, Manjunatha S (2017) Non-linear thermal radiation effect on Williamson fluid with particle-liquid suspension past a stretching surface. Results Phys 7:3196–3202

    Article  Google Scholar 

  11. Hayat T, Saeed Y, Asad S, Alsaedi A (2015) Soret and Dufour effects in the flow of Williamson fluid over an unsteady stretching surface with thermal radiation. Z Naturforsch 70:235–243

    Google Scholar 

  12. Shateyi S, Motsa SS (2009) Thermal radiation effects on heat and mass transfer over an unsteady stretching surface. Math Probl Eng 2009:965603

    Article  MATH  Google Scholar 

  13. Ali M, Alim MA, Alam MS (2015) Similarity solution of heat and mass transfer flow over an inclined stretching sheet with viscous dissipation and constant heat flux in presence of magnetic field. Proc Eng 105:557–569

    Article  Google Scholar 

  14. Sheikholeslami M, Kataria HR, Mittal AS (2017) Radiation effects on heat transfer of three dimensional nanofluid flow considering thermal interfacial resistance and micro mixing in suspensions. Chin J Phys 55:2254–2272

    Article  MathSciNet  Google Scholar 

  15. Ali N, Khan SU, Sajid M, Abbas Z (2016) MHD flow and heat transfer of couple stress fluid over an oscillatory stretching sheet with heat source/sink in porous medium. Alex Eng J 55:915–924

    Article  Google Scholar 

  16. Mendu DSU (2014) Free convection in MHD micropolar fluid with radiation and chemical reaction effects. Chem Ind Chem Eng Q 20:183–195

    Article  Google Scholar 

  17. Mukhopadhyay S, Ranjan P, Layek GC (2013) Heat transfer characteristics for the Maxwell fluid flow past an unsteady stretching permeable surface embedded in a porous medium with thermal radiation. J Appl Mech Tech Phys 54:385–396

    Article  MATH  Google Scholar 

  18. Hayat T, Afzaal MF, Fetecau C, Hendi AA (2011) Slip effects on the oscillatory flow in a porous medium. J Porous Media 14:481493

    Google Scholar 

  19. Ishak A (2010) Thermal boundary layer flow over a stretching sheet in a micropolar fluid with radiation effect. Meccanica 45:367–373

    Article  MATH  Google Scholar 

  20. Patil PM, Kulkarni PS (2008) Effects of chemical reaction on free convective flow of a polar fluid through a porous medium in the presence of internal heat generation. Int J Therm Sci 47:1043–1054

    Article  Google Scholar 

  21. Choi S (1995) Enhancing thermal conductivity of fluids with nanoparticle. In: Development and applications of non-Newtonian flow, ASME, FED-vol 231/MD-vol 66, pp 99–105

  22. Mahian O, Kianifar A, Kalogirou SA, Pop I, Wongwises S (2013) A review of the applications of nanofluids in solar energy. Int J Heat Mass Transf 57:582

    Article  Google Scholar 

  23. Hsiao K (2016) Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl Therm Eng 98:850–861

    Article  Google Scholar 

  24. Si X, Li H, Zheng L, Shen Y, Zhang X (2017) A mixed convection flow and heat transfer of pseudo-plastic power law nanofluids past a stretching vertical plate. Int J Heat Mass Transf 105:350–358

    Article  Google Scholar 

  25. Hsiao K (2017) To promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-nanofluid with parameters control method. Energy 130:486–499

    Article  Google Scholar 

  26. Turkyilmazoglu M (2014) Nanofluid flow and heat transfer due to a rotating disk. Comput Fluids 94:139–146

    Article  MathSciNet  Google Scholar 

  27. Turkyilmazoglu M (2015) A note on the correspondence between certain nanofluid flows and standard fluid flows. J Heat Transfer Trans ASME 137:024501

    Article  Google Scholar 

  28. Sheikholeslami M, Shehzad SA (2017) Magnetohydrodynamic nanofluid convection in a porous enclosure considering heat flux boundary condition. Int J Heat Mass Transf 106:1261–1269

    Article  Google Scholar 

  29. Khan SU, Ali N, Abbas Z (2016) Influence of heat generation/absorption with convective heat and mass conditions in unsteady flow of Eyring Powell nanofluid over porous oscillatory stretching surface. J. Nanofluids 5:351–362

    Article  Google Scholar 

  30. Zhu J, Wang S, Zheng L, Zhang X (2017) Heat transfer of nanofluids considering nanoparticle migration and second-order slip velocity. Appl Math Mech 38:125–136

    Article  MathSciNet  Google Scholar 

  31. Sheikholeslami M, Rokni HB (2017) Influence of melting surface on MHD nanofluid flow by means of two phase model. Chin J Phys 55:1352–1360

    Article  Google Scholar 

  32. Sheikholeslami M, Sadoughi MK (2017) Mesoscopic method for MHD nanofluid flow inside a porous cavity considering various shapes of nanoparticles. Int J Heat Mass Transf 113:106–114

    Article  Google Scholar 

  33. Shehzad SA, Abdullah Z, Alsaedi A, Abbasi FM, Hayat T (2016) Thermally radiative three-dimensional flow of Jeffrey nanofluid with internal heat generation and magnetic field. J Magnet Magnet Mater 397:108–114

    Article  Google Scholar 

  34. Sheikholeslami M, Oztop HF (2017) MHD free convection of nanofluid in a cavity with sinusoidal walls by using CVFEM. Chin J Phys 55:2291–2304

    Article  Google Scholar 

  35. Sheikholeslami M, Shehzad SA (2018) Non-Darcy free convection of Fe3O4-water nanoliquid in a complex shaped enclosure under impact of uniform Lorentz force. Chin J Phys 56:270–281

    Article  Google Scholar 

  36. Lin Y, Zheng L, Zhang X, Ma L, Chen G (2015) MHD pseudo-plastic nanofluid unsteady flow and heat transfer in a finite thin film over stretching surface with internal heat generation. Int J Heat Mass Transf 84:903–911

    Article  Google Scholar 

  37. Zhang C, Zheng L, Zhang X, Chen G (2015) MHD flow and radiation heat transfer of nanofluids in porous media with λ variable surface heat flux and chemical reaction. Appl Math Model 39:165–181

    Article  MathSciNet  Google Scholar 

  38. Zheng L, Zhang C, Zhang X, Zhang J (2013) Flow and radiation heat transfer of a Nanofluid over a stretching sheet with velocity slip and temperature jump in porous medium. J Franklin Inst 350:990–1007

    Article  MathSciNet  MATH  Google Scholar 

  39. Hsiao K (2017) Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int J Heat Mass Transf 112:983–990

    Article  Google Scholar 

  40. Kousar N, Liao S (2011) Unsteady non-similarity boundary-layer flows caused by an impulsively stretching flat sheet. Nonlinear Anal Real World Appl 12:333–342

    Article  MathSciNet  MATH  Google Scholar 

  41. Rashidi MM, Mohimanian SAP, Abbasbandy S (2011) Analytic approximate solutions for heat transfer of a micropolar fluid through a porous medium with radiation. Commun Nonlinear Sci Numer Simul 16:1874–1889

    Article  Google Scholar 

  42. Han S, Zheng L, Li C, Zhang X (2014) Coupled flow and heat transfer in viscoelastic fluid with Cattaneo–Christov heat flux model. Appl Math Lett 38:87–93

    Article  MathSciNet  MATH  Google Scholar 

  43. Ali N, Khan SU, Abbas Z, Sajid M (2016) Soret and Dufour effects on hydromagnetic flow of viscoelastic fluid over porous oscillatory stretching sheet with thermal radiation. J Braz Soc Mech Sci Eng 38:2533–2546

    Article  Google Scholar 

  44. Turkyilmazoglu M (2012) Solution of the Thomas–Fermi equation with a convergent approach. Commun Nonlinear Sci Numer Simul 17:4097–4103

    Article  MathSciNet  MATH  Google Scholar 

  45. Turkyilmazoglu M (2017) Parametrized Adomian decomposition method with optimum convergence. Trans Model Comput Simul 24:21

    MathSciNet  Google Scholar 

  46. Turkyilmazoglu M (2018) Convergence accelerating in the homotopy analysis method: a new approach. Adv Appl Math Mech (in press)

  47. Zheng LC, Jin X, Zhang XX, Zhang JH (2013) Unsteady heat and mass transfer in MHD flow over an oscillatory stretching surface with Soret and Dufour effects. Acta Mech Sin 29:667–675

    Article  MathSciNet  MATH  Google Scholar 

  48. Abbas Z, Wang Y, Hayat T, Oberlack M (2008) Hydromagnetic flow in a viscoelastic fluid due to the oscillatory stretching surface. Int J Nonlinear Mech 43:783–797

    Article  MATH  Google Scholar 

  49. Turkyilmazoglu M (2013) The analytical solution of mixed convection heat transfer and fluid flow of a MHD viscoelastic fluid over a permeable stretching surface. Int J Mech Sci 77:263–268

    Article  Google Scholar 

  50. Hayat T, Mustafa M, Pop I (2010) Heat and mass transfer for Soret and Dufour’s effect on mixed convection boundary layer flow over a stretching vertical surface in a porous medium filled with a viscoelastic fluid. Commun Nonlinear Sci Numer Simul 15:1183–1196

    Article  MathSciNet  MATH  Google Scholar 

  51. Turkyilmazoglu M (2016) Determination of the correct range of physical parameters in the approximate analytical solutions of nonlinear equations using the Adomian decomposition method. Mediterr J Math 13:4019–4037

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We are thankful to the anonymous reviewers for their useful comments to improve the earlier version of the paper.

Funding

There are no funders to report for this submission.

Author information

Authors and Affiliations

  1. Department of Mathematics, COMSATS Institute of Information Technology, Sahiwal, 57000, Pakistan

    Sami Ullah Khan & S. A. Shehzad

  2. Department of Mathematics and Statistics, International Islamic University, Islamabad, 44000, Pakistan

    N. Ali

Authors
  1. Sami Ullah Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. A. Shehzad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. N. Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. A. Shehzad.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Technical Editor: Cezar Negrao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khan, S.U., Shehzad, S.A. & Ali, N. Interaction of magneto-nanoparticles in Williamson fluid flow over convective oscillatory moving surface. J Braz. Soc. Mech. Sci. Eng. 40, 195 (2018). https://doi.org/10.1007/s40430-018-1126-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1126-4

Keywords

Search

Navigation